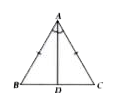
In a ΔABC,∠B>∠C.If AD⊥BCandAE is the bisector of ∠BAC then prove that ∠DAE=12(∠B−∠C).

Text Solution
Since AE is the bisector of ∠BAC, we have
∠BAE=∠CAE ....(i)
In ΔABD we have ∠ADB=90∘
∴∠ABD+∠BAD=90∘
⇒∠ABD=(90∘−∠BAD)
⇒∠B=(90∘−∠BAD). ....(ii)
In ΔADC we have ∠ADC=90∘
∴∠CAD+∠ACD=90∘
⇒∠ACE=(90∘−∠CAD)
⇒∠C=(90∘−∠CAD). ....(iii)
On subtracting (iii) from (ii), we get
(∠B−∠C)=(90∘−∠BAD)−(90∘−∠CAD)
=∠CAD−∠BAD
=(∠CAE+∠DAE)−(∠BAE−∠DAE)
=2∠DAE [using (i)].
∴∠DAE=12(∠B−∠C).
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 8
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
In ΔABC, if ∠C>∠B, then
ABC>ACBAB>ACCAB<ACDBC<ACIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
A36∘B72∘C108∘D144∘
In the given figure, AD is altitude and AE is bisector of angle BAC of ΔABC. Show that ΔDAE=12(∠B−∠C)

View SolutionIn a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionIn △ABC,∠A=40∘ if bisector of ∠B and ∠C meets at O then prove that ∠BOC=110∘
View SolutionIn a ΔABC,∠C=3∠B=2(∠A+∠B) find the three angles.
View Solution