In a right triangle,Prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse
Given In ΔABC,∠B=90∘ and D is the mid-point of AC
Construction produce BD to E such that BD =DE and join EC
To Prove
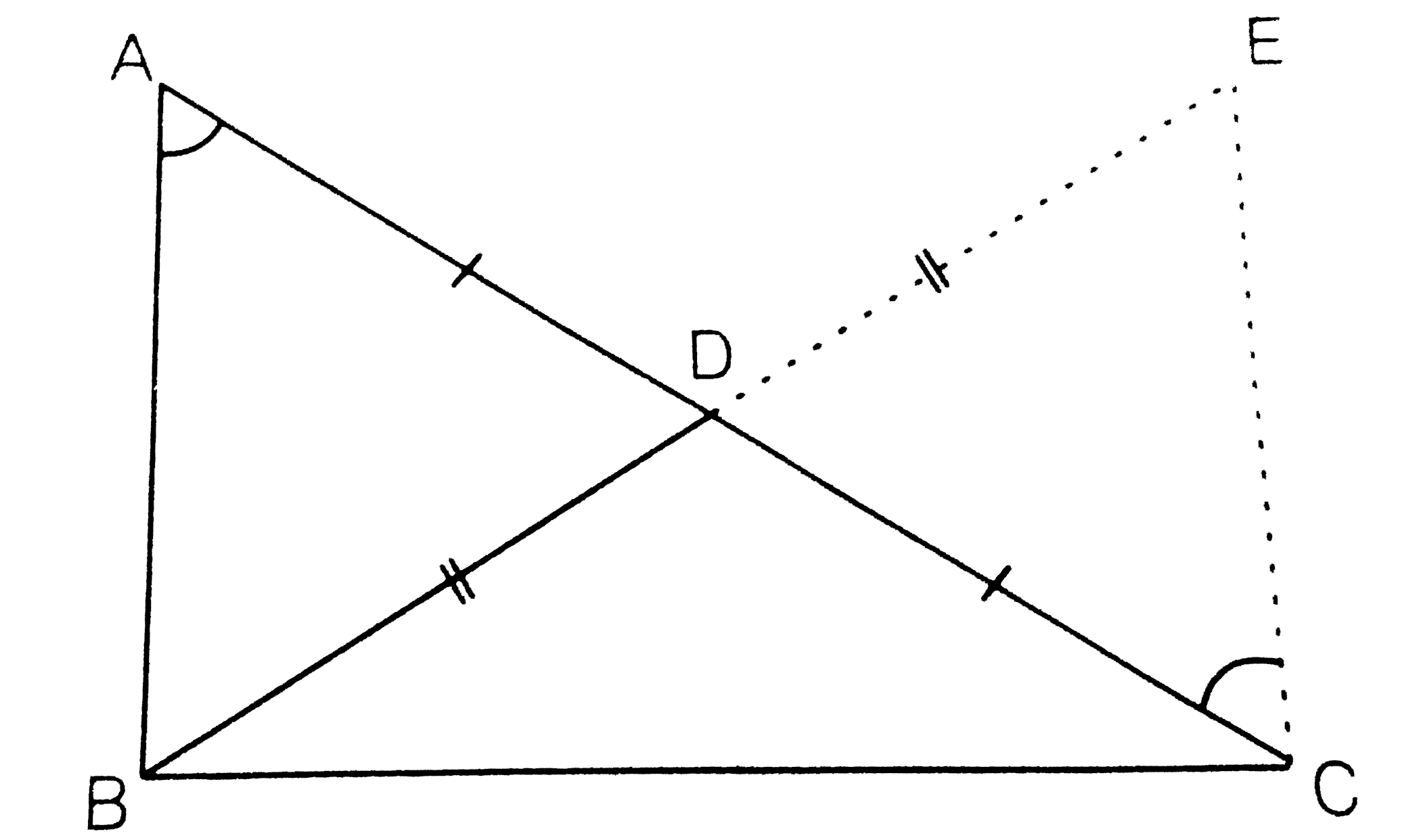
Proof In ΔADBandΔCDE AD=DC [∵D is mid-point ofAC]
BD =DE [by construction ]
and ∠ADB=∠CDE [vertically opposite angles ]
∴ΔADB≅ΔCDE [by SAS Congruence rule]
⇒AB=EC [by CPCT]
But ∠BADand∠DCE are alternate angles
So EC|| AB and BC is a transversal
∴∠ABC+∠BCE=180∘ [cointerior angles ]
⇒90∘+∠BCE=180∘ [∵∠ABC=90∘ given ]
⇒∠BCE=180∘−90∘
⇒∠BCE=90∘
In ΔABCandΔECB AB=EC [proved above]
BC=CB [common side]
and ∠ABC=∠ECB [each 90∘]
∴ΔABC≅ΔECB [by SAS congruence rule ]
⇒ AC=EB [by CPCT ]
⇒12EB=12AC [dividing both sides by 2]
⇒BD=12AC
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS11videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half of the hypotenuse.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionProve that every line segment has one and only one mid-point.
View Solution


