In a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BDC=2∠POC
Step by step video & image solution for In a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that: angleBDC= 2 anglePOC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(C )
28 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 3 MARKS QUESTIONS
5 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B) (true/false)
10 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
In a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BOP=3∠COP
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠POC=(2212)∘
View SolutionIn a square ABCD, diagonals meet at O. P is point on BC such that OB = BP.Show that (i) ∠POC=(2212)∘
(ii) ∠BDC=2∠POC
(iii) ∠BOP=3∠COP
View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View SolutionIn a square ABCD, show that AC2=2AB2.
View SolutionIn a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View SolutionABC is an equilateral triangle, P is a point in BC such that BP : PC =2 : 1.
Prove that : 9AP2=7AB2
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2
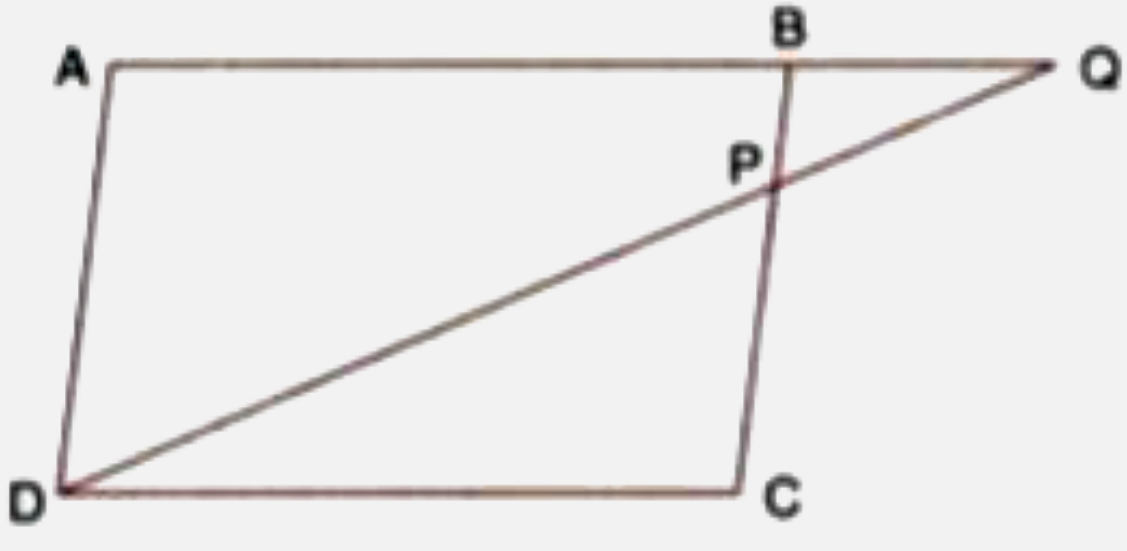
Calculate :
area of parallelogram ABCD.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2

Calculate :
area of triangle CDP.
View SolutionABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP : area of trapezium APCD = 1:5. Find the length of CP.
View Solution
