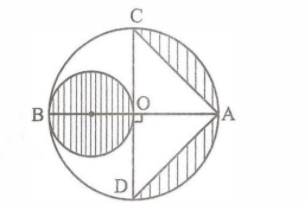
In Figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region.
To find the area of the shaded region between two circles, we will follow these steps:
Step 1: Identify the radius of the larger circle
Given that OA=7cm, and since OA is the radius of the larger circle, we have:
R=OA=7cm
Step 2: Calculate the radius of the smaller circle
The diameter OD of the smaller circle is equal to the radius of the larger circle divided by 2:
r=R2=72=3.5cm
Step 3: Calculate the area of the larger circle
The area A of a circle is given by the formula:
A=πR2
Substituting the value of R:
Alarger=π(7)2=π×49
Using π≈227:
Alarger=227×49=154cm2
Step 4: Calculate the area of the smaller circle
Using the same area formula for the smaller circle:
Asmaller=πr2=π(3.5)2=π×12.25
Again using π≈227:
Asmaller=227×12.25=38.5cm2
Step 5: Calculate the area of the shaded region
The area of the shaded region is the difference between the area of the larger circle and the area of the smaller circle:
Ashaded=Alarger−Asmaller=154−38.5=115.5cm2
Final Answer
The area of the shaded region is:
115.5cm2
Given that OA=7cm, and since OA is the radius of the larger circle, we have:
R=OA=7cm
The diameter OD of the smaller circle is equal to the radius of the larger circle divided by 2:
r=R2=72=3.5cm
The area A of a circle is given by the formula:
A=πR2
Substituting the value of R:
Alarger=π(7)2=π×49
Using π≈227:
Alarger=227×49=154cm2
Using the same area formula for the smaller circle:
Asmaller=πr2=π(3.5)2=π×12.25
Again using π≈227:
Asmaller=227×12.25=38.5cm2
The area of the shaded region is the difference between the area of the larger circle and the area of the smaller circle:
Ashaded=Alarger−Asmaller=154−38.5=115.5cm2
The area of the shaded region is:
115.5cm2
Topper's Solved these Questions
Similar Questions
In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
 View Solution
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
 View Solution
View SolutionIn Figure -4 AB, and CD are two diameters of a circle with centre O perpendiclualr to each other and OD is the diameter of the circle . If OA = 7 cm , then find the carea of the shaded region .
 View Solution
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Figure, two circles with centres A and B touch each other at the point C . If AC=8 cm and AB=3 cm , find the area of the shaded region.
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD.
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)
 View Solution
View Solution

