In Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
To prove that the lengths of the common tangents PQ and RS are equal, we will use the properties of triangles formed by the tangents and the radii of the circles.
1. Identify the Elements:
- Let O be the center of the larger circle and B be the center of the smaller circle.
- The points P and Q are points of tangency on the larger circle, while R and S are points of tangency on the smaller circle.
2. Consider Triangles △POA and △ROA:
- In triangle POA:
- OP is the radius of the larger circle.
- OA is the distance from the center O to the point A where the tangents intersect.
- In triangle ROA:
- OR is the radius of the smaller circle.
- OA is the same distance as in triangle POA.
3. Establish Equalities:
- Since OP=OR (both are radii of their respective circles),
- The angles ∠OPA and ∠ORA are both right angles (90 degrees) because the radius is perpendicular to the tangent at the point of tangency.
- The segment OA is common to both triangles.
4. Apply the Criteria for Similarity:
- By the criteria of similarity (AA criterion), we can conclude:
△POA∼△ROA
- From the similarity of triangles, we have:
PARA=OPOR(which is 1, since they are equal)
- Therefore, PA=RA.
5. Consider Triangles △QBA and △SBA:
- Similarly, for triangles QBA and SBA:
- BQ=BS (both are radii of their respective circles),
- ∠BQA=∠BSA (both are right angles),
- BA is common.
6. Apply the Criteria for Similarity Again:
- Thus, we have:
△QBA∼△SBA
- From this similarity, we conclude:
QA=SA
7. Relate the Lengths of the Tangents:
- Now we can express the lengths of the tangents:
PQ=PA+QAandRS=RA+SA
- Since PA=RA and QA=SA, we can substitute:
PQ=RS
8. Conclusion:
- Therefore, we have proved that the lengths of the common tangents are equal:
PQ=RS
- Let O be the center of the larger circle and B be the center of the smaller circle.
- The points P and Q are points of tangency on the larger circle, while R and S are points of tangency on the smaller circle.
- In triangle POA:
- OP is the radius of the larger circle.
- OA is the distance from the center O to the point A where the tangents intersect.
- In triangle ROA:
- OR is the radius of the smaller circle.
- OA is the same distance as in triangle POA.
- Since OP=OR (both are radii of their respective circles),
- The angles ∠OPA and ∠ORA are both right angles (90 degrees) because the radius is perpendicular to the tangent at the point of tangency.
- The segment OA is common to both triangles.
- By the criteria of similarity (AA criterion), we can conclude:
△POA∼△ROA
- From the similarity of triangles, we have:
PARA=OPOR(which is 1, since they are equal)
- Therefore, PA=RA.
- Similarly, for triangles QBA and SBA:
- BQ=BS (both are radii of their respective circles),
- ∠BQA=∠BSA (both are right angles),
- BA is common.
- Thus, we have:
△QBA∼△SBA
- From this similarity, we conclude:
QA=SA
- Now we can express the lengths of the tangents:
PQ=PA+QAandRS=RA+SA
- Since PA=RA and QA=SA, we can substitute:
PQ=RS
- Therefore, we have proved that the lengths of the common tangents are equal:
PQ=RS
Topper's Solved these Questions
Similar Questions
In Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
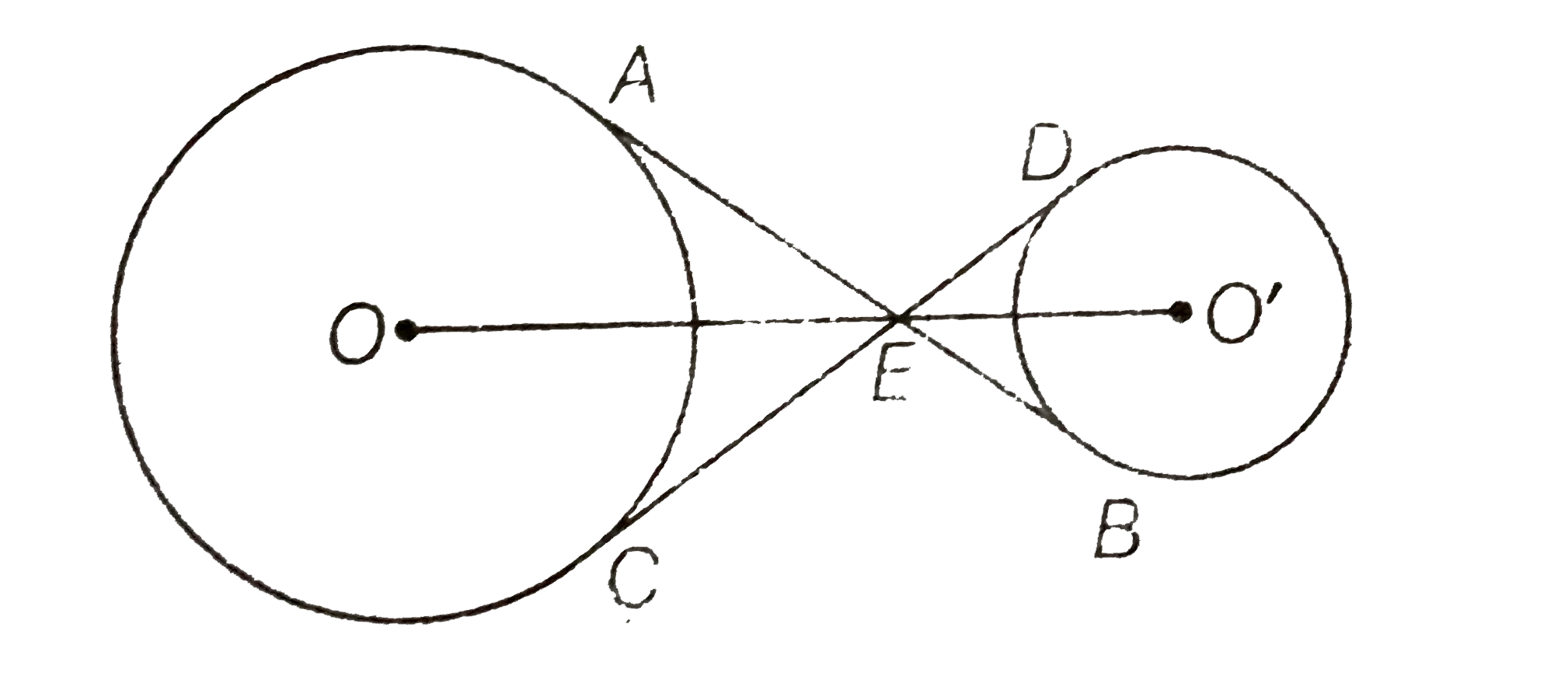 View Solution
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD
 View Solution
View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.
 View Solution
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
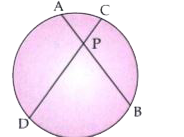 View Solution
View SolutionIn Fig. 10.62, PO⊥QO . The tangents to the circle at P and Q intersect at a point T . Prove that PQ and OT are right bisectors of each other. (FIGURE)
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View Solution

