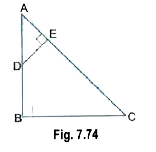
In figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

Given,
△ABE≅△ACD
Hence, AB=AC by CPCT. .....(1)
[CPTC: corresponding parts of congruent triangles]
and AE=AD by CPCT.
⇒AD=AE .....(2)
Dividing (2) by (1)
ADAB=AEAC ....(3)
In △ADE and △ABC
∠A=∠A (common angle)
ADAB=AEAC
from (3)
∴△ADE is similar to △ABC by SAS criterion.
Hence proved.
Topper's Solved these Questions
Similar Questions
Δ ABC and Δ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true? ΔABC≅ΔABD ΔABC≅ΔADB ΔABC≅ΔBAD
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ
 View Solution
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
 View Solution
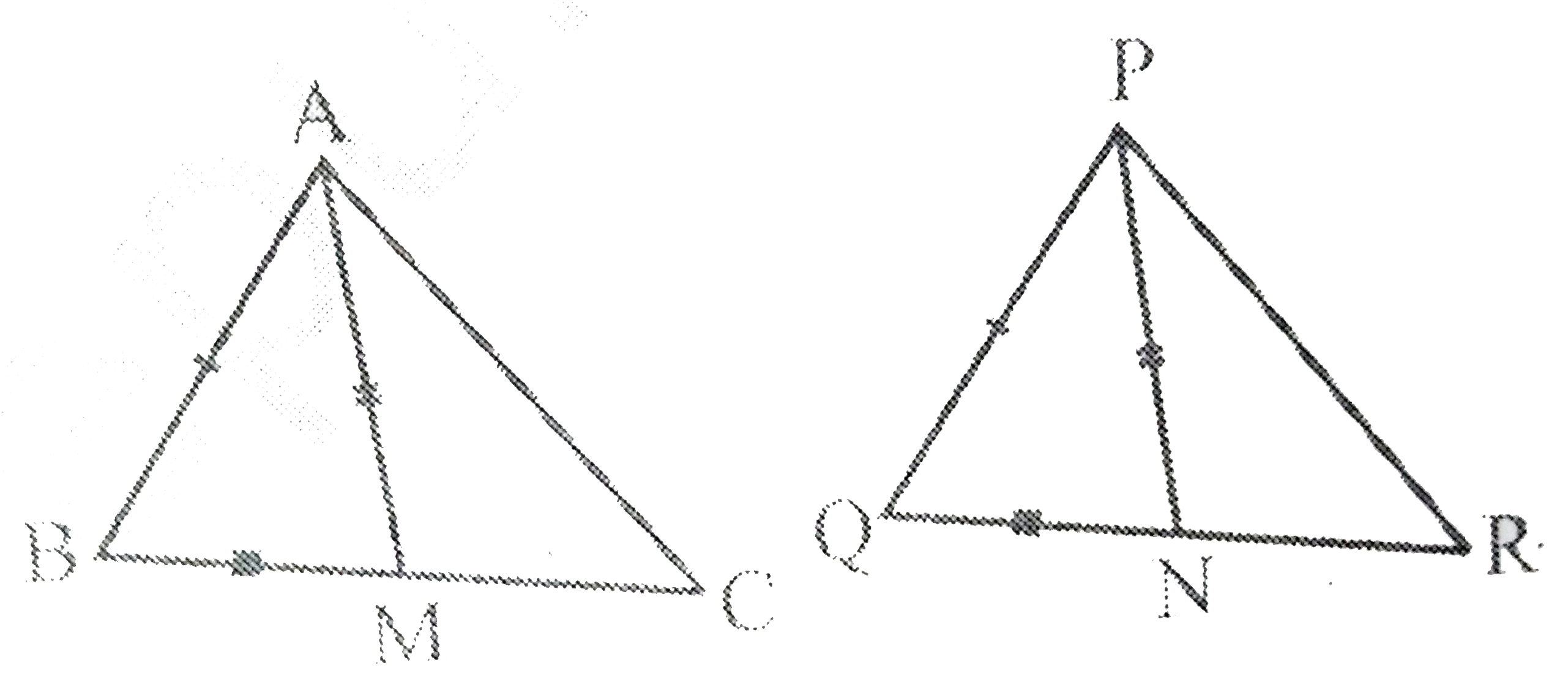
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
View SolutionAB⊥BC and DE⊥AC. Prove that ΔABC~ΔAED.
 View Solution
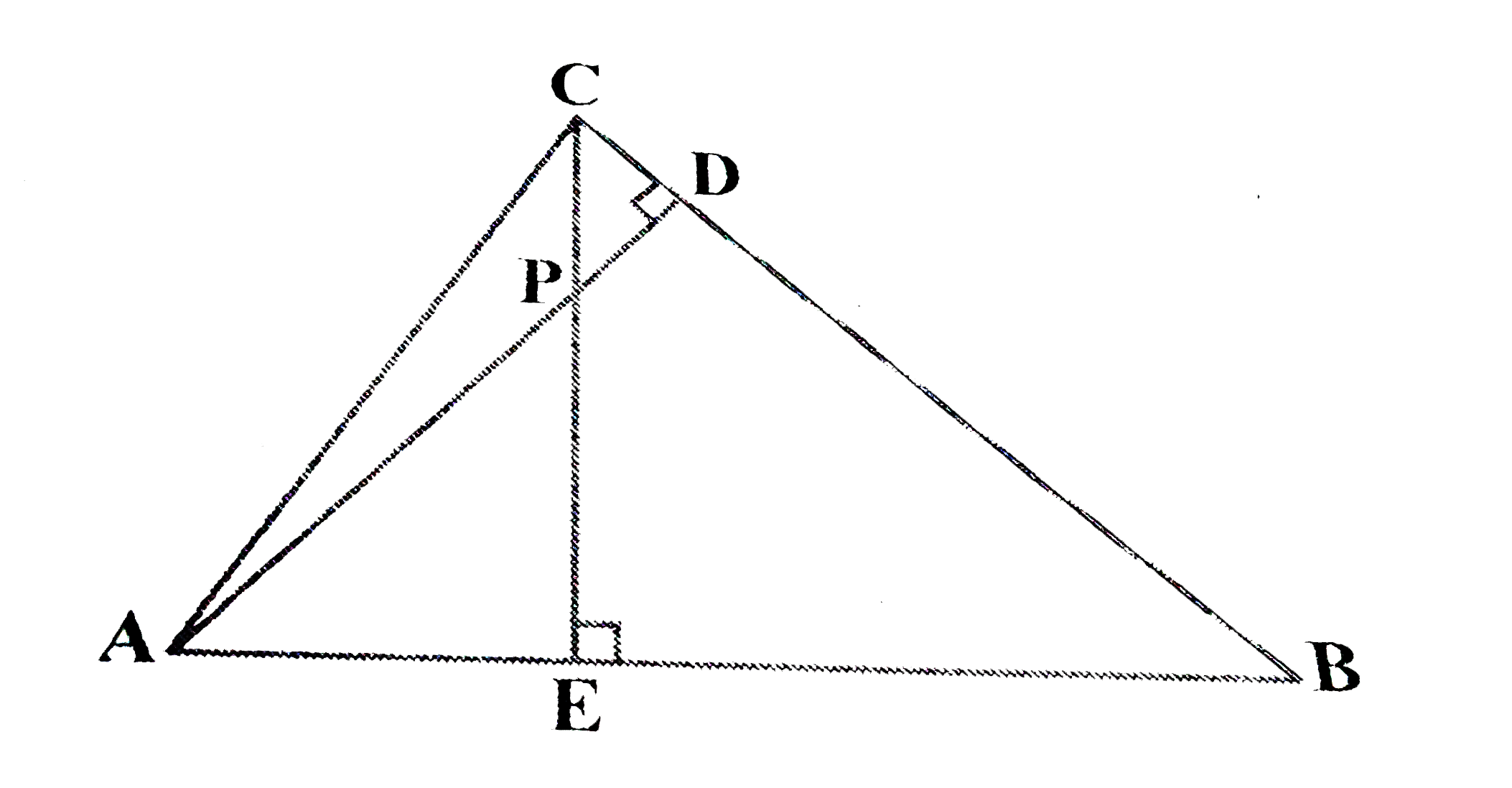
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
 View Solution
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
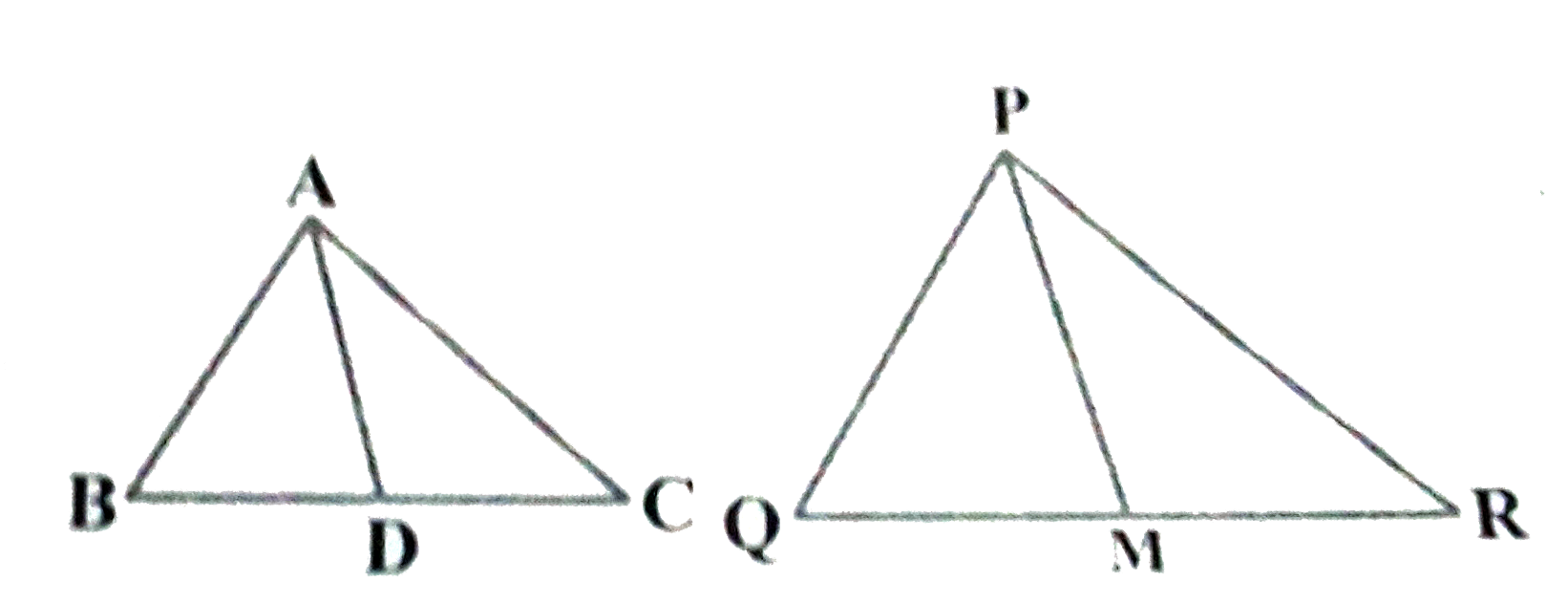 View Solution
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment AX⊥DEmeets BCat Y. Show that:(i) ΔMBC≅ΔABD(ii) a r\ (B Y X D)\ =\ 2\
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View Solution

