In figure QRQS=QTPRand ∠1=∠2. Show that ΔPQS~ΔTQR.

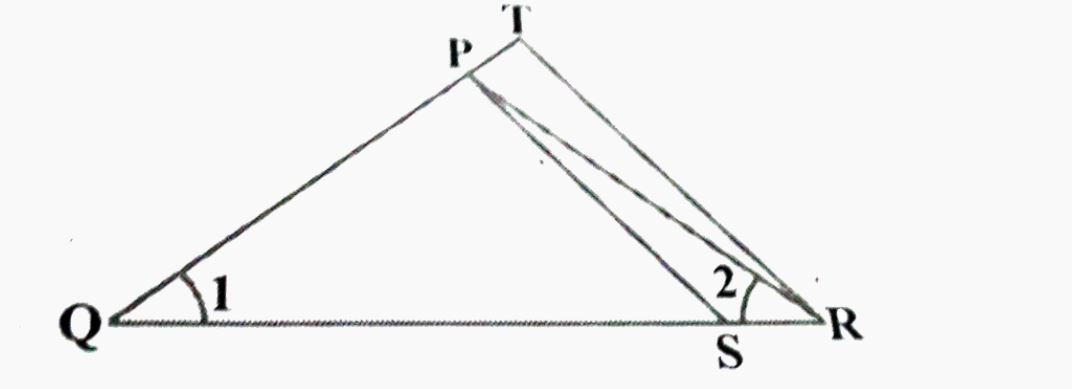
In △PQR,
Since, ∠1=∠2
∴ PR=PQ (Opposite sides of equal angles are equal) .....(1)
In △PQS and △TQR,
QRQS=QTPR
(Given)
i.e.,
QRQS=QTPR
....(From1)
Also, ∠Q is common
∴ By SAS criterion of similarity,
△PQS∼△TQR.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
What should come next in the following letter series ?
P Q P Q R P Q R S P Q R S T P Q R S T L P Q R S T U V P Q R S TASBUCQDR
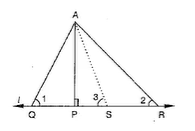
In figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
 View Solution
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
 View Solution
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
 View Solution
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
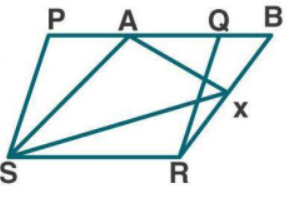
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
 View Solution
View Solution


