In the adjoining figure, AC is the diameter of a circle with centre O and chord BD⊥AC , intersecting each other at E. Find out the values of p,q,r in terms of x.

(i) Arc AD subtends ∠AOD at the centre and ∠ABD at a point B on the remaining part of the circle.
Now,∠AEB=90∘=x∘2.
Now, ∠AEB=90∘[∵BD⊥AC].
From ΔAEB,we get
p∘=180∘−(∠ABE+∠AEB)
⇒p∘=180∘−(∠ABD+∠AEB)=180∘−(x2+90∘)=(90∘−x∘2)
∴p=90−x2.
(ii) Arc AD subtends ∠AOD at the centre and ∠ACD at a point C of the circle.
∴∠ACD=12∠AOD=x∘2⇒q=x2
(iii) ∠ABC=90∘[ angle in a semicircle ]
⇒∠ABE+∠CBE=90∘⇒∠ABD+∠CBE=90∘
⇒x∘2+∠CBE=90∘⇒∠CBE=(90∘−x∘2)
⇒r=[90−x2].
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
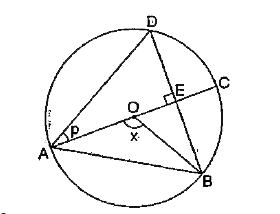 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−xIn the adjoining figure BD is the diameter of the circle and ∠BCA=41∘. Find ∠ABD:
 A41∘B49∘C22.5∘D20.5∘
A41∘B49∘C22.5∘D20.5∘
In the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.

View SolutionIn the adjoining figure, AC is the diameter of the circle. If ∠BDC=115∘, then find the value of ∠ACB.
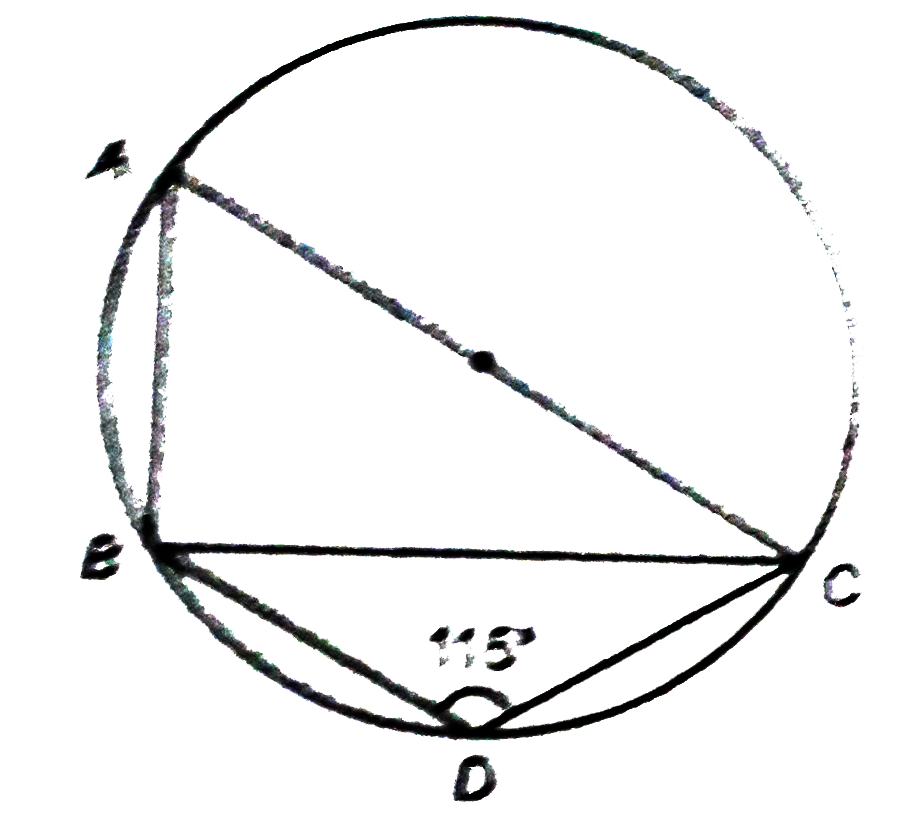
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the adjoining figure, AOB is the diameter and O is the centre of the circle. If ∠BDC=60∘, then find the value of ∠ABC.

View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
View Solution