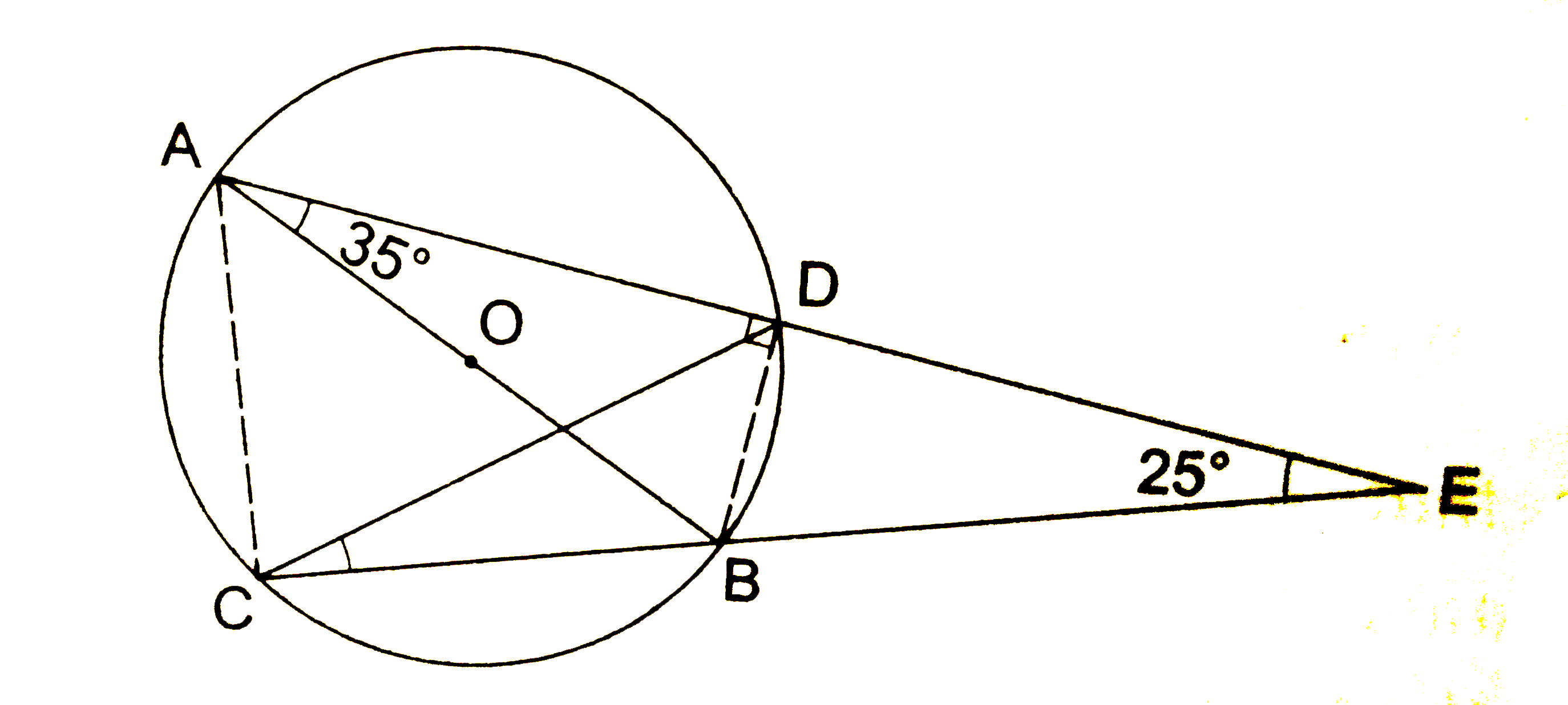
In the given figure, AB is a diameter of a circle with centre O. If ADE and CBE are straight lines, meeting at E such that ∠BAD=35∘ and ∠BED=25∘ , find (i) ∠DBC,(ii)∠BCD and (ii) ∠CDB.
Video Solution
Text Solution
Join AC and BD.
Now, ∠ADB=90∘ ( angle in a semicircle ) .
Since ADE is a straight line, we have
∠ADB+∠EDB=180∘⇒90∘+∠EDB=180∘⇒∠EDB=180∘−90∘=90∘
In ΔDBE, we have
∠DBE+∠BED+∠EDB=180∘
⇒∠DBE+25∘+90∘=180∘
⇒∠DBE=180∘−115∘=65∘.
(i) Since CBE is a straight line, we have
∠DBE+∠DBE=180∘⇒∠DBC+65∘=180∘⇒∠DBC=180∘−65∘=115∘
(ii) ∠BCD=∠BAD=35∘ [ angles in the same segment] .
(iii) In ΔDBC , we have
∠DBC+∠BCD+∠CDB=180∘
⇒115∘+35∘+∠CDB=180∘
⇒∠CDB=(180∘−150∘)=30∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
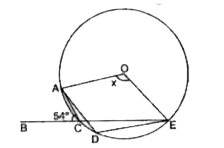
In the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
 A126∘B54∘C108∘D90∘
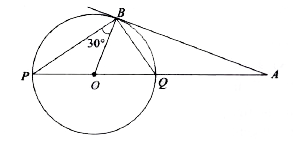
A126∘B54∘C108∘D90∘In the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1
In the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘, find ∠AOC
View SolutionIn the given fig, AB is the diameter of the circle with centre O. The point C, D and E are on the circle such that AC = CD = DE = EB. Find ∠EBA.
View Solution