In the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
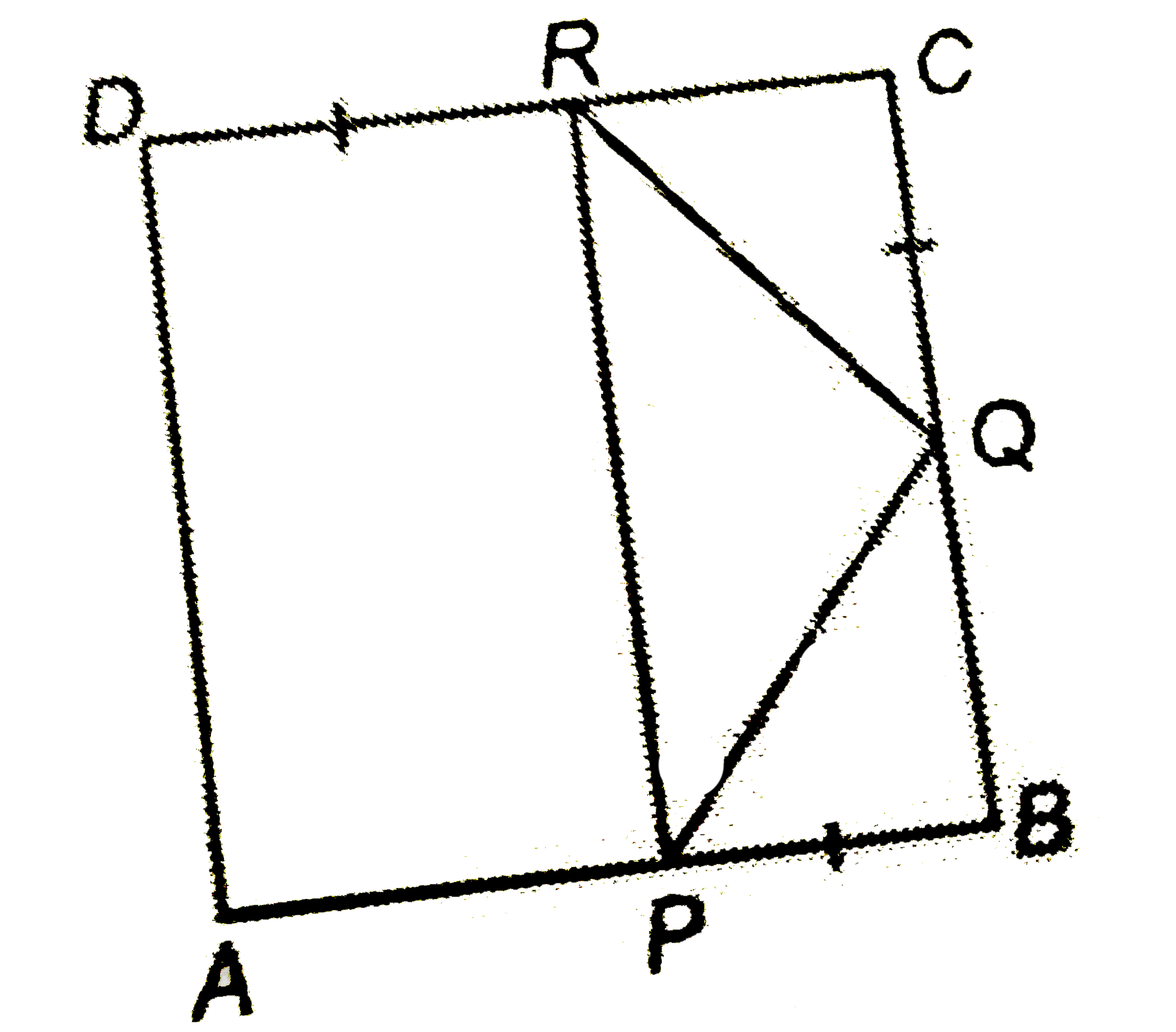
Step by step video, text & image solution for In the given figure, ABCD is a square and anglePQR=90^(@).If PB=QC=DR, prove that. (i) QB = RC (ii) PQ = QR (iii) angleQPR=45^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)10videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
In the given figure, DEFG is a square and ∠BAC=90∘, Prove that
(i)ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii)DE2=BD×EC
 View Solution
View SolutionIn the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
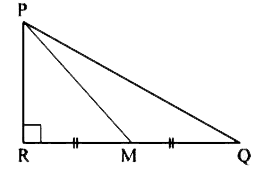
View SolutionIn the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
 View Solution
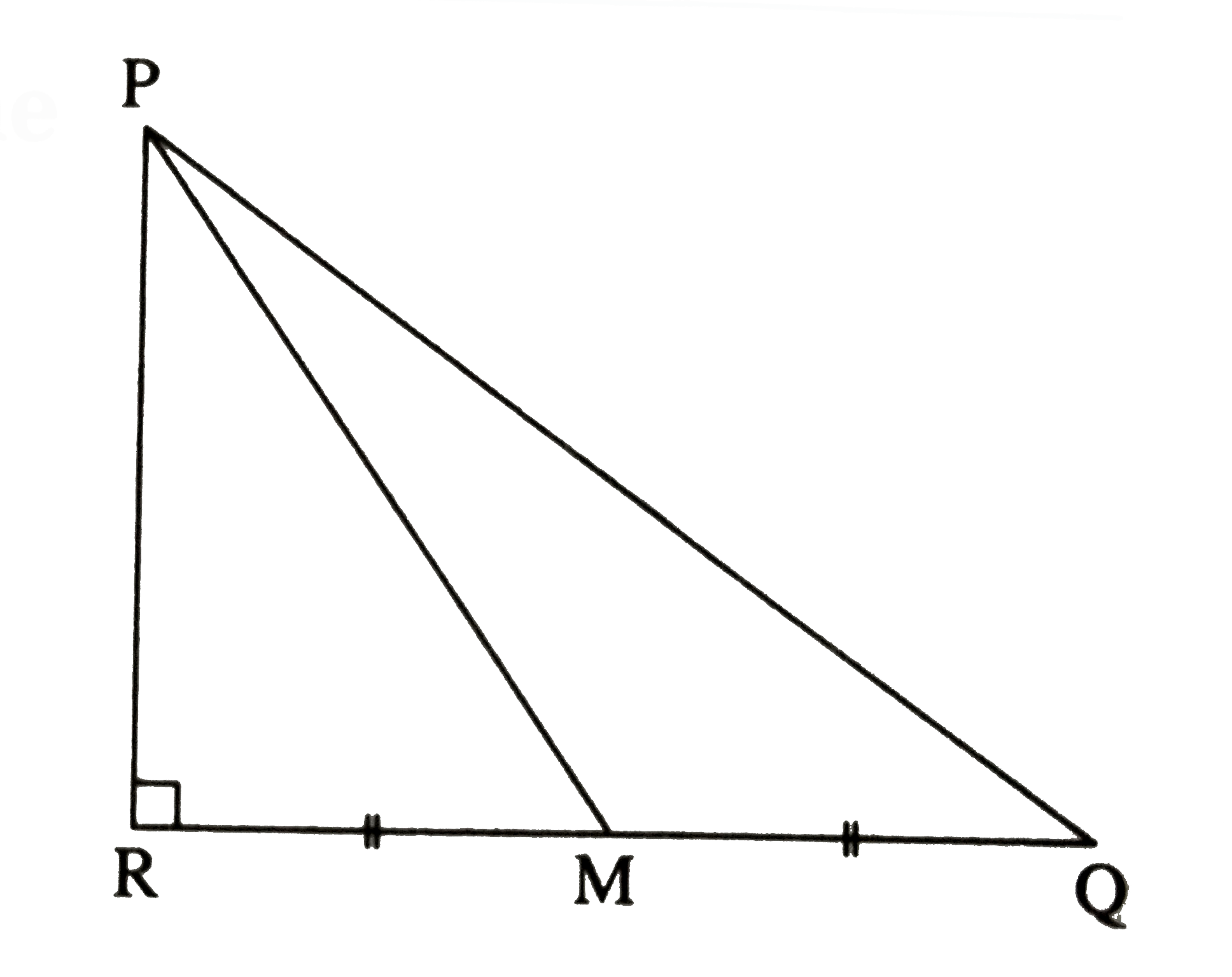
View SolutionIn the figure , M is the midpoint of QR .
∠PRQ=90∘.
Prove that ,
PQ2=4PM2−3PR2 .
 View Solution
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.
 View Solution
View SolutionIn the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.
 View Solution
View SolutionIn the given figure, ABCD is a square and P is a point inside it such that PB=PD. Prove that CPA is a straight line.
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
 View Solution
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
 View Solution
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.
 View Solution
View Solution

