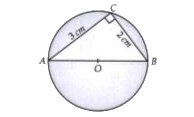
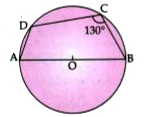
In the given figure, AC is a diameter of a circle with centre O. If CD∣∣BE,∠AOB=80∘ and ∠ACE=10∘ , find.
(i)∠BEC,(ii)∠BCD and (ii)∠CED

Text Solution
(i) Since AOC is a straight line, we have
∠AOB+∠BOC=180∘
⇒80∘+∠BOC=180∘
⇒∠BOC=180∘−80∘=100∘
Now , arc BC makes ∠BOC=100∘ at the centre and ∠BEC at a point E on the remaining part of circle.
∴∠BEC=12∠BOC=(12×100∘)=50∘
(ii) Arc AB makes ∠AOB at the centreand ∠ACB at a point on the remaining part of the circle.
∴∠ACB=12∠AOB=(12×80∘)=40∘
Now, CD∣∣CD and CE is the transversal.
∴∠ECD=∠BEC=50∘[ alt. int. ∠s ]
∴∠BCD=∠ACB+∠ACE+∠ECD
=40∘+10∘+50∘=100∘
(iii) DEBC is acyclic quadrilateral.
∴∠BED+∠BCD=180∘
⇒∠BEC+∠CED+∠BCD=180∘
⇒50∘+∠CED+100∘=180∘
⇒∠CED=180∘−150∘=30∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
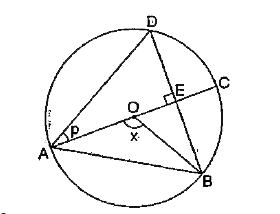 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−xIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,AC=d,andCD=l, then l is equal to
 Ad√3Bd/√3C3dD√3d/2
Ad√3Bd/√3C3dD√3d/2In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘
In the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
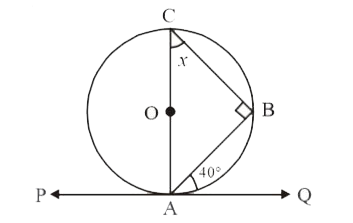
View SolutionIn the given Fig., AC is diameter of the circle with centre O and A is point of contact, then find x.
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to
View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to

View Solution