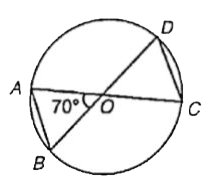
In the given figure, O is the centre of a circle. IF ∠AOD=140∘ and ∠CAB=50∘, calculate.
(I)∠EDB,(ii)∠FBD.

Video Solution
Text Solution
The correct Answer is:(i)∠EDB=50∘,(ii)∠EBD=110∘
∠BOD=180∘−∠AOD=180∘−140∘=40∘
OB=OD⇒∠OBD=∠ODB=70∘
∠CAB+∠BDC=180∘[∵ ABDC is a cyclic ]
⇒∠CAB+∠ODB+∠ODC=180∘
⇒50∘+70∘+∠ODC=180∘
⇒∠ODC=60∘
∴∠EDB=180∘−(60∘+70∘)=50∘
and ∠EBD=180∘−∠OBD=180∘−70∘=110∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘In the given figure, O is the centre of the circle. The value of x is
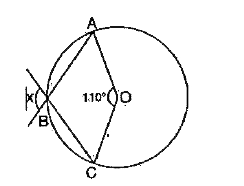 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
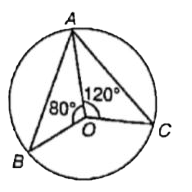 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the above
In the given figure,O is the centre of the circle ∠OAB=30∘ and ∠OCB=40∘. Calculate ∠AOC
View SolutionIn the given figure, if O is centre of circle, then ∠PQR=
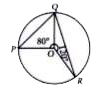
View SolutionIn the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
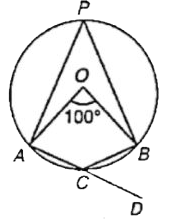
View SolutionIn the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
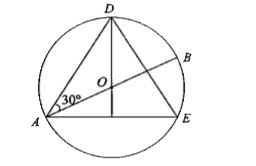
View SolutionIn the given figure, O is the centre of the circle. Then ∠AED measure
View Solution
