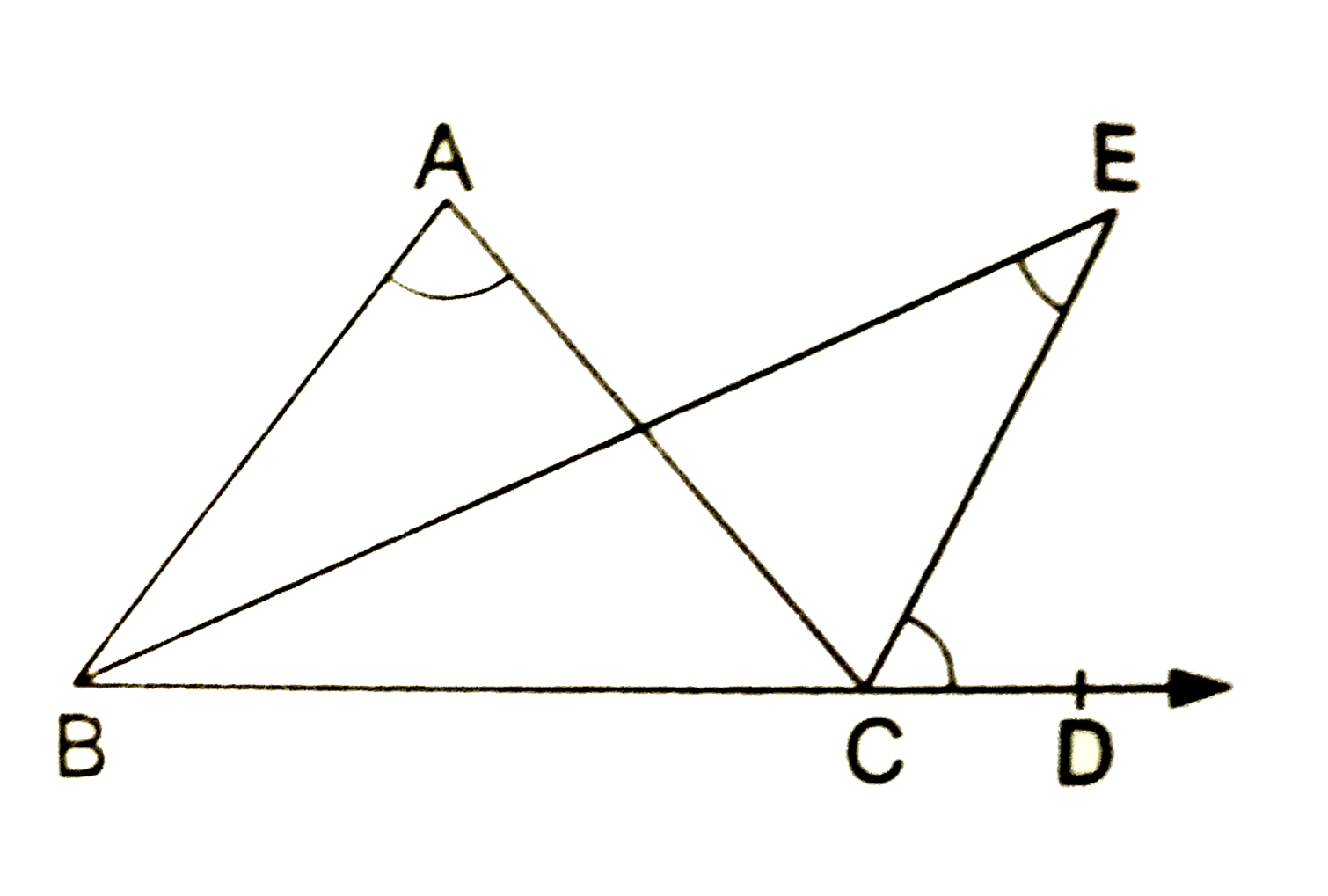
In the given figure, the side BC of ΔABC has been produced to a point D. If the bisectors of ∠ABCand∠ACD meet at point E then prove that ∠BEC=12∠BAC.
Text Solution
Side BC of ΔABC has been produced to D.
∴∠ACD=∠BAC+∠ABC
⇒12∠ACD=12∠BAC+12∠ABC
⇒∠ECD=12∠BAC+12∠ABC. ....(i)
Again, side BC of ΔEBC has been produced to D.
∴∠ECD=∠CBE+∠BEC
⇒∠ECD=12∠ABC+∠BEC. (ii)
From (i) and (ii), we get
12∠ABC+∠BEC=12∠BAC+12∠ABC
[each equal to ∠ECD].
∴∠BEC=12∠BAC.
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 8
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
If ΔABC,∠A=52∘, Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBDand∠BCE meet at point O, then ∠BOC is equal to:
A106∘B64∘C16∘D32∘In △ABC ,∠B=72∘ and,∠C=44∘. Side BC is produced to D. The bisectors of ∠B and ∠ACD meet at E. What is the measure of ∠BEC
त्रिभुज ABC में,∠B=72∘ तथा ∠C=44∘ है | भुजा BC को D तक बढ़ाया जाता है | ∠B तथा ∠ACD के समद्विभाजक Eपर मिलते हैं | कोण BEC का मान क्या होगा ?A36∘B32∘C46∘D58∘The side BC of ΔABC is produced to D. If ∠ACD=114∘ and ∠ABC=(12)∠BAC, what is the value (in degrees) of ∠BAC?
A36B48C76D84
In ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIn ΔABC exterior angle bisectors of ∠Band∠C meets at point P if ∠BAC=80∘ then find ∠BPC.
View SolutionThe side BC of ΔABC is product to N. bisector of angle meets BC at M. Prove that ∠ABC+∠ACN=2∠AMC
View SolutionThe side BC of ΔABC is product to N. bisector of angle meets BC at M. Prove that ∠ABC+∠ACN=2∠AMC
View Solution
