Let f(x)=xsinπx, x>0 . Then for all natural numbers n, f′(x) vanishes at A unique point in the interval (n, n+12) a unique point in the interval (n+12, n+1) a unique point in the interval (n, n+1) two points in the interval (n, n+1)
We have f'(x)=sinπx+πxcosπx=0
⇒ tanπx=−πx
Now we draw the graphs of y=tanπx and y=−πx and look for their points of intersection. y=tanπx has period 1.
Graphs are as shown in the following figure.
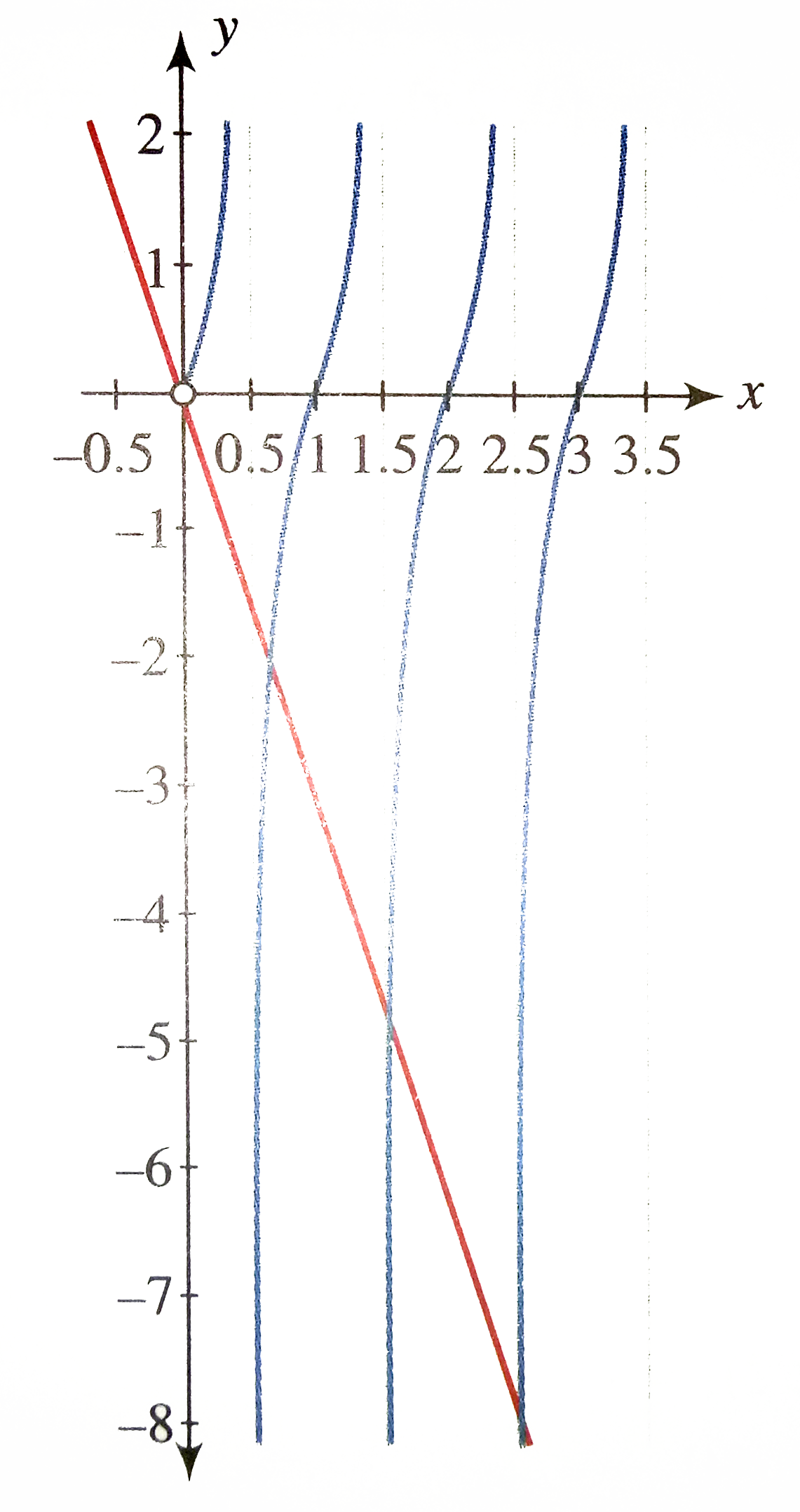
⇒ x∈(n+12,n+1)or(n,n+1)
Hence (b) and (c) are correct options.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Let f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at (A)a unique point in the interval (n,n+12) (B)a unique point in the interval (n+12,n+1) (C)a unique point in the interval (n,n+1) (D)two points in the interval (n,n+1)
View SolutionThe number of natural numbers n lying in the interval [2, 2000] such that hcf(n,36)=1, is __________
View Solution
Knowledge Check
Let xn=(2n+3n)1/2n for all natural number n.
ThenAlimn→∞xn=∞Blimn→∞xn=√3Climn→∞xn=√3+√2Dlimn→∞xn=√5Suppose the function f(x)=xn,n≠0 is differentiable for all x. then n can be any element of the interval
A[1,∞)B(0,∞)C(1/2,∞)Dnone of the aboveLet n be a natural and let 'a' be a real number. The number of zeros of x2n+1−(2n+1)x+a=0 in the interval [−1,1] is -
A2 if a gt 0B2 if a lt 0CAt most one for every value of aDAt least three for every value of a
Let A = {0,1} and N the set of all natural numbers. Then the mapping f:N→A defined by f (2n-1)=0, f (2n) =1 ∀n∈N is many-one onto.
A. True B. False
View SolutionGiven the function f(x)=x3 on the interval [-2,3] , find the lower (sn) and the upper (Sn) integral sums for the given interval by subdividing it into n equal parts.
View SolutionIf f(x)=1+xm(x−1)n,m,n∈N, then f'(x)=0 has atleast one root in the interval
View Solutionthe intersection of all the intervals having the form [1+1n,6,−2n], where is a postive integer is
View SolutionSuppose the function f(x)=xn,n≠0 is differentiable for all x. Then n can be any element of the interval
View Solution