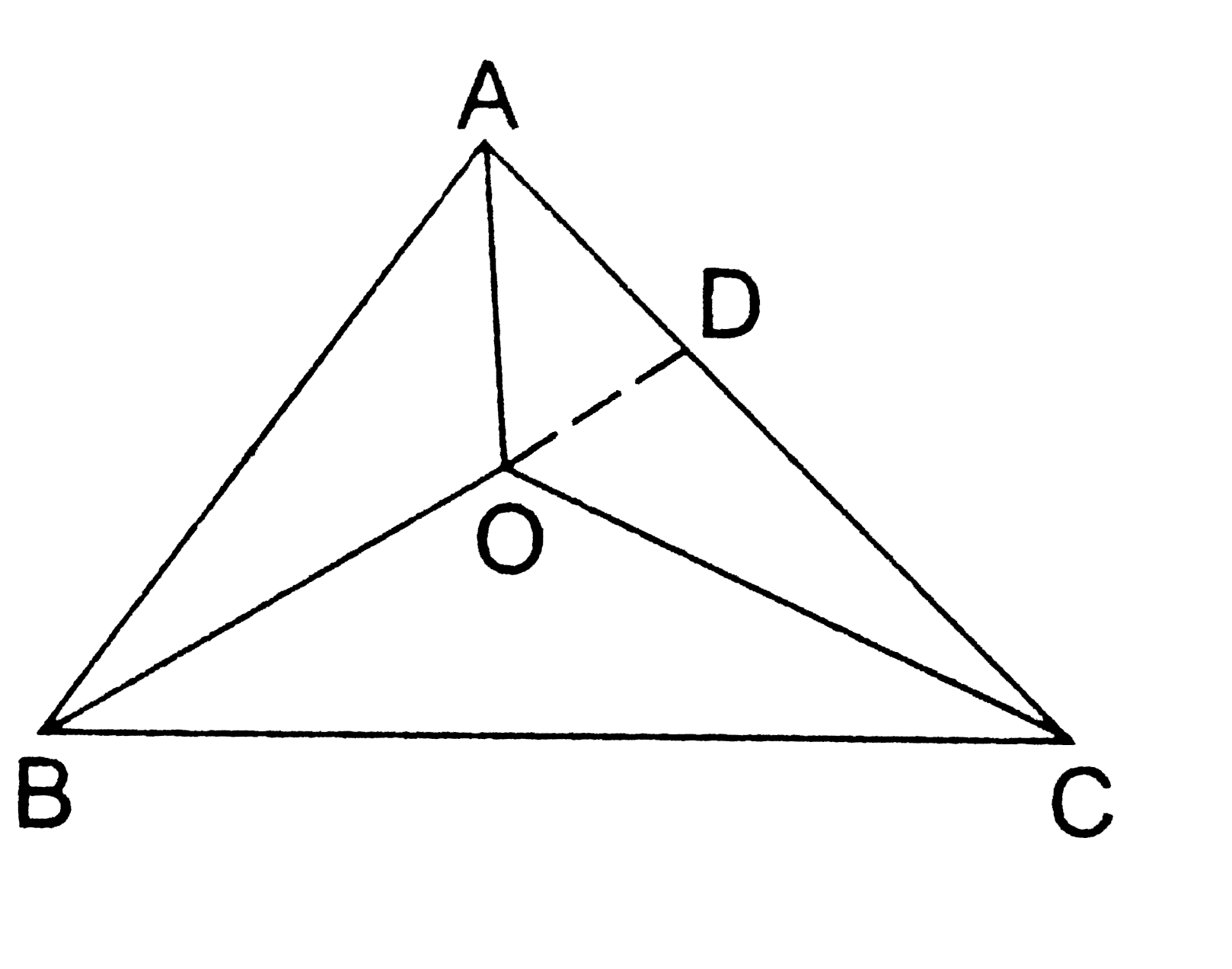
O is any point in the interior of ABC. Prove that AB+AC>OB+OC AB+BC+CA>OA+OB+OC OA+OB+OC>12(AB+BC+CA)
(i) In ΔABD, we have
∀B+AD>BD⇒AB+AD>OB+OD. …(i)
In ΔODC, we have OD+DC>OC. …(ii)
∴ AB+AD+OD+DC>OB+OD+OC
[adding (i) and (ii)]
⇒ AB+AD+DC>OB+OC
⇒ AB+AC>OB+OC [∵AD+DC>AC].
(ii) AB+AC>OB+OC.
Similarly, BC+BA>OC+OAandCA+CB>OA+OB.
Adding, we get (AB+BC+CA)>(OA+OB+OC).
(iii) In ΔOAB,ΔOBCandΔOCA, we have
OA+OB>AB,OB+OC>BCandOC+OA>CA.
∴ (OA+OB+OC)>12(AB+BC+CA).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
O is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
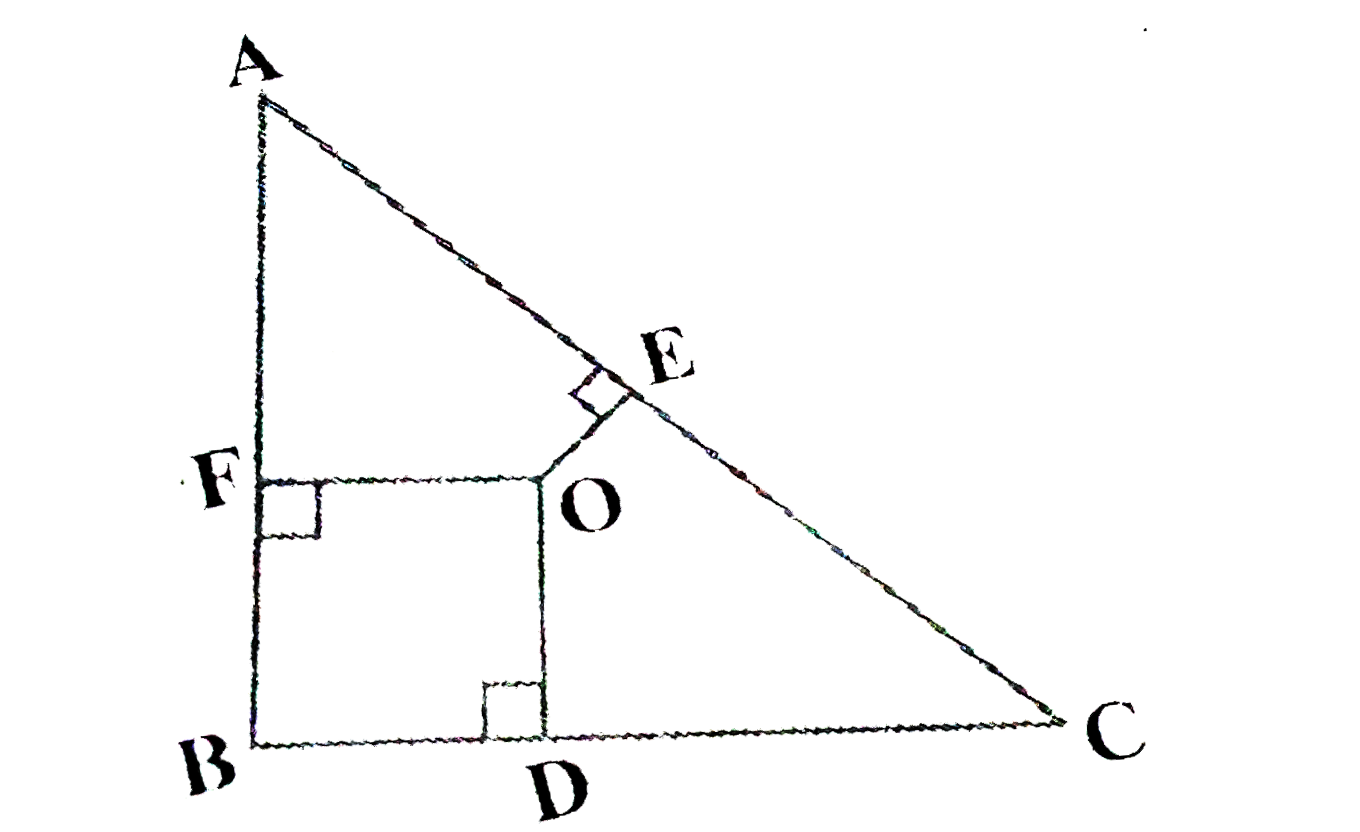
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionIn ABC, ∠A=60o . Prove that B C^2=A B^2+A C^2-A B.A C .
View SolutionABCD is a trapezium in which ABCD . The diagonals AC and BD intersect at O . Prove that (i) AOBCOD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
View SolutionABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2,
View SolutionIf O and O′ are circumcentre and orthocentre of ABC, then →OA+→OB+→OC equals
a.2→OO' b. →OO' c. →O'O d. 2→O'O
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle ABCDandO is a point inside it. OA,OB,OCandOD have been joined. To Prove: ar(AOD)+ar(BOC)=ar(AOB)+ar(COD)
View Solution
