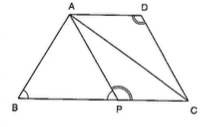
is a point on the side of a triangle such that Through lines are drawn parallel to respectively, so as to intersect at as shown in Figure. Show that is a cyclic quadrilateral.
In
(Angles opposing to equal sizes are equal)
(Linear pair)
........
(co interrior angles)
(Angles opposing to equal sizes are equal)
(Linear pair)
........
(co interrior angles)
(co interior )
.......(from ())
(Angles opposing to equal sizes are equal)
(Linear pair)
........
(co interrior angles)
(Angles opposing to equal sizes are equal)
(Linear pair)
........
(co interrior angles)
(co interior )
.......(from ())
( )
Since sum of opposite angles of the quadilateral is
Hence the quadilateral is a cyclic quadilateral.
Topper's Solved these Questions
Similar Questions
P is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
 View Solution
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming PQR.Figure .Show that BC=12QR
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
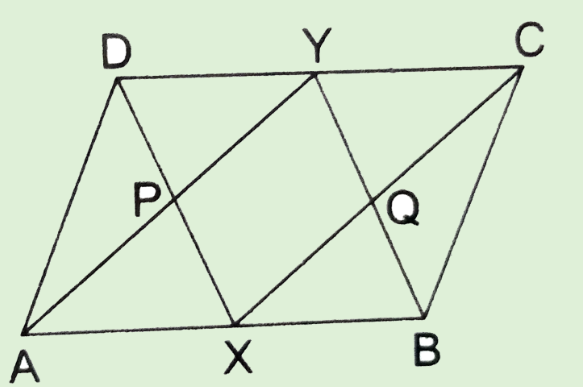
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
 View Solution
View Solution

