PQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
The correct Answer is:2cm
To find the radius of the inscribed circle in triangle PQR, we will follow these steps:
Step 1: Identify the sides of the triangle
Given:
- QR = 12 cm (one leg of the triangle)
- PQ = 5 cm (the other leg of the triangle)
Since triangle PQR is a right-angled triangle at Q, we can denote:
- PQ = a = 5 cm
- QR = b = 12 cm
Step 2: Use the Pythagorean theorem to find PR
According to the Pythagorean theorem:
PR2=PQ2+QR2
Substituting the values:
PR2=52+122
PR2=25+144
PR2=169
Taking the square root:
PR=√169=13 cm
Step 3: Calculate the semi-perimeter (s) of triangle PQR
The semi-perimeter s is given by:
s=a+b+c2
Where c=PR:
s=5+12+132
s=302=15 cm
Step 4: Use the formula for the radius (r) of the inscribed circle
The radius r of the inscribed circle in a triangle can be calculated using the formula:
r=As
Where A is the area of the triangle.
Step 5: Calculate the area (A) of triangle PQR
The area A of a right-angled triangle can be calculated as:
A=12×base×height
Using PQ as the base and QR as the height:
A=12×5×12
A=12×60=30 cm2
Step 6: Substitute the values into the radius formula
Now substituting the area and semi-perimeter into the radius formula:
r=As=3015=2 cm
Final Answer
The radius of the inscribed circle is 2 cm.
---
Given:
- QR = 12 cm (one leg of the triangle)
- PQ = 5 cm (the other leg of the triangle)
- PQ = a = 5 cm
- QR = b = 12 cm
According to the Pythagorean theorem:
PR2=PQ2+QR2
Substituting the values:
PR2=52+122
PR2=25+144
PR2=169
Taking the square root:
PR=√169=13 cm
The semi-perimeter s is given by:
s=a+b+c2
Where c=PR:
s=5+12+132
s=302=15 cm
The radius r of the inscribed circle in a triangle can be calculated using the formula:
r=As
Where A is the area of the triangle.
The area A of a right-angled triangle can be calculated as:
A=12×base×height
Using PQ as the base and QR as the height:
A=12×5×12
A=12×60=30 cm2
Now substituting the area and semi-perimeter into the radius formula:
r=As=3015=2 cm
The radius of the inscribed circle is 2 cm.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Short Answer Questions
4 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
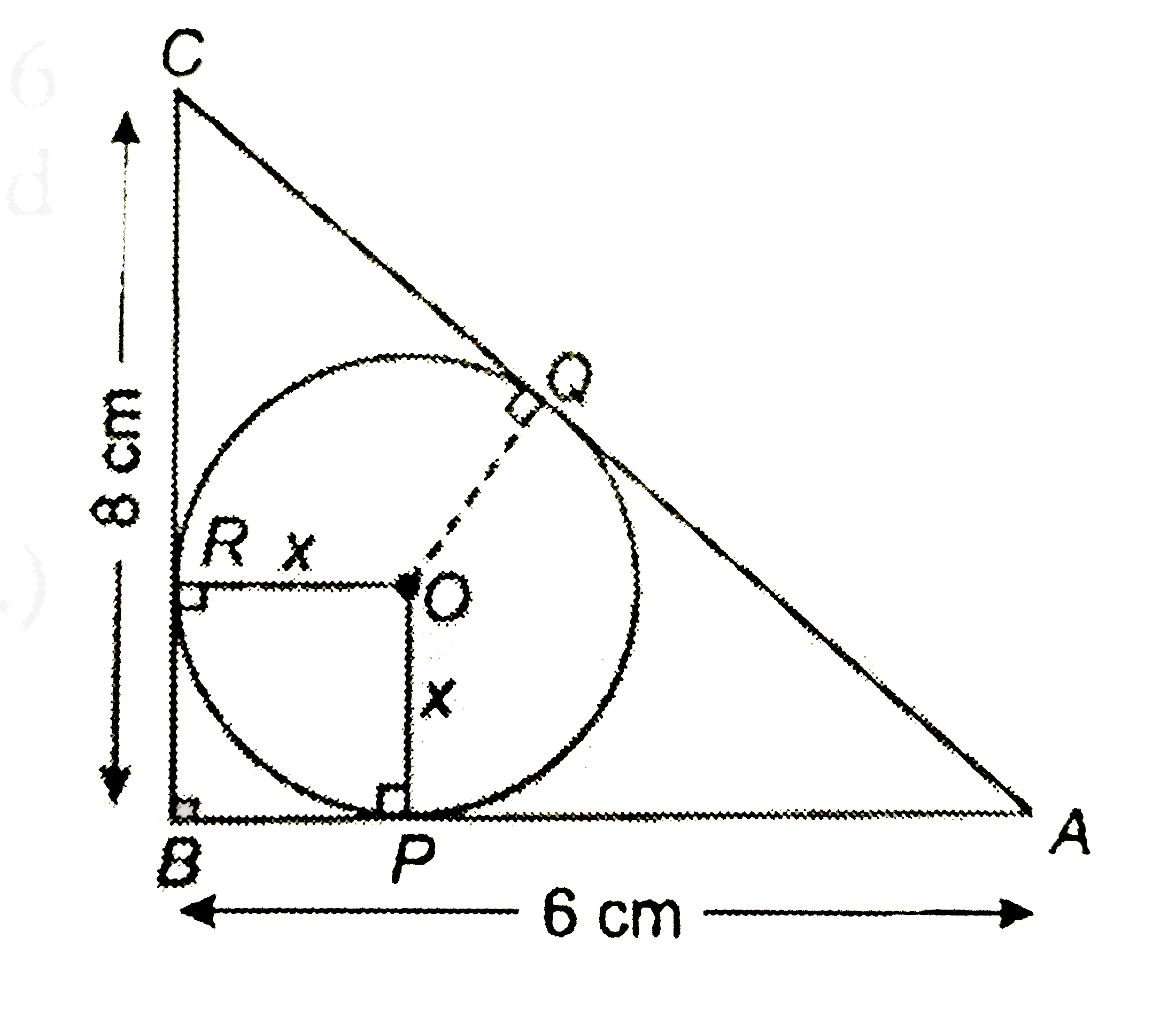
In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
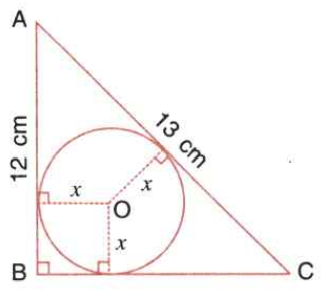
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionABC is a right angled triangle, right angled at B such that BC=6cm and AB=8cm . A circle with centre O is inscribed in ABC . The radius of the circle is (a) 1cm (b) 2cm (c) 3cm (d) 4cm
View SolutionPQR is a triangle right angled at P. If PQ=10cmandPR=24cm, find QR
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionGiven a right angled △ABC. The lengths of the sides containing the right angle are 6 cm and 8 cm. A circule is inscribed in △ABC. Find th radius of the circle.
View SolutionIn a right angled triangle ABC, right angled at B, BC=12cm and AB=5cm. The radius of the circle inscribed in the triangle (in cm) is :
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionConstruct a circle with centre O and radius 4 cm.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View Solution
