Sketch the curves and identify the region bounded by the curves x=12,x=2,y=logxany=2x. Find the area of this region.
The correct Answer is:(4−√2log2−52log2+32)sq. units
The given curves are
x=12
x=2
y=logex
y=2x
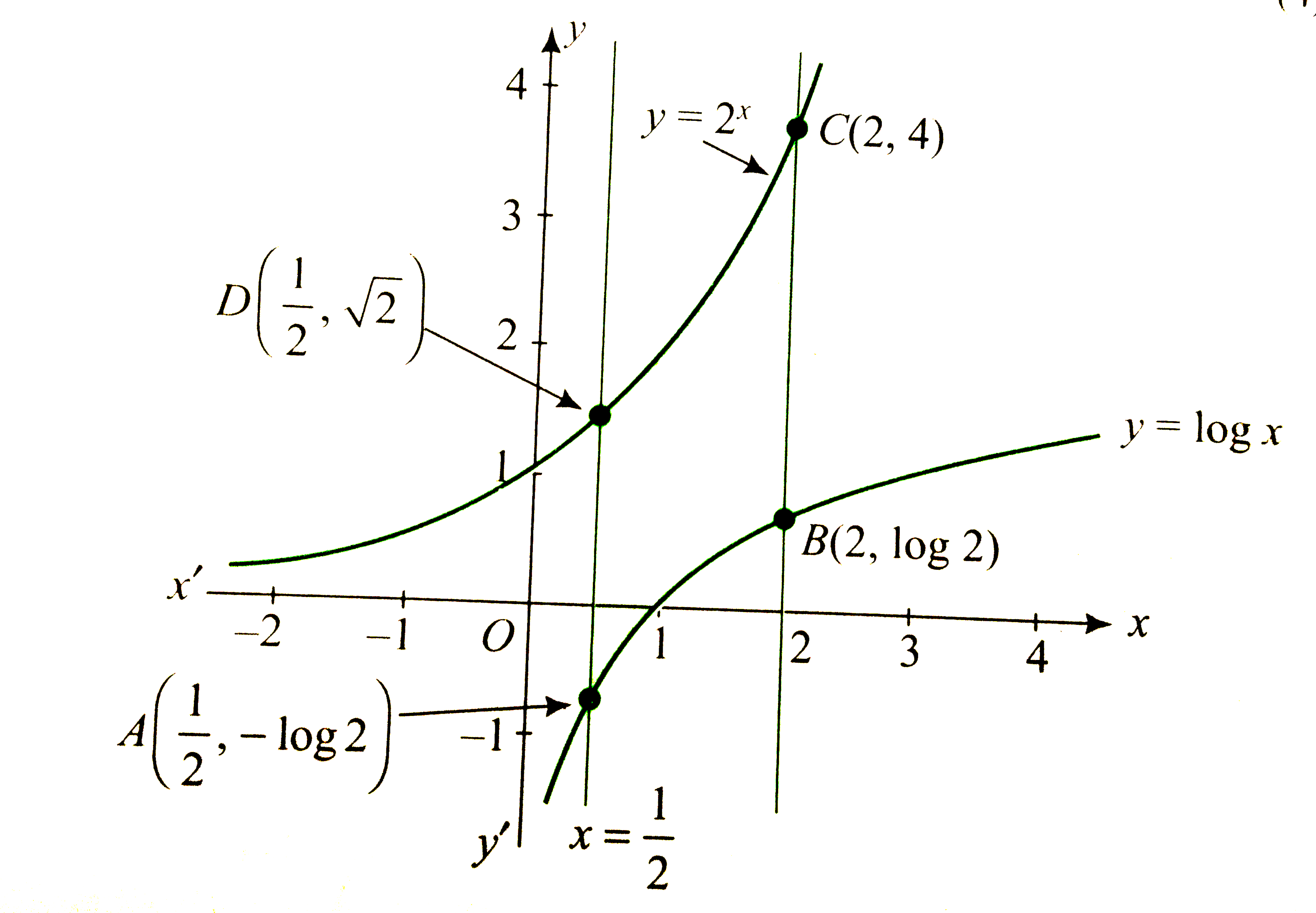
Required area = Area of ABCDA
=∫21/2(2x−logx)dx
[2xlog2−(xlogx−x)]21/2
=(4log2−2log2+2)−(−√2log2−12log12+12)
=(4−√2log2−52log2+35) sq. units.
Topper's Solved these Questions
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Concept Application Exercise 9.3
Explore 7 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Exercises - Single Correct Answer Type
Explore 40 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Concept Application Exercise 9.1
Explore 9 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
Similar Questions
Sketch the curves and identity the region bounded by x=12,x=2,y=lnx,andy=2x. Find the area of this region.
View SolutionSketch the region bounded by the curves y=x2+2, y=x, x=0 and x=1. also, find the area of this region.
View SolutionSketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
View SolutionFind the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionFind the area of the region bounded by the curves 2y2=x,3y2=x+1,y=0.
View SolutionThe area of the region bounded by the curves y=|x−2|,x=1,x=3 and the x-axis is
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0,andx=3.
View Solution