Sketch the region bounded by the curves y=√5−x2 and y=|x−1| and find its area.
The correct Answer is:5π−24 sq. units
The given curves are
y=√5−x2 (1)
y=|x−1| (2)
We can clearly see that on squaring the both sides of (1), equation (2) represents a circle.
But as y is + ve square root, (1) represents the upper-half of the circle with centre (0,0) and radius √5.
Equation (2) represents the curve
y={−x+ifx<1x−1ifx≥1
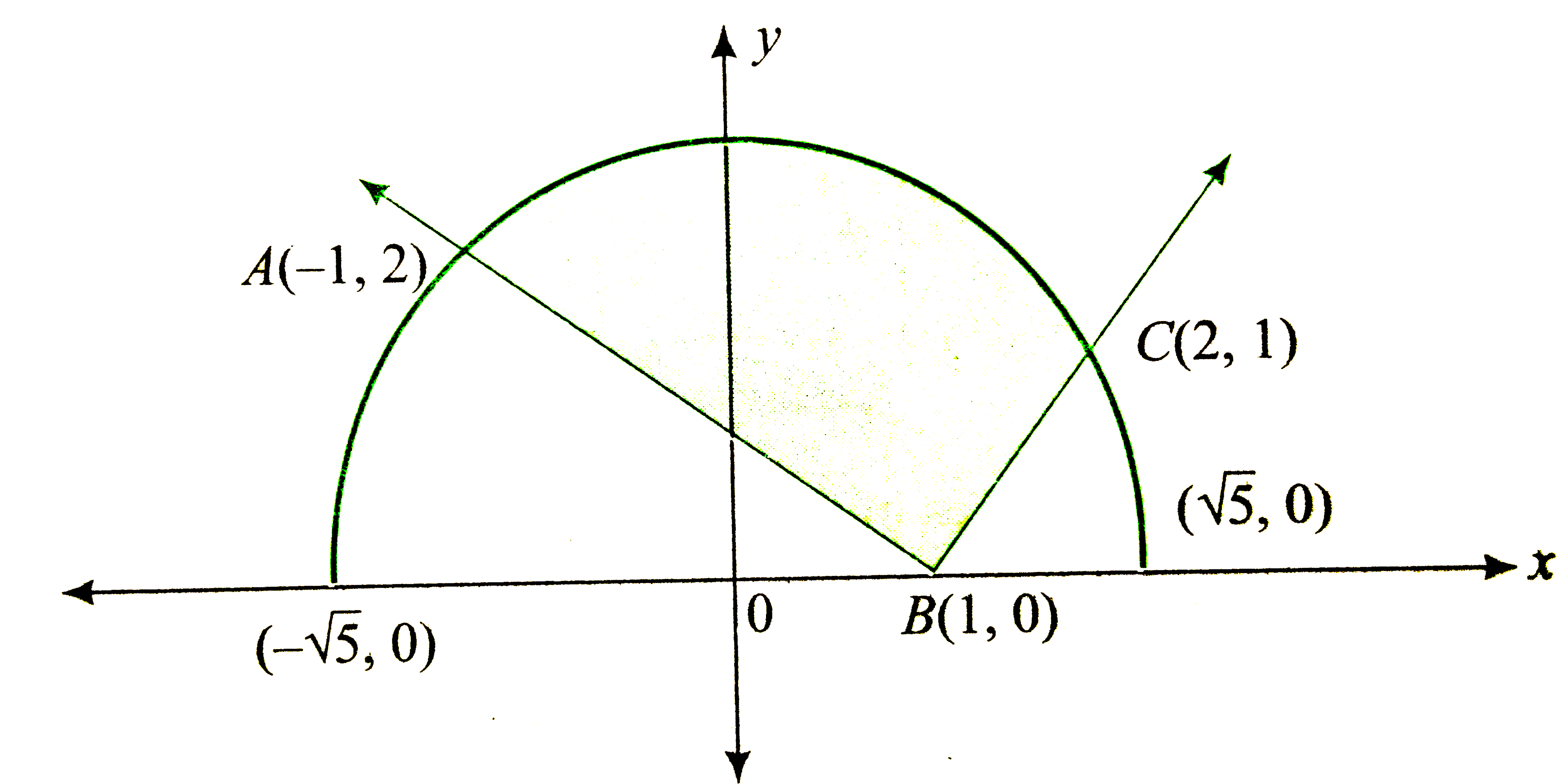
Graph of these curves are as shown in the figure with point of intersection of y=√5−x2andy=−x+1asA(−1,2)
and of y=√5−x2andy=x−1asC(2,1)
∴ Required area = Shaded area
=∫2−1√5−x2dx−∫2−1|x−1|dx
=[x2√5−x2+52sin−1(x√5)]2−1−∫1−1−(x−1)dx−∫21(x−1)dx
=(25√5−4+52sin−12√5)−(−12√5−1+52sin−1(−1√5))−(−x22+x)1−1−(x22−x)21
=1+52sin−12√5+1+52sin−1(1√5)
−[(−12+1)−(−12−1)]−[(2−2)−(12−1)]
=2+52[sin−12√5+sin−11√5]−2−12
=52[sin−12√5+cos−12√5]−12=52(π2)−12
5π−24 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type
40 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Find area bounded by curves y=√2−x2 and y = |x|.
View SolutionThe area of the region bounded by the curve y=√16−x2 and X-axis is
View SolutionSketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionSketch the region bounded by the curves y=x2+2, y=x, x=0 and x=1. also, find the area of this region.
View SolutionFind the area bounded by the curves x=∣∣y2−1∣∣ and y=x−5
View SolutionThe area (in sq. units) of the region bounded by the curves y=2x and y=|x+1|, in the first quadrant is :
View SolutionIf A is the area bounded by the curves y=√1−x2 and y=x3−x , then of πA.
View SolutionIf A is the area bounded by the curves y=√1−x2 and y=x3−x , then of πA.
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View Solution
