The area bounded by the curves is (b) (d)
sq. units
sq. units
sq. units
sq. units
The correct Answer is:B
Given curves are
Solving
Also, for
,
From these information, we can plot the graph of the functions.
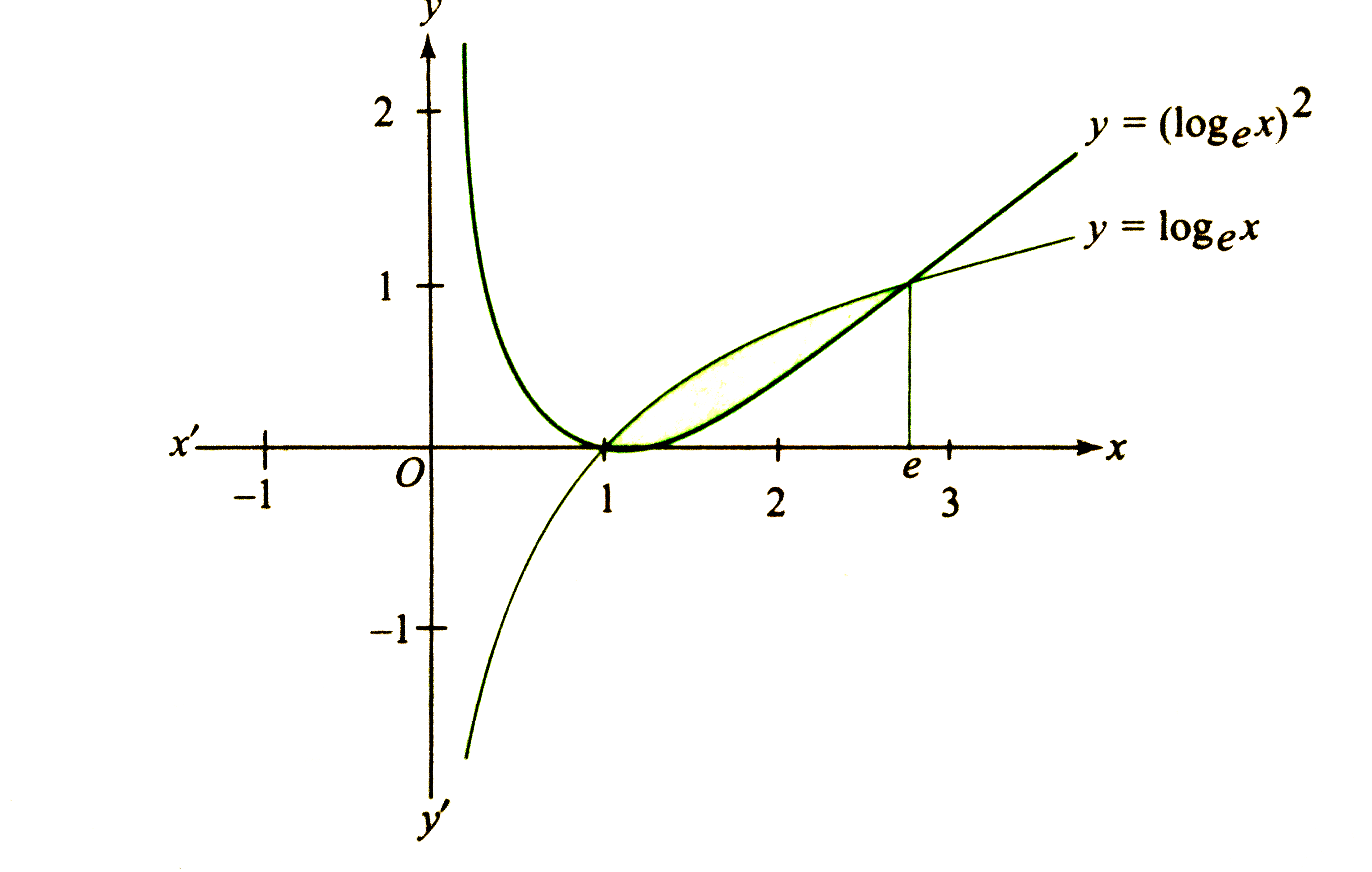
sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
The area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
View SolutionThe area bounded by the curve y2=8x and x2=8y is 163sq.units b. 316sq.units c. 143sq.units d. 314sq.units
View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is 14sq.units (b) 43sq.units 54sq.units (d) 73sq.units
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
View SolutionThe area of the region bounded by x=0,y=0,x=2,y=2,y≤exandy≥1nx is 6−41n2sq.units (b) 41n2−2sq.units 21n2−4sq.units (d) 6−21n2sq.units
View SolutionThe area of the region enclosed between the curves x=y2−1andx=|y|√1−y2 is 1sq.units (b) 43sq.units 23sq.units (d) 2sq.units
View SolutionThe area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionLet f(x)=minimum(x+1,√1−x) for all x≤1. Then the area bounded by y=f(x) and the x-axis is
View SolutionThe area bounded by the curve f(x)=x+sinx and its inverse function between the ordinates x=0andx=2π is 4πsq.units (b) 8πsq.units 4sq.units (d) 8sq.units
View SolutionIf f(x)=sinx,∀x∈[0,π2],f(x)+f(π−x)=2,∀x∈(π2,π)andf(x)=f(2π−x),∀x∈(π,2π), then the area enclosed by y=f(x) and the x-axis is πsq.units (b) 2πsq.units 2sq.units (d) 4sq.units
View Solution
