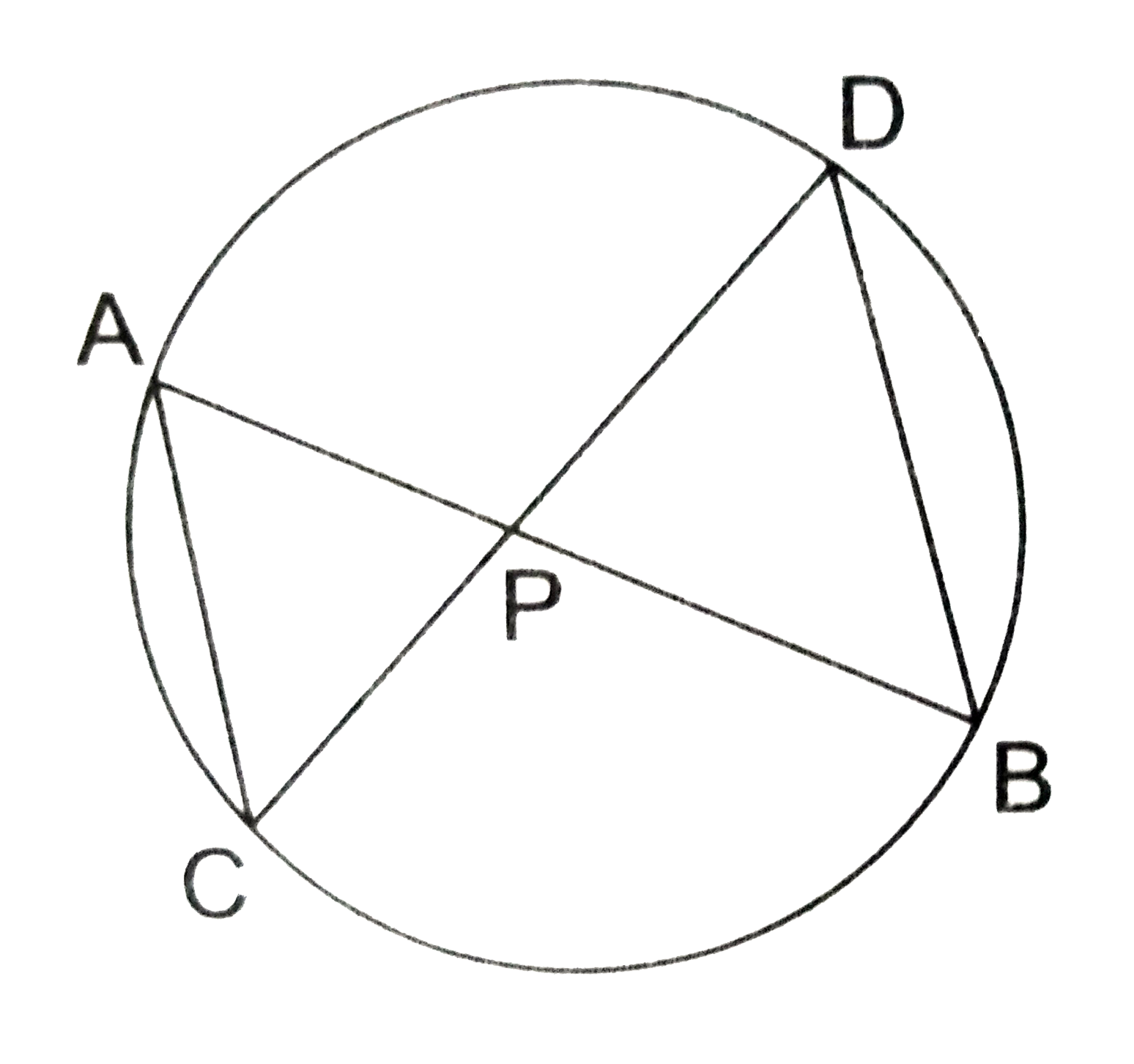
Two chords AB and CD of a circle intersect at a point outside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
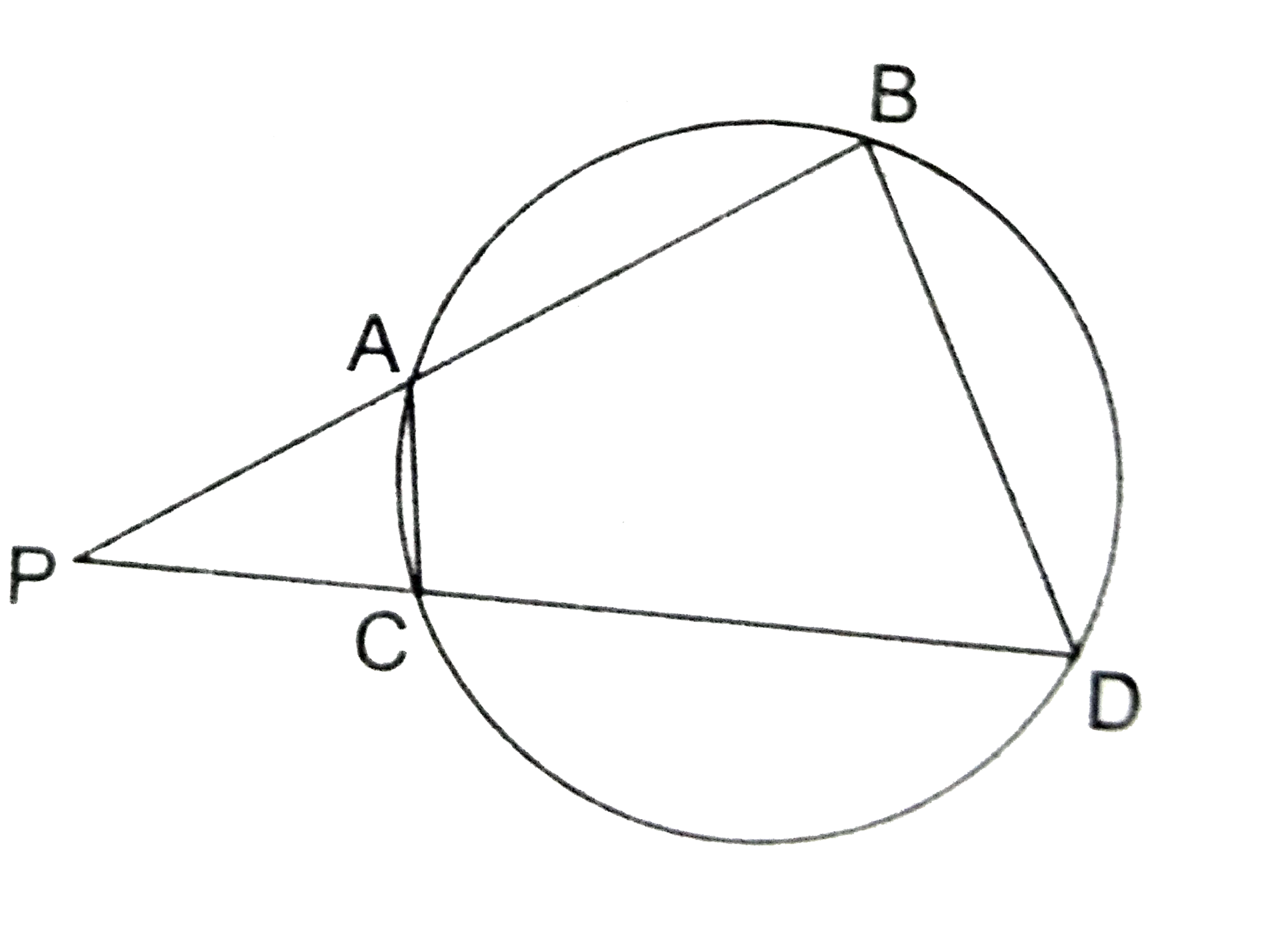
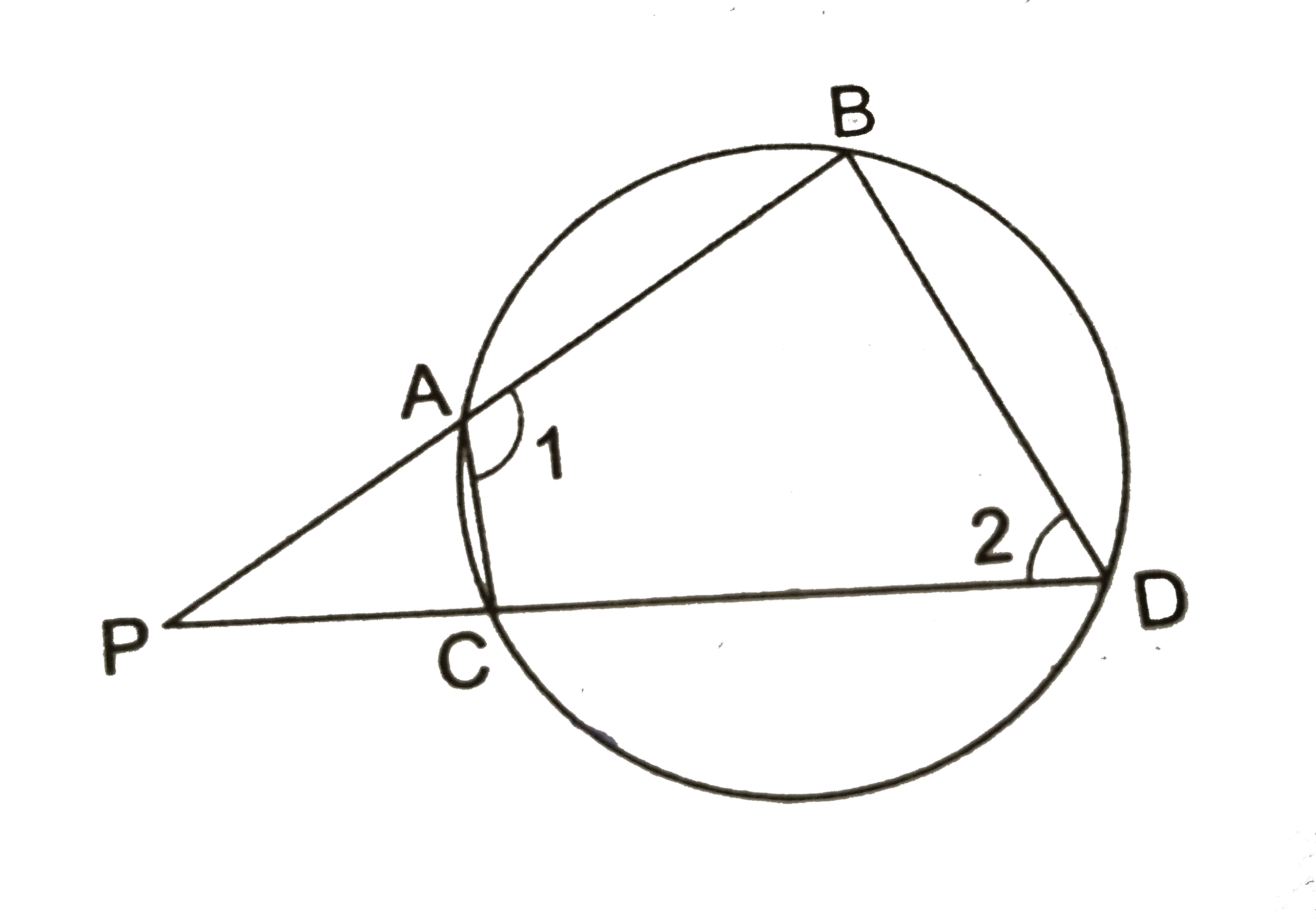
Clearly ABCD is a cyclic quadrilateral.
∴∠1+∠2=180∘ ...(i)
In ΔPACandΔDPB, we have
∠PAC=∠DPB[ common]
∠PAC=∠PDB [ each equal to (180∘−∠)]
[ Note ∠PAC+∠1=180∘ (linear pair)
and ∠PDB+∠1=180∘ [ using]
∴ΔPAC~ΔPDB [ by AA-similarity]
And so, PAPD=PCPBrArPA⋅PC⋅PD.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D22videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of these - Question 2 - Select One
Two chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cm - Question 3 - Select One
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cm
Chords AB and CD of a circle , when produced, meet at point P outside the circle. If AB = 6 cm, CD = 3 cm and PD = 5 cm, then PB is equal to :
एक वृत्त की जीवाएं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB का मान क्या होगा ?View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionTwo chords AB and CD of a circle intersect at A, AB is the diameter and CD is ⊥ to AB .AE = 2 cm AB = 10 cm,Find value of ED.
View SolutionThe two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
View Solution