Question

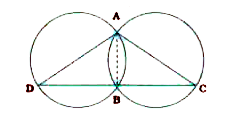
Two circles are drawn with sides $AB,AC$
of a triangle $ABC$
as diameters. The circles intersect at a point $D\stackrel{.}{}$
Prove that $D$
lies on $BC\stackrel{.}{}$

Explanation

Gives: Circles are described with sides `AB` and `AC` of a `triangleABC` as diameters. They intersect at a point `D`.
To Prove: `D` lies on the third side `BC` of `triangleABC`
Construction: Join `AD`.
Proof: Circle described on `AB` as-diameter intersects `BC` in `D`.
`angleADB=90^@` [Angle in a semi-circle]
But `angleADB+ angleADC=180^@` [Linear Pair]
`angleADC=90^@`
Hence, the circle described on `AC` as diameter must pass through `D`.
Thus, the two circles intersect in `D`.
Now, `angleADB+angleADC=180^@`
`therefore` Points `B`, `D`, `C` are collinear.
`thereforeD` lies on `BC`.
Hence Proved.