Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
15∘
30∘
45∘
60∘
The correct Answer is:D
To solve the problem, we need to find the angle ∠OAB where O is the center of the circle defined by the equation x2+y2=a2, and A and B are points on the circle such that the chord AB has a length equal to a. The chord BC is also equal to a.
1. Understand the Circle:
The equation of the circle is given by x2+y2=a2. This means the center O of the circle is at the origin (0,0) and the radius r is a.
Hint: Remember that the radius of the circle is the distance from the center to any point on the circle.
2. Draw the Chords:
Let's denote the points A and B on the circle such that the length of chord AB=a. Similarly, denote point C such that BC=a.
Hint: Visualizing the chords and the circle will help in understanding the relationships between the points.
3. Midpoints:
Let M be the midpoint of chord AB and N be the midpoint of chord BC. The coordinates of M and N can be calculated if we know the coordinates of points A, B, and C.
Hint: The midpoint of a segment can be found using the formula M=(x1+x22,y1+y22).
4. Triangles Involved:
The triangle OAB is formed by the center O and the endpoints of the chord AB. Since OA=OB=a (the radius) and AB=a, triangle OAB is an equilateral triangle.
Hint: In an equilateral triangle, all sides are equal, and all angles are 60∘.
5. Finding the Angle:
Since triangle OAB is equilateral, we can conclude that:
∠OAB=60∘
Hint: Recall that in an equilateral triangle, each angle measures 60∘.
Final Answer:
Thus, the angle ∠OAB is 60∘.
The equation of the circle is given by x2+y2=a2. This means the center O of the circle is at the origin (0,0) and the radius r is a.
Let's denote the points A and B on the circle such that the length of chord AB=a. Similarly, denote point C such that BC=a.
Let M be the midpoint of chord AB and N be the midpoint of chord BC. The coordinates of M and N can be calculated if we know the coordinates of points A, B, and C.
The triangle OAB is formed by the center O and the endpoints of the chord AB. Since OA=OB=a (the radius) and AB=a, triangle OAB is an equilateral triangle.
Since triangle OAB is equilateral, we can conclude that:
∠OAB=60∘
Thus, the angle ∠OAB is 60∘.
Topper's Solved these Questions
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (Single Integer Answer Type Questions)
Explore 9 Videos
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (Statement I And Ii Type Questions)
Explore 7 Videos
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- BIONOMIAL THEOREMBook:ARIHANT MATHS ENGLISHChapter:BIONOMIAL THEOREMExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- COMPLEX NUMBERSBook:ARIHANT MATHS ENGLISHChapter:COMPLEX NUMBERSExercise:Complex Number Exercise 8
Explore 2 Videos
Similar Questions
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View Solution
Knowledge Check
AB and CD are chords of the circle, and E and F are the midpoints of the chords, respectively. The line EF passes through the center O of the circle. IF EF=17. then what is radius of the circle?
 A10B12C13D15
A10B12C13D15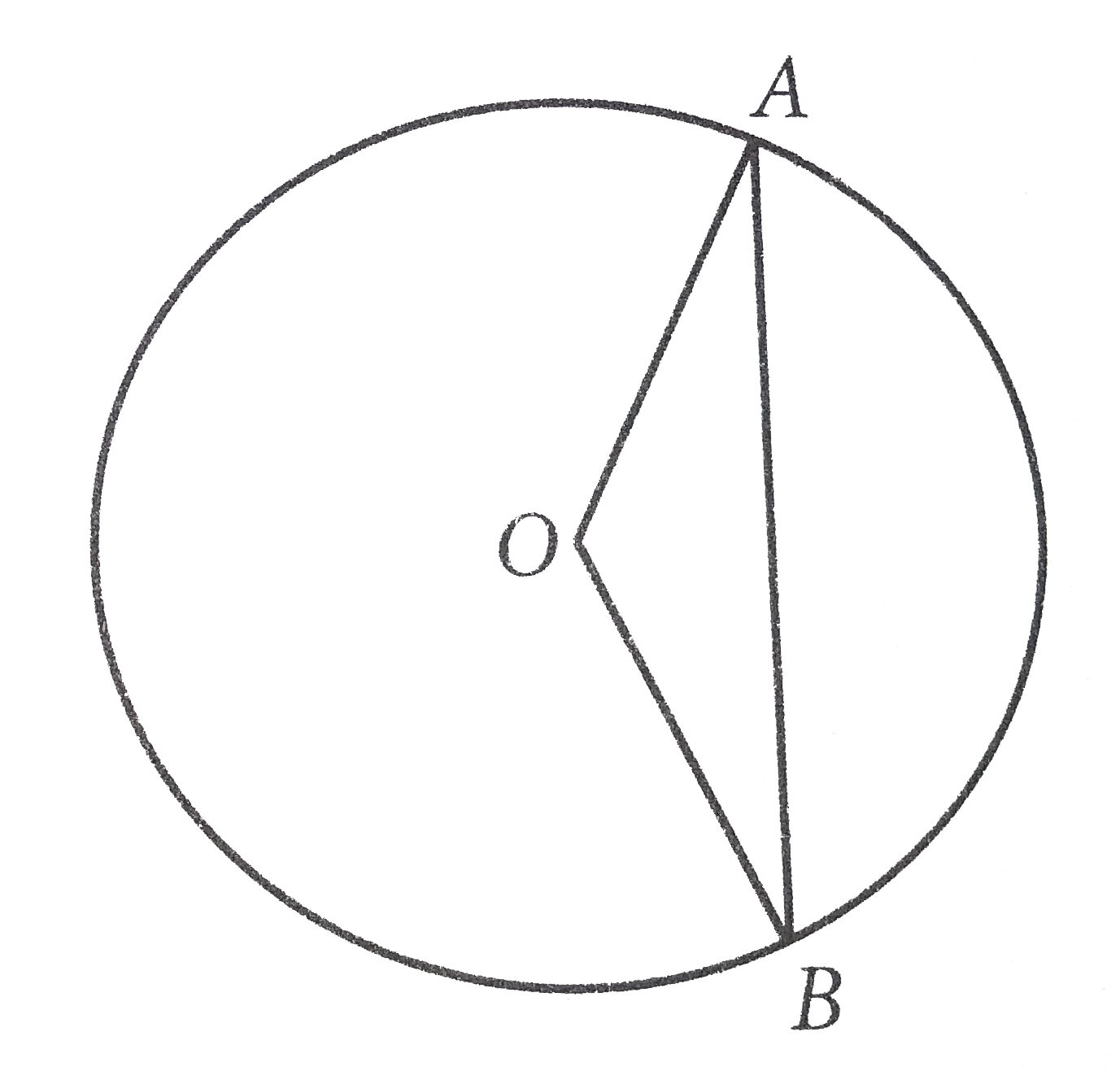
If the radius of the circle above is x, ∠AOB=120∘, and O is the center of the circle, what is the length of chord AB, in terms of x?A√2xB√3xCx√2Dx√3
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
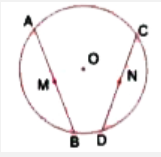
∠AMN=∠CNM.
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
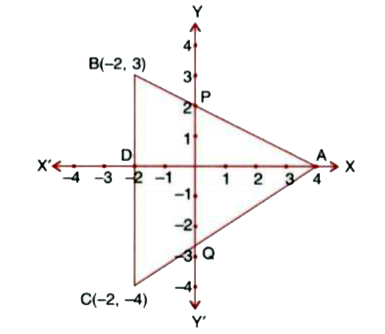
Write the co-ordinates of A.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
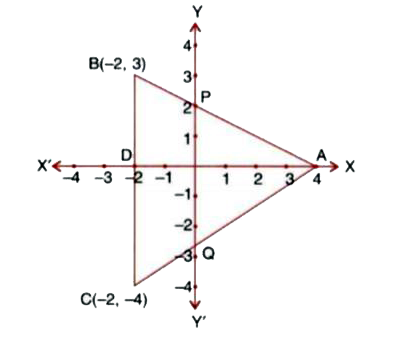
Find the length of AB and AC.
View Solution