Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
(a)60∘
(b)90∘
(c)120∘
(d)150∘
The correct Answer is:A
To solve the problem step by step, we will analyze the given information and derive the required locus of the points of intersection of the tangents at points A and C.
Step 1: Understand the Circle and Chords
The equation of the circle is given by x2+y2=a2. The points A, B, and C are on the circle such that the lengths of chords AB and BC are equal to a.
Hint: Visualize the circle and mark points A, B, and C such that the lengths of the chords are equal.
Step 2: Determine the Midpoints
Let M and N be the midpoints of chords AB and BC, respectively. The coordinates of M and N can be expressed in terms of the coordinates of points A and B, and B and C.
Hint: Use the midpoint formula: if M is the midpoint of AB, then M=(xA+xB2,yA+yB2).
Step 3: Analyze the Line Joining M and N
The line segment joining M and N will intersect the circle at points P and Q. Since P is closer to AB, we need to find the coordinates of P and Q based on the geometry of the circle.
Hint: Use the properties of the circle and the midpoints to derive the equations of the line MN.
Step 4: Tangents at Points A and C
The tangents at points A and C can be derived using the point of tangency and the radius. The angle between these tangents can be determined using the geometry of the circle.
Hint: Recall that the angle between two tangents drawn from an external point to a circle can be calculated using the angle subtended by the points at the center.
Step 5: Calculate the Angle Between Tangents
Since triangle AOB is equilateral (as AB=BC=a), we know that each angle in triangle AOB is 60∘. The angle AOC can be found as follows:
- The angle AOB is 60∘.
- The angle BOC is also 60∘.
- Therefore, the angle AOC=120∘.
Hint: Use the property of angles in a triangle and the fact that the sum of angles on a straight line is 180∘.
Step 6: Conclusion
The angle between the tangents at points A and C is 60∘. Thus, the locus of the points of intersection of the tangents at A and C is determined.
Final Answer: The angle between the tangents at points A and C is 60∘.
The equation of the circle is given by x2+y2=a2. The points A, B, and C are on the circle such that the lengths of chords AB and BC are equal to a.
Let M and N be the midpoints of chords AB and BC, respectively. The coordinates of M and N can be expressed in terms of the coordinates of points A and B, and B and C.
The line segment joining M and N will intersect the circle at points P and Q. Since P is closer to AB, we need to find the coordinates of P and Q based on the geometry of the circle.
The tangents at points A and C can be derived using the point of tangency and the radius. The angle between these tangents can be determined using the geometry of the circle.
Since triangle AOB is equilateral (as AB=BC=a), we know that each angle in triangle AOB is 60∘. The angle AOC can be found as follows:
- The angle AOB is 60∘.
- The angle BOC is also 60∘.
- Therefore, the angle AOC=120∘.
The angle between the tangents at points A and C is 60∘. Thus, the locus of the points of intersection of the tangents at A and C is determined.
Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Single Integer Answer Type Questions)
9 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos
Similar Questions
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View Solution
Knowledge Check
AB and CD are chords of the circle, and E and F are the midpoints of the chords, respectively. The line EF passes through the center O of the circle. IF EF=17. then what is radius of the circle?
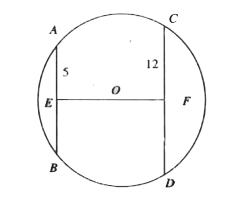 A10B12C13D15
A10B12C13D15
Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionA chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
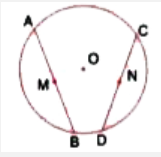
∠AMN=∠CNM.
View Solution
