Complete Solutions to EXAMPLE of chapter CIRCLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | CIRCLES |
| AGRAWAL PUBLICATION | EXAMPLE |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
05:14View SolutionAB is the diameter of a circle and AC is its chord such that `angle BAC` = `30^@`. If the tangent at C intersects AB extended at D, then BC = BD.
05:08View SolutionA circle is inscribed in an isosceles triangle ABC with AB = AC, touching the sides BC, AC and AB at P, Q and R respectively. Prove that the point of contact P bisects the side BC.
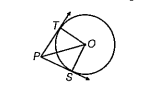
04:04View SolutionIn the figure, form a point P, two tangents PT and PS are drawn to a circle with centre O such that `angle SPT = 120^@`. Prove that OP = 2PS.
 02:41View Solution
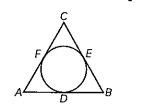
02:41View SolutionIn the figure, a circle is inscribed in a `triangle ABC`, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lenghts of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively. Find the length of AD, BE and CF.
 06:33View Solution
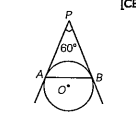
06:33View SolutionIn the figure, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and `angle APB = 60^@`. Find the length of chord AB.
 03:45View Solution
03:45View SolutionProve that the rectangle circumscribing a circel is a square.
03:39View SolutionIn given figure, a quadrilateral ABCD is drawn to circumscribe a cirle, with centre O, in such a way that the sides AB, BC, CD and DA tocuh the circle at the points P, Q, R and C respectively. Prove that AB + CD = BC + DA.
 03:11View Solution
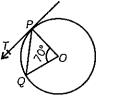
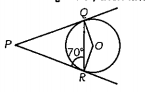
03:11View SolutionIn the figure, O is the centre of the circle. PQ is a chord and PT is the tangent if `angle POQ`= `70^@`, find `angle TPQ`.
 03:40View Solution
03:40View SolutionPQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If POR = `120^@`, what is the measure of OPQ?
03:46View SolutionIn given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If PRQ = `120^@`, then prove that OR = PR + RQ.
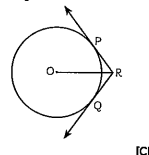 04:14View Solution
04:14View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with chord.
04:32View SolutionIn the figure given, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
 03:09View Solution
03:09View SolutionIn the given figure, a circle touches the side BC of `tiangle ABC` at F and touches AB and AC at D and E respectively. If AD = 8 cm, then find the perimeter of `triangle ABC`.
 03:11View Solution
03:11View SolutionFrom an external point P, tangents PA and PB are drawn to a circle with centre O. if `angle PAB` = `50^@`, then find the `angle AOB`.
03:44View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is `60^@`, then find the length of OP.
03:54View SolutionIn the figure, `angle ADC = 90^@`
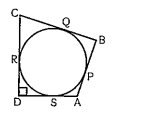
BC = 38 cm, CD = 28 cm and BP = 25 m. Find the radius of the circle.05:06View SolutionIf a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R respectively, prove that AQ = `1/2 (BC + CA + AB)`.
04:42View SolutionOut of two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
02:52View SolutionIn given figure two circle touch each othe at point C. prove that common tangent to circles at C, bisects the common tangents at P and Q.
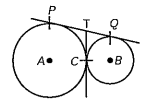 03:41View Solution
03:41View Solutionprove that the parallelogram circumscribing a circle is a rhombus.
05:14View SolutionIn the given figure common tangents AB and CD to two circles intersect at E. prove that AB = CD.
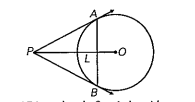 05:55View Solution
05:55View SolutionIn the figure, AB is a chord of a circle, with centre O such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. find the length of PA.
 05:22View Solution
05:22View SolutionIn the given figure , the radii of the two circles are equal, prove that AB = CD.
05:01View SolutionABC is a right triangle in which `angle B = 90^@`. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
02:34View SolutionIn the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting PQ at A and RS at B. prove that `angle AOB = 90^@`.
 05:20View Solution
05:20View SolutionIn figure, PQ and PR are tangents drawn to a circle with centre O from an external point P. If `angle PRQ = 70^@`, then find `angle QPR` and `angle OQR`.
 03:53View Solution
03:53View SolutionIn the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and `angle BAC = 135^@`. Find the length of chord AB.
01:53View SolutionA chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisector the arc PRQ.
02:01View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
07:35View SolutionIn the figure, AB is the diameter of a circle with centre O and AT is a tangent. If `angle AOQ` = `58^@`, find `angle ATQ`.
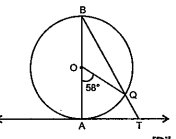 06:13View Solution
06:13View SolutionIn the figure AOB is the diameter of a circle with centre O. The tangent at a point T on the circle, meets AB produced at P. if `angle BAT` = `30^@`, find `angle TPA`.
 02:01View Solution
02:01View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
03:28View SolutionIn the given figure, PQ is a tangent from an external point P and QOR is a diameter. If `angle POR = 130^@` and S is a point on the circle, find `angle 1 + angle 2`.
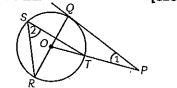 03:01View Solution
03:01View SolutionIn the figure are two concentric circles of radii 6 cm and 4 cm, with centre O. if AP is a tangent to the larger circle and BP to the smaller circle and the length of AP is 8 cm, find the length of BP.
02:53View SolutionIn the given figure, two tangents TP and TQ are drawn to a circle with centre O, from an external point T. prove that `angle PTQ` = `2 angle OPQ`.
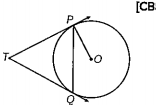 05:57View Solution
05:57View SolutionProve that tangent drawn at any point of a circle is perpendicular to the radius through the point of contact.
03:09View SolutionProve that the tangent drawn at the mid point of an arc of a circle is parallel to the chord joining the end points of the arc.
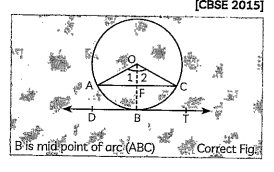 03:34View Solution
03:34View SolutionIn the figure two circles touch each other at A. A common tangents touches them at B and C and another common tangent at A meets the previous common tangents at P. Prove that `angle BAC = 90^@`.
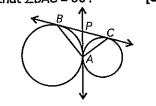 04:34View Solution
04:34View SolutionIn the figure PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents drawn at P and Q intersect at T. find the length of TP.
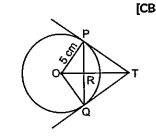 01:30View Solution
01:30View SolutionLet S denote the semiperimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively. Prove that BD = s-b.
03:45View SolutionFrom an external point P, two tangents PA and PB, are drawna to a circle with centre O. At one point E on the circle, a tangent is drawn which intersects PA and PB at C and D respectively. If PA = 10 cm find the perimeter of the triangle PCD.
05:57View SolutionIn the figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects the cirlce at E. If AB is a tanent to the cirle at E, find the length of AB, where TP and TQ are two tangents to the circle.
 03:45View Solution
03:45View SolutionIn the given figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C, is intersecting XY at A and X'Y' at B. prove that `angle AOB` = `90^@`
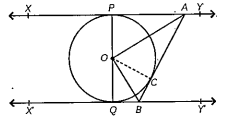 01:22View Solution
01:22View SolutionIf an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
02:03View SolutionIn a right triangle ABC in which `angle B = 90^@`, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. prove that the tangent to the circle at P bisects BC.
04:15View SolutionIn the given figure common tangents AB and CD to two circles with centre O and O', intersect at E. prove that the points O, E, O' are collinear.
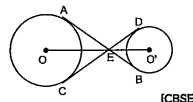 05:55View Solution
05:55View SolutionA is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. if a tangent BC is drawn at a point R lying on the minor arc PQ intersect AP at B and AQ at C, find the perimeter of the `triangle ABC`.
03:04View SolutionIn fig 7, two equals circles, with centres O and O', touch each other at X. OO' produced meets the circle with centre O' at A. Ac is tangent to the circle with centre O, at the point C. O'D is perpendicular to AC. Find the value of `(DO')/(CO).
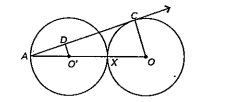 03:43View Solution
03:43View SolutionIn the figure the radius of the circle of `triangle ABC` of area `84 cm^2` is 4 cm and the lenghts of the segment AP and BP into which side AB is divided by the point of contact P are 6 cm and 8 cm. find the lengths of the sides AC and BC.
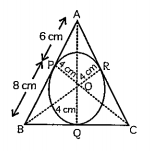 02:07View Solution
02:07View SolutionIn the figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. the tangents at P and Q intersect at point T. Find the length of TP.
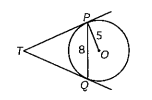 01:30View Solution
01:30View Solution
EXAMPLE questions and complete solutions for chapter CIRCLES of AGRAWAL PUBLICATION of Class 10
