Complete Solutions to Chapter Test of chapter GENERAL KINEMATICS AND MOTION IN ONE DIMENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GENERAL KINEMATICS AND MOTION IN ONE DIMENSION |
| A2Z | Chapter Test |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
A particle moves in a straight line, its position (in m) as function of time is given by `x = (at^2 + b)`.
What is average velocity in time interval `t = 3 sec` to `t = 5 sec` ? (Where `a` and `b` are constant and `a = 1 m//s^2, b = 1 m`.)
View SolutionThe position vector of a particle is given as `vecr=(t^2-4t+6)hati+(t^2)hatj`. The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to
View SolutionA body is thrown vertically upwards. If air resistance is to be taken into account, then the time during which the body rises is.
View SolutionThe position of a particle moving rectilinearly is given by `x = t^3 - 3 t^2 - 10`. Find the distance travelled by the particle in the first `4` seconds starting from `t = 0`.
View SolutionA body is moving from rest under constant acceleration and let `S_1` be the displacement in the first `(p - 1)` sec and `S_2` be the displacement in the first `p` sec. The displacement in `(p^2 - p + 1)` sec. will be
View SolutionA particle moves in a straight line with an acceleration `a ms^-2` at time 't' seconds where `a = - (1)/(t^2)` When `t = 1` the particle has a velocity of `3 ms^-1`. Find the velocity of the particle at `t = 4 s`.
View SolutionVelocity-time graph for a moving object is shown in the figure. Total displacement of the object during the time interval when there is non-zero acceleration and retardation is.
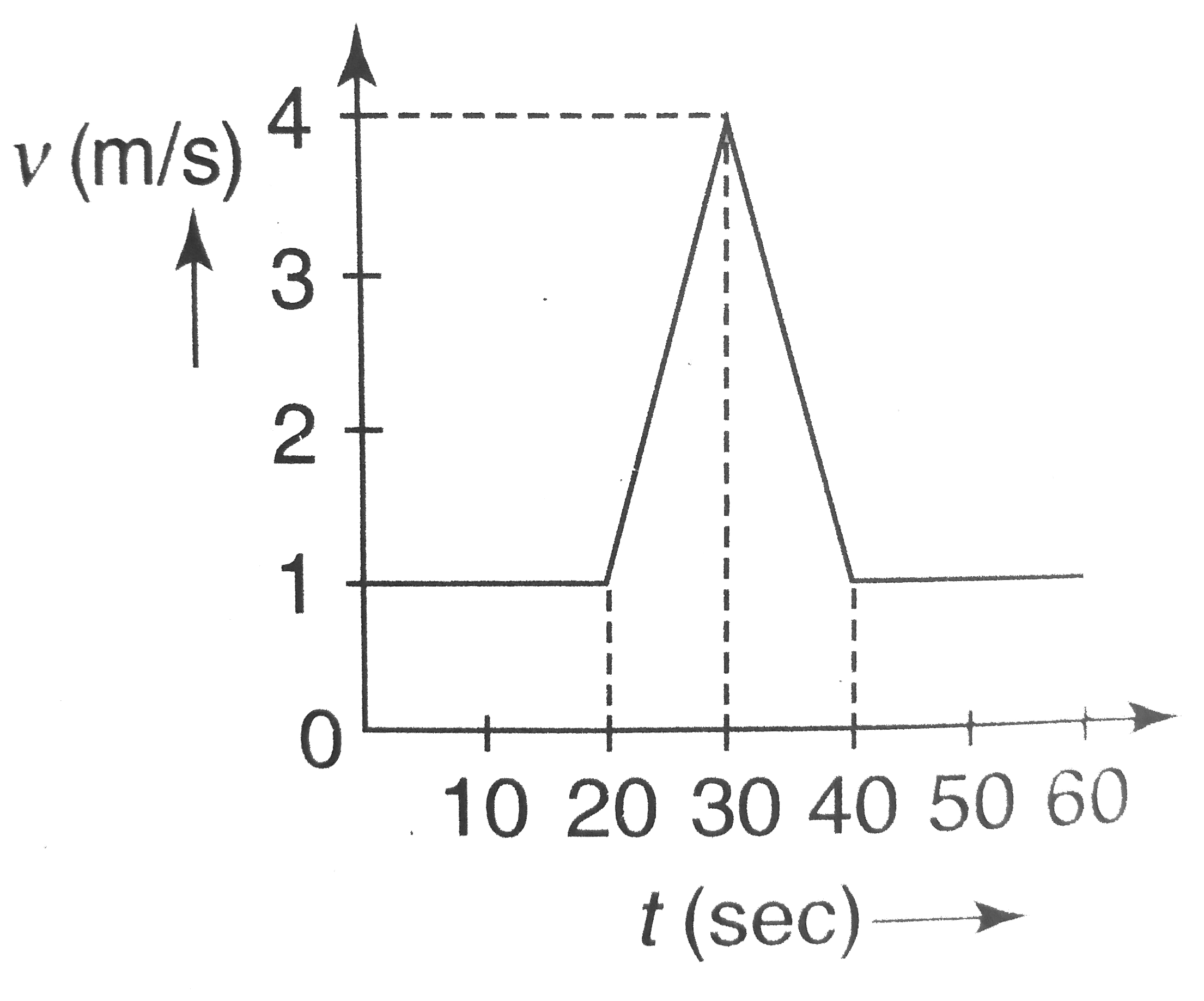
View SolutionTwo particles at a distance `5 m` apart, are thrown towards each other on an inclined smooth plane with equal speed 'v'. Inclined plane is inclined at an angle of `30^@` with the horizontal. It is known that both particle move along the same straight line. The particle colllide at the point from where the lower is thrown. Find the value of `["take " g = 10 m//s^2]`.
View SolutionA particle at `t = 0` second is at point `A` and moves along the shown path (ABCDF) with uniform speed `v = (1 + (pi)/(3)) m//s`. Both the straight segments `AB` and `DE` are along the diameter `BD` of semicircle `BCD` radius `R = 1` meter. Find the instant of time at which the instantaneous velocity of the particle is along the direction of average velocity from `t = 0` second to that instant.
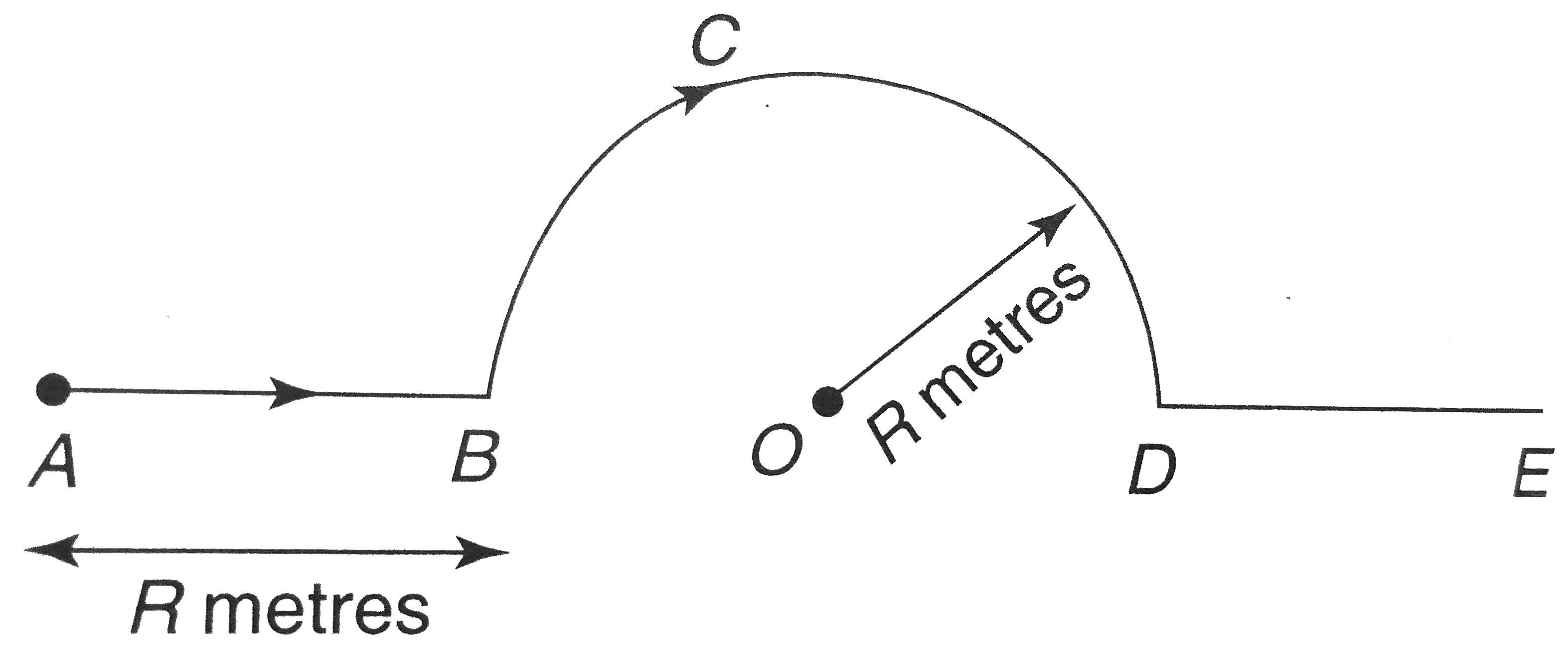
View SolutionA balloon is moving along with constant upward acceleration of `1 m//s^2`. A stone is thrown from the balloon downwards with speed `10 m//s` with respect to the balloon. At the time of projectile balloon is at height `120 m` from the ground and is moving with speed `20 m//s`. Find the time required to fall on the ground by the stone after the projection.
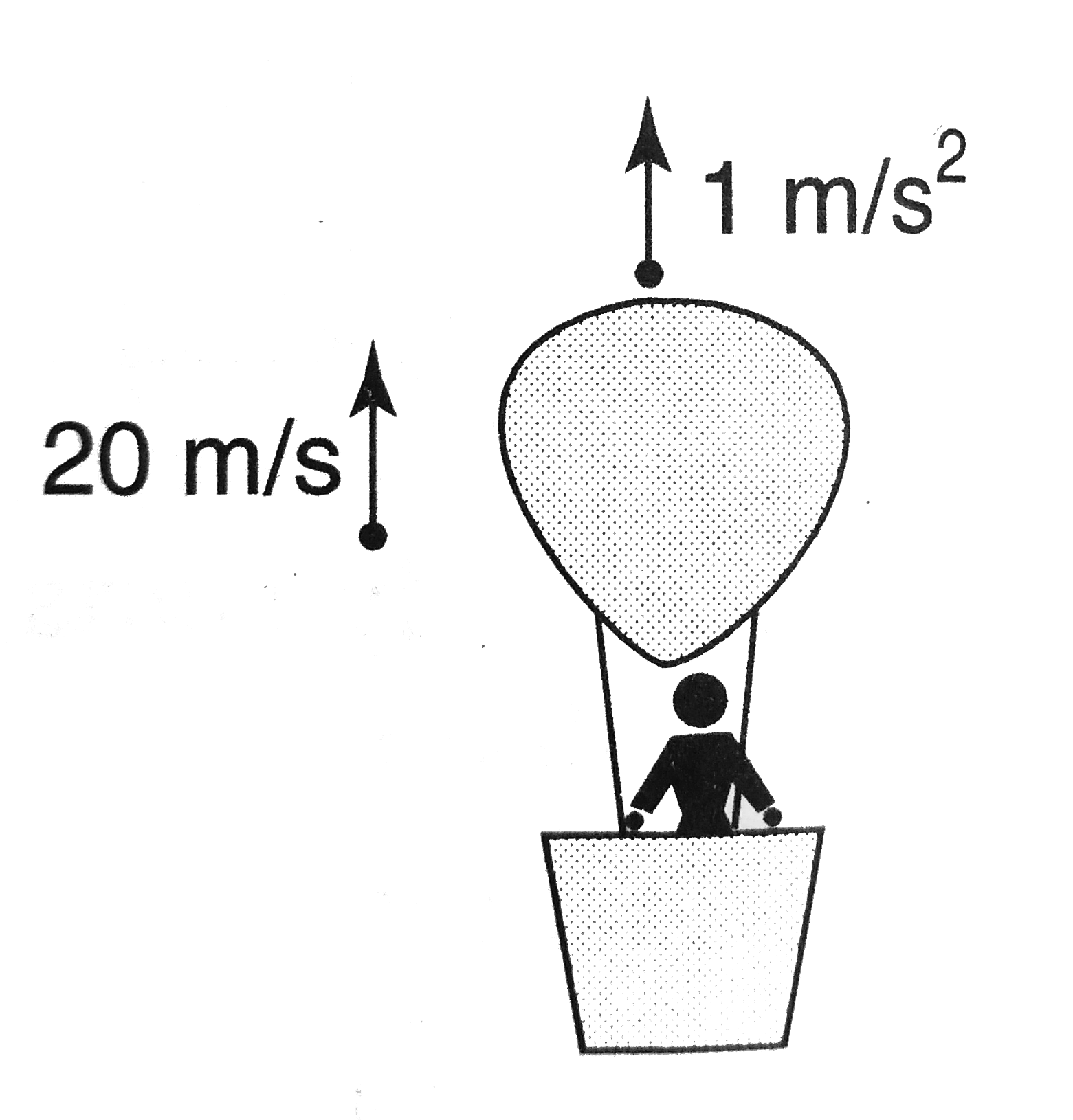
View SolutionA train stopping at two stations `2 km` apart on a straight line takes `4` minutes for the journey. Assuming that its motion its uniformly accelerated and then unoformly retarded. If `(1)/(x)+(1)/(y) = n`, where 'x' and 'y' are the magnitudesof the acceleration and retardation respectively. find the value of `n`.
View SolutionA point moves with uniform acceleration and `v_(1), v_(2)`, and `v_(3)` denote the average velocities in the three successive intervals of time `t_(1).t_(2)`, and `t_(3)` Which of the following Relations is correct?.
View SolutionA parachutist drops first freely from a plane for `10 s` and then his parachute opens out. Now he descends with a net retardation of `2.5 ms^(-2)` If he bail out of the plane at a height of `2495 m` and `g=10 ms^(-2)`, his velocity on reaching the ground will be`.
View SolutionThree particles starts from origin at the same time with a velocity `2 ms^-1` along positive x-axis, the second with a velocity `6 ms^-1` along negative y-axis, Find the velocity of the third particle along `x = y` line so that the three particles may always lie in a straight line.
View SolutionA lift performs the first part of ascent with uniform acceleration `a` and the remainder with uniform retardation `2a`. The lift starts from rest and finally comes to rest. If `t` is the time of ascent. Find the height ascended by lift.
View SolutionA particle is projected upwards from the top of a tower. Treat point of projection as origin and upwards as positive. Consider three point on its path such that at (`s` represents displacement from origin and `v` represents velocity).
(i) `s gt 0, v gt 0`
(ii) `s gt 0, v lt 0`
(iii) `x lt 0, v lt 0`
Which of the following correctly indicates the distance travelled by particle since its projection to respective points in apalphariate order ?
View SolutionTwo car `A` and `B` travelling in the same direction with velocities `v_1` and `v_2(v_1 gt v_2)`. When the car `A` is at a distance `d` ahead of the car `B`, the driver of the car `A` applied the brake producing a uniform retardation `a`. There wil be no collision when.
View SolutionA railway track runs parallel to a road until a turn brings the road to railway crossing. A cyclist rides along the road every day at a constant speed `20 km//hr`. He normally meets a train that travels in same direction at the crossing. One day he was late by `25` minutes and met the train `10 km` before the railway crossing. Find the speed of the train.
View SolutionTwo particles `P` and `Q` start from rest and move for equal time on a straight line. Particle `P` has an acceleration of `X m//s^2` for the first half of the total time and `2 X m//s^2` for the second half. The particle `Q` has an acceleration of `2 X m//s^2` for the first half of the total time and `X m//s^2` for the second half. Which particle has covered longer distance ?
View SolutionAn insect moving along a straight line, travels in every second distance equal to the magnitude of time elapsed. Assuming acceeleration to be constant, and the insect starts at `t = 0`. Find the magnitude of initial velocity of insect.
View SolutionA car starts from rest and moves with uniform acceleration a on a straight road from time `t=0` to `t=T`. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
View SolutionThe acceleration of particle is increasing linearly with time `t` as `bt`. The particle starts from the origin with an initial velocity `v_0`. The distance travelled by the particle in time `t` will be.
View SolutionA stone is dropped from the top of a tower. When it crosses a point 5 m below the top, another stone is let fall from a point 25 m below the top. Both stones reach the bottom of the tower simultaneously. Find the height of the tower. Take `g = 10 m//s^2.`
View SolutionA car , starting from rest, accelerates at the rate `f` through a distance `S` then continues at constant speed for time `t` and then decelerates at the rate `(f)/(2)` to come to rest . If the total distance traversed is `15 S` , then
View SolutionParticle beginning from rest, travels a distance `S` with uniform acceleration and immediately after travels a distane of `3 S` with uniform velocity followed by a distance `5 S` with uniform deceleration, and comes to rest. Then the ratio of average speed to the maximum speed of the particle is.
View SolutionA car moving at `160 km//h` when passes the mark-A, driver applies brake and reduces its speed uniformly to `40 km//h` at mark-C. The mark are spaced at equal distances along the road as shown below.
At which part of the track the car has instantaneous speed of `100 km//h` ? Neglect the size of the car.

View SolutionA body travelling with uniform acceleration crosses two point `A` and `B` with velocities `20 m s^-1` and `30 m s^-1` respectively. The speed of the body at the mid-point of `A` and `B` is.
View SolutionA particle moving with uniform acceleration along x-axis has speed `v m//s` at a position `x` metre given `v = sqrt(180 - 16 x)" "(0 lt x lt(180)/(16))`
The acceleration of the particle in `m//s^2` is.
View SolutionThe velocity of a particle moving in a straight line varies with time in such a manner that `v` versus `t` graph is represented by one-half of an ellipse. The maximum velocity is `v_m` and the total time of motion is `t_0`
(i) average velocity of the particle is `(pi)/(4) v_m`
(ii) such motion cannot be realized in practical terms.
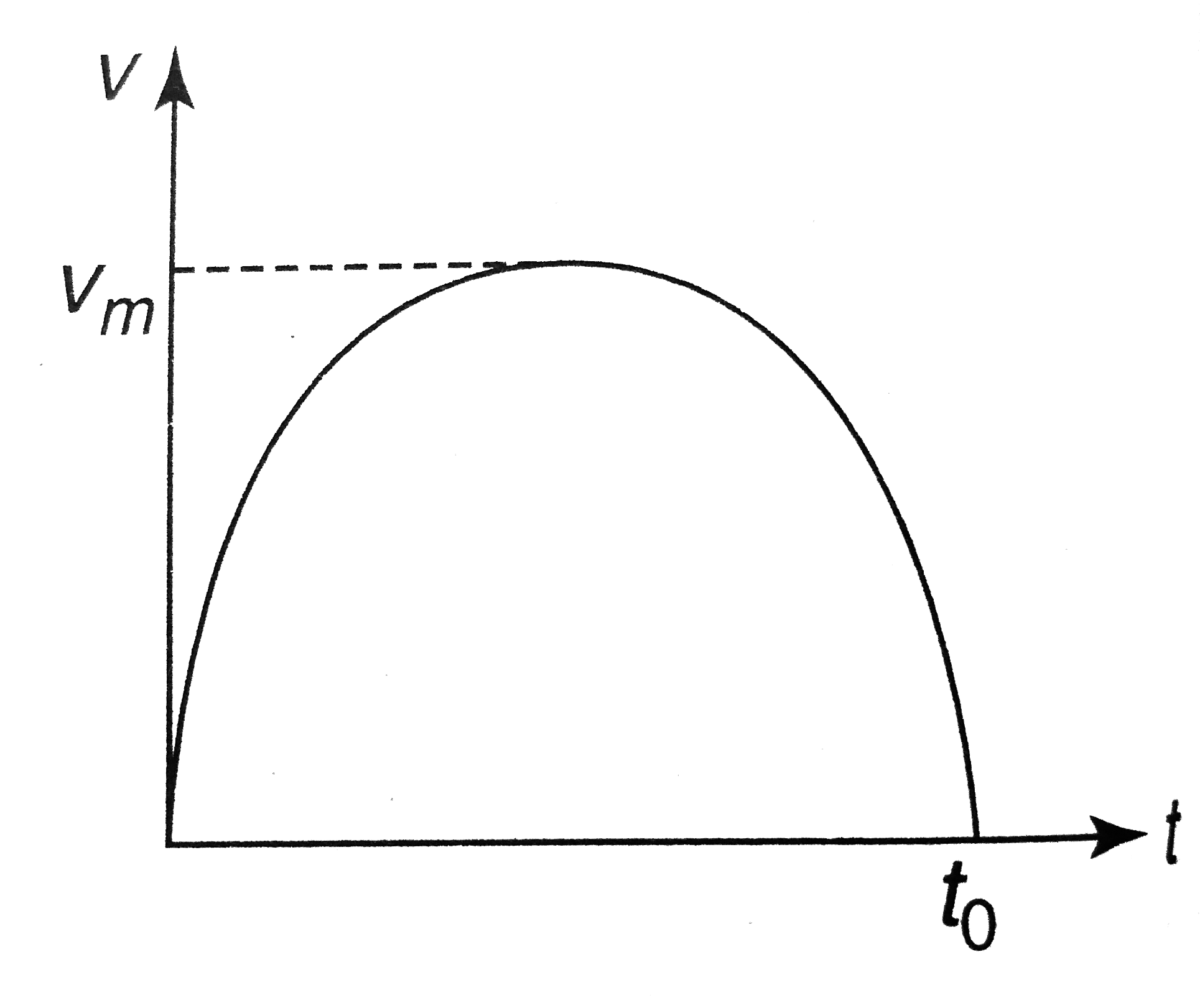
View SolutionA ball is dropped from some height. After rebound from the floor it ascends to the same height. Draw the velocity-time graph for the given motion.
View Solution
Chapter Test questions and complete solutions for chapter GENERAL KINEMATICS AND MOTION IN ONE DIMENSION of A2Z PHYSICS (HINGLISH) of Class 11