Complete Solutions to Integer of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Integer |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
A bullet is fired on a fixed target. It penetrates inside the target through distance `d = 3.75 cm` and then stops. mass of the bullet is `m = 1 kg` and of the target is `M = 4 kg`. Now an identical bullet moving with the same velocity is fired on the identical target which is placed at rest on a frictionless horizontal surface. Then find the distance (in cm) to which the bullet will penetrate inside the target?
View SolutionA frog sits on the end pf a long boord of length L. the boord rests on a fricationless horizontal table. The frog wants os the minimum takes - off speed i.e relative to ground v that allows the frog yo do the trick? The board and the frog have equal masses.
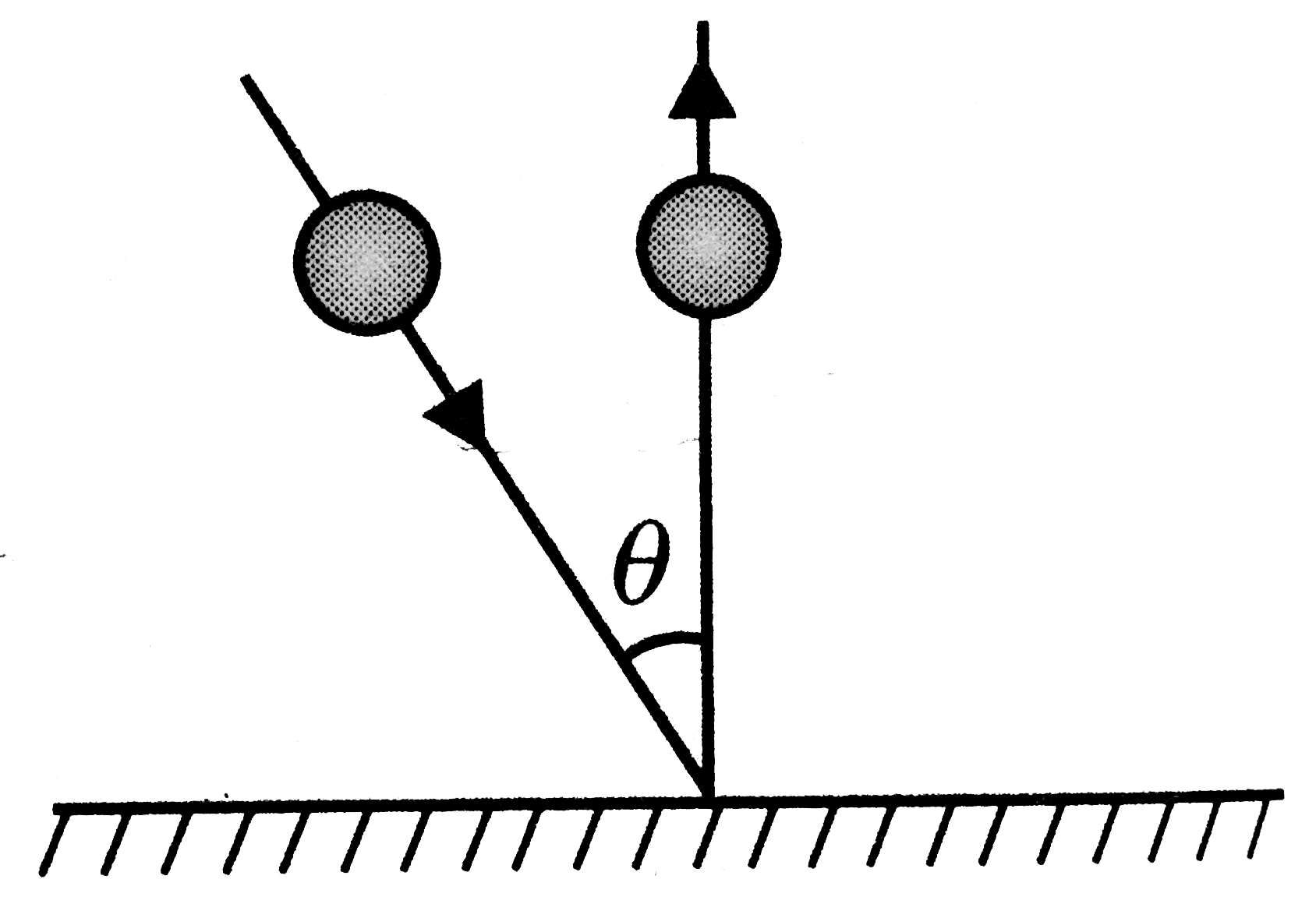
View SolutionA ball of mass `1 kg` moving with a velocity of `5 m//s` collides elastically with rough ground at an angle `theta` with the vertical as shown in Fig. What can be the minimum coefficient of friction if ball rebounds vertically after collision? (given `tantheta=2`)
View SolutionA small sphere of mass `m =1 kg` is moving with a velocity `(4hati-hatj) m//s`. it hits a fixed smooth wall and rebounds with velocity `(hati + 3hatj) m//s`. The coefficient of restitution between the sphere and the wall is `n//16`. Find the value of `n`.
View SolutionA child of mass `4 kg` jumps from cart `B` to cart A and then immediately back to cart `B`. The mass of each cart is `20 kg` and they are initially at rest. In both the cases the child jumps at `6 m//s` relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of `V_(B)` and `V_(A)`, respectively, find the ratio of `6V_(B)` and `5V_(A)`.

View SolutionA man of mass `M = 58 kg` jumps from an airplane as shown in Fig. He sees the hard ground below him and a lake at a distance `d = 1 m` from the point directly below him. He immediately puts off his jacket (mass `m = 2` kg) and throws it in a direction directly away from the lake. If he just fails to strike the ground, find the distance (in `10^(1) m`) he should walk now to pick his jacket. (Neglect air resistance and take the velocity of man at the time of jump with respect to earth zero.)

View SolutionA ball of mass `m` makes head-on elastic collision with a ball of mass urn which is initially at rest. Show that the fractional transfer of energy by the first ball is `4n/(1 + n)^(2)`. Deduce the value of `n` for which the transfer is maximum.
View SolutionA massless spring of force constant `1000 Nm^(-1)` is compressed a distance of `20 cm` between discs of `8 kg` and `2 kg`, spring is not attached to discs. The system is given an initial velocity `3 ms^(-1)` perpendicular to length of spring as shown in the figure. What is ground frame velocity of `2 kg` block (in `ms^(-1)`) when spring regains its natural length.

View SolutionFigure shows position and velocities of two particles moving under mutual gravitational attraction in space at time `t = 0`. The position of centre of mass after one second is (in meters)
.

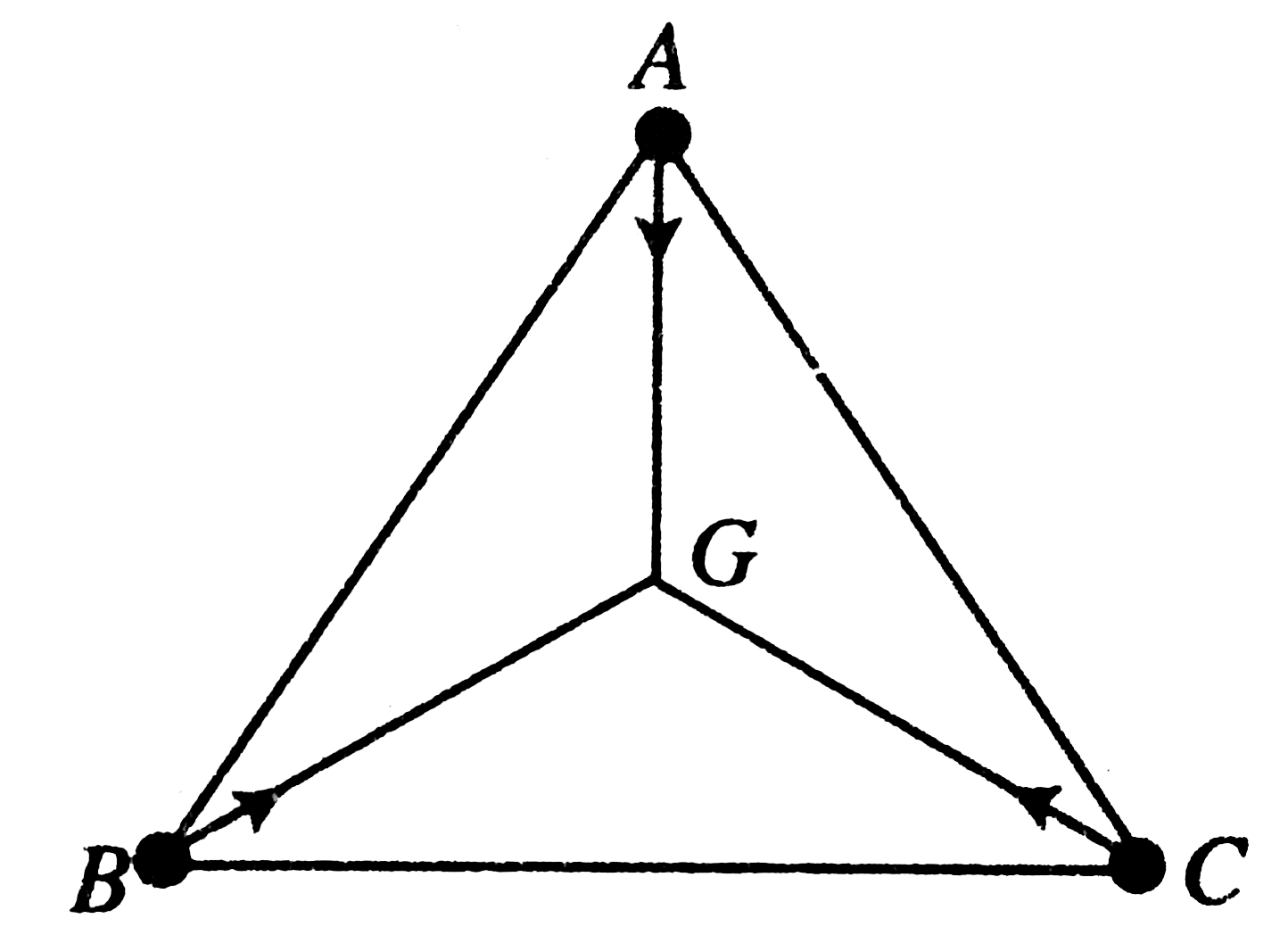
View SolutionThree particles` A, B` and `C` of equal mass move with equal speed `V = 5 ms^(-1)` along the medians of an equilateral triangle as shown in the figure. They collide at the centroid `G` of the triangle. After the collision, `A` comes to rest, `B` retraces its path with the speed `V = 5 ms^(-1)`. What is the speed of `C`?
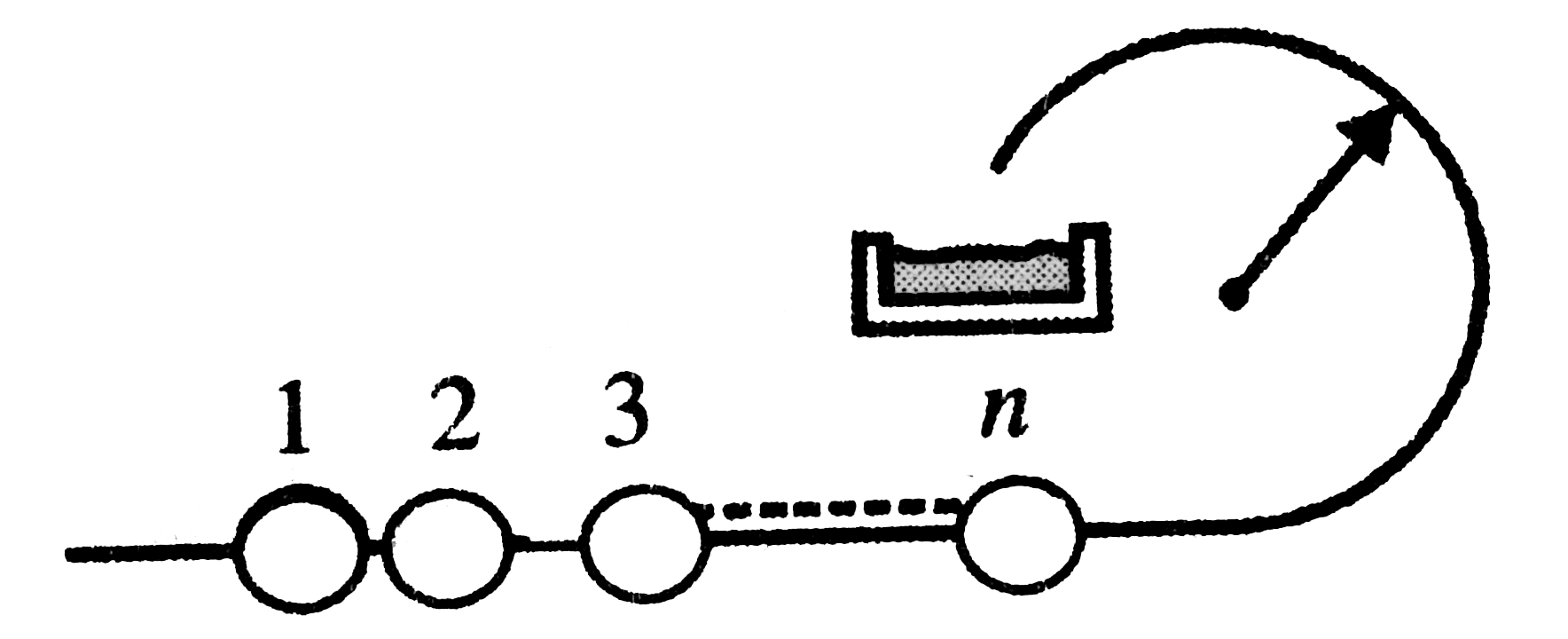
View Solution`N` beads identical beads are resting on a smooth horizontal wire which is circular at the end with radius `r = 0.5 m` as shown in the figure. Find the minimum velocity which should be imparted to the first bead such that `nth` bead will fall in the tank after completing full circle in vertical plane as shown in the figure. Take all the collisions between the beads elastic `(e = 1)`.
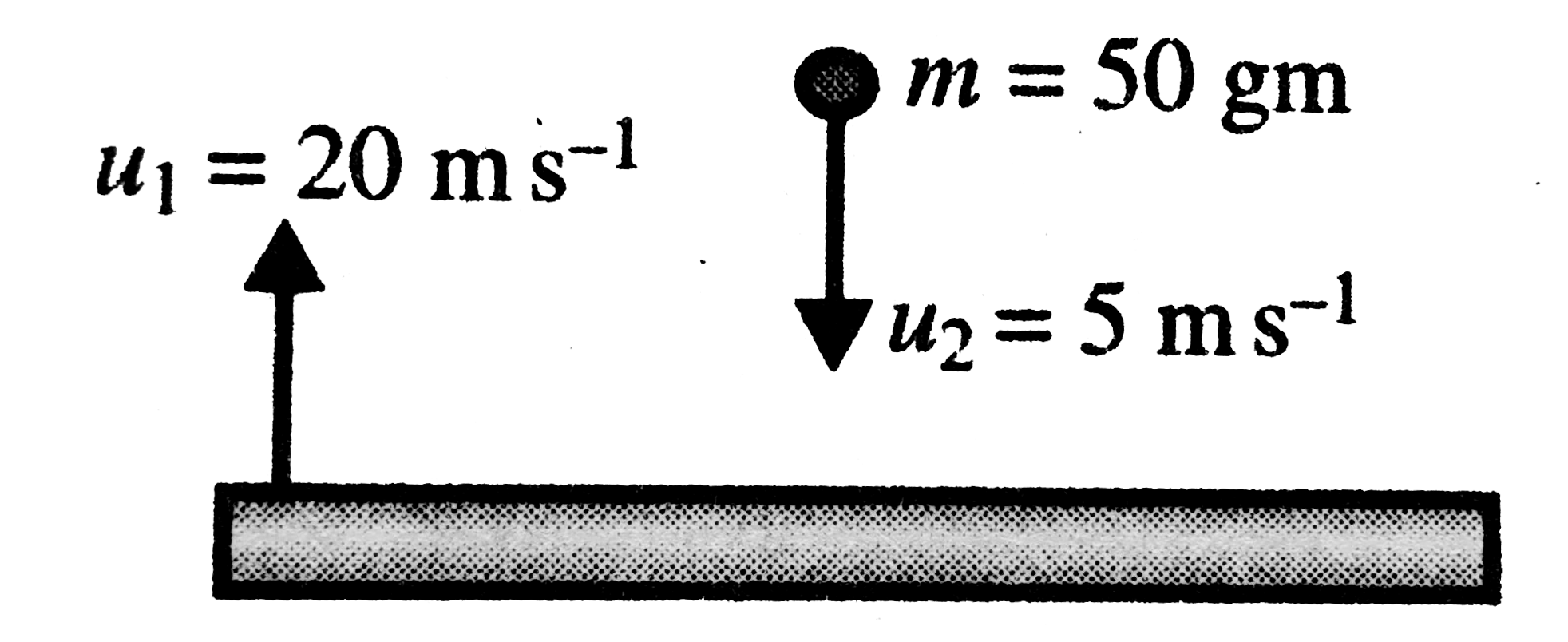
View SolutionAn elevator platform is going up at a speed `20 ms^(-1)` and during its upward motion a small ball of `50 g` mass falling in downward direction strikes the platform elastically at a speed `5 ms^(-1)`. Find the speed (in `ms^(-1)`) with which the ball rebounds.
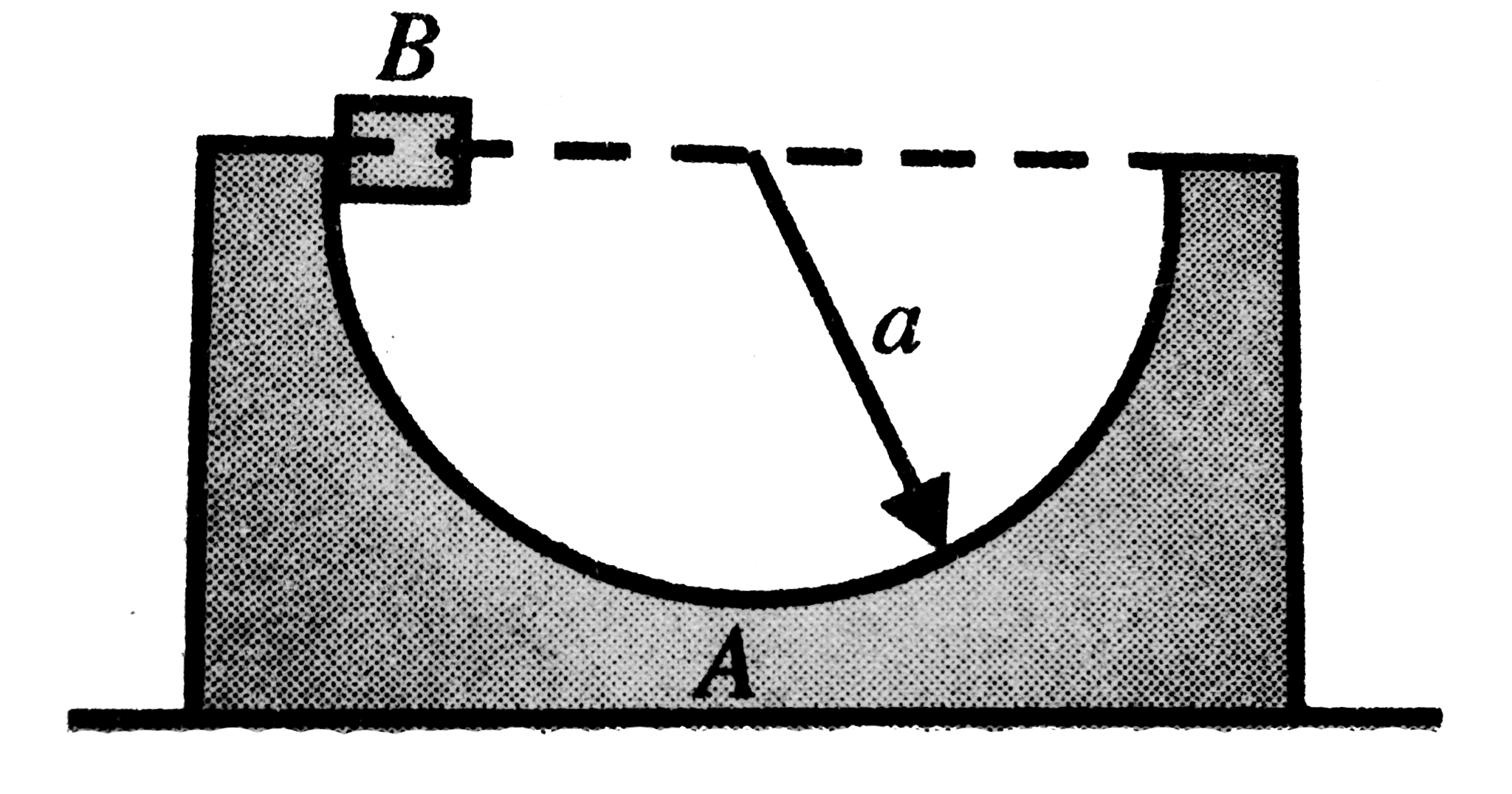
View SolutionFigure shows a wedge `A` of mass `6 m` smooth semicircular groove of radius `a= 8.4 m` placed on a smooth horizontal surface. A small block `B` of mass `m` is released from a position in groove where its radius is horizontal. Find the speed (in `ms^(-1)`) of bigger block when smaller block reaches its bottommost position.
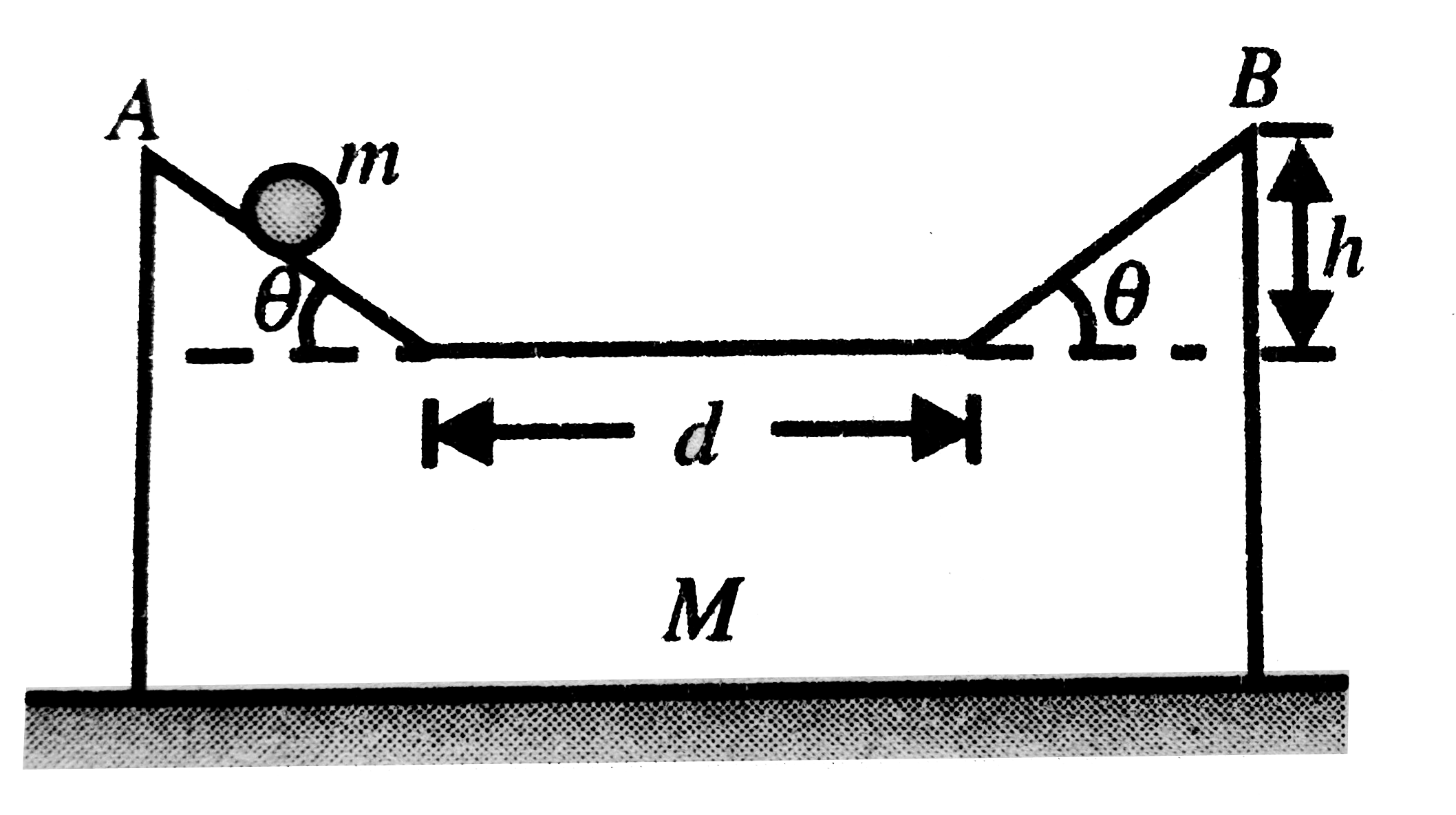
View SolutionA ball of mass `m` is allowed to roll down the wedge of mass `M = 2m` as shown in the figure. What is the displacement of wedge (in `m`) when the ball reaches from `A` to `B`? Take `theta=45^(@), h=1m, d=4m`
View SolutionA railway flat car, whose mass together with the artillery gun is `M = 2 m`, moves at a speed `V`. The gun barrel makes an angle `alpha = 60^(@)` with the horizontal. A shell of mass `m` leaves the barrel at a speed `v = 12 ms^(-1)`, relative to the barrel. Find the speed of the flat car `V` (in `ms^(-1)`) in order that it may stop after the firing.
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View Solution
Integer questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11