Complete Solutions to Exercise 1.2 of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Exercise 1.2 |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
A bomb, initially at rest, explodes into several pieces. (a) Is linear momentum of the system conserved? (b) Is kinetic energy of the system conserved? Explain.
01:43View SolutionYou are standing perfectly still and then you take a step forward. Before the step your momentum was zero, but afterward you have some momentum. Is the principle of conservation of momentum violated in this case?
02:00View SolutionDoes the centre of mass of a rocket in free space accelerate? Explain. Can the speed of a rocket exceed the exhaust speed of the fuel? Explain.
02:11View SolutionDiscuss the possibility of conservation of linear momentum of a block moving on a rough inclined plane if `mu=tantheta`
 01:39View Solution
01:39View SolutionA shell is fired from a cannon with a speed of `100 m//s` at an angle `30^(@)`with the vertical (`y`-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio `1:2`. The lighter fragment moves vertically upwards with an initial speed of `200 m//s`. What is the speed of the heavier fragment at the time of explosion?
07:15View SolutionFigure shows a block `A` of mass `6 m` having a smooth semicircular groove of radius `a` placed on a smooth horizontal surface. A block `B` of mass `m` is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
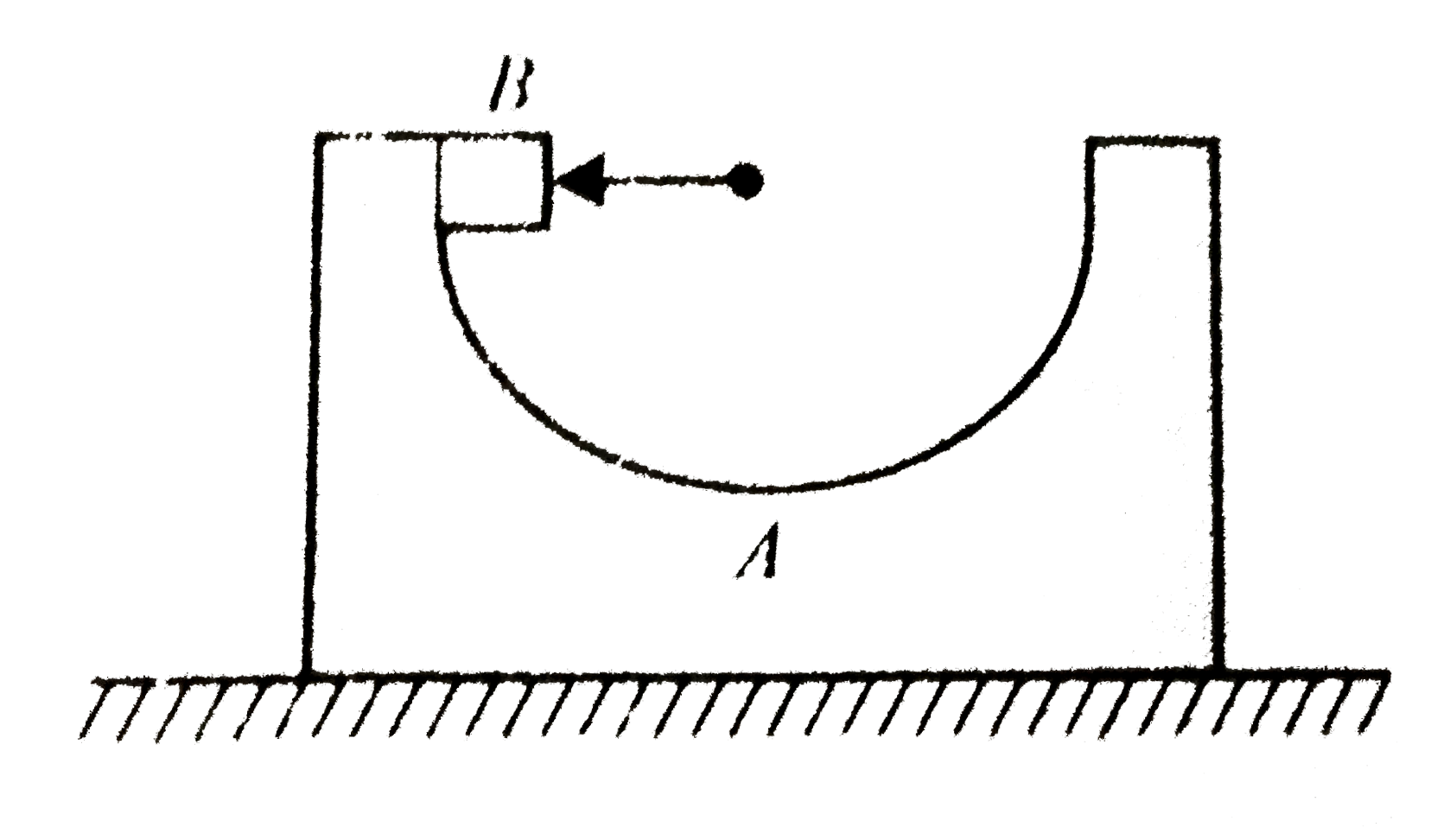 04:01View Solution
04:01View SolutionTwo friends `A` and `B` (each weighing `40 kg`) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass `4 kg` on the platform towards `B` which `B` catches. Then `B` rolls the ball towards `A` and `A` catches it. The ball keeps on moving back and forth between `A` and `B`. The ball has a fixed speed of `5 m//s` on the platform.
a. Find the speed of `A` after he rolls the ball for the first time.
b. Find the speed of `A` after he catches the ball for the first time.
c. Find the speed of `A` and `B` after the ball has made five round trips and is held by `A`.
d. How many times can `A` roll the ball?
e. Where is the centre of mass of the system `A + B +` ball at. the end of the nth trip?View SolutionA smooth wedge of mass `M` rests on a smooth horizontal surface. A block of mass `m` is projected from its lowermost point with velocity `v_(0)`. What is the maximum height reached by the block?
 03:41View Solution
03:41View SolutionTwo identical buggies `1` and `2` with one man in each move along parallel rails. When the buggies are opposite to each other, the men jump in a direction perpendicular to the direction of motion of buggies, so as to exchange their places. As a consequence, buggy `1` stops and buggy `2` keeps moving in the same direction with its final velocity `v`. Find the initial velocities `v_(1)` and `v_(2)` of buggies. Mass of each buggy (without man) equals `M` mass of each man is ignore frictional effects anywhere and the buggies are constrained to move along the rails only.
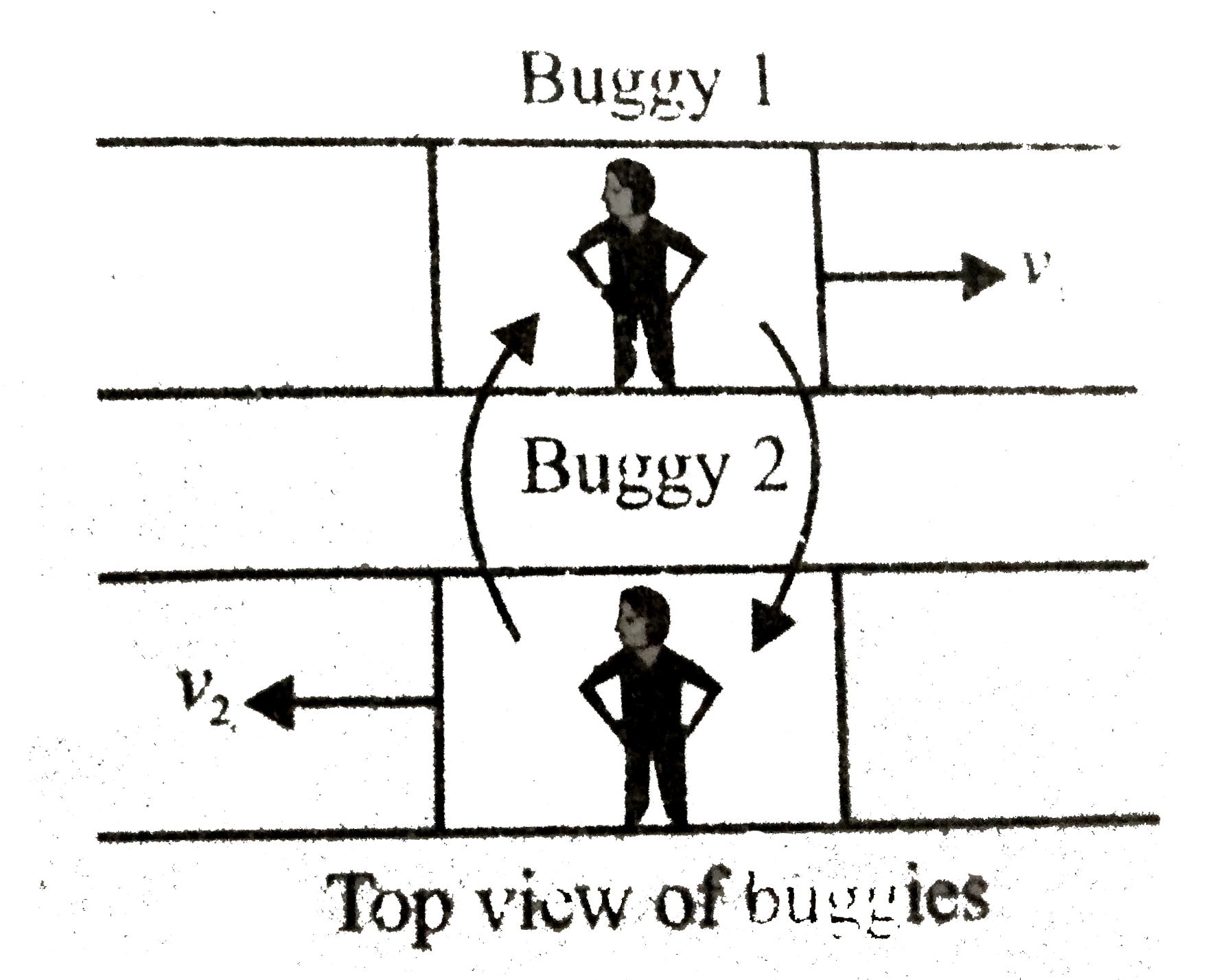 View Solution
View SolutionIn Fig. a man stands on a boat floating in still water. The mass of the man and the boat is `60 kg` and `120 kg`, respectively.

a. If the man walks to the front of the boat and stops. what is the separation between the boat and the pier now?
b. If the man moves at a constant speed of `3 m//s` relative to the boat, what is the total kinetic energy of the system (boat `+` man)? Compare this energy with the kinetic energy of the system if the boat was tied to the pier.View SolutionTwo blocks of masses `m_(1) = 2 kg` and `m_(2) = 5` kg are moving in the same direction along a frictionless surface with speeds `10 m//s` and `3 m//s`, respectively, `m_(2)` being ahead of `m_(1)`. An ideal spring with `k = 1120 N//m` is attached to the back side of `m_(2)`. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
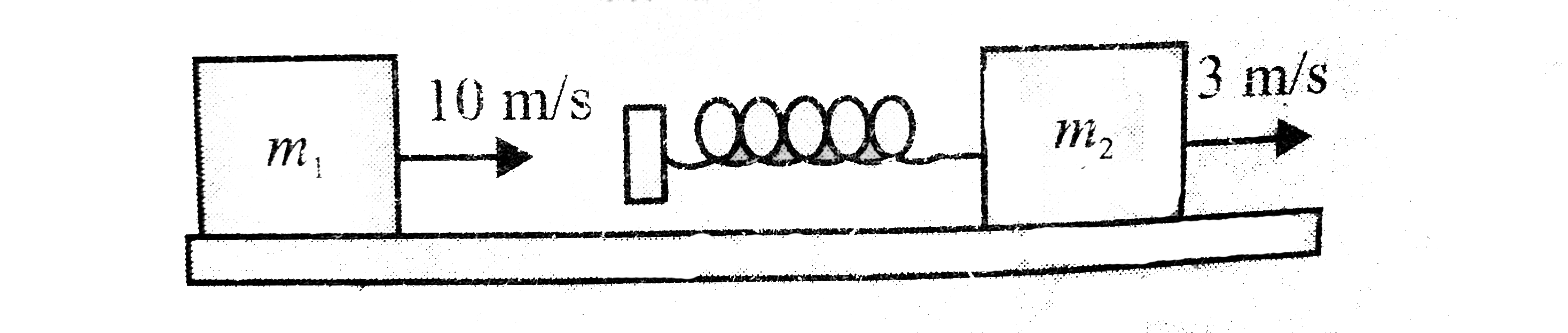 View Solution
View SolutionAn `80 kg` boy and his `40 kg` sister, both wearing roller blades, face each other at rest. The girl pushes the boy hard, sending him backward with velocity `3.0 m//s` towards the west. Ignore friction, (a) Describe the subsequent motion of the girl. (b) How much chemical energy is converted into mechanical energy in the girl's muscles? (c) Is the momentum of the boy-girl system conserved in the pushing apart process? How can it he with no motion beforehand and plenty of motion afterward?
03:38View SolutionTwo blocks of masses `M` and `3M` are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass `3M` moves to the right with a speed of `2.00 m//s`. (a) What is the velocity of the block of mass `M`. (b) Find the system's original elastic potential energy, taking `M = 0.350 kg`. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
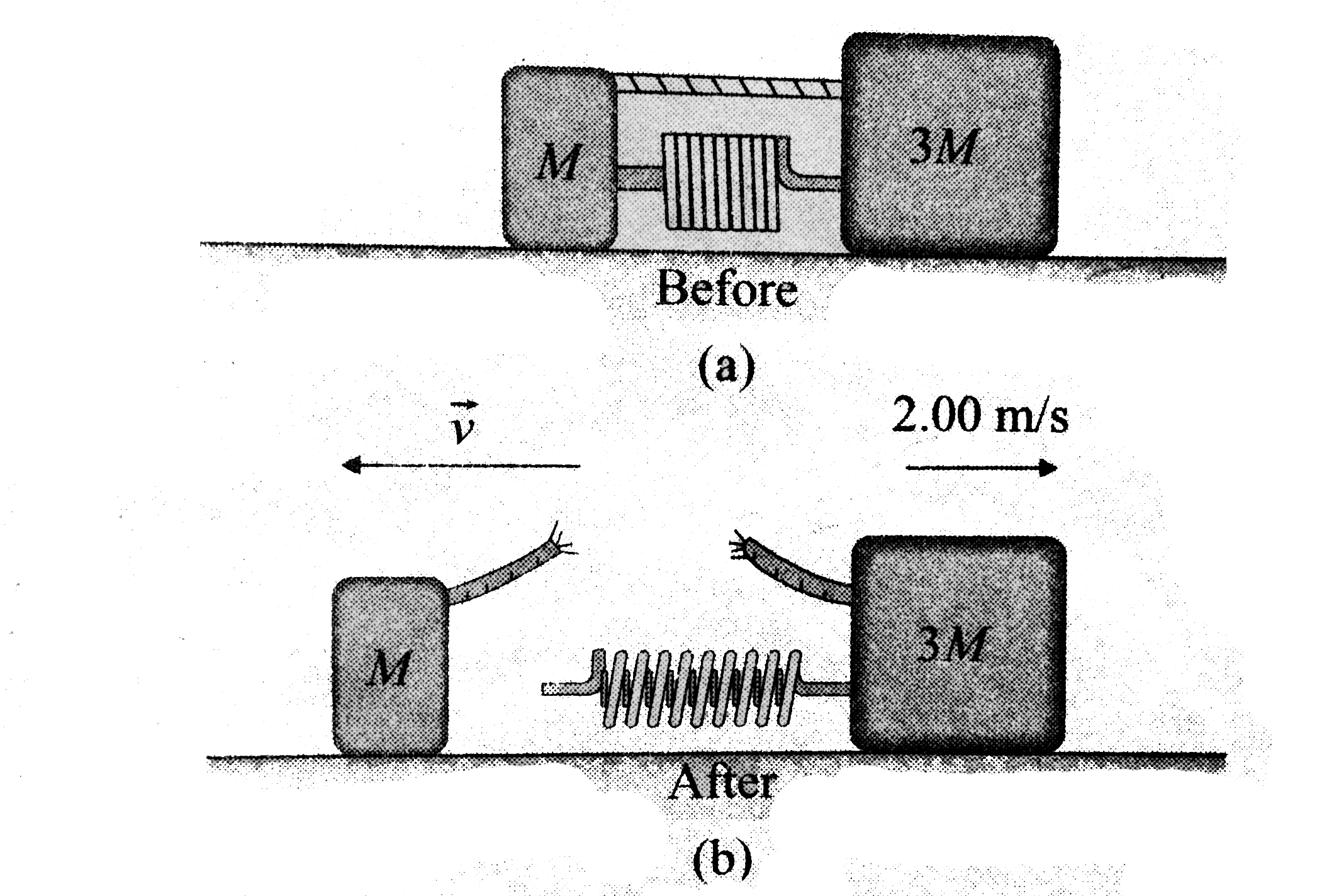 View Solution
View SolutionA pendulum bob of mass `10^-2kg` is raised to a height `5xx10^-2m` and then released. At the bottom of its swing, it picks up a mass `10^-3kg`. To what height will the combined mass rise?
06:38View SolutionA rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface and fires 10 shots horizontally. Each bullet has a mass 10 g and a muzzle velocity of 800 `ms^(-1)` . The velocity which the rifle man attains after firing 10 shots is
05:47View SolutionA projectile of mass `50 kg` is shot vertically upwards with an initial velocity of `100 m//s`. After `5 s`, it explodes into two fragments, one of which having a mass of `20 kg` travels vertically up with a velocity of `150 m//s`:
a. What is the velocity of the other fragment that instant?
b. Calculate the sum of momentum of fragment `3s` after the explosion. What would have been the momentum of the projectile at this instant if there had hem explosion?04:55View Solutiona. A rail road flat car of mass `M` can roll without friction along a straight horizontal track . Initially, a man of mass `m` is standing on the car which is moving to the right with speed `v_(0)`. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is `v_(rel)` just before he jumps off at the left end?
b. If there are `n` men each of mass `m` on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?
 05:28View Solution
05:28View Solutiona. A rail road car of mass M is moving without friction on a straight horizontal track with a velocity ct. A man of mass m lands on it normally from a helicopter. What will be the new velocity of the car? ltbgt b. If now the man begins to run on it with speed um with respect to car in a direction opposite to motion of the car, what will be the new velocity of the car?
01:39View SolutionA shell of mass `2 kg` moving at a rate of `4 m//s` suddenly explodes into two equal fragments. The fragments go in directions inclined with the original line of motion with equal velocities, If the explosion imparts `48 J` of translational kinetic energy to the fragments, find the velocity and direction of each fragment.
View SolutionA mud ball at rest explodes into three fragmennts of masses in the ragio `1:2:1`. the two equal masses move with velocities `2hati+5hatj-6hatk` and `-4hati+3hatj+2hatk`. Find the velocity of the find mass.
 01:55View Solution
01:55View SolutionA hemisphere of radius `R` and of mass `4m` is free to Slide with its base on a smooth horizontal table. A particle mass `m` is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement `theta` when velocity of hemisphere has become `v`.
 View Solution
View SolutionA gun (mass `= M`) fires a bullet (mass `= m`) with speed `v_(r)` relative to barrel of the gun which is inclined at an angle of `60^(@)` with horizontal. The gun is placed over a smooth horizontal surface. Find the recoil speed of gun.
 View Solution
View SolutionTwo trolleys `A` and `B` are free to move on a level frictionless track, and are initially stationary. A man on trolley `A` throws a bag of mass `10 kg` with a horizontal velocity of `4 ms^(-1)` with respect to himself on to trolley `B` of mass `100 kg`. The combined mass of trolley `A` (excluding bag) and the man is `140 km`. Find the ratio of velocities of trolleys `A` and `B`, just after the bag lands on trolley `B`.
View Solution
Exercise 1.2 questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11
