Complete Solutions to Subjective of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Two identical smooth balls are projected from points `O` and `A` on the horizontal ground with same speed of projection. The angle of projection in each case is `30^(@)`.The distance between `O` and `A` is `100 m`. The balls collide in mid-air and return to their respective points of projection. If the coefficient of restitution is `0.7`, find the speed of projection of either ball (in `m//s`) correct to nearest integer. (Take `g = 10 ms^(-2)` and `sqrt(3)=1.7)`
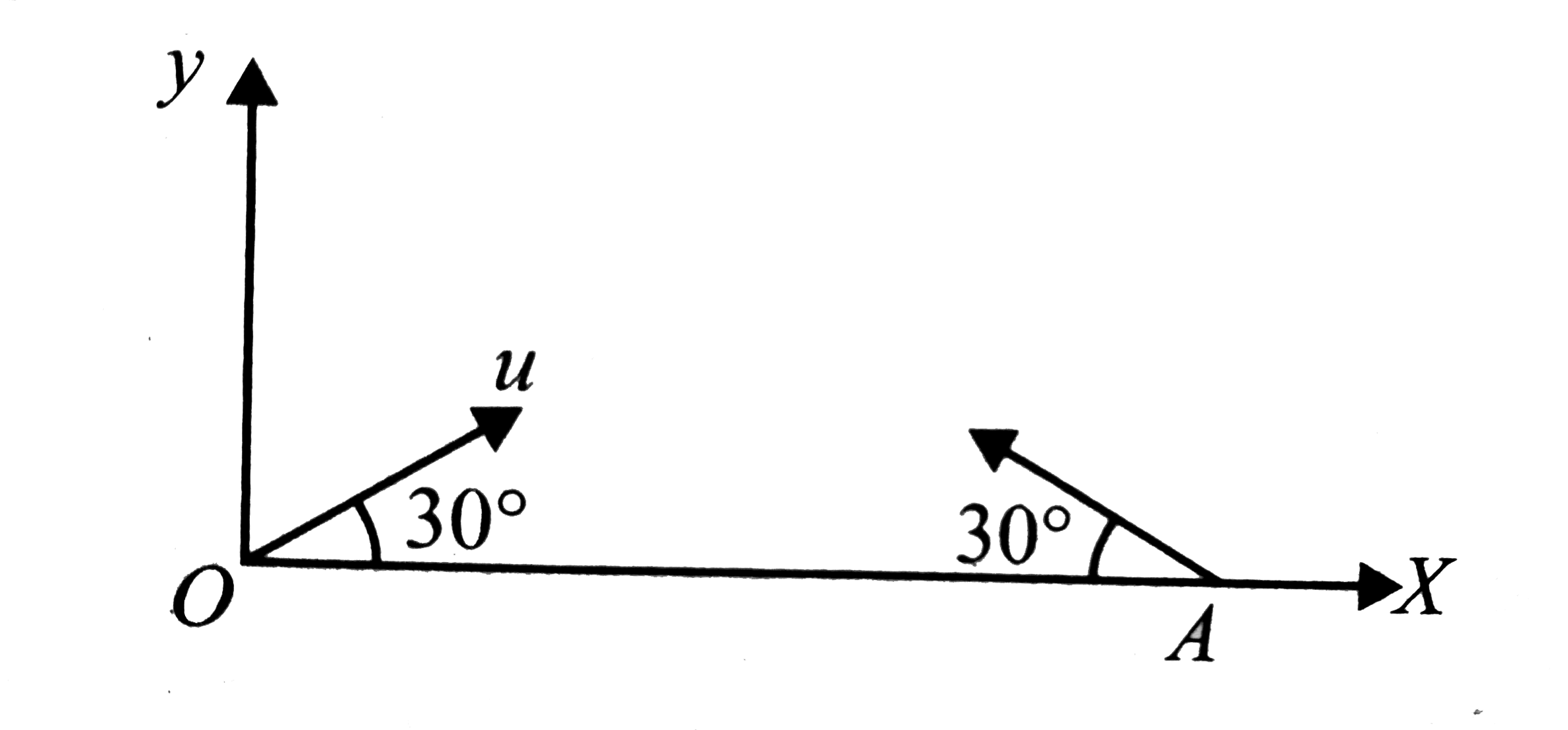 View Solution
View SolutionA stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass `M`. Mass of the man is `m`. initially, the centre of mass of the counterweight is at a height `h` from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
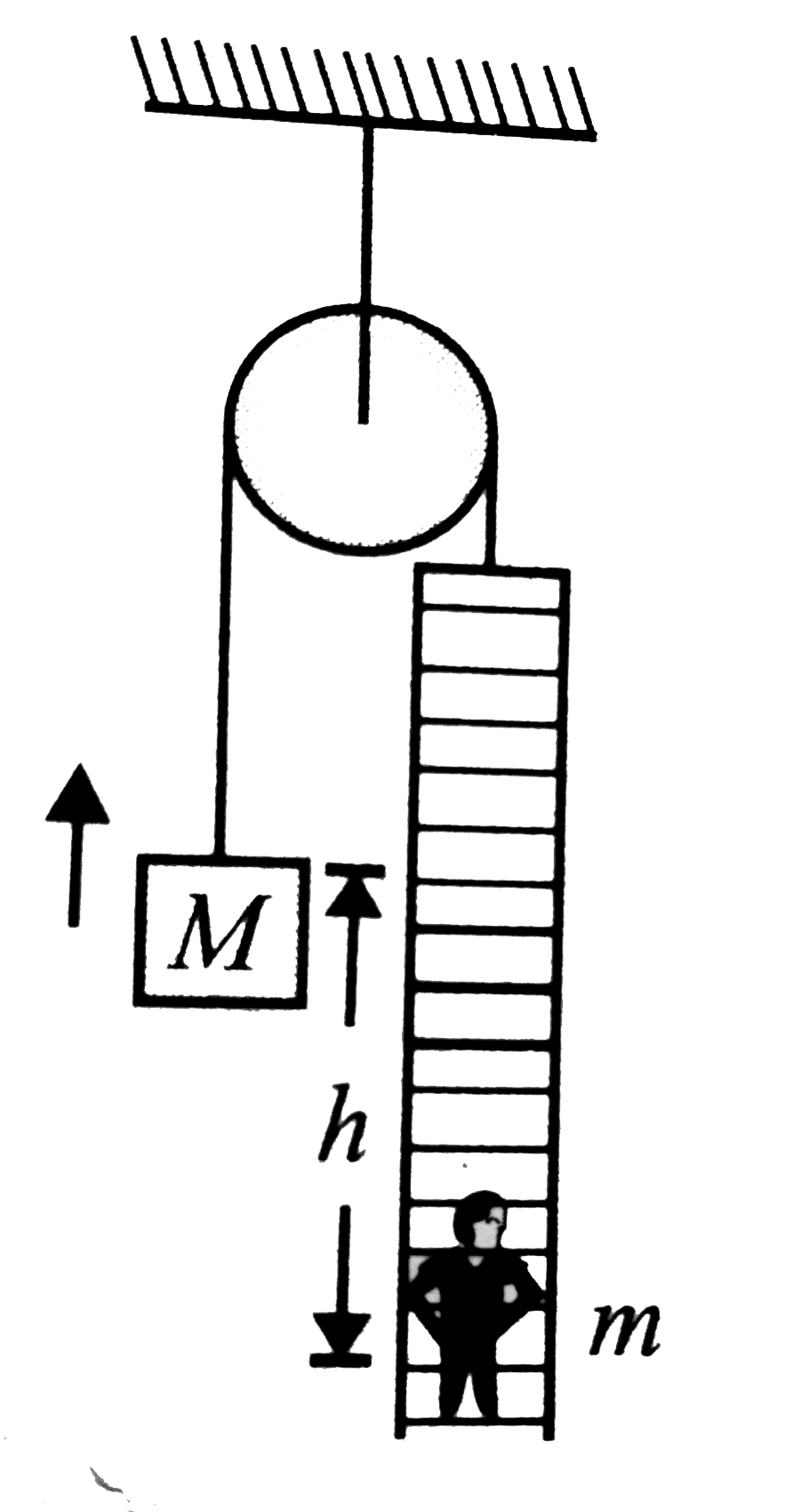 View Solution
View SolutionTwo blocks `A` and `B` are joined by means of a slacked string passing over a massless pulley as shown in Figure. The system is released from rest and it becomes taut when `B` falls a distance `0.5 m`.
a. Find the common velocity of the two blocks just after the string becomes taut.
b. Find the magnitude of impulse on the pulley by the clamp during the small interval while string becomes taut.
 View Solution
View SolutionTwo blocks `A` and `B` of masses `m` and `2m`, respectively are connected by a spring of force constant `k`. The masses are moving to the right with uniform velocity `v` each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block `B` collides head on with a third block `C` of mass `m`, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
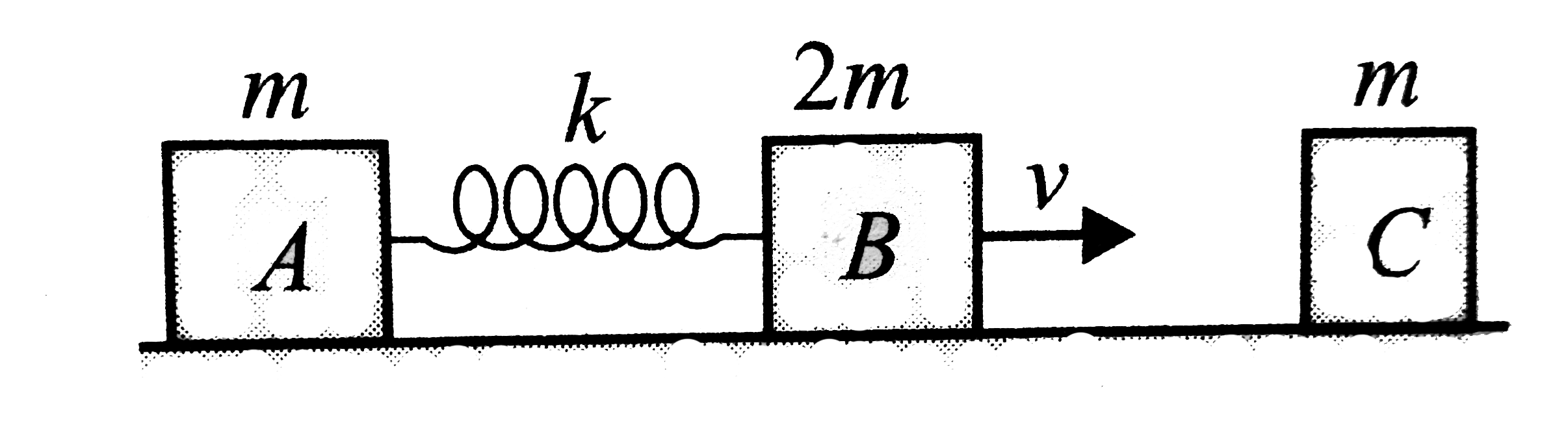 View Solution
View SolutionTwo small spheres `A` and `B` of equal radius but different masses of `3m` and `2m` are moving towards each other and impinge directly. The speeds of `A` and `B` before collision are, respectively, `4u` and `u`. The collision is such that `B` experiences an impulse of magnitude `6mcu`, where `c` is a constant. Determine
a. the coefficient of restitution,
b. the limits for the value of `c` for which such collision is possible.View SolutionFour railroad cars, each of mass `2.50 xx 10^4` kg, are coupled together and coasting along horizontal tracks at speed `v_(I)`towards the south. A very strong movie actor, riding on the second car, uncouples the front car and gives it a big push, increasing its speed to `4.00 m//s` southward. The remaining three cars continue moving south, now at `2.00 m//s`. (a) Find the initial speed of the cars. (b) How much work did the actor do?
02:24View SolutionA particle of mass `m` is made to move with uniform speed `u` along the perimeter of a regular polygon of `n` sides. What is the magnitude of impulse applied by the particle at each corner of the polygon?
04:26View SolutionA smooth ball of mass `1 kg` is projected with velocity `7 m//s` horizontal from a tower of height `3.5 m`. It collides elastically with a wedge of mass 3 kg and inclination of `45^(@)` kept on ground. The ball collides with the wedge at a height of `1 m` above the ground. Find the velocity of the wedge and the ball after collision. (Neglect friction at any contact.)
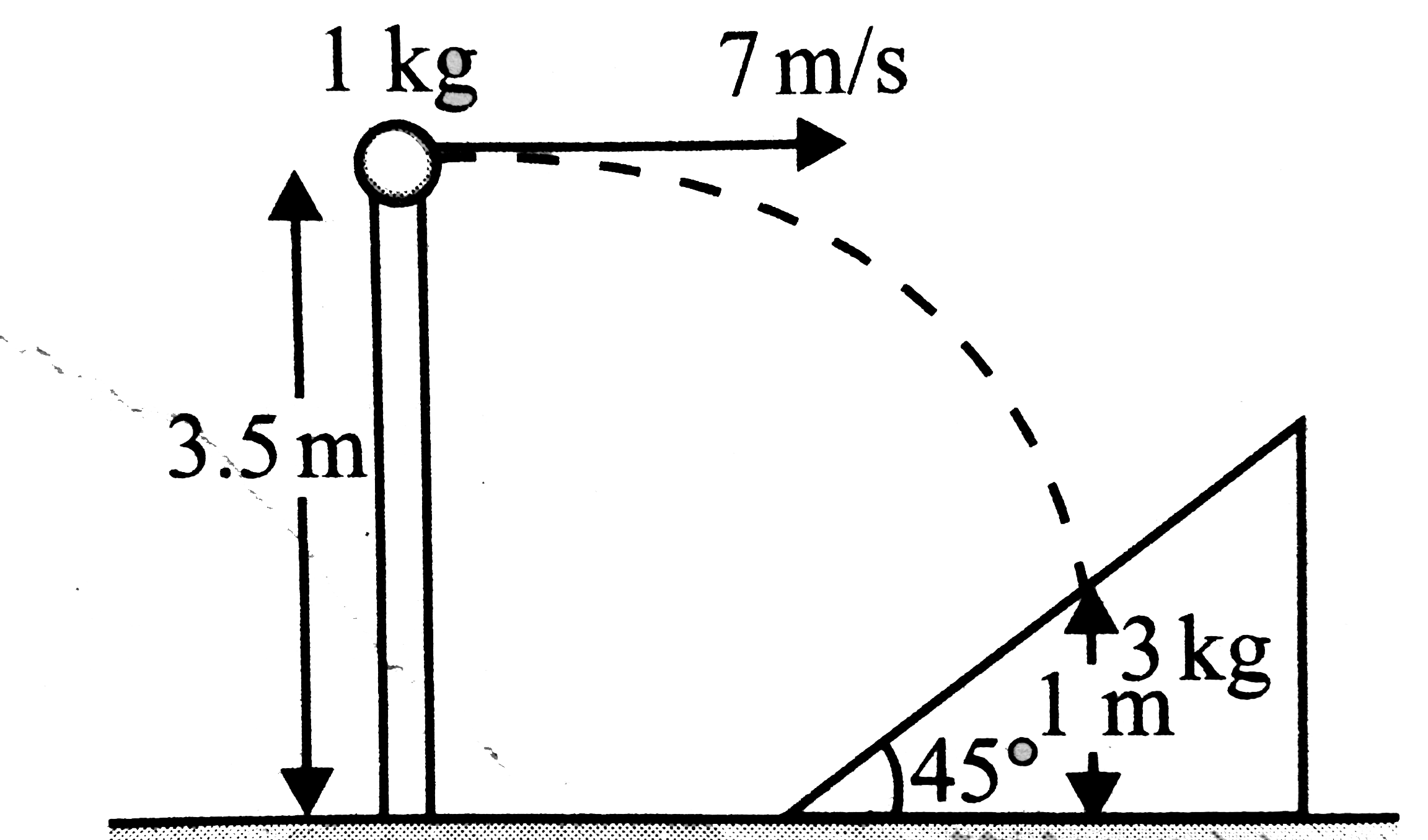 View Solution
View SolutionA small ball is projected from point `P` towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point `P` after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is `n//2`. All surfaces are smooth. Find the value of `n`.
 View Solution
View SolutionA small steel ball `A` is suspended by an inextensible thread of length `l= 1.5 m` from `O`. Another identical ball is thrown vertically downwards such that its surface remains just in contact with thread during downward motion and collides elastically with the suspended ball. If the suspended ball just completes vertical circle after collision, calculate the velocity (in `cm//s`) of the falling ball just before collision `(g = 10 m s^(-2))`.
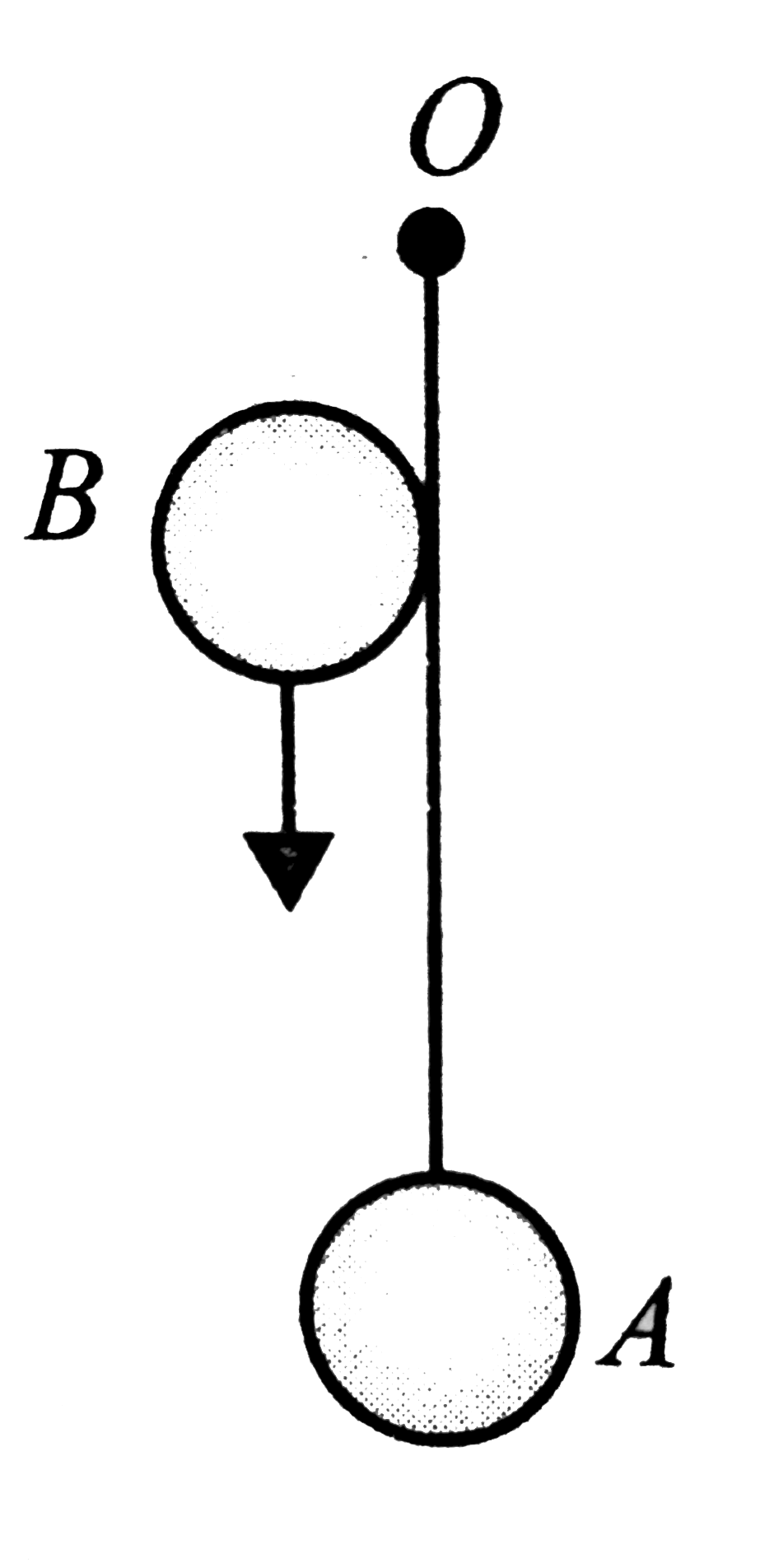 View Solution
View SolutionA tennis ball with (small) mass `m_(2)` rests on the top of a basketball of mass `m_(1)`which is at a height `h` above the ground, and the bottom of the tennis ball is at height `h+ d` above the ground. The balls are dropped. To what height does the tennis ball bounce with respect to ground? (Assume all collisions to be elastic and `m_(1)gt gt m_(2))`
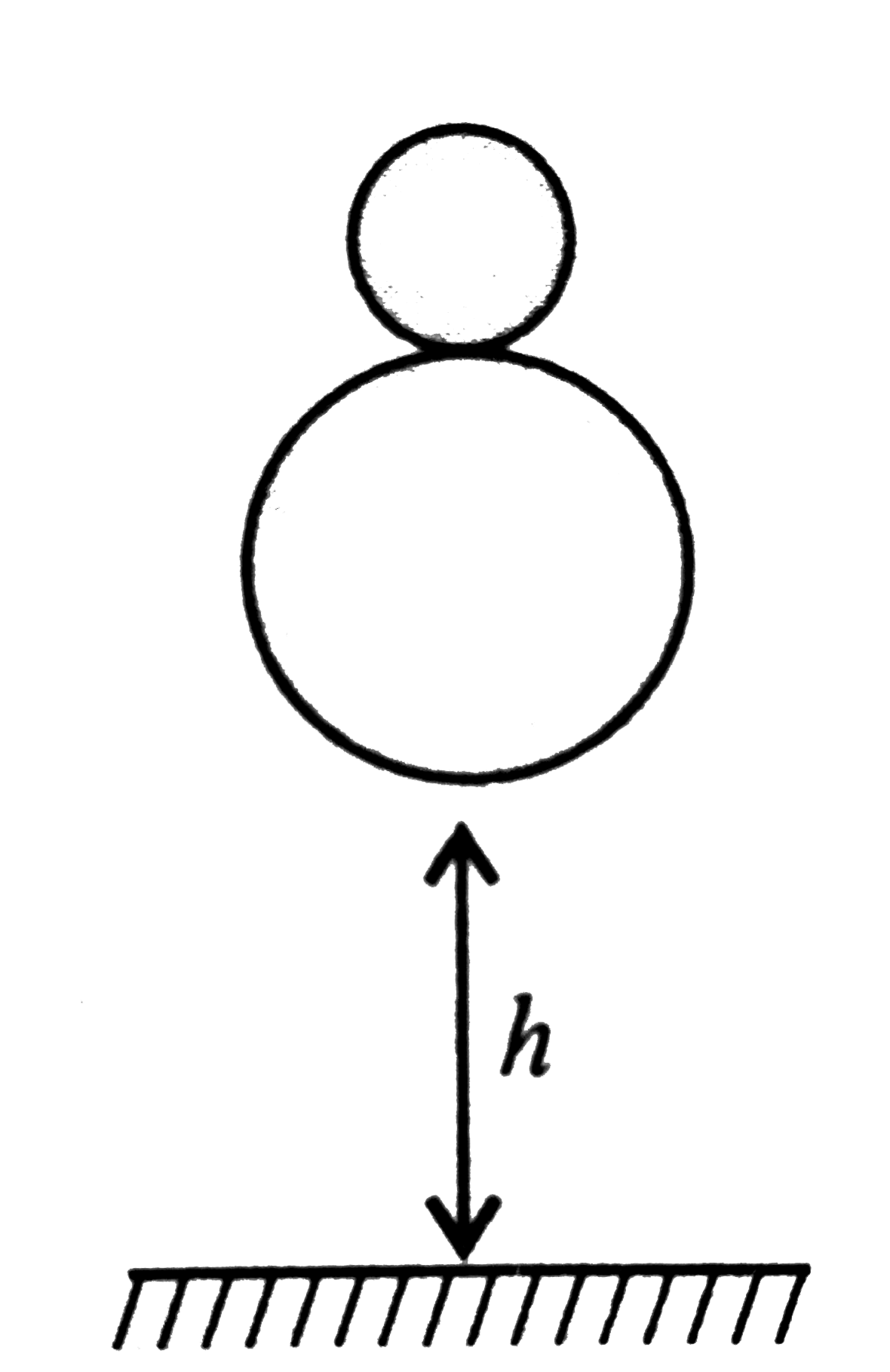 03:29View Solution
03:29View SolutionA ball of mass `m` hits a wedge of mass `M` vertically with speed `u`, which is placed, on a smooth horizontal surface. Find the maximum compression in the spring, if the collision is perfectly elastic and no friction any where. Spring constant of spring is `K`.
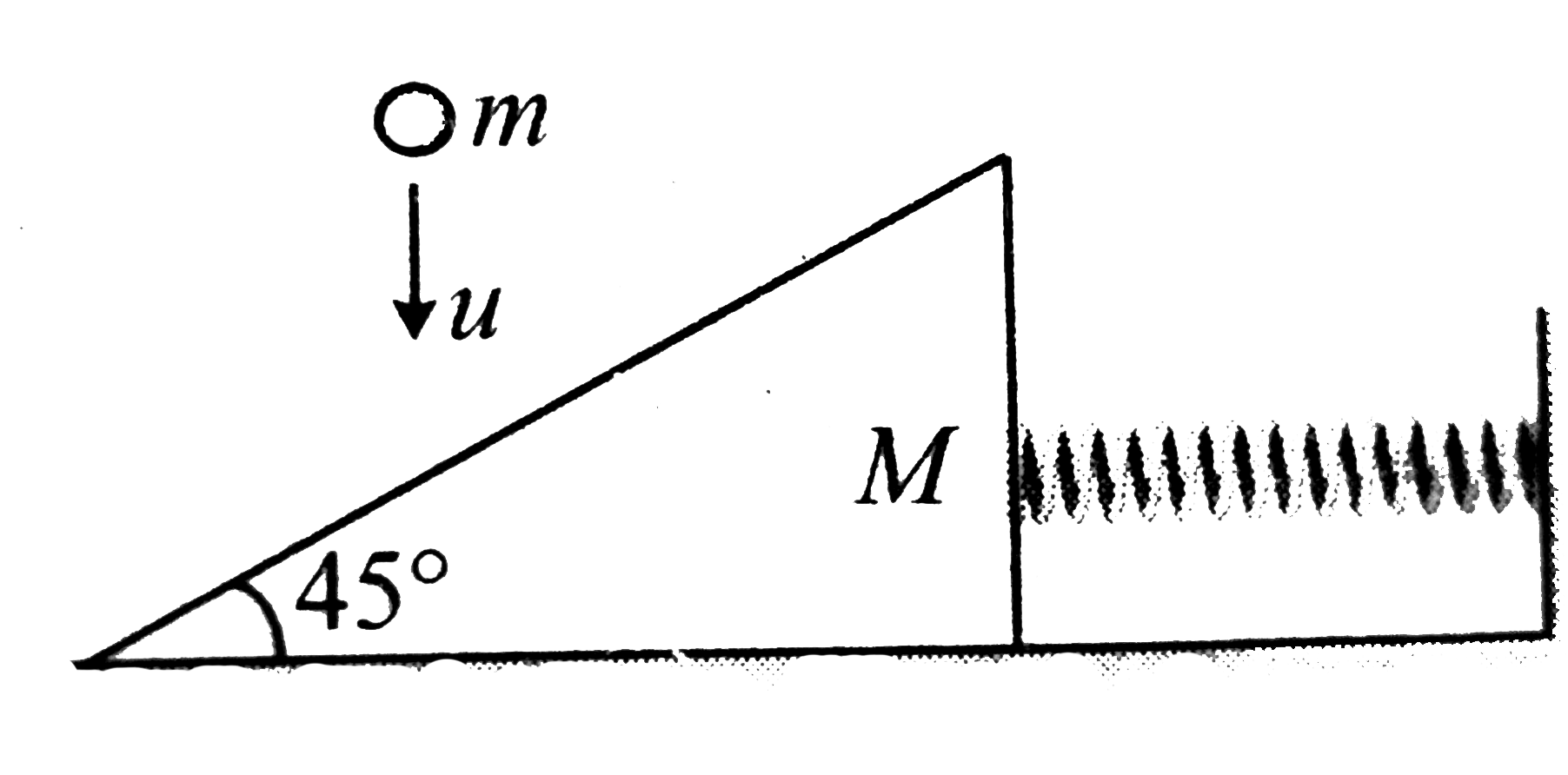 View Solution
View SolutionA ball of mass `m` moving with constant horizontal velocity `u` strikes a stationary wedge of mass `M` on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
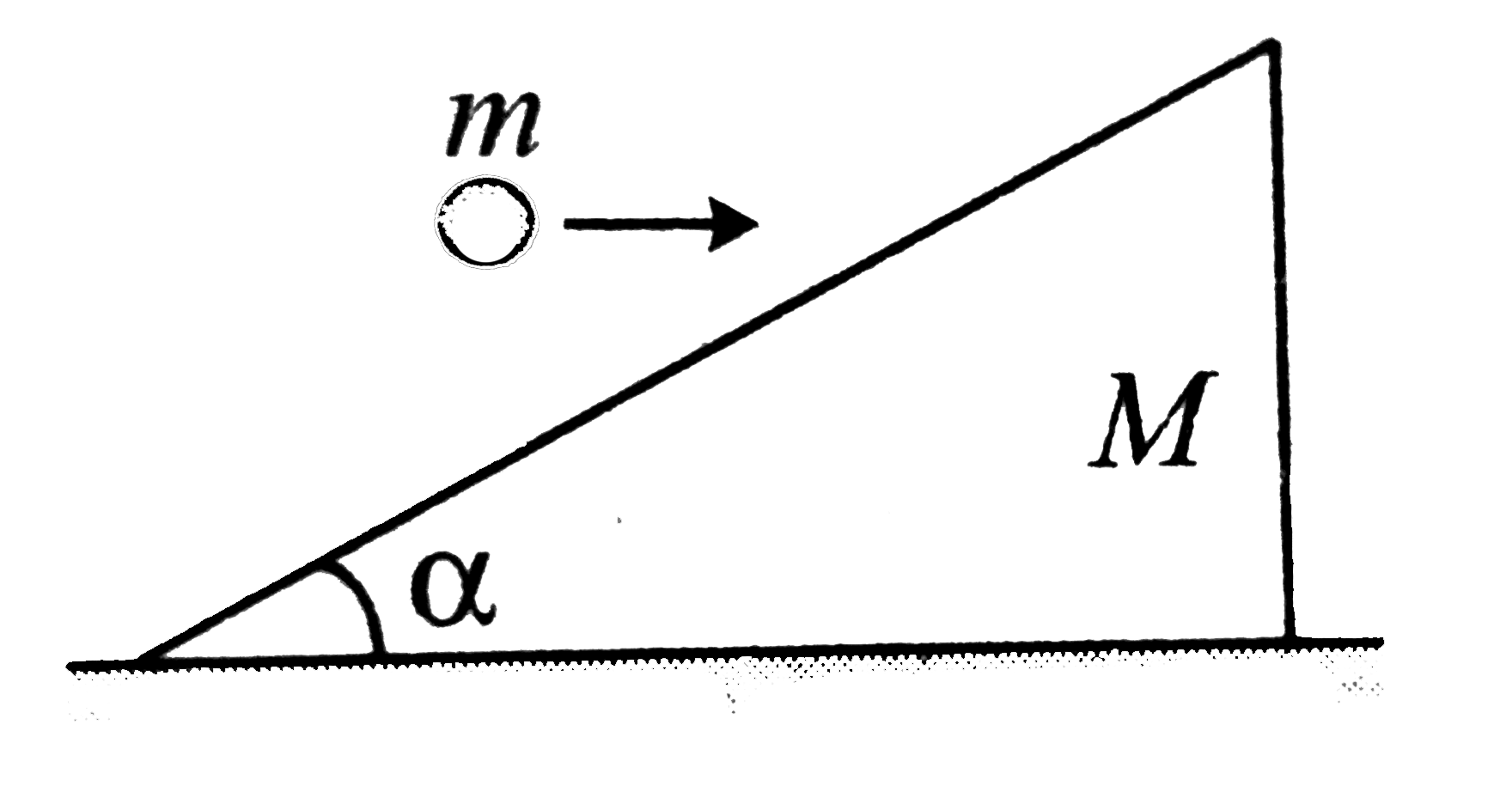 View Solution
View SolutionA ball of mass `m` collides with a stationary wedge of mass `M`, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is `e`, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.
 View Solution
View SolutionA small bucket of mass `M` is attached to a long inextensible cord of length `L`. The bucket is released from rest when the cord is in a horizontal position. In its lowest position the bucket scoops up m of water, what is the height of the swing above the lowest position?
08:31View SolutionTwo wooden plank of mass `M_(1)= 1 kg, M_(2) = 2.98 kg` smooth surface. A bullet of mass `m = 20 gm` strikes the block `M_(1)` and pierces through it, then strikes the plank `B` and sticks to its. Consequently both the planks move with equal velocities. Find the percentage change in speed of the bullet when it escapes from the first block.
03:29View SolutionIn the diagram shown, no friction at any contact surface. Initially, the spring has no deformation. What will be the maximum deformation in the spring ? Consider all the strings to be sufficiency large. Consider the spring constant to be `K`.
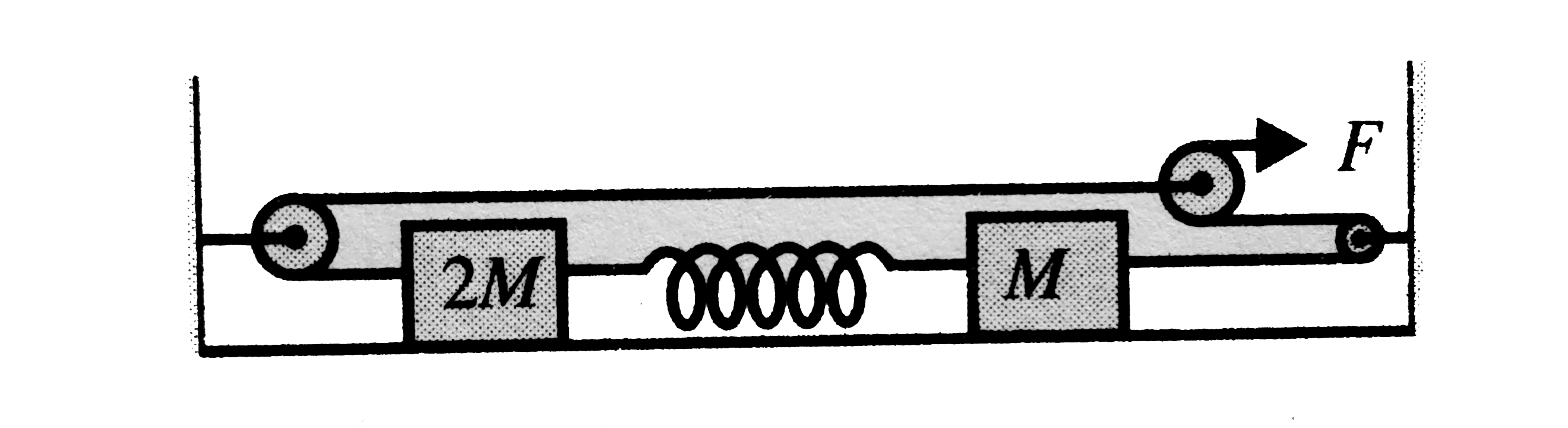 View Solution
View SolutionTwo blocks `A` and `B` of mass `m` and `2m` respectively are moving towards a massive (`"mass" gt gt 2m`) cliff with velocities `2v` and `v` respectively. The cliff moves with a velocity `v`. If the coefficient of restitution of collision at the surface of the cliff is `e = 1//2`, find the:

a. velocity of the block `B` just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness `k` which is fitted with the block `B`.View SolutionA boy throws a ball with initial speed `sqrt(ag)` at an angle `theta` to the horizontal. It strikes a smooth vertical wall and returns to his hand. Show that if the boy is standing at a distance 'a' from the wall, the coefficient of restitution between the ball and the wall equals `1/((4sin2theta-1))`. Also show that `theta` cannot be less than `15^(@)`.
View SolutionA ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View SolutionA ball is projected form a point `A` on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle `theta` with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find `e` in terms of `alpha` and `theta`. Here `e` is the coefficient of restitution between the ball and the plane.
View SolutionA small ball of mass `m` is connected by an inextensible massless string of length with an another ball of mass `M = 4m`. They are released with zero tension in the string from a height `h` as shown in the figure. Find the time when the string becomes taut for the first time after the mass `M` collides with the ground. Take all collisions to be elastic.
 04:14View Solution
04:14View SolutionTwo balls `A` and `B` each of mass `m` are placed on a smooth ground as shown in the figure. Another ball `C` of mass `M` arranged to the right of ball `B` as shown. If a velocity `v_(1)` is given to ball `A` in rightward direction, consider two cases. Case-I `M gt m` and case-II `M lt m`. Take all the collisions perfectly elastic (`e = 1`), find the number of collision in case-I and case-II.
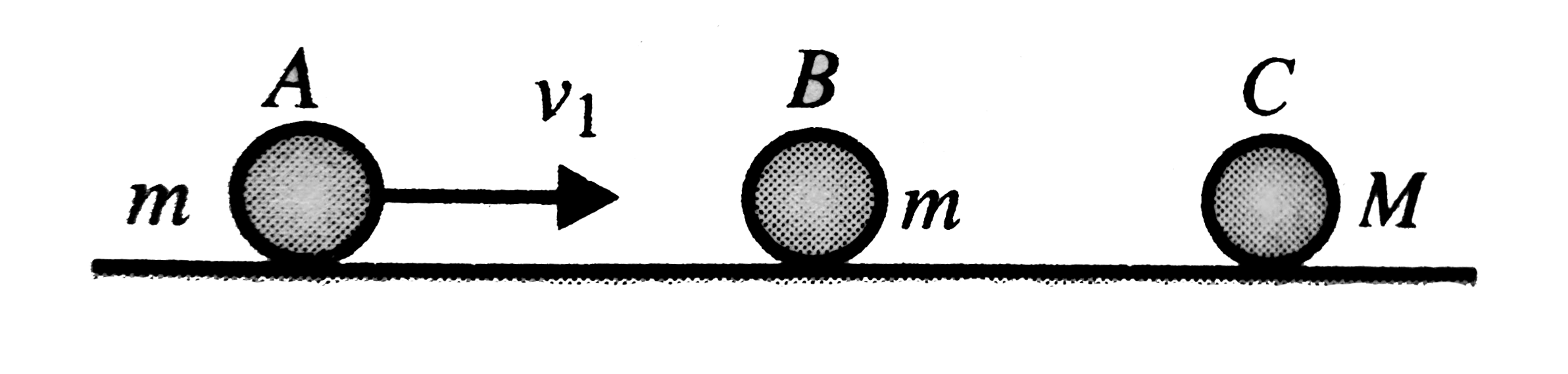 View Solution
View Solution
Subjective questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11
