Complete Solutions to Single Correct of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An object initially at rest explodes into three fragments `A, B` and `C`. The momentum of `A` is `phati` and that of `B` is `sqrt(3)phatj`
where `p` is `a +ve` number. The momentum of `C` will be02:24View SolutionA ball collides impinges directly on a similar ball at rest. The first ball is brought to rest after the impact. If half of the kinetic energy is lost by impact, the value of coefficient of restitution `( e)` is
01:34View SolutionA `20 g` bullet pierces through a plate of mass `M_(1) = 1 kg` and then comes to rest inside a second plate of mass `M_(2) = 2.98 kg` as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between `M_(1)` and `M_(2`. Neglect any loss of material of the plates due to the action of bullet.
 08:08View Solution
08:08View SolutionA particle of mass `m` is moving horizontally with a constant velocity `v` towards a rigid wall that is moving in opposite direction with a constant speed `u`. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
02:10View SolutionTwo identical balls `A` and `B` are released from the position shown in Fig. They collide elastically with each other on the horizontal portion. The ratio of heights attained by `A` and `B` after collision is (neglect friction)
 07:25View Solution
07:25View SolutionBlock `A` of mass` M = 2 kg` is connected to another block `B` of mass `m= 1 kg` with a string and a spring of force constant `k = 600 N//m` as shown in Fig. Initially, spring is compressed to `10 cm` and whole system is moving on a smooth surface with a velocity `v = 1 m//s`. At any time, thread is burnt, the velocity of block `A`, when `B` is having maximum velocity w.r.t. ground, is
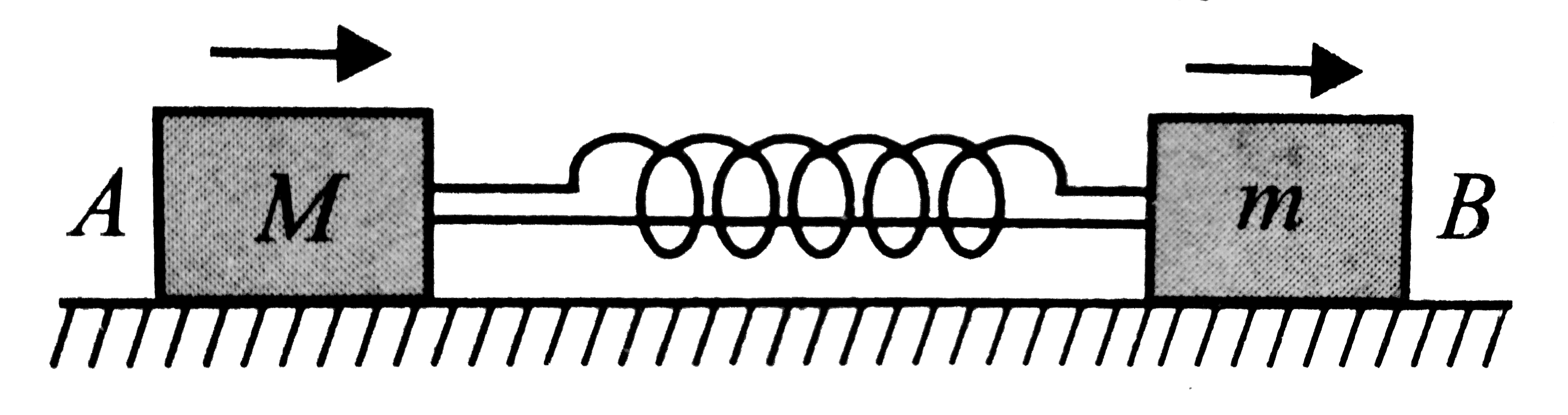 View Solution
View SolutionTwo identical blocks, each having mass M, are placed as shown in figure. These two blocks A and B are smoothly conjugated, so that when another block C of mass m passes from A to B there is no jerk. All the surfaces are frictionless, and all three blocks are free to move. Block C is released from rest, then
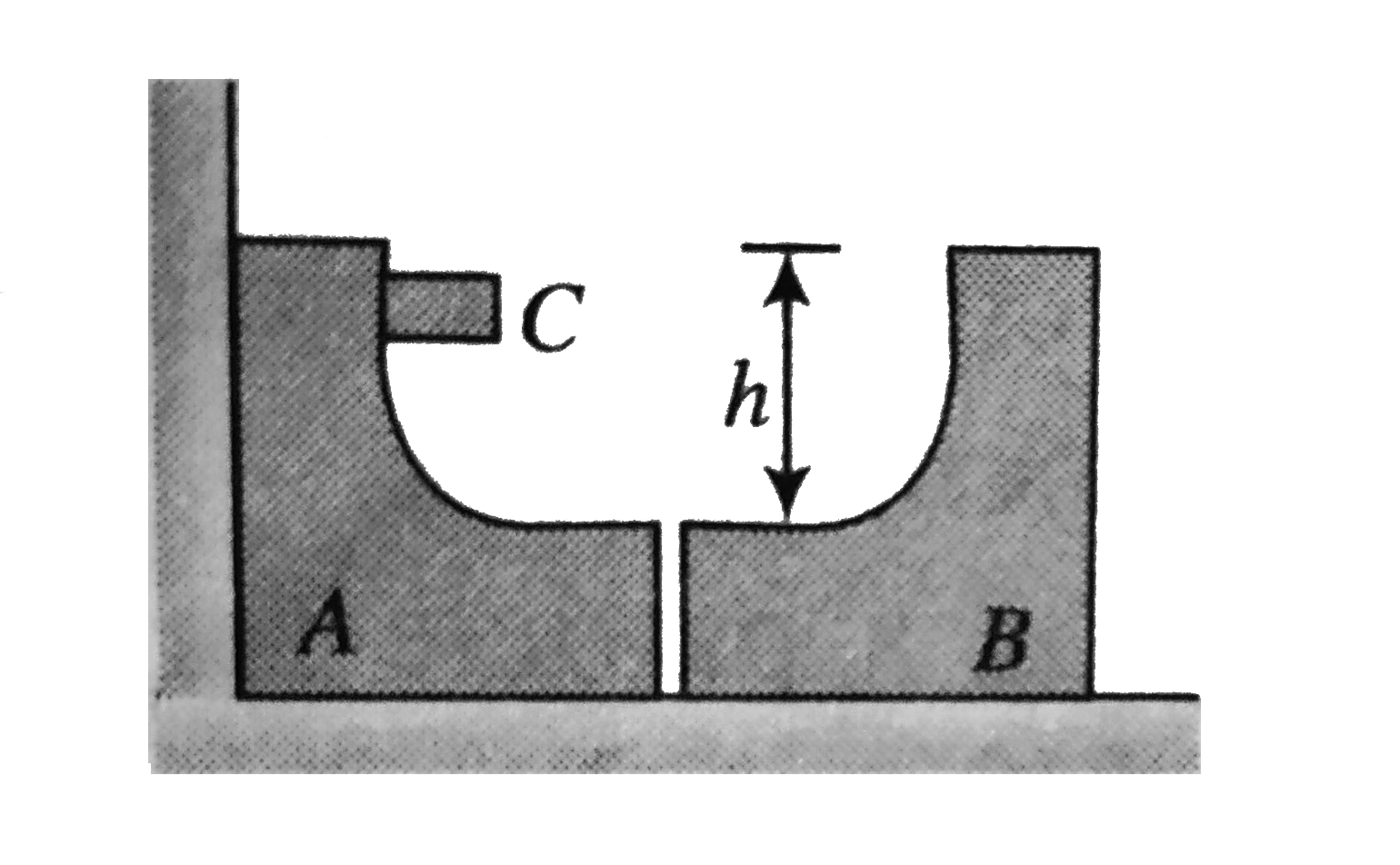 04:11View Solution
04:11View SolutionA bob of mass `10m` is suspended through an inextensible string of length `l`. When the bob is at rest in equilibrium position, two particles, each of mass `m`, strike it as shown in Fig. The particles stick after collision. Choose the correct statement from the following:
 05:47View Solution
05:47View SolutionIn Fig., a hollow tube of mass `M` is free in horizontal direction. The system is released from rest. There is no friction present. The tube and blocks are taken as system.
i. Momentum of the system is conserved in x-direction.
ii. Speed of `A` w.r.t. `M =` speed of `B` w.r.t. `M`.
iii. Trajectory of centre of mass is `X`-constant. iv. Centre of mass has finite acceleration.
Evaluate the above statements and choose the correct option from the following:
 02:46View Solution
02:46View SolutionA particle of mass `m` travelling with velocity `v` and kinetic energy `E` collides elastically to another particle of mass `nm`, at rest. What is the fraction of total energy retained by the particle of mass `m`?
04:05View SolutionA ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
03:14View SolutionA trolley was moving horizontally on a smooth ground with velocity `v` with respect to the earth. Suddenly a man starts running from rear end of the trolley with a velocity `(3//2)v` with respect to the trolley. After reaching the other end, the man turns back and continues running with a velocity `(3//2)v` with respect to trolley in opposite direction. If the length of the trolley is L, find the displacement of the man with respect to earth when he reaches the starting point on the trolley. Mass of the trolley is equal to the mass of the man.
04:03View SolutionIn a figure shown mass of `A` and `B` is equal to `M` each. Friction between `B` and lowermost surface is negligible. Initially both the blocks are at rest. The dimensions of the block `A` are very small. A constant horizontal force `F` is applied on the blocks `B` and both the blocks start moving together without any relative motion. Suddenly, the block `B` encounters a fixed obstacle and comes to rest. The block `A` continues to slide on the block `B`. The block `A` just manages to reach the opposite end of the bolck `B`. What is the coefficient of friction between the two blocks? (Required length are shown in figure)
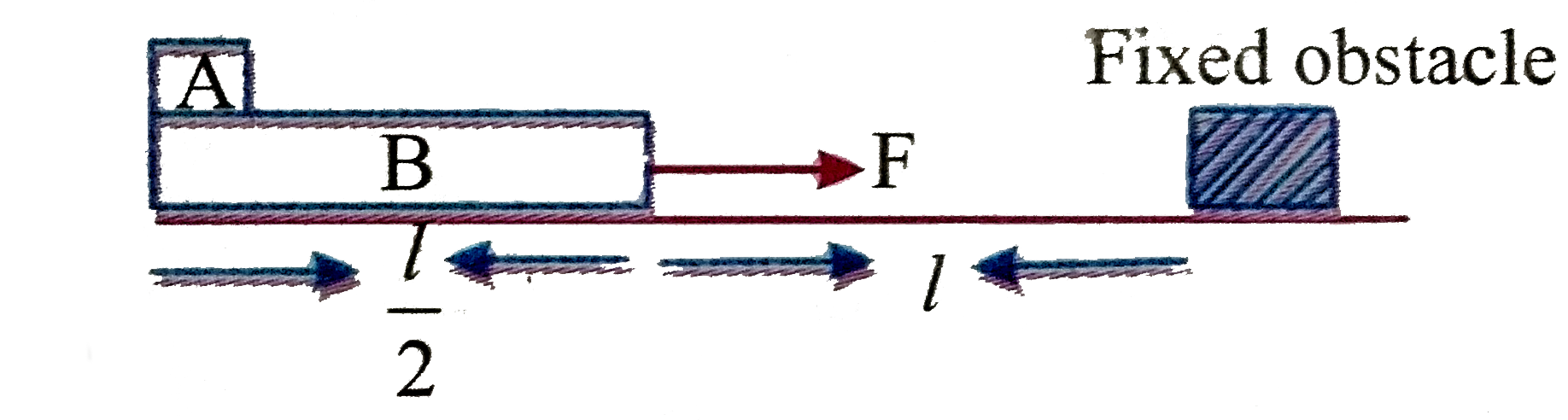 04:41View Solution
04:41View SolutionTwo blocks of masses in and `4m` lie on a smooth horizontal surface connected with a spring in its natural length. Mass `m` is given velocity `v_(0)` through an impulse as shown in Fig. Which of the following is not true about subsequent motion?
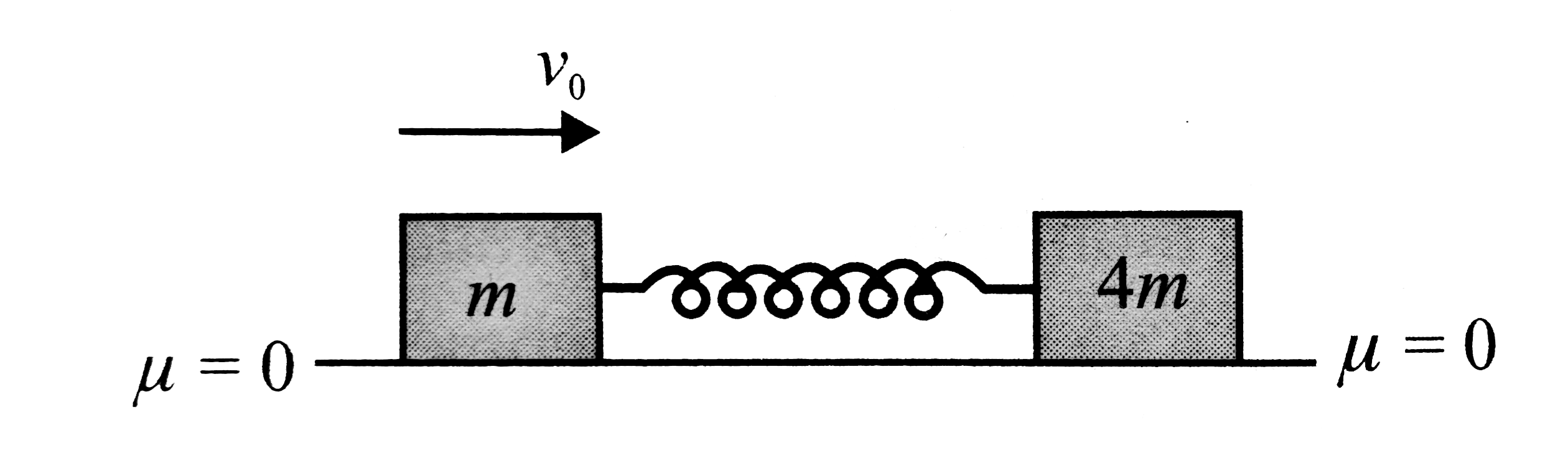 10:36View Solution
10:36View SolutionA vessel at rest explodes breaking it into three pieces. Two pieces having equal mass fly off perpendicular to one another with the same speed of `30 m//s`. The third piece has three times the mass of each of the other two pieces. What is the direction (w.r.t. the pieces having equal masses) and magnitude of its velocity immediately after the explosion?
View SolutionA stationary body of mass `3 kg` explodes into three equal pieces. Two of the pieces fly off at right angles to each other. One with a velocity of `2hati m//s` and the other withl velocity of `3hati m//s`. If the explosion takes place in `10^(-5)` the average force acting on the third piece in newtons
02:11View SolutionA ball of mass in collides horizontally with a stationary wedge on a rough horizontal surface, in the two orientations as shown. Neglect friction between the ball and the wedge. The students comment on the system of ball and wedge in these situations
 Saurav: Momentum of the system in `x`-direction will change by significant amount in both the cases. Rahul: There are no impulsive external forces in `x`-direction in both cases, hence the total momentum of the system in `x`-direction can be treated as conserved in both cases. View Solution
Saurav: Momentum of the system in `x`-direction will change by significant amount in both the cases. Rahul: There are no impulsive external forces in `x`-direction in both cases, hence the total momentum of the system in `x`-direction can be treated as conserved in both cases. View SolutionA body is hanging from a rigid support. by an inextensible string of length `'1'` . It is struck inelastically by an identical body of mass in with horizontal velocity `v=sqrt(2gl)` the tension in the string increases just after the striking by
02:05View SolutionA ball is let fall from a height `h_(0)`. There are `n` collisions with the earth. If the velocity of rebound after `n` collisions is `v_(n)` and the ball rises to a height `h_(n)` then coefficient of restitution `e` is given by
01:49View SolutionA body `X` with a momentum `p` collides with another identical stationary body `Y` one dimensionally. During the collision, `Y` gives an impulse `J` to body `X`. Then coefficient of restitution is
05:56View SolutionA pendulum consists of a wooden bob of mass in and of length `l`. A bullet of mass `m_(1)` is fired towards the pendulum with a speed `v_(1)`. The bullet emerges out of the bob with a speed `(v_(1))//3` and the bob just completes motion along a vertical circle. Then `v_(1)`is
01:38View SolutionTwo pendulums each of length `l` are initially situated as shown in Fig. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
 01:49View Solution
01:49View SolutionA wooden block of mass `10 g` is dropped from the top of a tower `100 m` high. Simultaneously, a bullet of mass `10 g` is fired from the foot of the tower vertically upwards with a velocity of `100 m//s`. If the bullet is embedded in it, how high will the block rise above the top of tower before it starts falling? `(g=10m//s^2)`
 02:36View Solution
02:36View SolutionA machinist starts with three identical square plates but cuts one corner from one of them, two corners from the second and three corners from the third. Rank the three according to the `x`-coordinate of their centre of mass, from smallest to largest.
 01:05View Solution
01:05View SolutionA particle of mass `2m` is projected at an angle of `45^@` with horizontal with a velocity of `20sqrt2m//s`. After `1s` explosion takes place and the particle is broken into two equal pieces. As a result of explosion one part comes to rest. Find the maximum height attained by the other part. Take `g=10m//s^2`.
06:53View SolutionA smooth sphere is moving on a horizontal surface with velocity vector `2hati+2hatj` immediately before it hits a vertical wall. The wall is parallel to `hatj` vector and the coefficient of restitution between the sphere and the wall is `e = 1//2`. The velocity vector of the sphere after it hits the wall is
View SolutionTwo equal spheres `A` and `B` lie on a smooth horizontal circular groove at opposite ends of a diameter. At time `t = 0`, A is projected along the groove and it first impinges on `B` at time `t = T_(1)` and again at time `t = T_(2)`. If `e` is the coefficient of restitution, the ratio `T_(2)//T_(1)` is
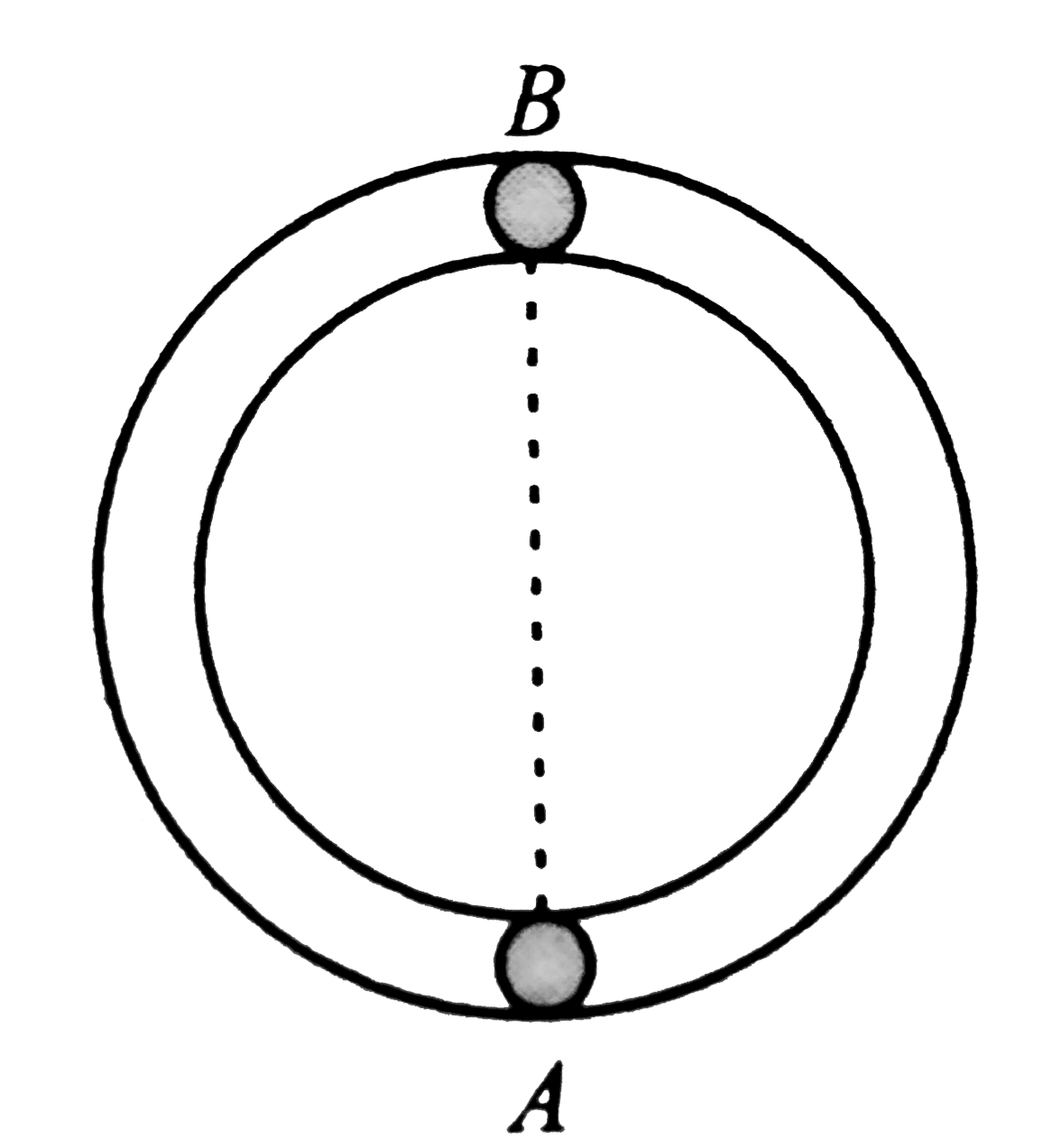 View Solution
View SolutionA block `'A'` of mass `m_1` hits horizontally the rear side of a spring (ideal) attached to a block `B` of mass `m_(2)` resting on a smooth horizontal surface. After hitting, `'A'` gets attached to the spring.
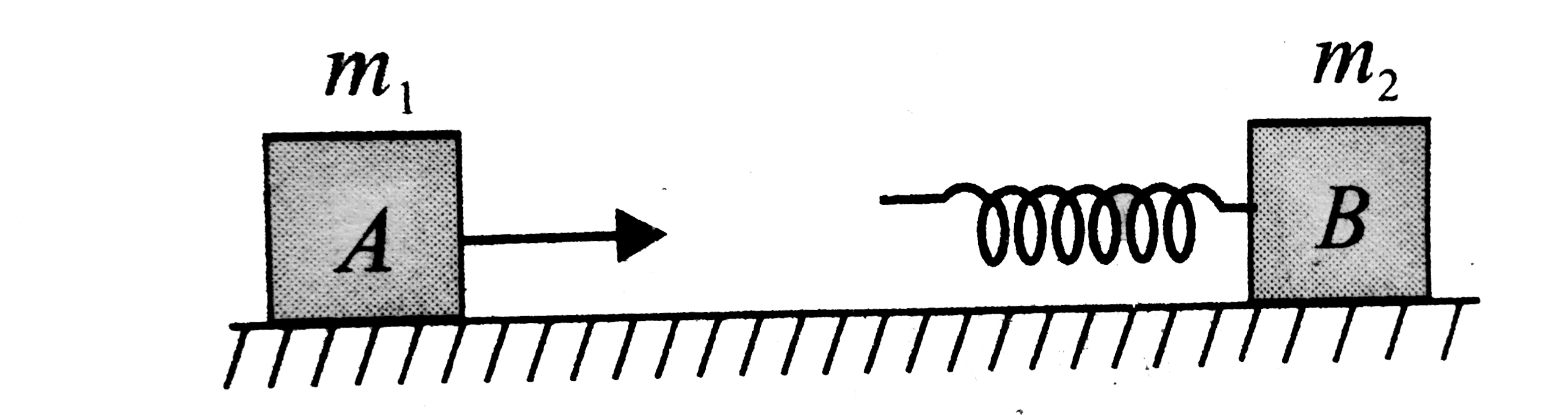
Some statements are given at any moment of time:
i. If velocity of `A` is greater than `B`, then kinetic energy of the system will be decreasing.
ii. If velocity of `A` is greater than `B`, then kinetic energy of the system will be increasing.
iii. If velocity of `A` is greater than `B`, then momentum of the system will be decreasing.
iv. If velocity of `A` is greater than `B`, then momentum of the system will be increasing.
Now select correct alternative:01:39View SolutionA particle of mass `4m` is projected from the ground at some angle with horizontal. Its horizontal range is `R`. At the highest point of its path it breaks into two pieces of masses `m` and `3m`, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance `x` from the point of projection, where `x` is equal to
03:13View SolutionA block of mass `M` is tied to one end of a massless rope. The other end of the rope is in the hands of a man of mass `2M` as shown in Fig. The block and the man art resting on a rough wedge of mass `M`. The whole system is resting on a smooth horizontal surface. The man starts walking towards right while holding the rope in his hands. Pulley is massless and frictionless. Find the displacement of the wedge when the block meets the pulley. Assume wedge is sufficiently long so that man does not fall down.
 View Solution
View SolutionA particle of mass `m_1` moving with velocity `v` in a positive direction collides elastically with a mass `m_(2)` moving in opposite direction also at velocity v. If `m_(2)gt gtm_(1)`, then
01:53View SolutionA strip of wood of mass `M` and length `l` is placed on a smooth horizontal surface. An insect of mass `m` starts at one end of the strip and walks to the other end in time `t`, moving with a constant speed. The speed of the insect as seen from the ground is
01:23View SolutionThe system in Fig. is released from rest from the position shown. After blocks have moved distance `H//3`. collar `B` is removed and block `A` and `C` continue to move. The speed of `C` just before it strikes the ground is
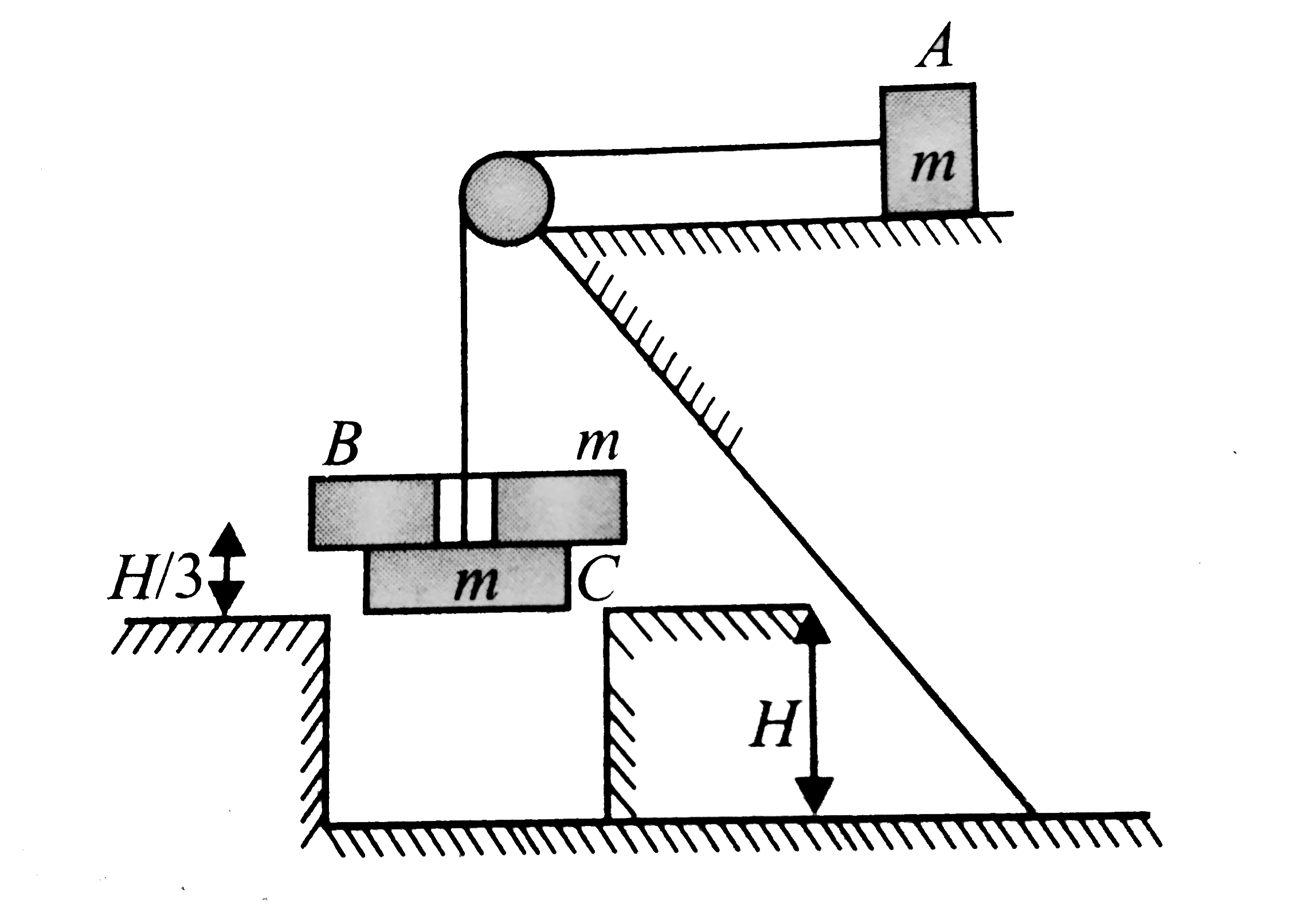 View Solution
View SolutionA car of mass `m` is initially at rest on the boat of mass `M` tied to the wall of dock through a massless, inextensible string. The car accelerates from rest to velocity `v_(0)` in times to. At `t = t_(0)` the car applies brake and comes to rest relative to the boat in negligible time. Neglect friction between the boat and water: the time `'t'` at which boat will strike the wall is
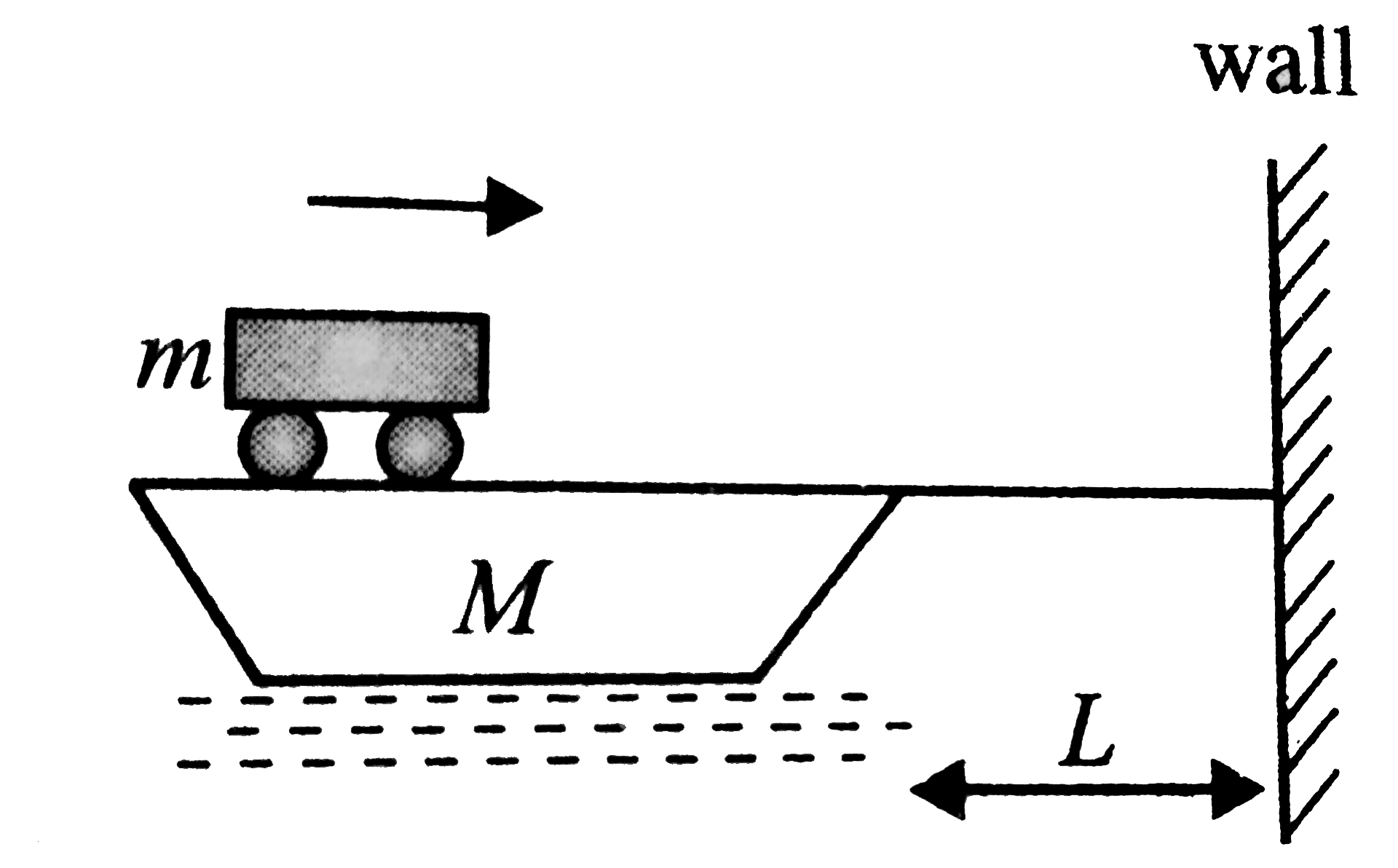 03:30View Solution
03:30View SolutionA partical of mass `m` moving with velocity `1m//s` collides perfectly elastically with another particle of mass `2m`. If the incident particle is deflected by `90^(circ)`. The heavy mass will make and angle `theta` with the initial direction of `m` equal to:
05:03View SolutionA canon shell moving along a straight line bursts into two parts. Just after the burst one part moves with momentum `20 N s` making an angle `30^(@)` with the original line of motion. The minimum momentum of the other part of shell just after the burst is
02:54View SolutionFigure shows a hollow cube of side `'a'` and volume `'V'`. There is a small chamber of volume `V//4` in the cube as shown. The chamber is completely filled by in kg of water. Water leaks through a hole `H` and spreads in the whole cube. Then the work done by gravity in this process assuming that the complete water finally lies at the bottom of the cube is
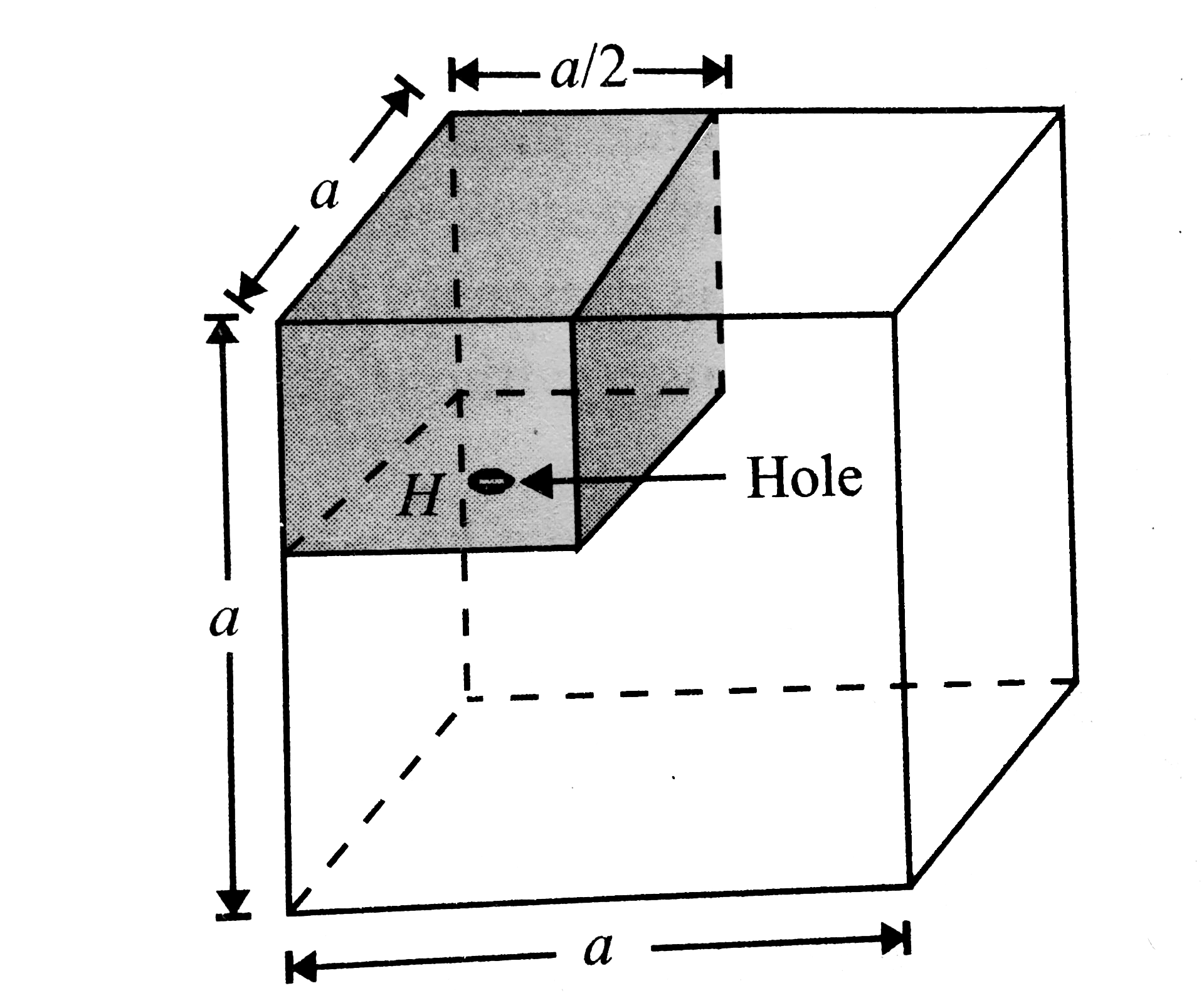 06:24View Solution
06:24View SolutionTwo men `'A'` and `'B'` are standing on a plank. `'B'` is at the middle of the plank and `'A'` is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. `'A'` and `'B'` start moving such that the position of `'B'` remains fixed with respect to ground, then `'A'` meets `'B'`. Then the point where `A` meets `B` is located at
 02:06View Solution
02:06View SolutionA gun which fires small balls of mass `20 g` is firing `20 balls` per second on the smooth horizontal table surface `ABCD`. If the collision is perfectly elastic and balls are striking at the centre of table with a speed of `5 m//s` at an angle of `60^(@)` with the vertical just before collision, then force exerted by one of the legs on ground is (assume total weight of the table is `0.2 kg`)
 07:18View Solution
07:18View SolutionFigure shows the velocity-time graph for two masses `R` and `S` that collided elastically. Which of the following statements is true?

i. `R` and `S` moved in the same direction after the collision.
ii. The velocities of `R` and `S` were equal at the mid time of the collision.
iii. The mass of `R` was greater than mass of `S`.
Which of the following is true?01:45View SolutionA system of two blocks `A` and `B` are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass `m` moving with a velocity `u` as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass `3m` is
 02:49View Solution
02:49View SolutionA stationary body explodes in to four identical fragments such that three of them fly mutually perpendicular to each other, each with same `KE(E_(0))`. The energy of explosion will be
02:46View SolutionA man stands at one end of the open truck which can run on frictionless horizontal rails. Initially, the man and the truck are at rest. Man now walks to the other end and stops. Then which of the following is true?
02:17View SolutionFigure shows a thin uniform rod `50 cm` long and has a mass of `100 g`. A hollow metal ball is filled with air and has a diameter `10 cm` and total mass `50 g` is fixed to one end of the rod. At what point along its length will the ball and rod balance horizontally?
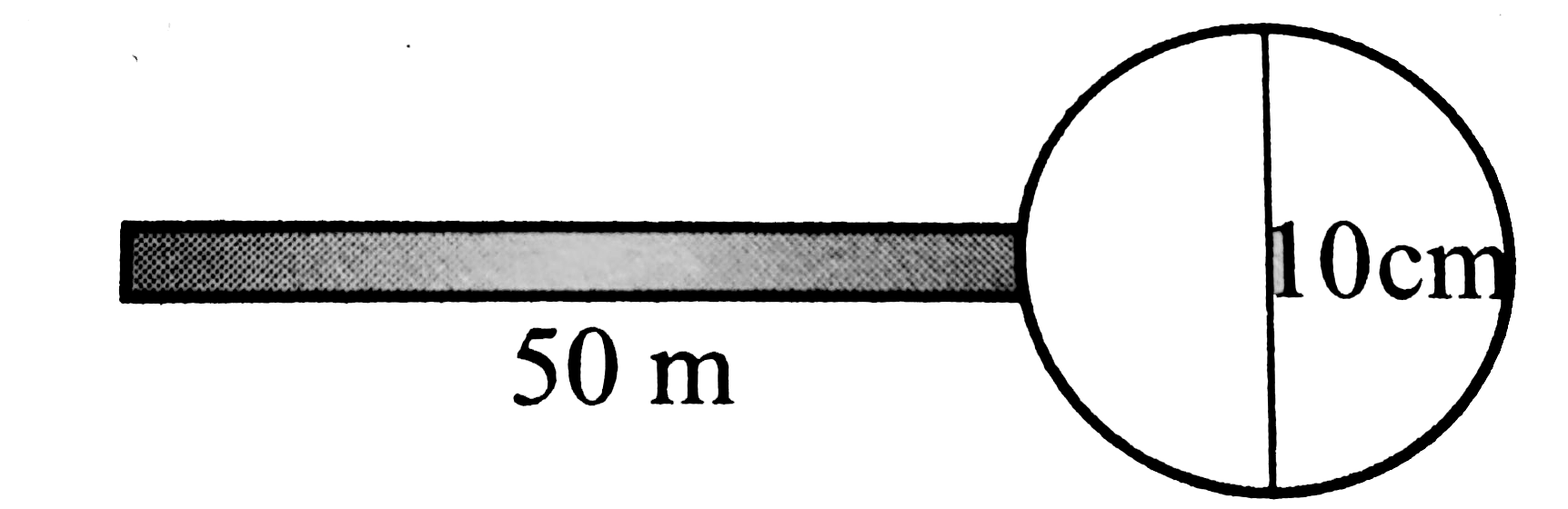 03:14View Solution
03:14View SolutionA hockey player receives a corner shot at a speed of `15 m//s` at angle `30^(@)` with `y`-axis and then shoots the ball along `x`-axis with the speed `30 m//s`. If the mass of the ball is `150 g` and it remains in contact with the hockey stick for `0.01 s`, the force exerted on the ball along `x`-axis is
 02:33View Solution
02:33View SolutionA ball is dropped from a height of `45 m` from the ground. The coefficient of restitution between the ball and the ground is `2/3`. What is the distance travelled by the ball in `4th` second of its motion. Assume negligible time is spent in rebounding. Let `g= 10 ms^(2)`
01:46View Solution`P` and `Q` are two identical masses at rest suspended by an inextensible string passing over a smooth frictionless pulley. Mass `P` is given a downward push with a speed `v` as shown in Fig. It collides elastically with the floor and rebounds immediately. What happens immediately after collision?
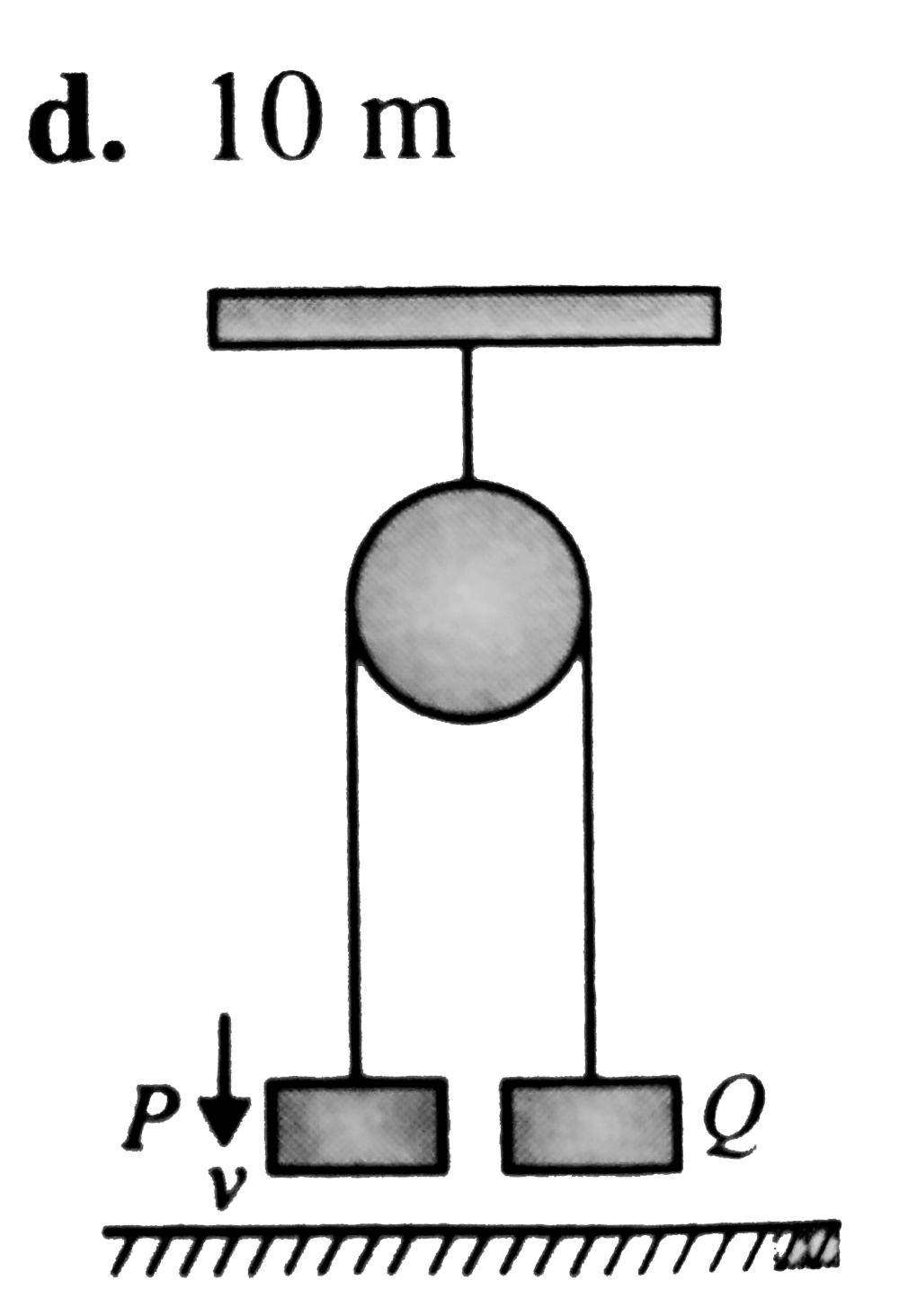 00:44View Solution
00:44View SolutionA bag of mass `M` hangs by a long massless rope. A bullet of mass in, moving horizontally with velocity `u`, is caught in the bag. Then for the combined (bag `+` bullet) system, just after collision
01:27View SolutionA man stands at one end of a boat which is stationary in water. Neglect water resistance. The man now moves to the other end of the boat and again becomes stationary. The centre of mass of the 'man plus boat' system will remain stationary with respect to water
01:36View SolutionTwo particles are shown in figure. At `t = 0` a constant force `F = 6 N` starts acting on `3 kg`. Find the velocity of circle of mass of these particle at `t = 5 s`.
 .02:04View Solution
.02:04View SolutionTwo blocks of masses `5 kg` and `2 kg` are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of `14 m//s` to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
06:35View SolutionIn a system of particles `8 kg` mass is subjected to a force of `16 N` along + ve `x`-axis and another `8 kg` mass is subjected to a force of `8 N` along + ve ` y`-axis. The magnitude of acceleration of centre of mass and the angle made by it with `x`-axis are given, respectively, by
01:09View SolutionA circular plate of uniform thickness has a diameter of `28 cm`. A circular portion of diameter `21 cm` is removed from the plate as shown. `O`is the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from `'O'` by
 02:47View Solution
02:47View SolutionA heavy chain of length `1 m` and weight `20 kg` hangs vertically with one end attached to a peg and carries a block of mass `10 kg` at the other end. Find the work done in winding `50 cm` of chain round the peg.
01:23View SolutionA cannon of mass `1000 kg` located at the base of an inclined plane fires a shell of mass `50 kg` in horizontal direction with velocity `180 km//h`. The angle of inclination of the inclined plane with the horizontal is `45^(@)`. The coefficient of friction between the cannon and inclined plane is `0.5`. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA `U`-shaped wire has a semicircular bending between `A` and `B` as shown in Fig. A bead of mass `m` moving with uniform speed `v` through a wire enters the semicircular bend at `A` and leaves at `B` with velocity `v//2` after time `T`. The average force exerted by the bead on the part `AB` of the wire is
 00:51View Solution
00:51View SolutionA particle of mass `2 kg` moving with a velocity of `3 m//s` is acted upon by a force which changes its direction of motion by an angle of `90^(@)` without changing its speed. What is the magnitude of impulse experienced by the particle?
00:45View SolutionA body of mass `3 kg` moving with a velocity of `4 m//s` towards left collides head on with a body of mass `4 kg` moving in opposite direction with a velocity of `3 m//s`. After collision the two bodies stick together and move with a common velocity which is
00:47View SolutionTwo blocks of masses `m_(1)= 2 kg` and `m_(2) = 4 kg` are moving in the same direction with speeds `v_(1) = 6 m//s` and `v_(2) = 3 m//s`, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant `k = 30000 N//m` is attached to the back side of `m_(2)`. Then the maximum compression of the spring after collision will be
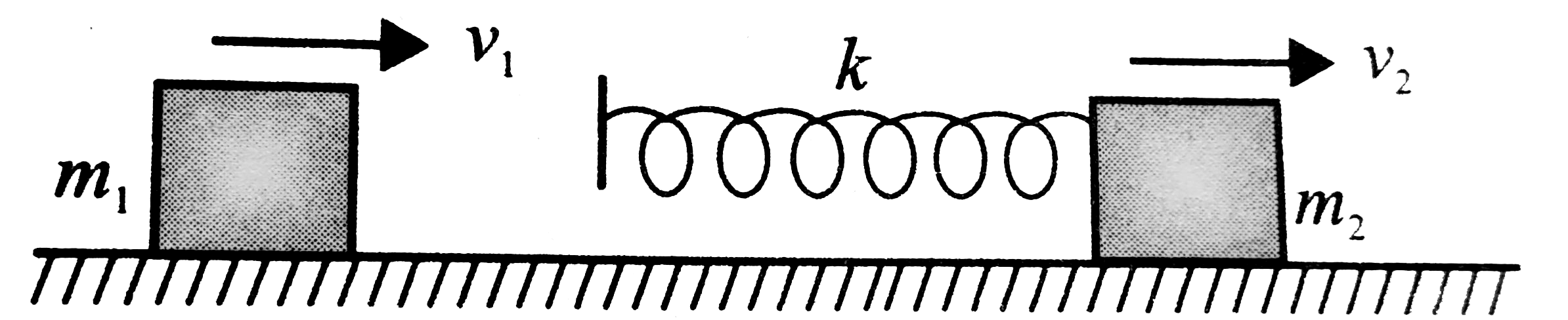 05:32View Solution
05:32View SolutionA cracker is thrown into air with a velocity of `10 m//s` at an angle of `45^(@)` with the vertical. When it is at a height of `0.5 m` from the ground, it explodes into a number of pieces which follow different parabolic paths. What is the velocity of centre of mass, when it is at a height of `1 m` from the ground? (`g = 10 m//s^(2)`)
04:35View SolutionA force exerts an impulse Ion a particle changing its speed from initial velocity `u` to final velocity `2u`. The applied force and the initial velocity are oppositely oriented along the same line. The work done by the force is
03:56View SolutionA ball falls vertically onto a floor with momentum `p` and then bounces repeatedly. If coefficient of restitution is `e`, then the total momentum imparted by the ball to the floor is
05:14View SolutionA ball released from a height ho above a horizontal surface rebounds to a height `h_(1)`, after one bounce. The graph that relates `h_(0)` to `h_(1)` is shown Fig. If the ball (of the mass `m`) was dropped from an initial height `h` and made three bounces, the kinetic energy of the ball immediately after the third impact with the surface was
 01:39View Solution
01:39View SolutionTwo identical balls, of equal masses `A` and `B`, are lying on a smooth surface as shown in Fig. Ball `A` hits ball `B` (which is at rest) with a velocity `v = 16 m//s`. What should be the minimum value of coefficient of restitution between `A` and `B` so that `B` just reaches the highest point of inclined plane?
 02:15View Solution
02:15View SolutionA particle of mass in is made to move with uniform speed `v_0` along the perimeter of a regular hexagon, inscribed in a circle of radius `R`. The magnitude of impulse applied at each corner of the hexagon is
01:31View SolutionA continuous stream of particles, of mass `m` and velocity `r`, is emitted from a source at a rate of `n` per second. The particles travel along a straight line, collide with a body of mass `M` and get embedded in the body. If the mass `M` was originally at rest, its velocity when it has received `N` particles will be
01:48View SolutionA ball kept in a close box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
02:22View SolutionA particle of mass `m` moving with a velocity `u` makes an elastic one-dimensional collision with a stationary particle of mass `m` establishing a contact with it for extremely small time. `T`. Their force of contact increases from zero to `F_0` linearly in time `T//4`, remains constant for a further time `T//2` and decreases linearly from `F_0` to zero in further time `T//4` as shown. The magnitude possessed by `F_0` is.
 .02:26View Solution
.02:26View SolutionA stationary body explodes into two fragments of masses `m_(1)` and `m_(2)`. If momentum of one fragment is `p`, the energy of explosion is
00:47View SolutionA ball of mass `m` is projected with a speed `v` into the barrel of a spring gun of mass `M` initially at rest lying on a frictionless surface. The mass sticks in the barrel at the point of maximum compression in the spring. The fraction of kinetic energy of the ball stored in the spring is
02:28View SolutionA railway flat car has an artillery gun installed on it. The combined system has a mass `M` and moves with a velocity `V`. The barrel of the gun makes an angle a with the horizontal. A shell of mass `m` leaves the barrel at a speed `v` relative to the barrel. The speed of the flat car so that it may stop after the firing is
05:20View SolutionTwo blocks of masses `6 kg` and `4 kg` are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
01:24View SolutionThe momentum of a moving particle is vectorially given a, `vecp=p_(0)(costhati+sinthatj)`where `t` stands for time. Choose the correct option:
02:00View SolutionA gun of mass `M`. fires a shell of mass `m` horizontally and the energy of explosion is such as would be sufficient to project the shell vertically to a height `'h'` . The recoil velocity of the gun is
02:47View SolutionAn inverted `T`-shaped object is placed on a horizontal floor as shown in Fig. A force `F` is applied on the system as shown in Fig. The value of `x` so that the system performs pure translational motion is
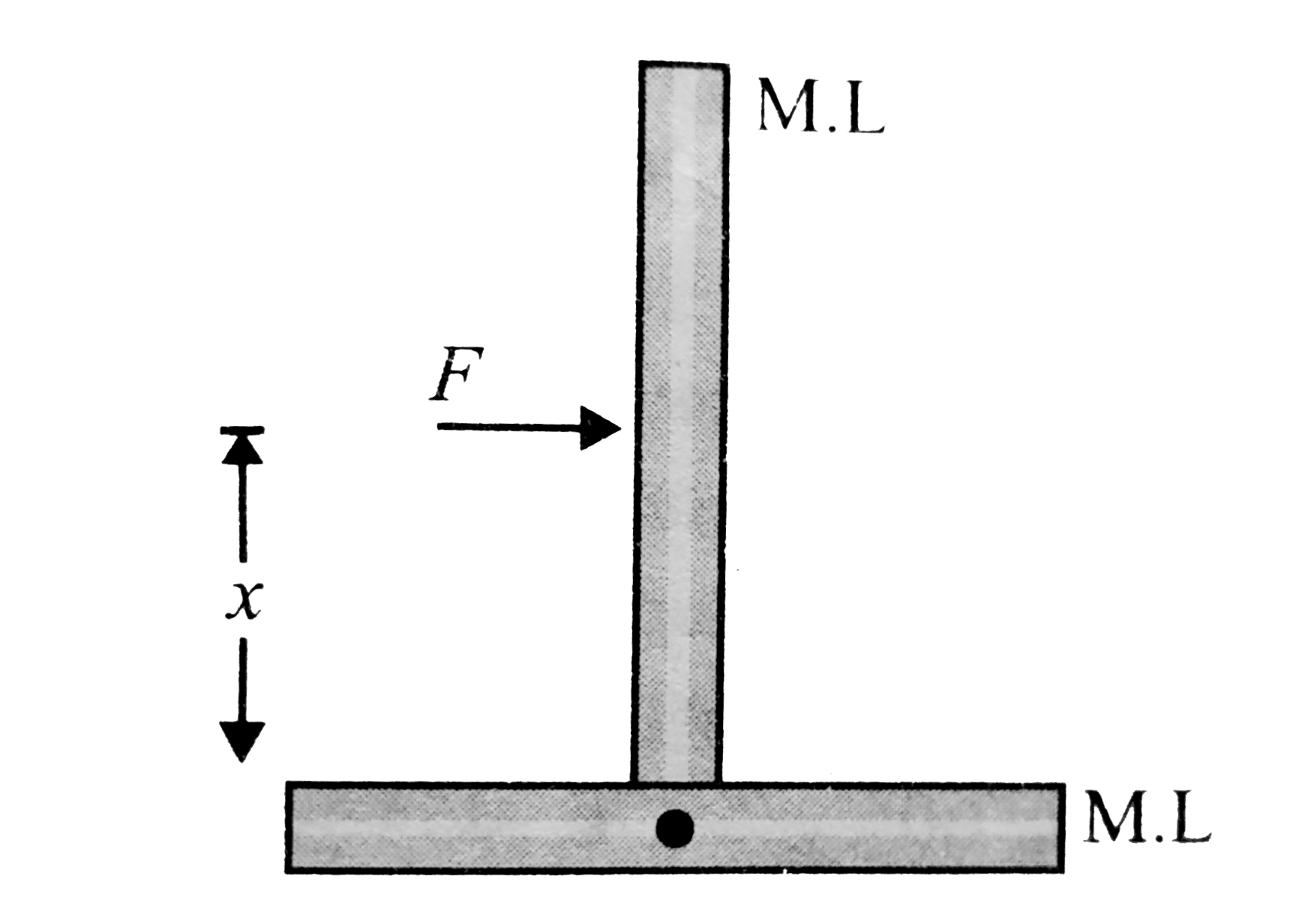 03:03View Solution
03:03View SolutionTwo blocks `m_(1)` and `m_(2)` are pulled on a smooth horizontal surface, and are joined together with a spring of stiffness `k` as shown in Fig. Suddenly, block `m_(2)` receives a horizontal velocity `v_(0)`, then the maximum extension `x_(m)` in the spring is
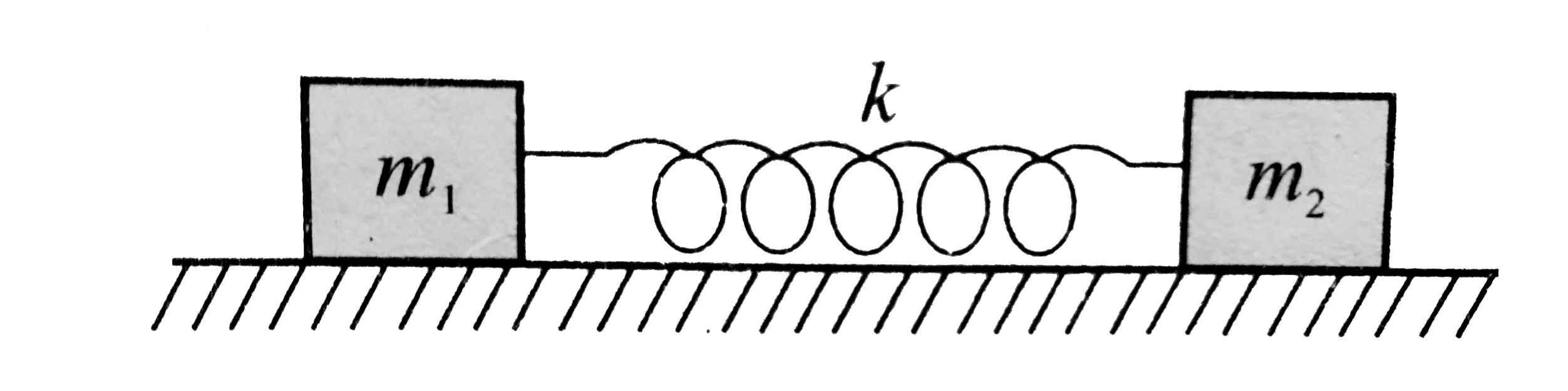 04:42View Solution
04:42View SolutionA particle at rest is constrained to move on a smooth horizontal surface. Another identical particle hits the fractional particle with a velocity `v` at an angle `theta=60^(@)` with horizontal. If the particles move together, the velocity of the combination just after impact is equal to
01:11View SolutionA particle of mass `m` comes down on a smooth inclined plane from point `B` at a height of `h` from rest. The magni-tude of change in momentum of the particle between position `A` (just before arriving on horizontal surface) and `C` (assuming the angle of inclination of the plane as `theta` with respect to the horizontal) is
 02:39View Solution
02:39View SolutionThree balls `A, B` and `C` of masses `2 kg, 4 kg` and `8 kg`, respectively, move along the same straight line and in the same direction, with velocities `4m//s,1m//s, 3/4m//s`. If `A` collides with `B` and subse-quently `B` collides with `C`, find the velocity of ball `A` and ball `B` after collision, taking the coefficient of restitution as unity.
 03:13View Solution
03:13View SolutionA ball of mass `m` moving with velocity `v_(0)` collides with a wall as shown in Fig. After impact it rebounds with a velocity' `(v_(0))//2`The component of impulse acting on the ball along the wall is
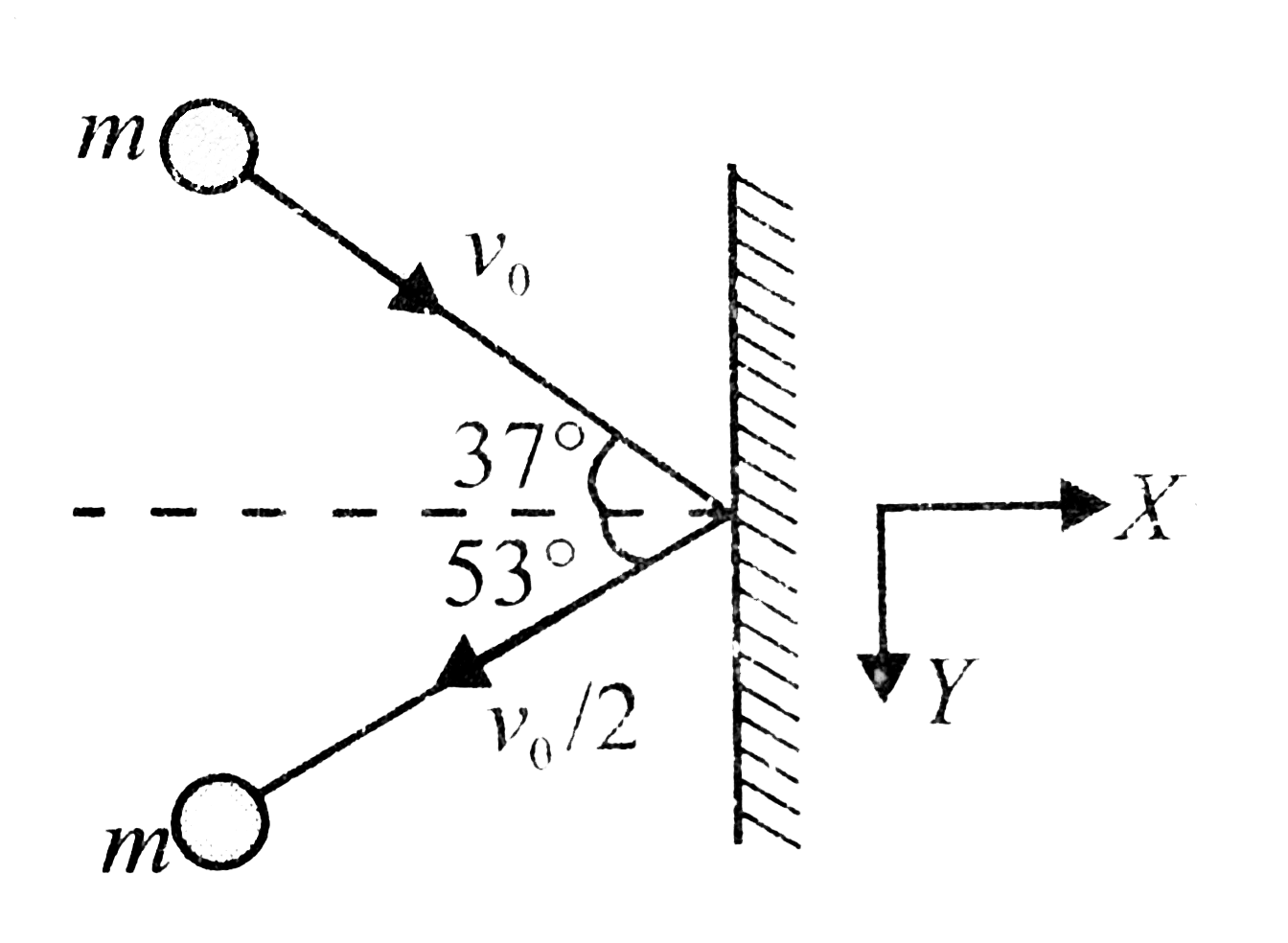 02:19View Solution
02:19View SolutionFive balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed `v_(0)` towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
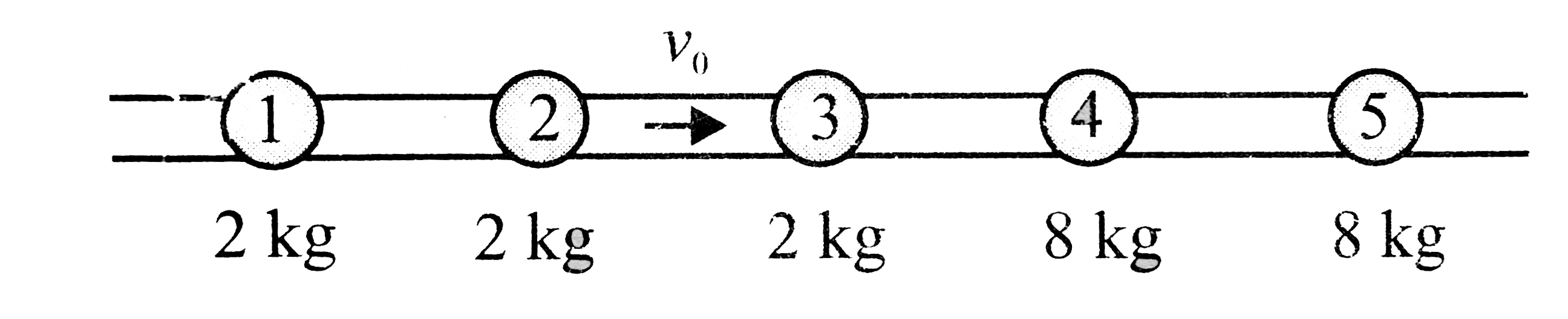 03:13View Solution
03:13View SolutionTwo objects are at rest on a level frictionless surface. The objects are not connected. A force `F` is applied to one of the objects, which then moves with acceleration a. Mark the correct statement(s).
01:28View SolutionA highly elastic ball moving at a speed of `3 m//s` approaches a wall moving towards it with a speed of `3 m//s`. After the collision. the speed of the ball will be
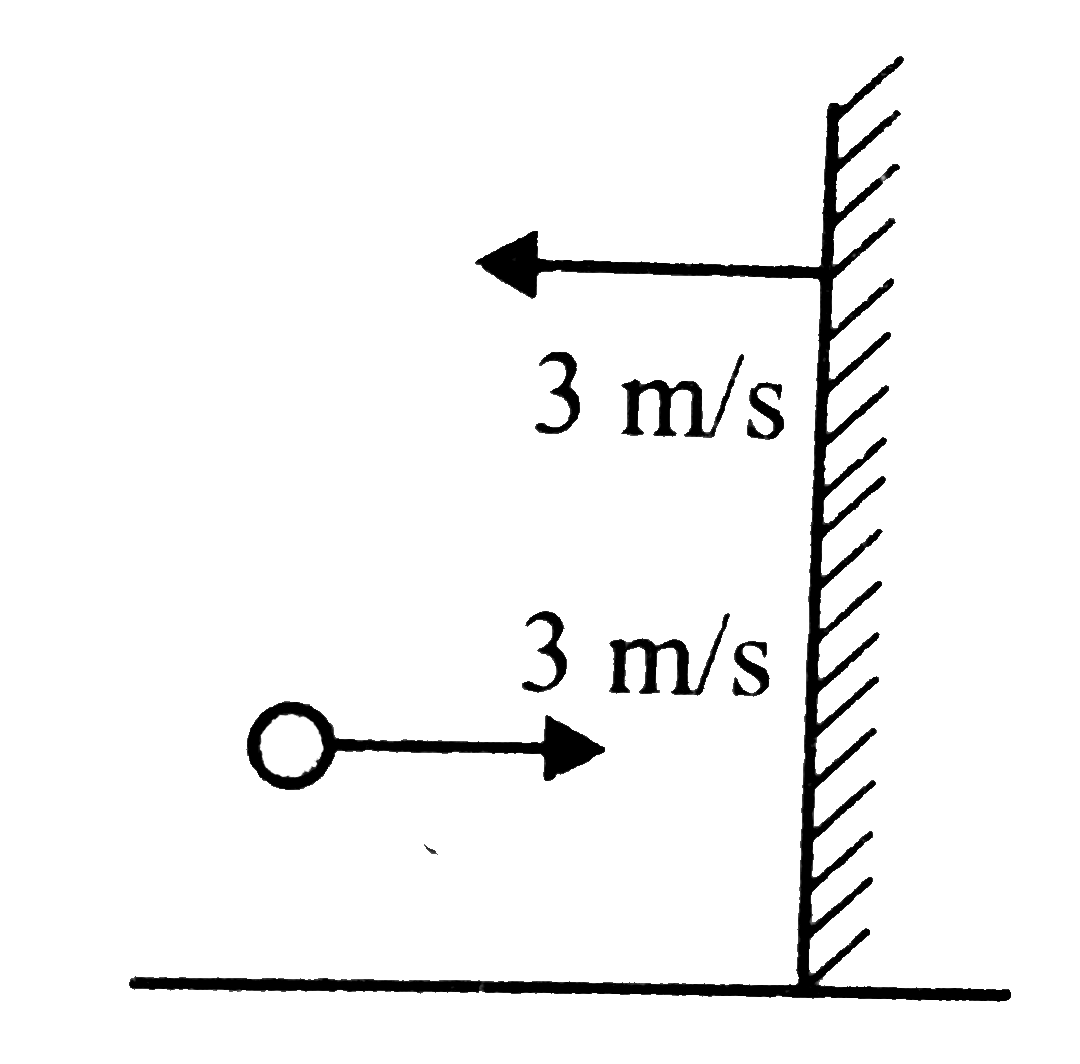 01:57View Solution
01:57View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of `37^(@)` with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionA ball of mass `m` is attached to a cord of length `L`, pivoted at point `O`, as shown in Fig. The ball is released from rest at point A, swings down and makes an inelastic collision with a block of mass `2m` kept on a rough horizontal floor. The coefficient of restitution of collision is `e = 2//3` and coefficient of friction between block and surface is After collision, the ball comes momentarily to rest at `C` when cord makes an angle of `theta` with the vertical and block moves a distance of `3L//2` on rough horizontal floor before stopping. The values of `mu` and `theta` are, respectively,
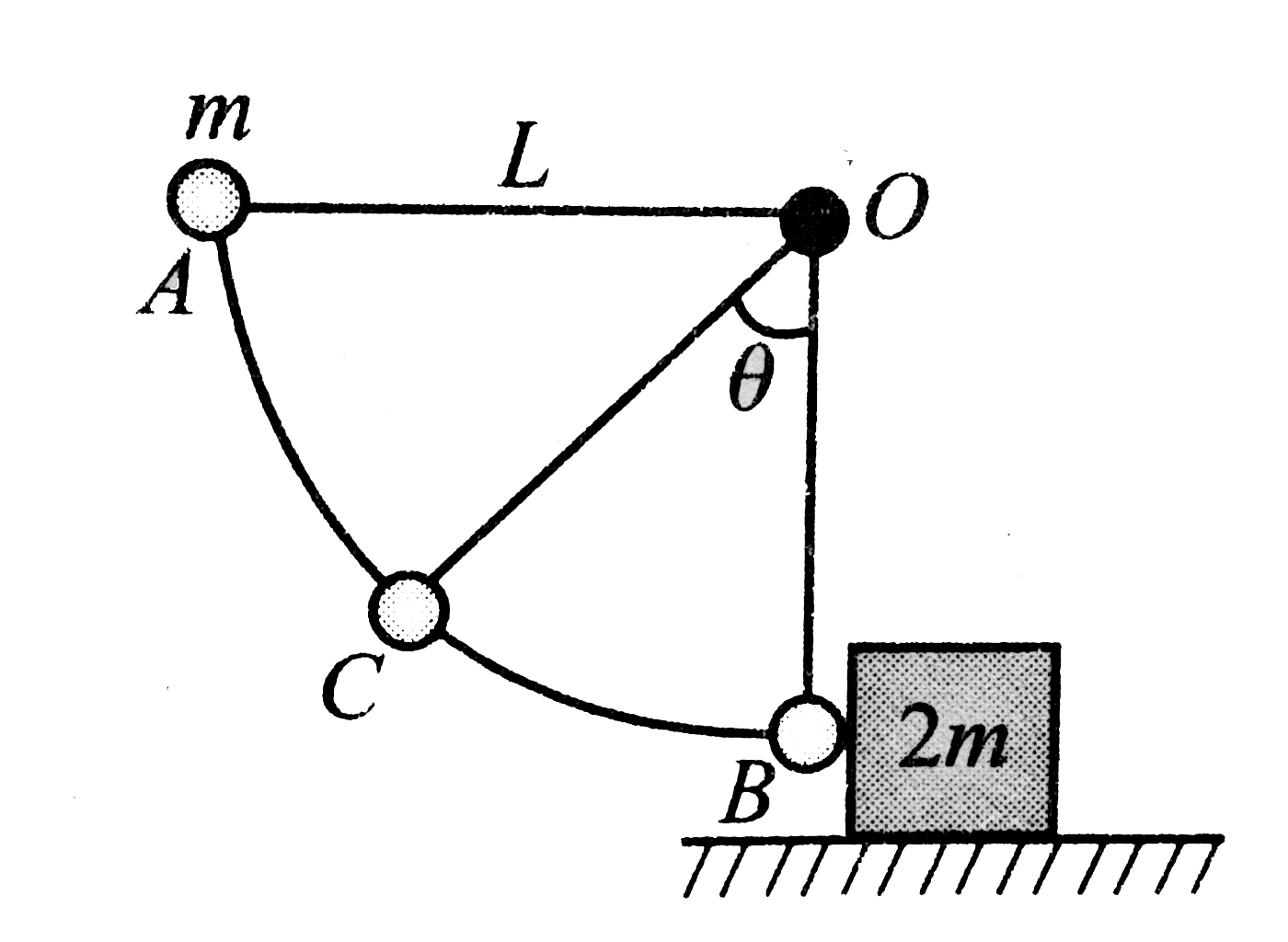 06:47View Solution
06:47View SolutionA ball of mass `m` is released from rest relative to elevator at a height `h`, above the floor of the elevator. After making collision with the floor of the elevator it rebounces to height `h_2`. The coefficient of restitution for Collision is `e`. For this situation, mark the correct statement(s).
 03:24View Solution
03:24View SolutionTwo blocks `A` and `B` of masses in and `2m`, respectively, are connected with the help of a spring having spring constant, `k` as shown in Fig. Initially, both the blocks arc moving with same velocity `v` on a smooth horizontal plane with the spring in its natural length. During their course of motion, block `B` makes an inelastic collision with block `C` of mass `m` which is initially at rest. The coefficient of restitution for the collision is `1//2`. The maximum compression in the spring is
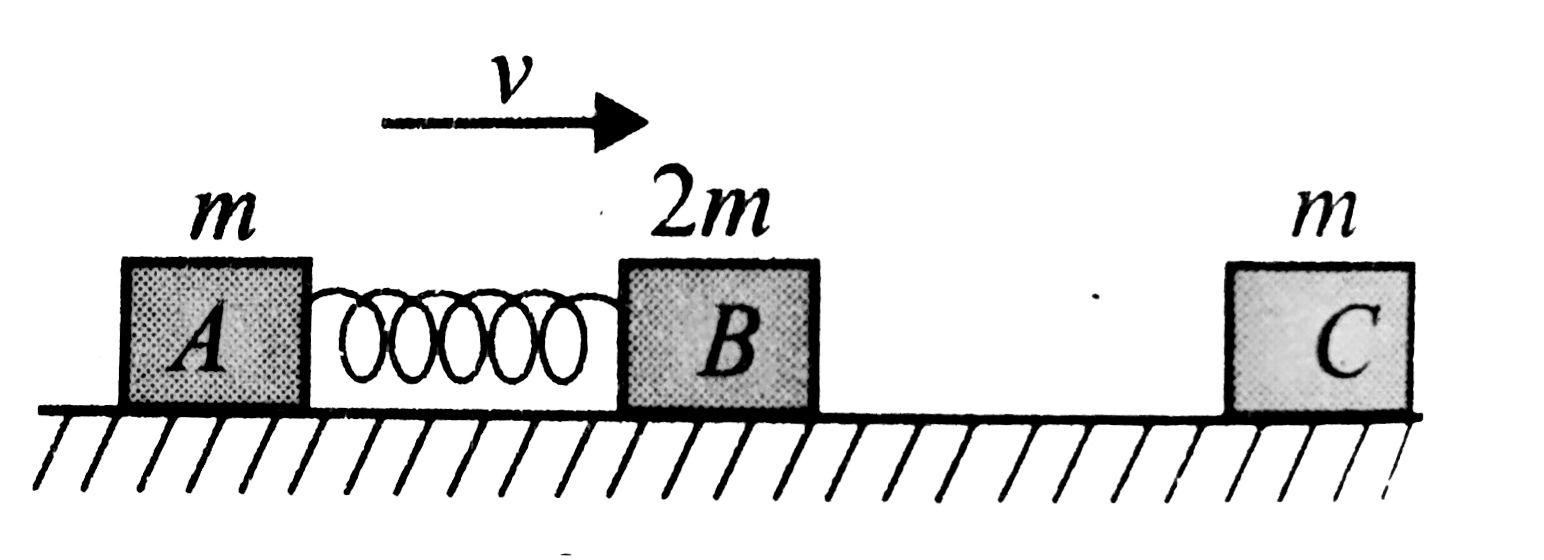 View Solution
View SolutionA `3000 kg` space probe is moving in a gravity free space at a constant velocity of `300 m//s`. To change the direction of space probe, rockets have been fired in a direction perpendicular to the direction of initial motion of the space probe, the rocket firing exerts a thrust of `4000 N` for `225 s`. The space probe will turn by an angle of (neglect the mass of the rockets fired)
02:18View SolutionAfter a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
02:55View SolutionAn object of mass `10 kg` is launched from the ground at `t = 0`, at an angle of `37^(@)` above the horizontal with a speed of `30 m//s`. At some time after its launch, an explosion splits the projectile into two pieces. One piece of mass `4 kg` is observed at (`105 m, 43 m`) at `t =2 s`. Find the location of second piece at `t = 2 s`?
 02:56View Solution
02:56View SolutionFor the system shown in Fig. the string is light and pulley is frictionless. The `4 kg` block is given an upward velocity of `1 m//s`. The centre of mass of the two blocks will [neglect the impulse duration]
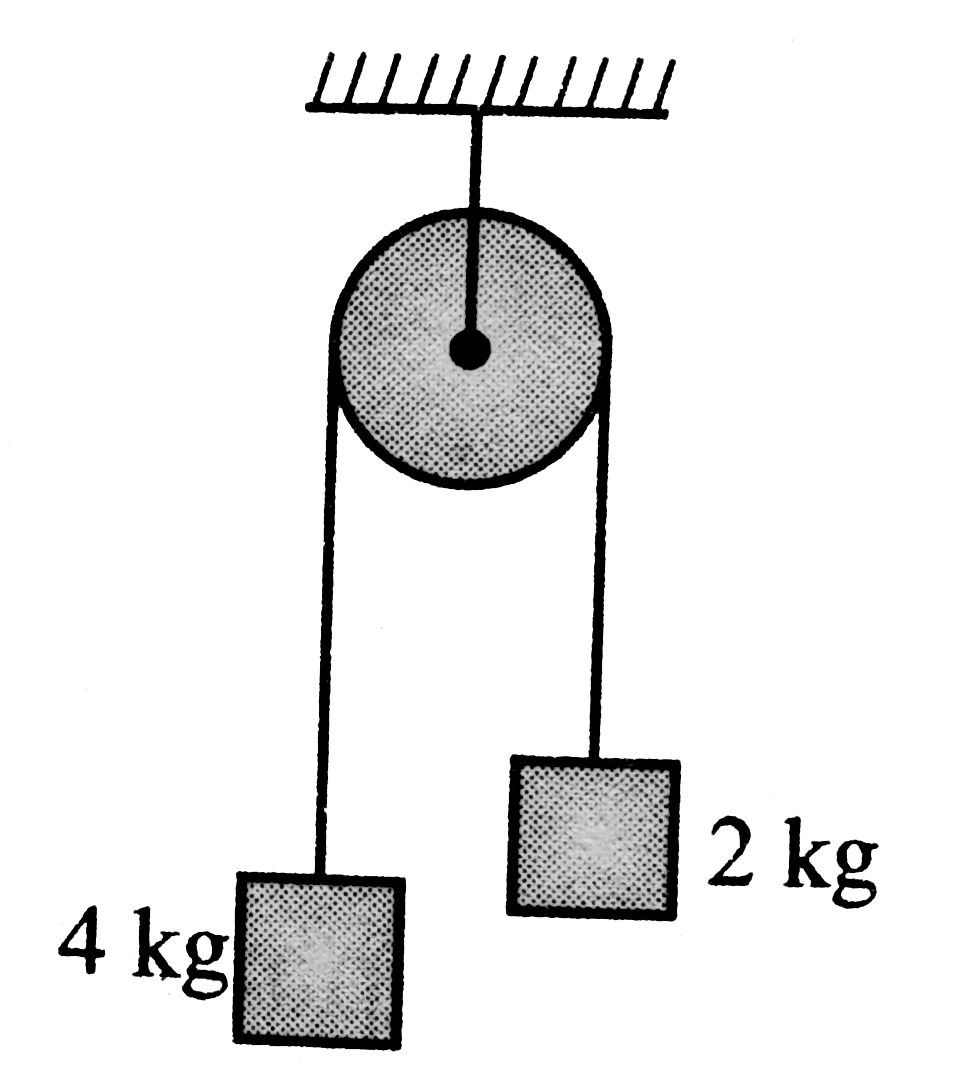 02:11View Solution
02:11View SolutionA parallel beam of particles of mass `m` moving with velocity `v` impinges on a wall at an angle `theta` to its normal. The number of particles per unit volume in the beam is `n`. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
05:03View SolutionA block of mass `m` starts from rest and slides down a frictionless semi-circular track from a height h as shown. When it reaches the lowest point of the track, it collides with a stationary piece of putty also having mass m. If the block and the putty . stick together and continue to slide, the maximum height that the block-putty system could reach is
 04:50View Solution
04:50View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is
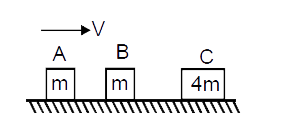 04:20View Solution
04:20View SolutionIn the figure shown, the two identical balls of mass `M` and radius `R` each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass `M` and radius `R//2`, is coming down vertically and has a velocity `= v_(0)` when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to
 View Solution
View SolutionThree blocks are placed on smooth horizontal surface and lie on same horizontal straight line. Block 1 and block 3 have mass `m` each and block 2 has mass `M (M gt gt m)`. Block 2 and block 3 are initially stationary, while block 1 is initially moving towards block 2 with speed `v` as shown. Assume that all collisions are head on and perfectly elastic. What value of `M//m` ensures that block 1 and block 3 have the same final speed?
 06:20View Solution
06:20View SolutionA particle of mass `m` is moving along the `x`-axis with speed v when It collides with a particle of mass `2m` initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? `(thetagt0)`
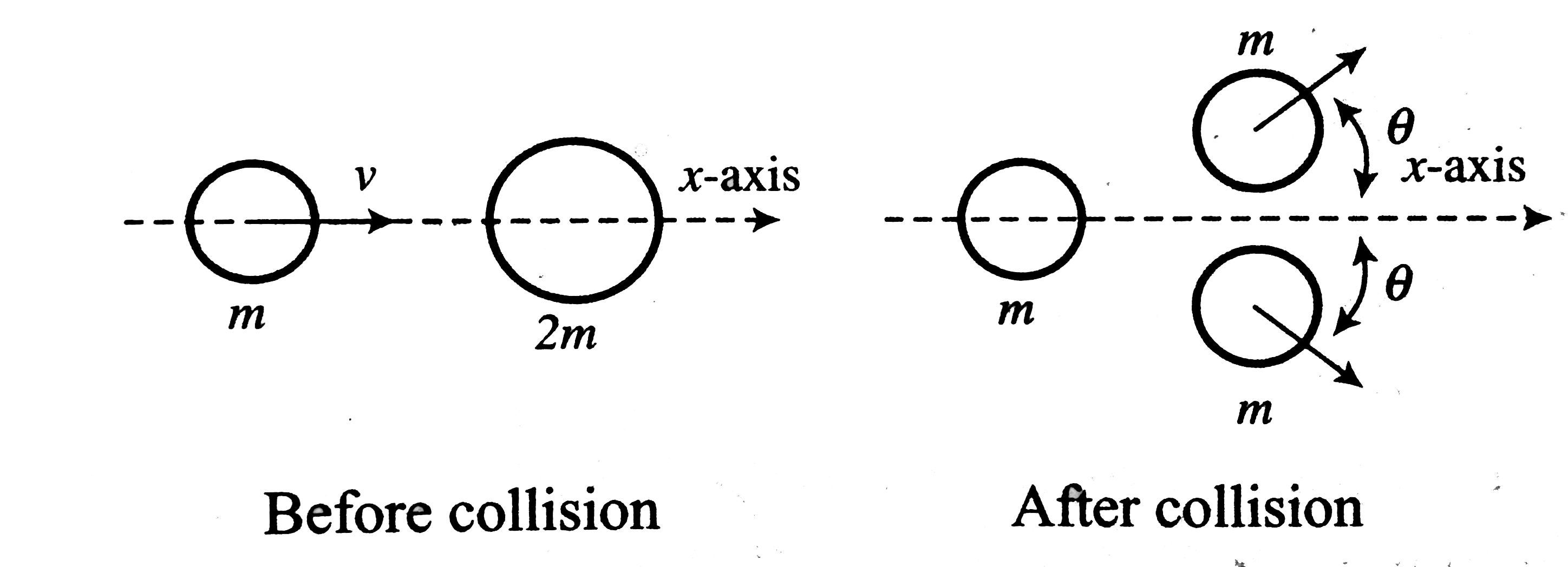 07:10View Solution
07:10View SolutionA particle of mass `m` is acted on by two forces of equal magnitude `F` maintaining their orientation relative to the velocity `v` as shown in Fig. The momentum of the particle
 00:50View Solution
00:50View SolutionThree particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle `A` starts with a velocity `v_(1)` towards line `AB`, particle `B` starts with a velocity `v_(2)` towards line `BC` and particle `C` starts with velocity `v_(3)` towards line `CA`. The displacement of `CM` of three particle `A, B` and `C` after time `t` will be (given if `v_(1)=v_(2)=v_(3))`
 04:44View Solution
04:44View SolutionA ball is projected in a direction inclined to the vertical and bounces on a smooth horizontal plane. The range of one rebound is `R`. If the coefficient of restitution is `e`, then range of the next rebound is
01:44View Solution
Single Correct questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11
