Complete Solutions to Exercise 1.3 of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Exercise 1.3 |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A ball is dropped on a floor from a height `h`. If the coefficient of restitution is `e`, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
01:35View SolutionAn elevator platform is going up at a speed of `20 m//s` and during its upward motion a small ball of `50 g` mass, falling in downward direction, strikes the platform at speed `5 m//s`. Find the speed with which the ball rebounds.
01:12View SolutionA ball of mass `m` is distributed from the top of a fixed smooth circular tube in a vertical plane and falls impinging on a ball of mass `2 m` at the bottom. The coefficient of restitution is `1/2`. Find the heights to which the balls rise after a second impact.
View SolutionA particle of mass `1 kg` is attached to a string of length `5 m`. The string is attached to a fixed point `O`. It is released from the position as shown in Fig. Calculate
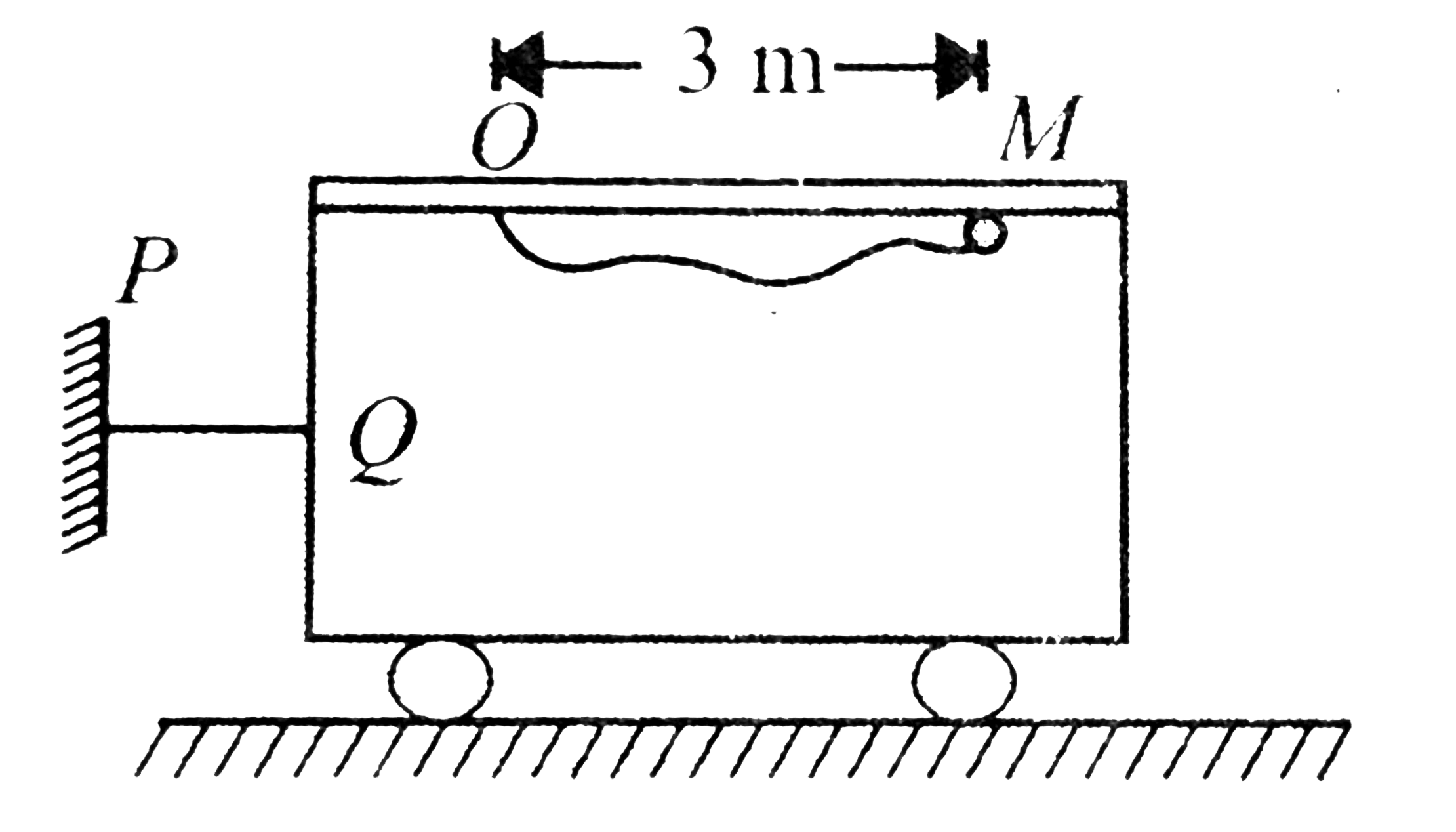
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string `PQ` at this instant.View SolutionA heavy ball of mass `2M` moving with a velocity `v_(0)` collides elastically head on with a cradle of three identical ball each of mass `M` as shown in figure. Determine the velocity of each ball after collision.
 View Solution
View SolutionIn Fig. there are `n` identical suspended with wires of equal length. The spheres are almost in contact with each other. Sphere `1` is pulled aside and released. If sphere `1` strikes sphere `2` with velocity `u`. find an expression for velocity `v_(n)` of the `nth` sphere immediately after being struck by the one adjacent to it. The coefficient of restitution for all the impacts is e.
 View Solution
View SolutionA smooth sphere of mass `m` is moving on a horizontal plane with a velocity `3hati+hatj` when it collides with a vertical wall which is parallel to the `hatj` vector. If the coefficient of restitution between the sphere and the wall is `1//2`. find
a. the velocity of the sphere after impact,
b. the loss in kinetic energy caused by the impact.
c. the impulse that acts on the sphere.View SolutionTwo smooth spheres. `A` and `B`. having equal radii, lie on a horizontal table. `A` is of mass `m` and `B` is of mass `3m`. The spheres are projected towards each other with velocity vector `5hati+2hatj` and `2hati-hatj`, respectively, and when they collide the lige joining their centres is parallel to the vector `hati`. If the coefficient of restitution between `A` and `B` is `1//3`, find the velocities after impact and the loss in kinetic energy caused by the collision. Find also the magnitude of the impulses that act at the instant of impact.
View SolutionA block `m_(1)` strikes a stationary block `m_(3)` inelastically. Another block `m_(2)` is kept on `m_(3)`. Neglecting the friction between all contacting surfaces, calculate the fractional decrease in `KE` of the system in collision.
View SolutionA mass `m_(1)` moves with a great velocity. It strikes another mass `m_(2)` at rest in head-on collision. It comes back along its path with low speed after collision. Then find out whether `m_(1)ltm _(2)` or `m_(1)gtm_(2)`.
02:59View SolutionA ball of mass `4 kg` moving with a velocity of `12 m//s` impinges directly on another ball of mass `8 kg` moving with velocity of `4 m//s` in the same direction. Find their velocities after impact and calculate the loss of `KE` due to impact if `e =0.5`.
02:28View SolutionA bullet of mass `2 g` travelling at a speed of `500 m//s` is fired into a ballistic pendulum of mass `1.0 kg` suspended from a cord `1.0 m` long. The bullet penetrates the pendulum and emerges with a velocity of `100 m//s`. Through what vertical height will the pendulum rise?
01:48View SolutionA `3.00 kg` steel hall strikes the wall with a speed of `10.0 m//s` at an angle of `60^(@)` with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for `0.200 s`, what is the average force exerted by the wall on the ball?
01:35View SolutionA spherical imperfectly elastic ball strikes a plane with velocity `8 m//s` at an angle of `30^(@)` with the plane. Determine the magnitude and direction of the velocity after impact if `e = 0.5` (neglect gravity).
 02:47View Solution
02:47View SolutionThree balls of masses `m_(1), m_(2)` and `m_(3)` are lying in a straight line. The first ball is moved with a certain velocity so that it strikes the second ball directly and itself comes to rest. The second ball collides with the third and is itself reduced to rest. If `e` is the coefficient of restitution for each ball, write down the relation of `m_(3)` in terms of `m_(1)` and `m_(2)`.
02:57View SolutionTwo identical balls `A` and `B` lie on a smooth horizontal surface, which gradually merges into a curve to a height `3.2 m`. Ball `A` is given a velocity of `10 m//s`, to collide head-on with ball `B`, which then takes up the curved path. What is the minimum coefficient of restitution, `e`, for the collision between `A` and `B` in order that ball `B` reaches the highest point `C` of the curve.
 03:01View Solution
03:01View SolutionA smooth ball of mass `m` is suspended from a light string of length `1 m`. Another ball of mass `2m` strikes the ball of mass in horizontally with a speed of `u=sqrt(35)m//s`. The coefficient of restitution for the collision is `e`. The string becomes loose, when it makes an angle of `30^(@)` with the horizontal, find the value of `e`.
 04:50View Solution
04:50View SolutionThree particles `A, B` and `C` of respective masses `m_(1), m_(2)` and `m_(3)` lie on a smooth horizontal surface, and an fastened to two light inextensible strings as shown in Fig. The particle `A` is imparted an impulse `J` along `vec(BA)` . Find the initial speed of each particle.
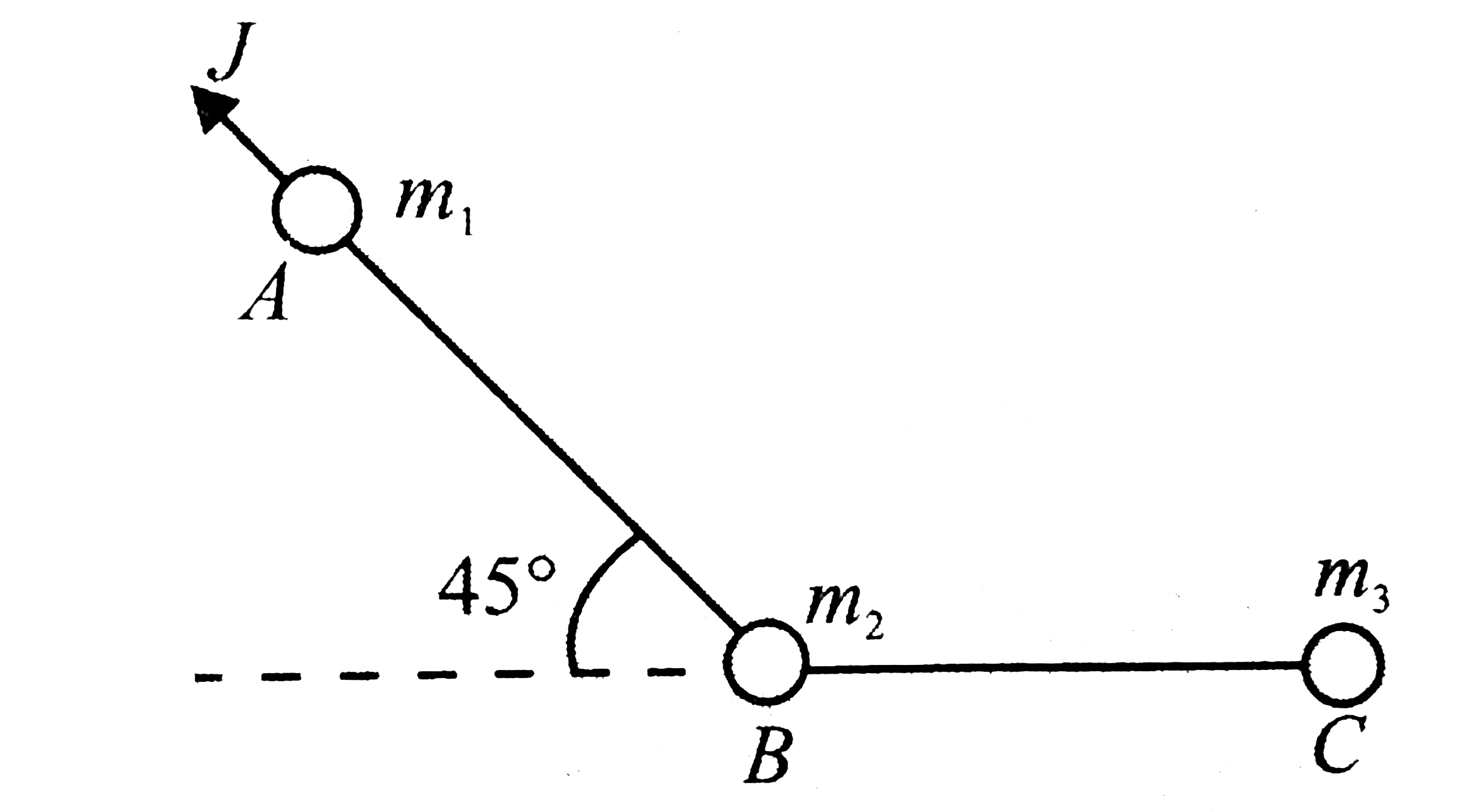 View Solution
View SolutionA ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is `theta`, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
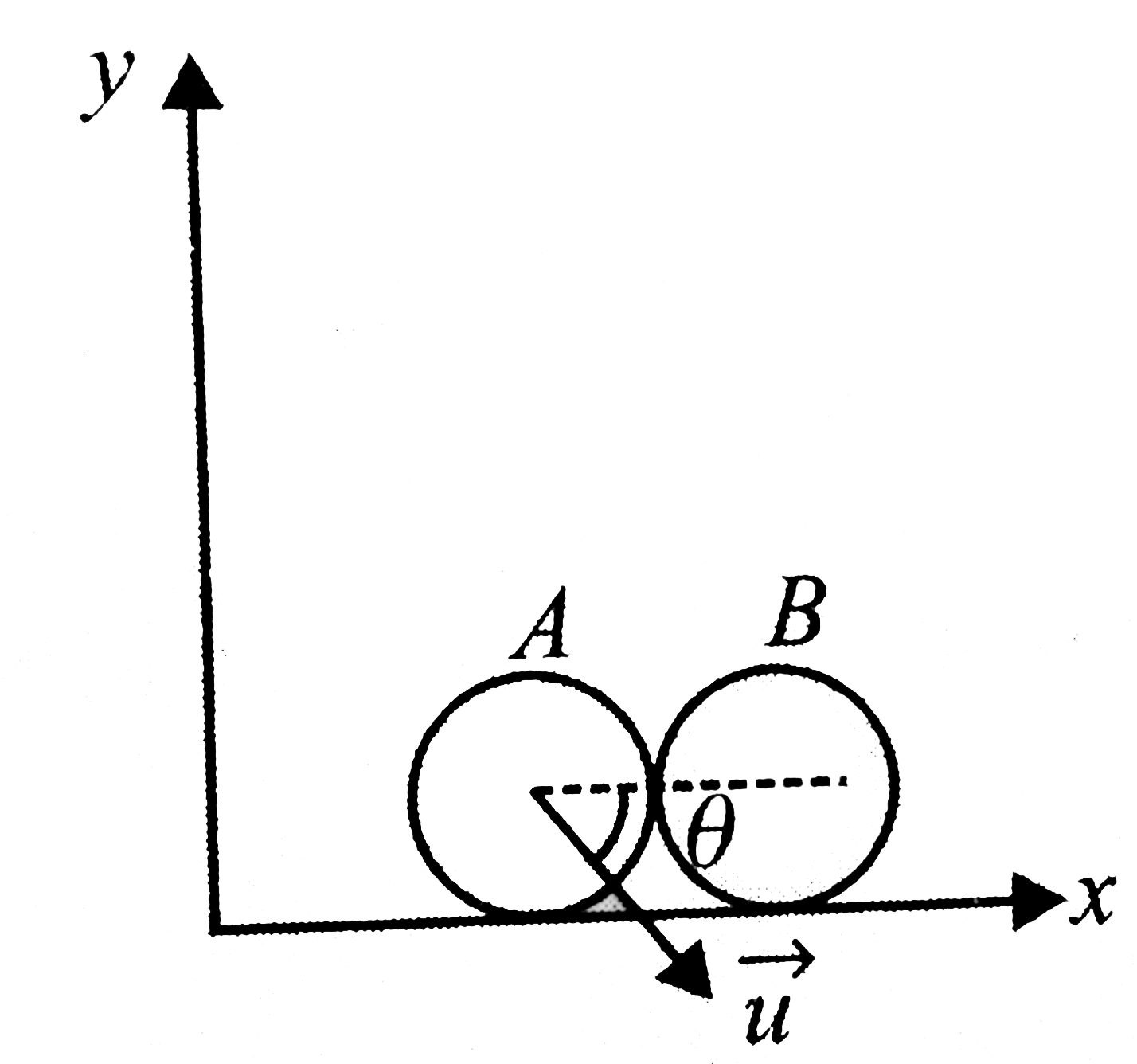 View Solution
View SolutionA machine gun can fire bullets of `50` grams at a Speed of `2000 m s^(-1)`, the man holding the gun can exert an average force of `200 N` against the gun. Calculate the maximum number of bullets which he can fire per minute.
01:35View SolutionA plate of mass `M` is held at rest by firing bullets from below. Each bullet has a mass `m`, velocity `u` (up) just before hitting and stops after hitting the plate for a moment and falls. Determine the number of bullets striking the plate Fig. per unit time
 01:17View Solution
01:17View SolutionA steel ball is suspended by a light in extensible string of length l from a fixed point `O`. When the ball is in equilibrium it just touches a vertical wall as shown in the figure. The ball is first taken aside such that string becomes horizontal and then released from rest. If coefficient of restitution is e, then find the maximum deflection of the string after `nth` collision.
 02:51View Solution
02:51View SolutionA smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane.
a. If `e = 0`, find the speed of the ball just after leaving the inclined plane 1.
b. If the particle mioves horizontally just after the collision find `e`.
 View Solution
View SolutionA small particle of mass `m` is released from a height `h` on a large smooth sphere kept on a perfectly smooth surface as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.
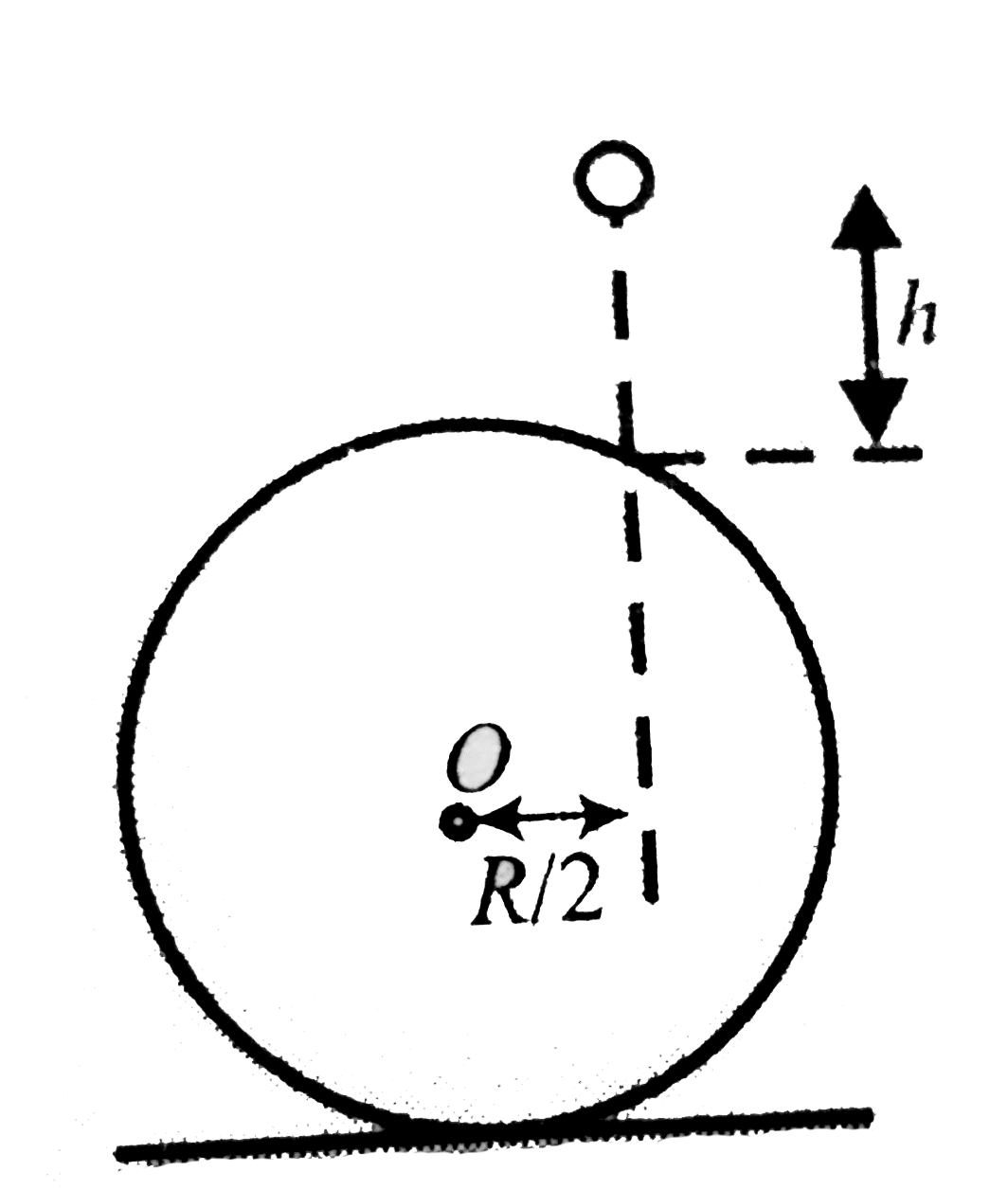 View Solution
View Solution
Exercise 1.3 questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11
