Complete Solutions to Linked Comprehension of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| CENGAGE PHYSICS | Linked Comprehension |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Three spheres, each of mass `m`, can slide freely on a frictionless, horizontal surface. Spheres `A` and `B` are attached to an inextensible, inelastic cord of length `l` and are at rest in the position shown where sphere `B` is struck by sphere `C` which is moving to the right with a velocity `v_(0)`. Knowing that the cord is taut where sphere `B` is struck by sphere `C` and assuming 'head on' inelastic impact between `B` and `C`, we cannot conserve kinetic energy of the entire system.
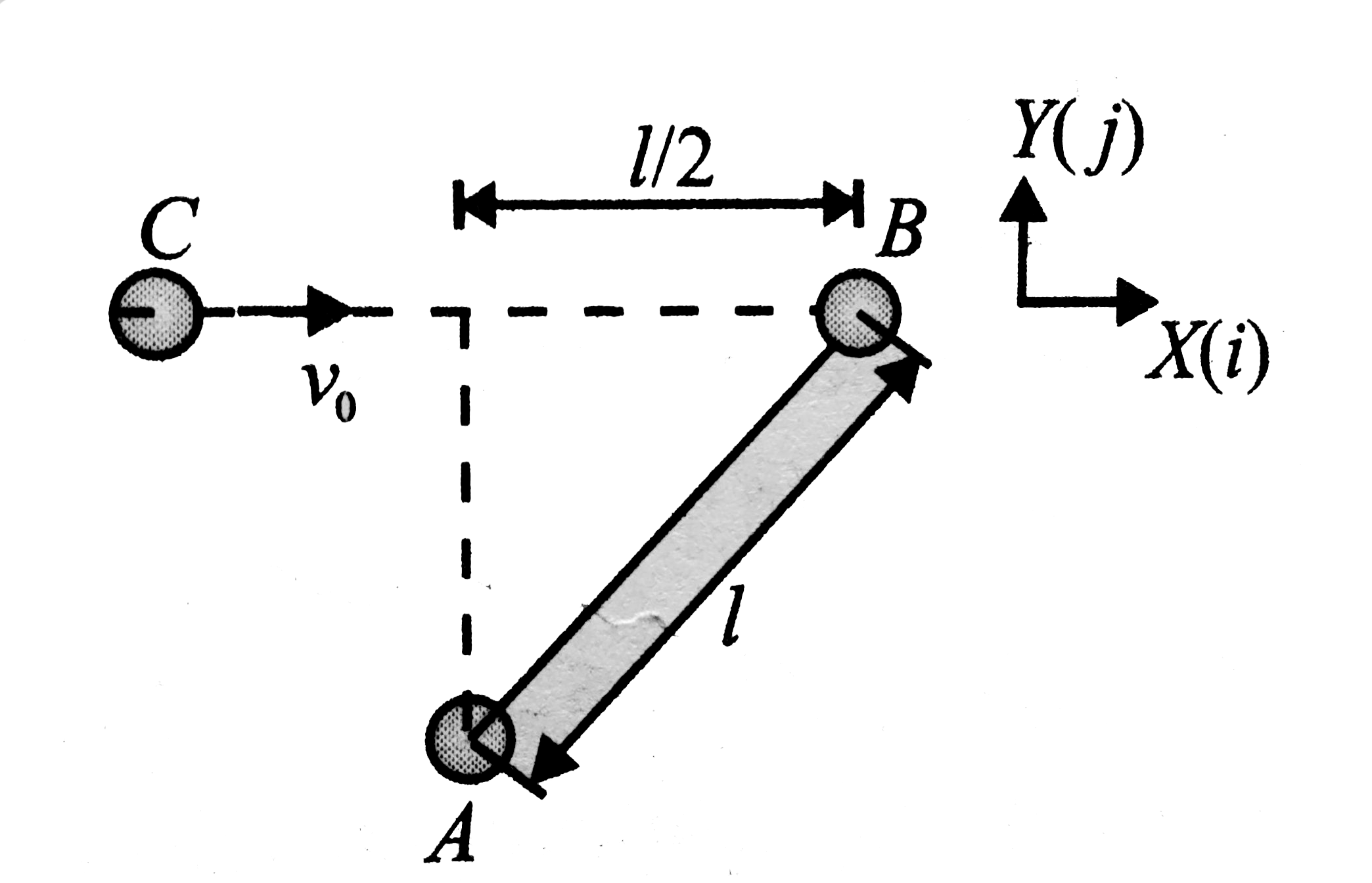 Velocity of `A` immediately after collision is along unit vector View Solution
Velocity of `A` immediately after collision is along unit vector View SolutionThree spheres, each of mass `m`, can slide freely on a frictionless, horizontal surface. Spheres `A` and `B` are attached to an inextensible, inelastic cord of length `l` and are at rest in the position shown where sphere `B` is struck by sphere `C` which is moving to the right with a velocity `v_(0)`. Knowing that the cord is taut where sphere `B` is struck by sphere `C` and assuming 'head on' inelastic impact between `B` and `C`, we cannot conserve kinetic energy of the entire system.
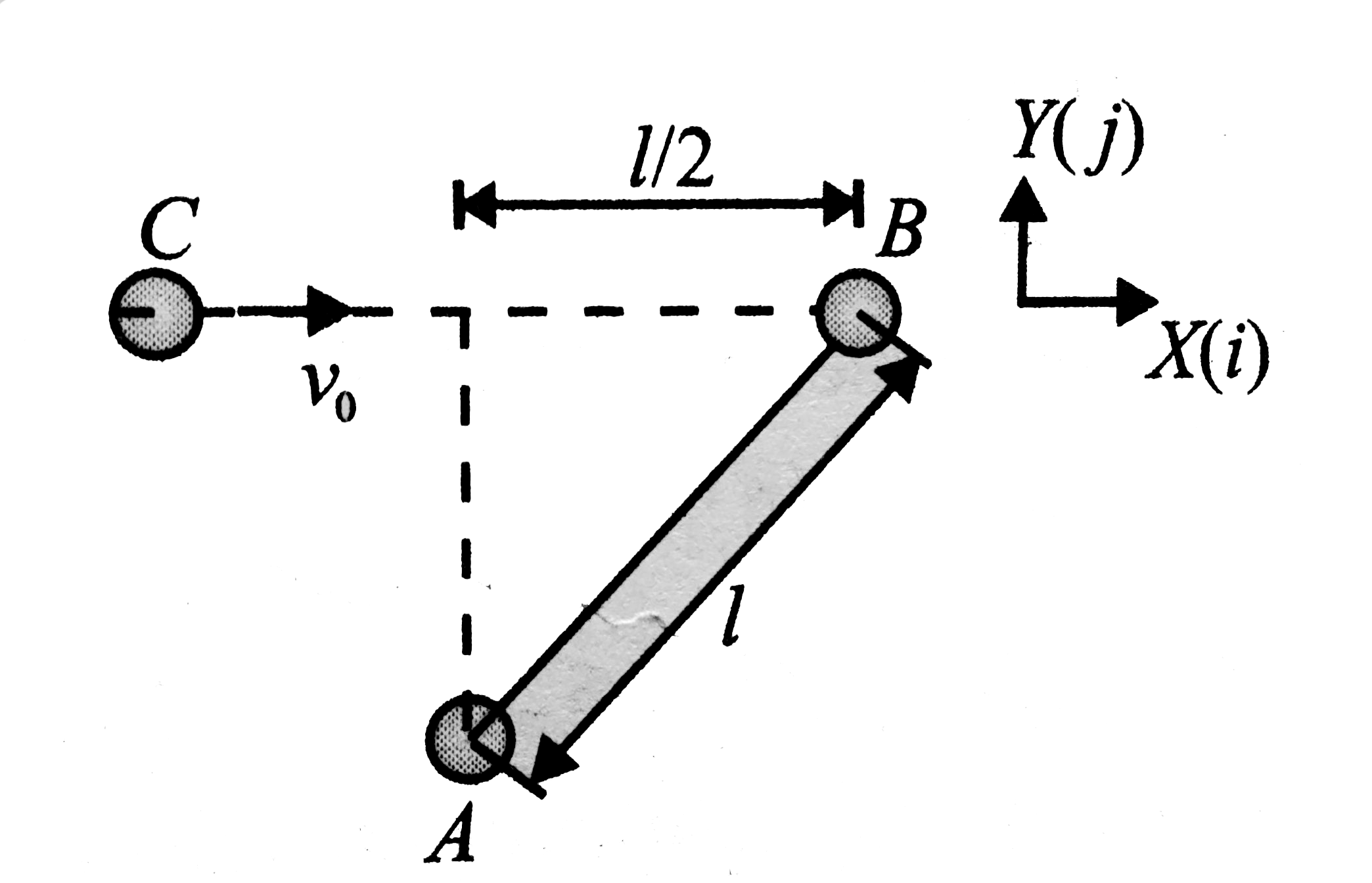
If velocity of `C` immediately after collision becomes `(v_(0))/2` in the initial direction of motion, the impulse due to string on sphere `A` isView SolutionThree spheres, each of mass `m`, can slide freely on a frictionless, horizontal surface. Spheres `A` and `B` are attached to an inextensible, inelastic cord of length `l` and are at rest in the position shown where sphere `B` is struck by sphere `C` which is moving to the right with a velocity `v_(0)`. Knowing that the cord is taut where sphere `B` is struck by sphere `C` and assuming 'head on' inelastic impact between `B` and `C`, we cannot conserve kinetic energy of the entire system.
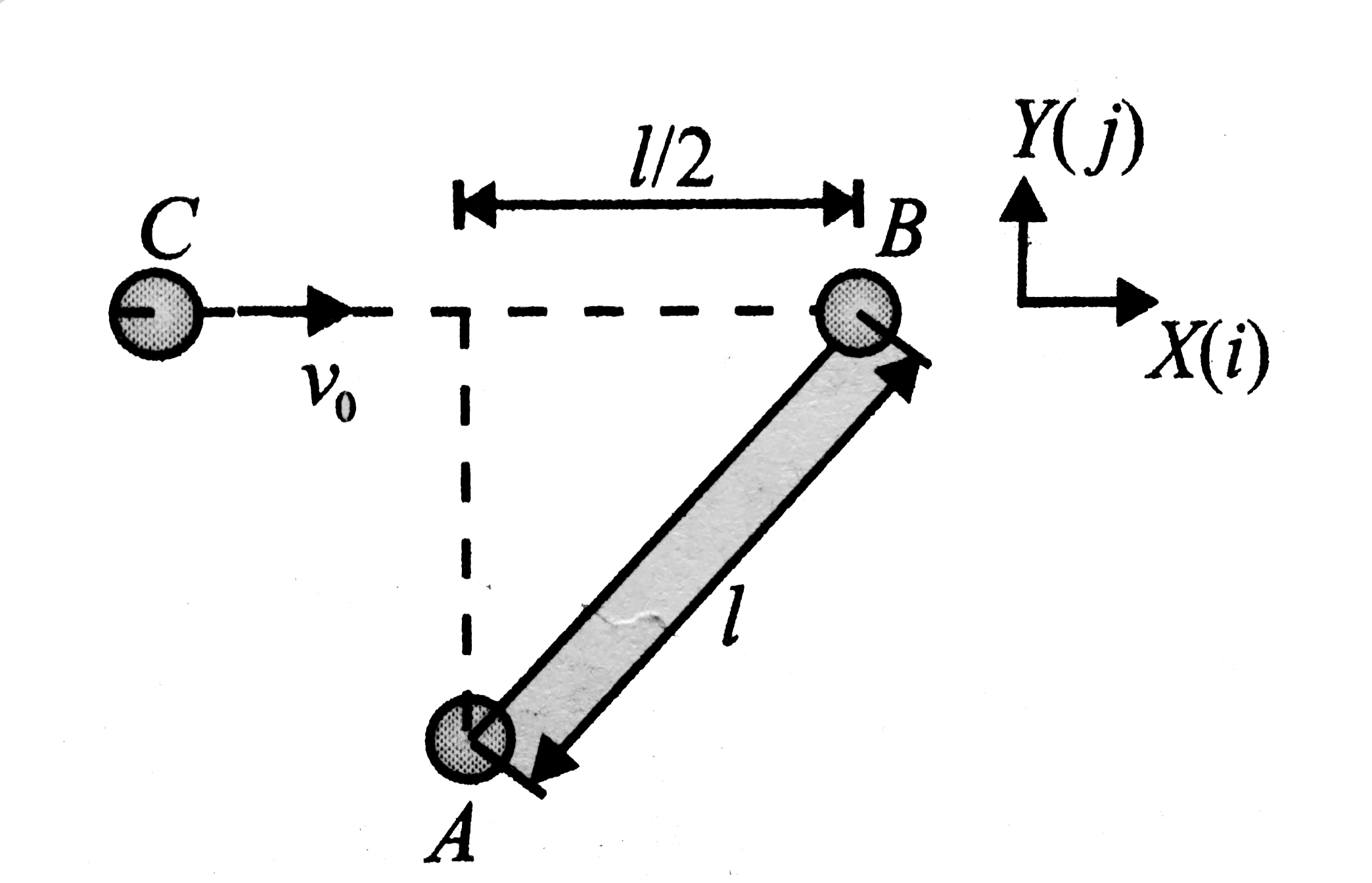
The magnitude of velocity of `A` immediately after collision isView SolutionThree spheres, each of mass `m`, can slide freely on a frictionless, horizontal surface. Spheres `A` and `B` are attached to an inextensible, inelastic cord of length `l` and are at rest in the position shown where sphere `B` is struck by sphere `C` which is moving to the right with a velocity `v_(0)`. Knowing that the cord is taut where sphere `B` is struck by sphere `C` and assuming 'head on' inelastic impact between `B` and `C`, we cannot conserve kinetic energy of the entire system.
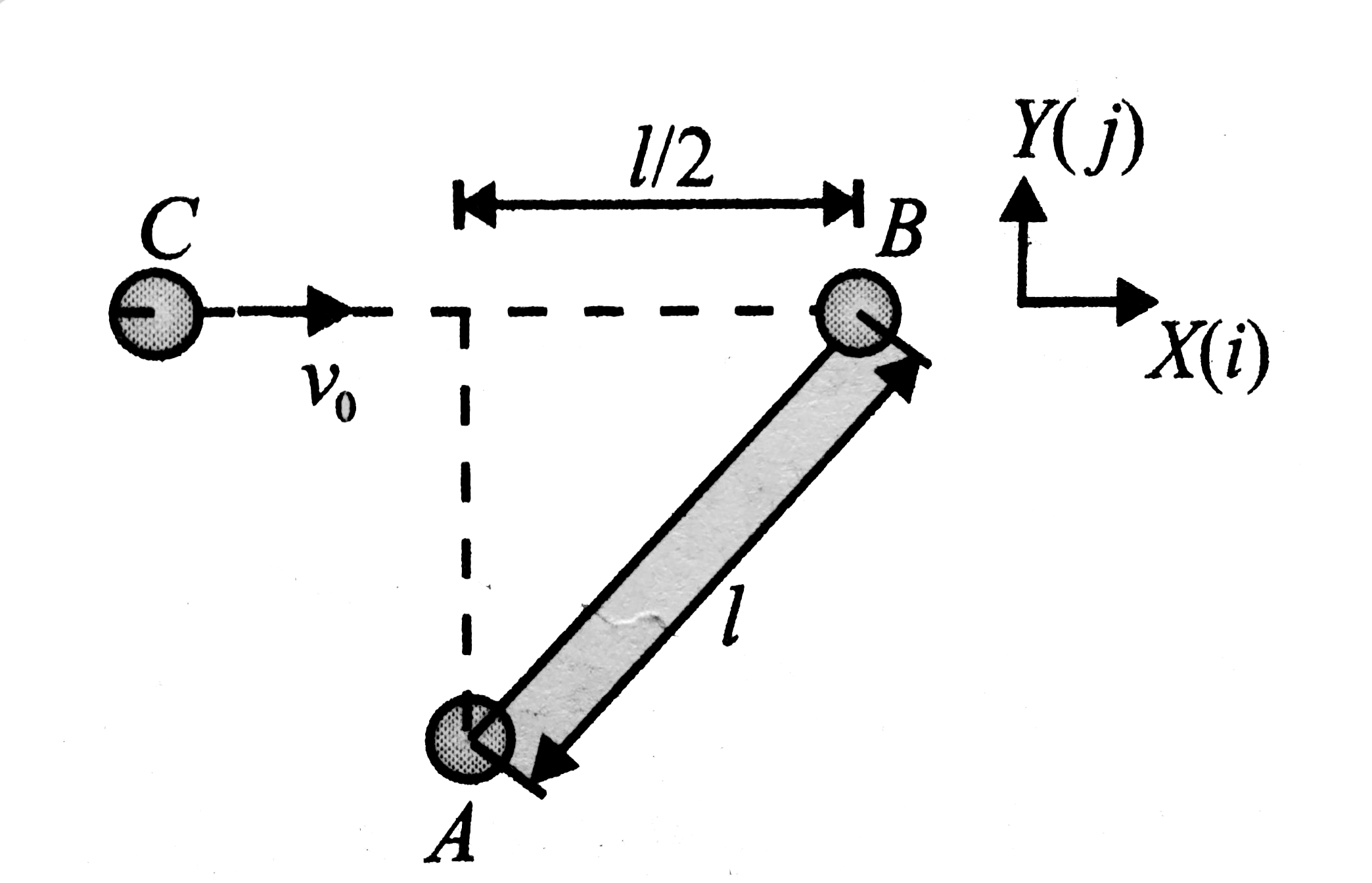
The loss is kinetic energy of the system during collision isView SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of collision in paragraph I, which of the following physical process is not a collision?09:59View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
For which of the following collisions, the external force acting on the system during collision is not appreciable as mentioned in paragraph 1.09:59View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of oblique collision in the paragraph, which of the following collisions cannot be oblique'?09:59View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
Which of the following collisions is one-dimensional?09:59View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
A `4 kg` sphere moving with a velocity of `4 m//s` collides with an identical sphere of `2 kg` moving with `2 m//s` as shown. Final kinetic energy is less than initial kinetic energy. What type of collision is this?
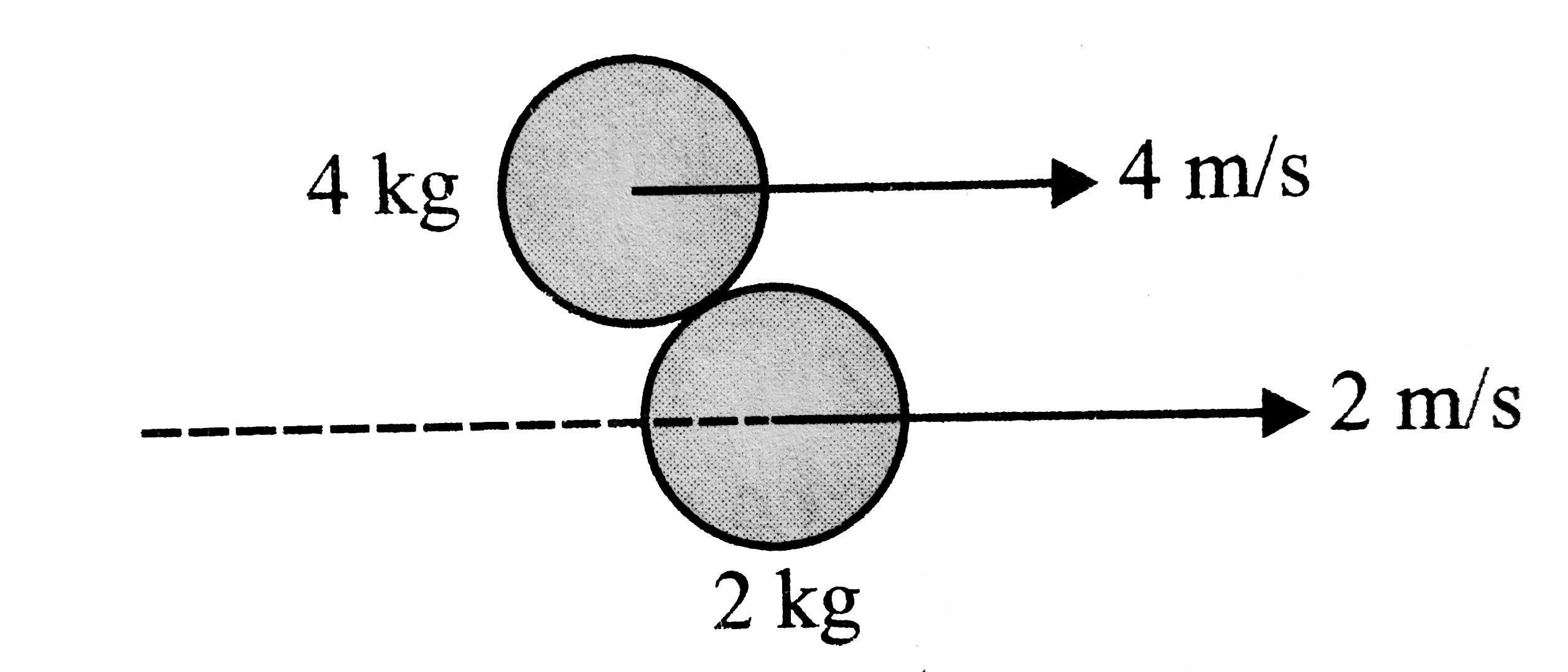 09:59View Solution
09:59View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass `M` is placed on a smooth horizontal surface. light identical springs, each of stiffness `K`, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is `3l`. A block of mass `m` is placed on the plank and pressed against one of the springs so that it is compressed to `l`. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
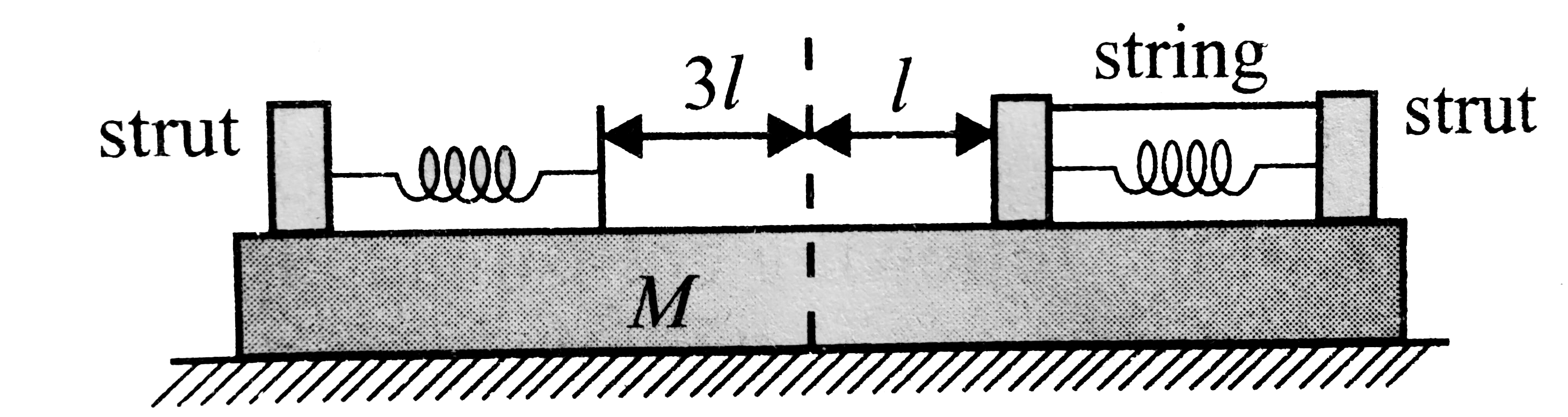
The maximum displacement of the plank is04:52View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass `M` is placed on a smooth horizontal surface. light identical springs, each of stiffness `K`, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is `3l`. A block of mass `m` is placed on the plank and pressed against one of the springs so that it is compressed to `l`. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

The maximum velocity of the plank is04:52View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass `M` is placed on a smooth horizontal surface. light identical springs, each of stiffness `K`, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is `3l`. A block of mass `m` is placed on the plank and pressed against one of the springs so that it is compressed to `l`. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
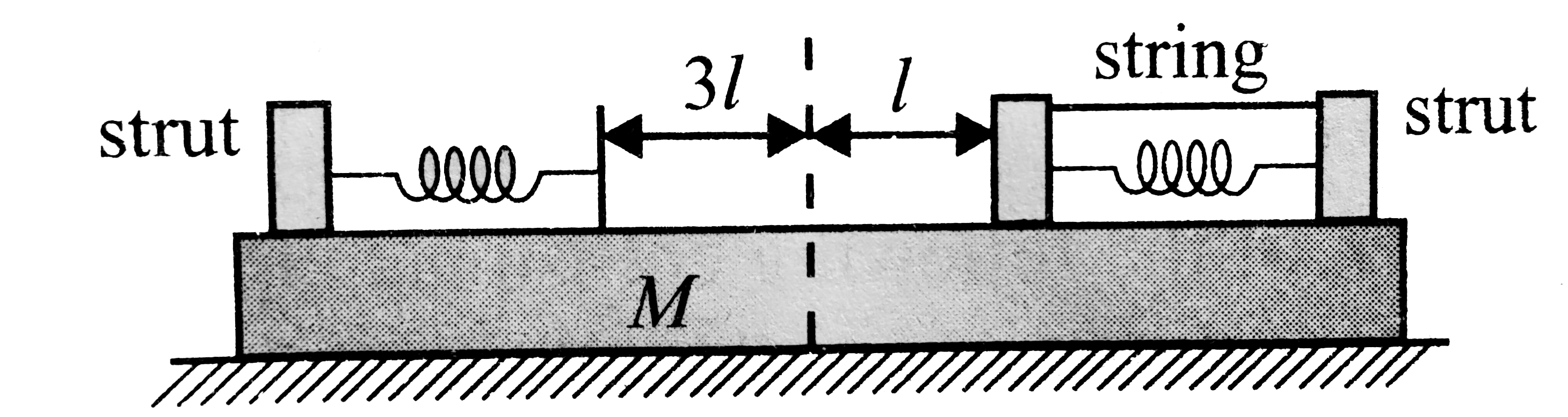
The maximum kinetic energy of the block `m` is04:52View SolutionTwo identical balls `A` and `B`. each of mass `2 kg` and radius `R`, are suspended vertically from inextensible strings as shown in Fig. The third ball `C` of mass `1 kg` and radius `r=(sqrt(2)-1)R` falls and hits `A` and `B` symmetrically with `10 m//s`. Speed of both `A` and `B` just after the collision is `3 m//s`.
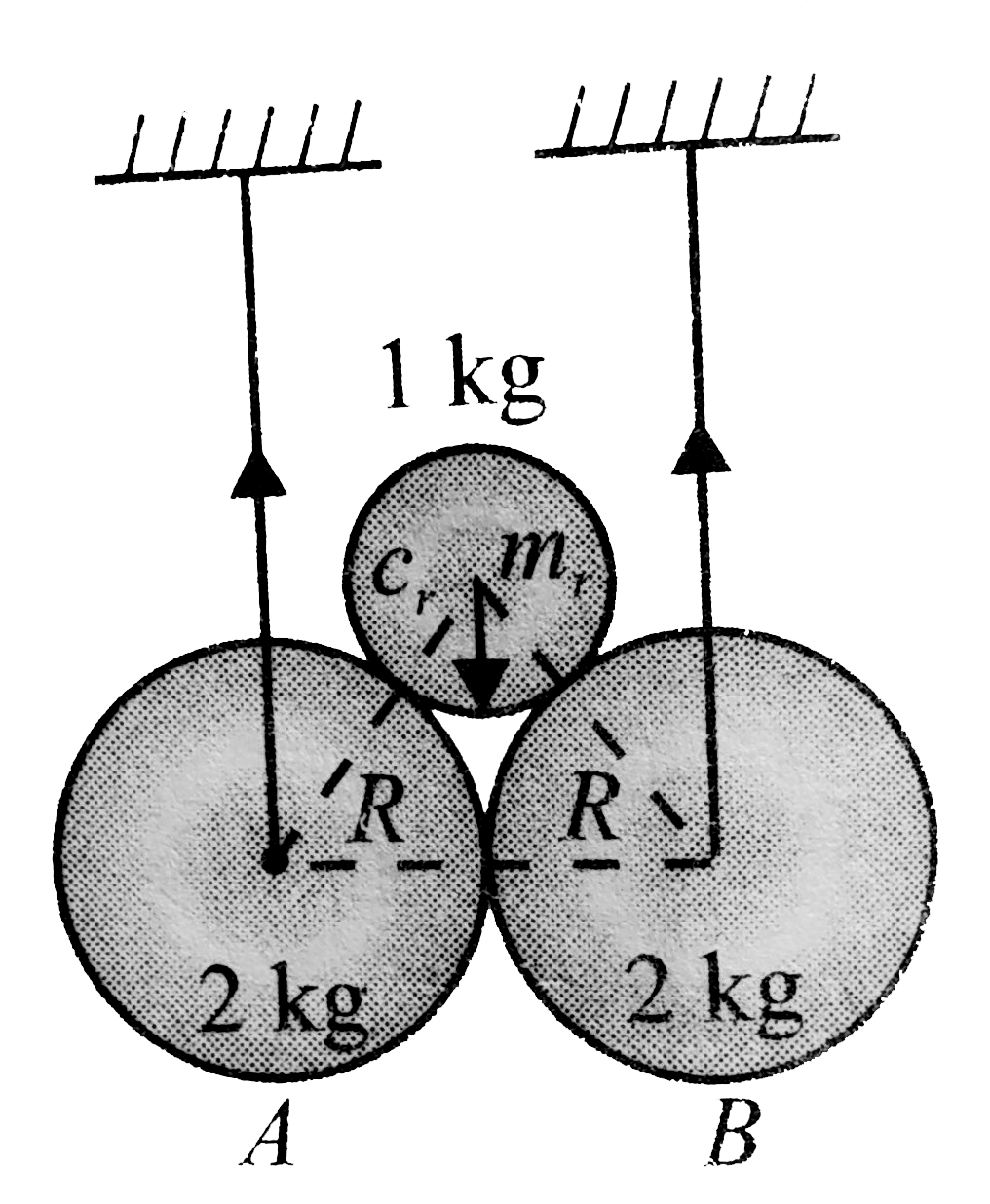
speed of `C` just asfter collision isView SolutionTwo identical balls `A` and `B`. each of mass `2 kg` and radius `R`, are suspended vertically from inextensible strings as shown in Fig. The third ball `C` of mass `1 kg` and radius `r=(sqrt(2)-1)R` falls and hits `A` and `B` symmetrically with `10 m//s`. Speed of both `A` and `B` just after the collision is `3 m//s`.
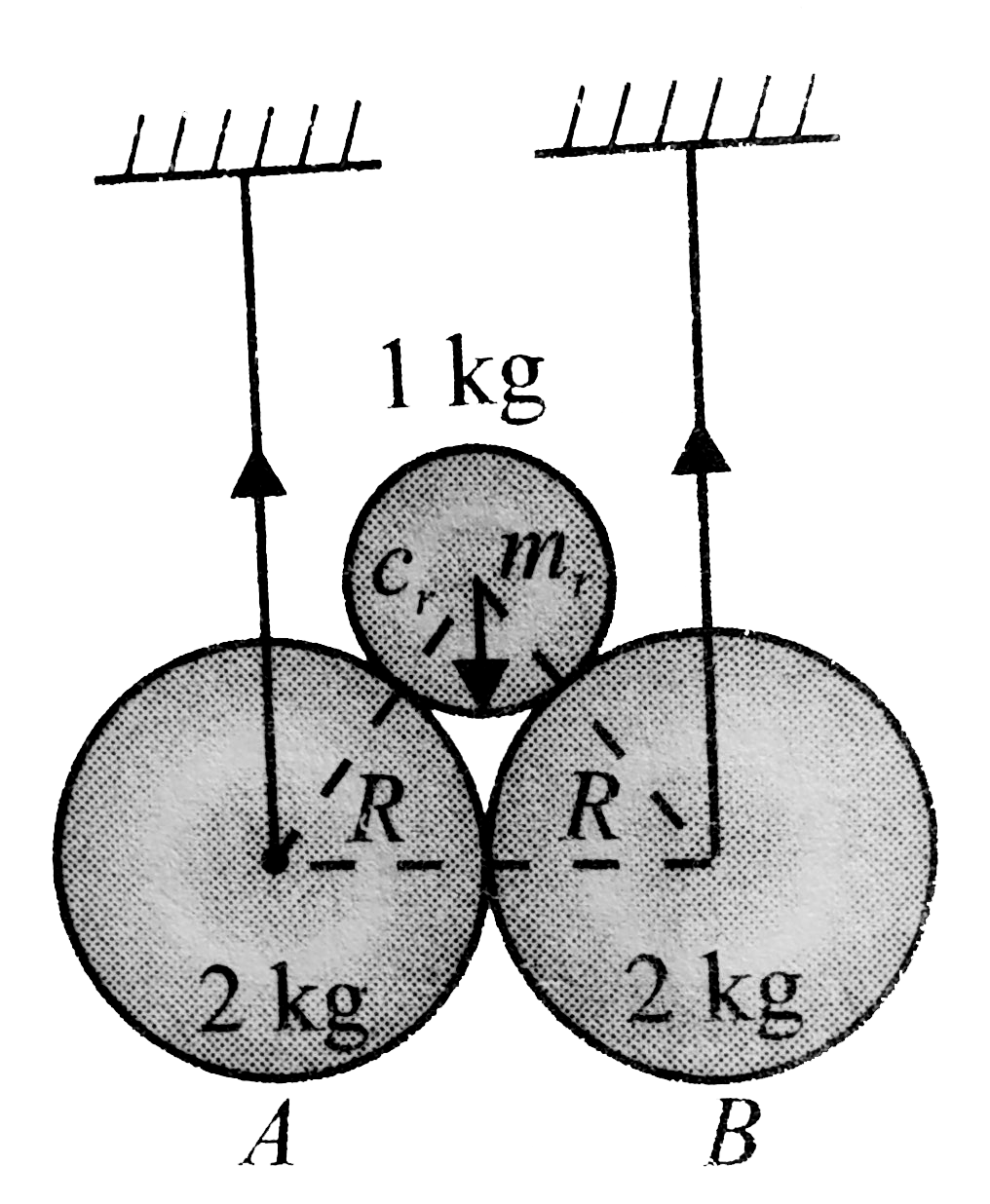
Impulse provided by each sting during collision isView SolutionTwo identical balls `A` and `B`. each of mass `2 kg` and radius `R`, are suspended vertically from inextensible strings as shown in Fig. The third ball `C` of mass `1 kg` and radius `r=(sqrt(2)-1)R` falls and hits `A` and `B` symmetrically with `10 m//s`. Speed of both `A` and `B` just after the collision is `3 m//s`.
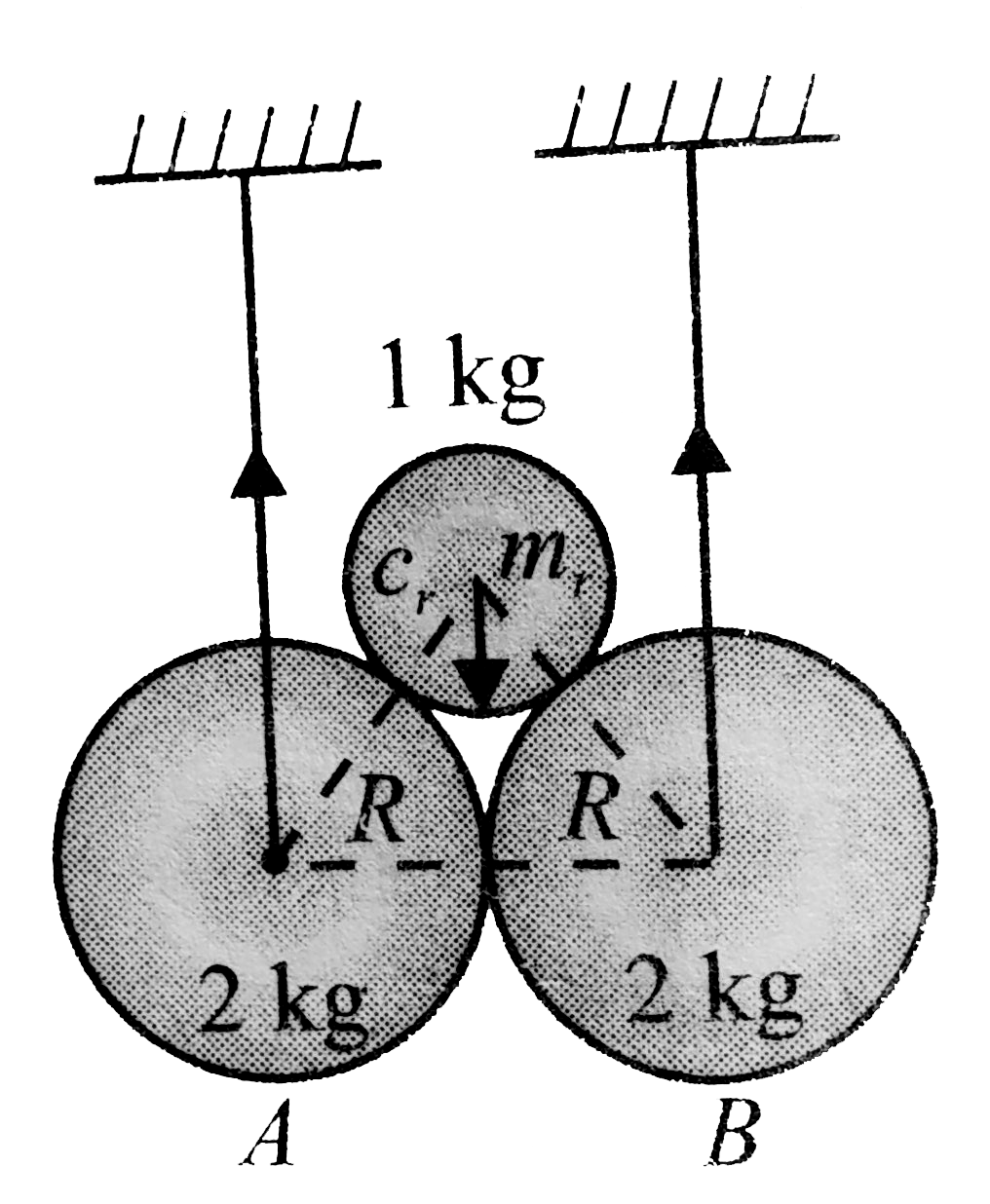
The value of coefficient of restitution isView SolutionAfter falling from rest through a height `h`, a body of mass `m` begins to raise a body of mass `M (M gt m)` connected to it through a pulley. Determnethe time it will take for the body of mass `M` to return to its original position
02:52View SolutionAfter falling from rest through a height `h`, a body of mass `m` begins to raise a body of mass `M (M gt m)` connected to it through a pulley.
Find the fraction of kinetic energy lost when the body of mass `M` is jerked into motion04:07View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is `l`.
At moment `t = 0`, ball `B` is imparted a velocity `v_(0)` perpendicular to the strings and then the system is left on its own.

Calculate the velocity of `B` just before `A` collides with ball `C`.04:28View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is `l`.
At moment `t = 0`, ball `B` is imparted a velocity `v_(0)` perpendicular to the strings and then the system is left on its own.

Calculate the velocity of `A` at the above given instant.03:37View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is `l`.
At moment `t = 0`, ball `B` is imparted a velocity `v_(0)` perpendicular to the strings and then the system is left on its own.

If collision between the balls is completely inelastic, then03:37View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass `m` can slide on the string without any friction. One end of the string is attached to point `B` and to the other end, a block `'P'` of mass `m` is attached. The whole system lies in vertical plane.
 If the system is released from rest, it is found that the system remains at rest. What is the value of `theta`05:37View Solution
If the system is released from rest, it is found that the system remains at rest. What is the value of `theta`05:37View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass `m` can slide on the string without any friction. One end of the string is attached to point `B` and to the other end, a block `'P'` of mass `m` is attached. The whole system lies in vertical plane.
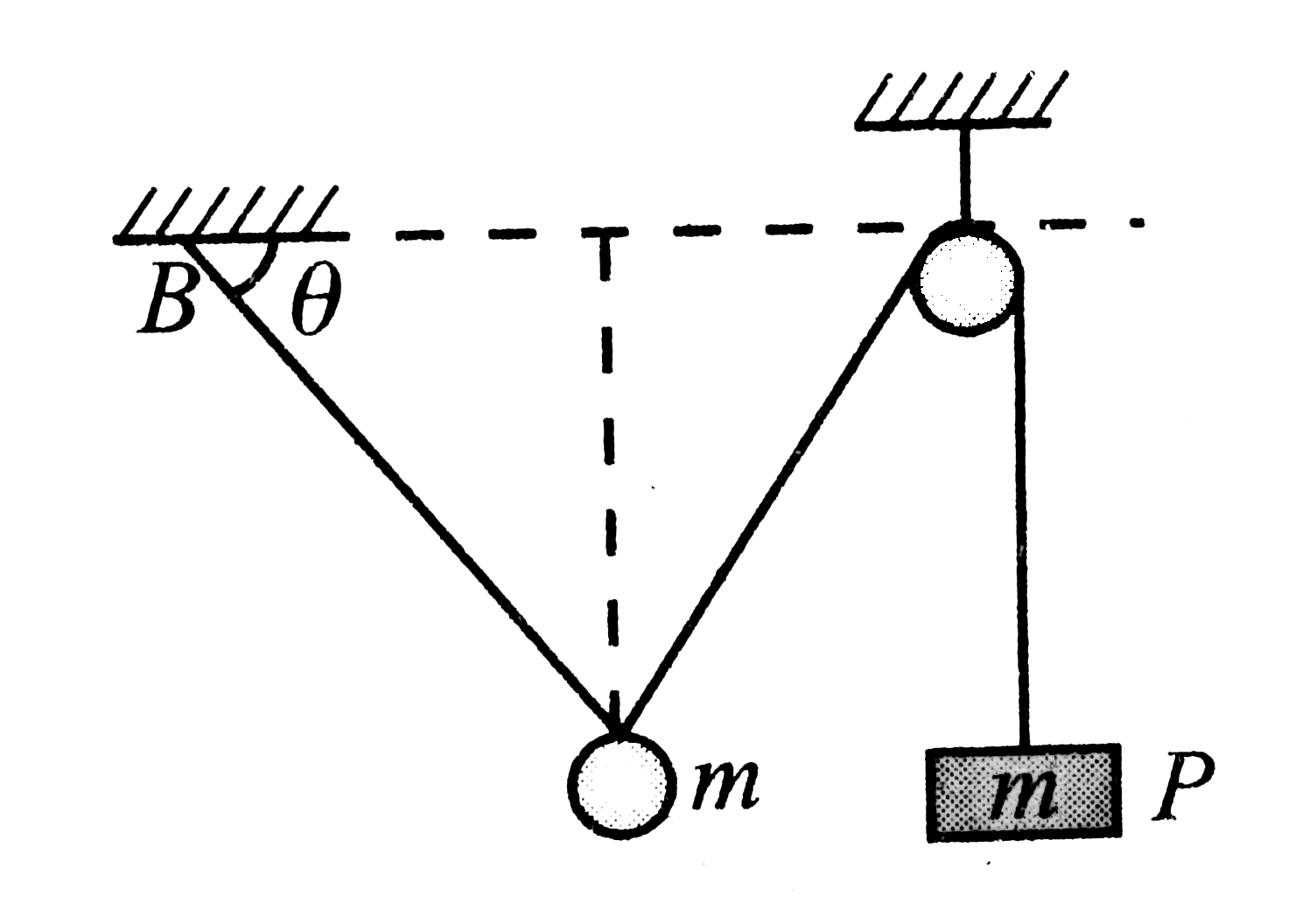 Now another block `'C'` of same mass `m` is attached to the block `'13'` and system is released from rest. If `a_(1)` and `a_(2)` are the magnitudes of initial accelerations of ring and blocks, respectively, then 05:37View Solution
Now another block `'C'` of same mass `m` is attached to the block `'13'` and system is released from rest. If `a_(1)` and `a_(2)` are the magnitudes of initial accelerations of ring and blocks, respectively, then 05:37View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass `m` can slide on the string without any friction. One end of the string is attached to point `B` and to the other end, a block `'P'` of mass `m` is attached. The whole system lies in vertical plane.
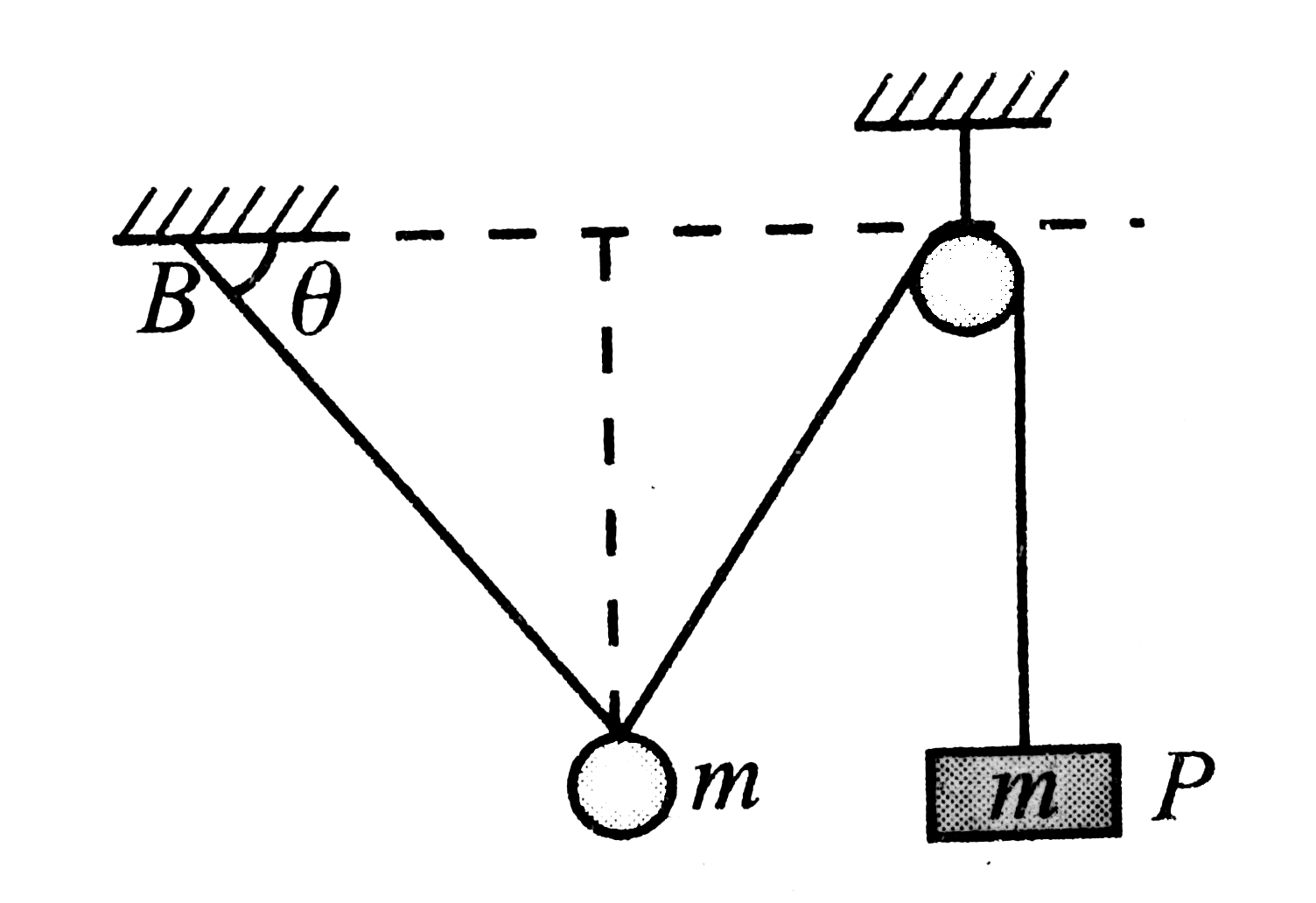 If block `'C'` mentioned above was released from some height and collided with `'P'` with some velocity `u`, then find the velocity of the ring just after the collision. The collision is perfectly inelastic. 05:37View Solution
If block `'C'` mentioned above was released from some height and collided with `'P'` with some velocity `u`, then find the velocity of the ring just after the collision. The collision is perfectly inelastic. 05:37View SolutionA system of men and trolley is shown in Fig. To the left, end of the string, a trolley of mass `M` is connected on which a man of mass `m` is standing. To the right end of the string another trolley of mass `m` is connected on which a man of mass `M` is standing. Initially, the system is at rest. All of a sudden both the men leap upwards simultaneously with the same velocity `u` w.r.t. ground.

Find the relative velocity of left man with respect to his trolley just after he leaps upwards.05:28View SolutionA system of men and trolley is shown in Fig. To the left, end of the string, a trolley of mass `M` is connected on which a man of mass `m` is standing. To the right end of the string another trolley of mass `m` is connected on which a man of mass `M` is standing. Initially, the system is at rest. All of a sudden both the men leap upwards simultaneously with the same velocity `u` w.r.t. ground.

Find the impulse generated in the string connecting the trolleys during this process.05:28View SolutionA system of men and trolley is shown in Fig. To the left, end of the string, a trolley of mass `M` is connected on which a man of mass `m` is standing. To the right end of the string another trolley of mass `m` is connected on which a man of mass `M` is standing. Initially, the system is at rest. All of a sudden both the men leap upwards simultaneously with the same velocity `u` w.r.t. ground.

Which is correct05:28View SolutionTwo beads `A` and `B` of masses `m_(1)` and `m_(2)` respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. `B` is stationary at the lowest point when `A` is gently dislodged from rest at the highest point. A collided with `B` at the lowest point. The impulse given to `B` due to collision is just great enough to carry it to the level of the centre of the circle while `A` is immediately brought to rest by the impact.

Find the ratio `m_(1):m_(2)`08:44View SolutionTwo beads `A` and `B` of masses `m_(1)` and `m_(2)` respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. `B` is stationary at the lowest point when `A` is gently dislodged from rest at the highest point. A collided with `B` at the lowest point. The impulse given to `B` due to collision is just great enough to carry it to the level of the centre of the circle while `A` is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?08:44View Solution
What is the coefficient of restituting between the beads?08:44View SolutionTwo beads `A` and `B` of masses `m_(1)` and `m_(2)` respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. `B` is stationary at the lowest point when `A` is gently dislodged from rest at the highest point. A collided with `B` at the lowest point. The impulse given to `B` due to collision is just great enough to carry it to the level of the centre of the circle while `A` is immediately brought to rest by the impact.

If `m_(2)` again comes down and collides with `m_(1)` then after the collision08:44View SolutionTwo blocks of equal mass `m` are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force `F` is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time `t` is05:58View SolutionTwo blocks of equal mass `m` are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force `F` is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is `x_(0)` at time `t`, then the displacement of the first block at this instant is05:58View SolutionTwo blocks of equal mass `m` are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force `F` is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is `x_(0)` at time `t`, then the displacement of the second block at this instant is05:58View SolutionTwo equal spheres `B` and `C`, each of mass `m`, are in contact on a smooth horizontal table. A third sphere `A` of same size as that of `B` or `C` but mass `m//2` impinges symmetrically on them with a velocity `u` and is itself brought to rest.
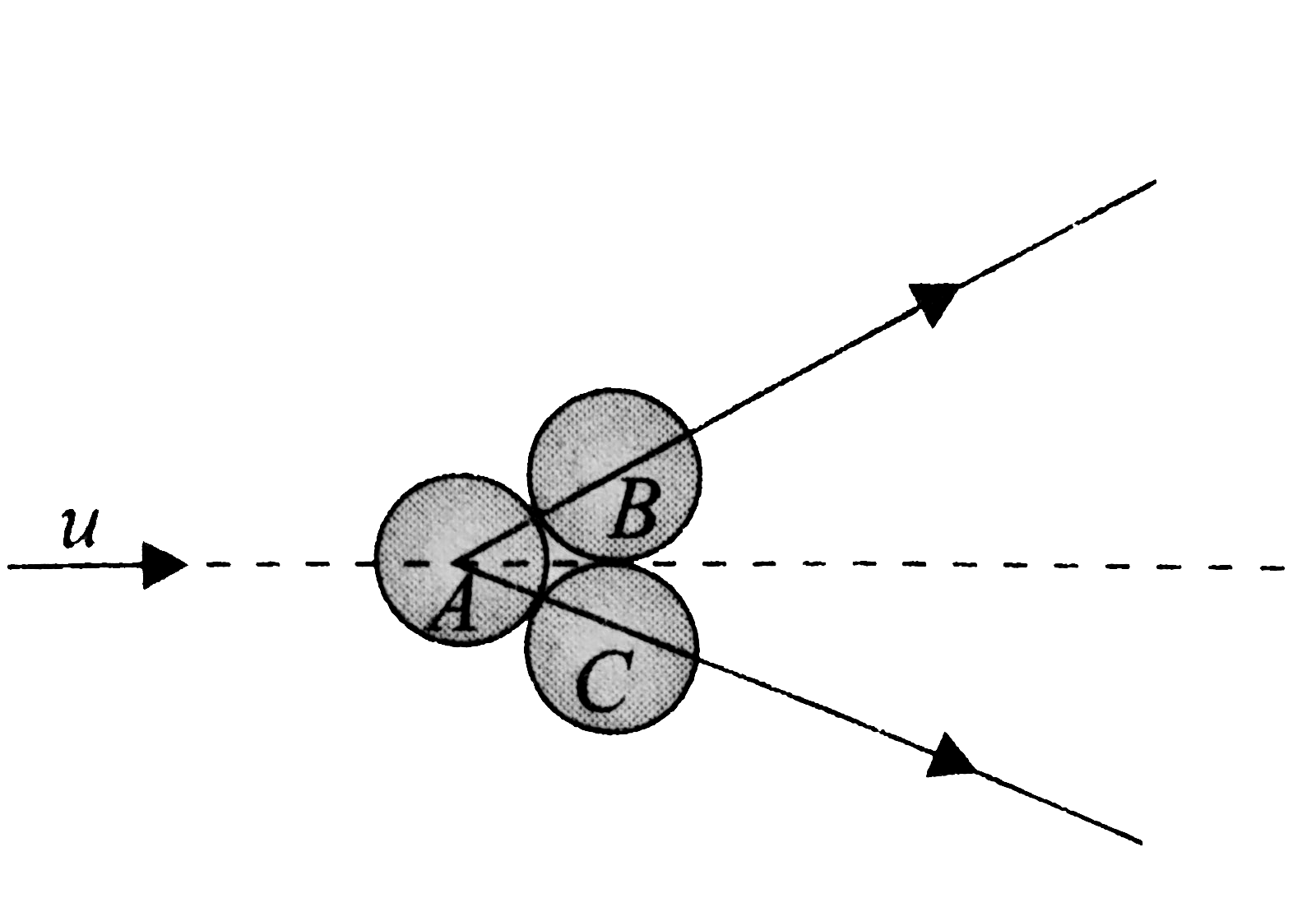
The coefficient of restitution between the two spheres `A` and `B` (or between `A` and `C`) isView SolutionTwo equal spheres `B` and `C`, each of mass `m`, are in contact on a smooth horizontal table. A third sphere `A` of same size as that of `B` or `C` but mass `m//2` impinges symmetrically on them with a velocity `u` and is itself brought to rest.
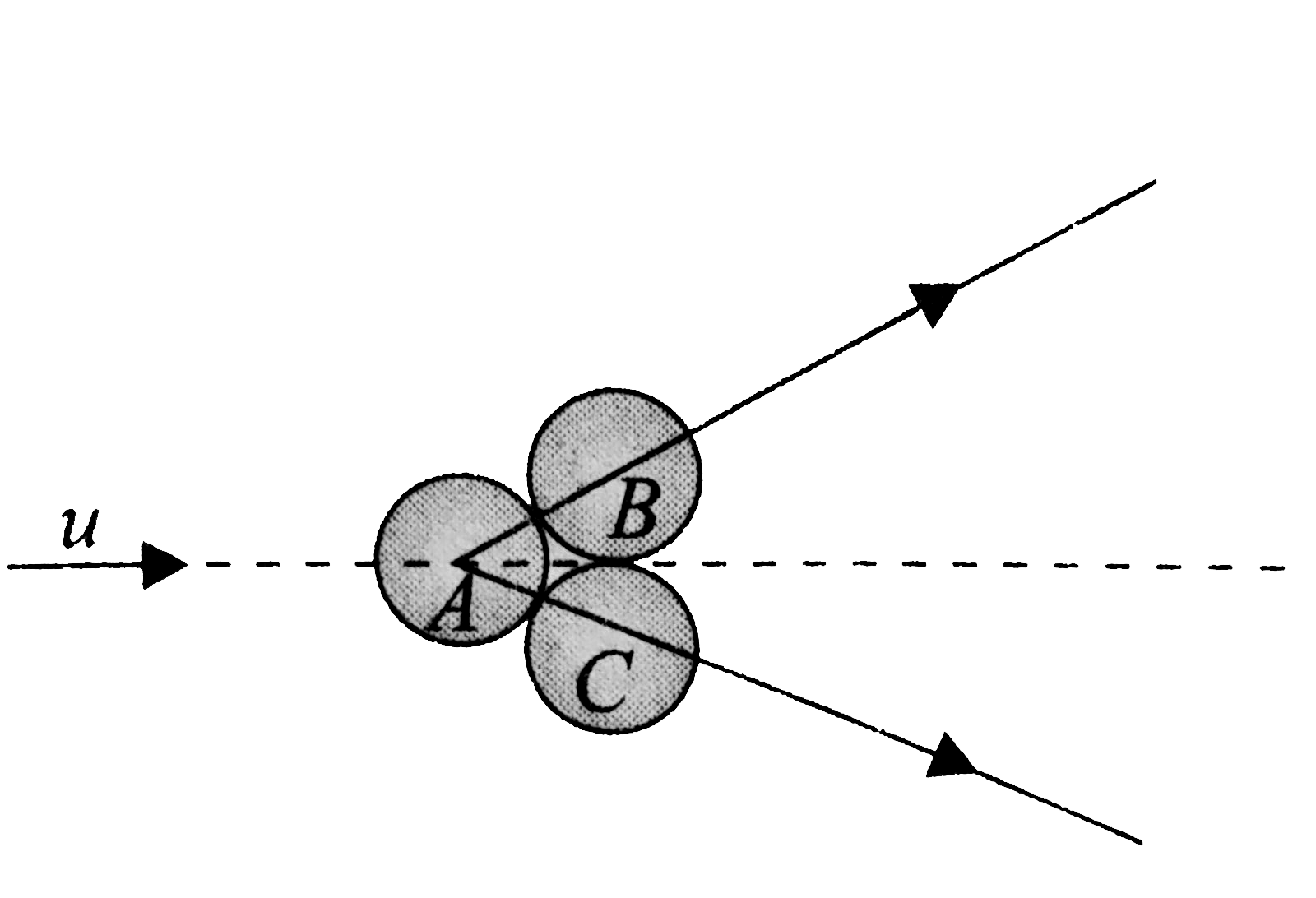
Find the velocity acquired by each of the spheres B and C after collision.View SolutionTwo equal spheres `B` and `C`, each of mass `m`, are in contact on a smooth horizontal table. A third sphere `A` of same size as that of `B` or `C` but mass `m//2` impinges symmetrically on them with a velocity `u` and is itself brought to rest.
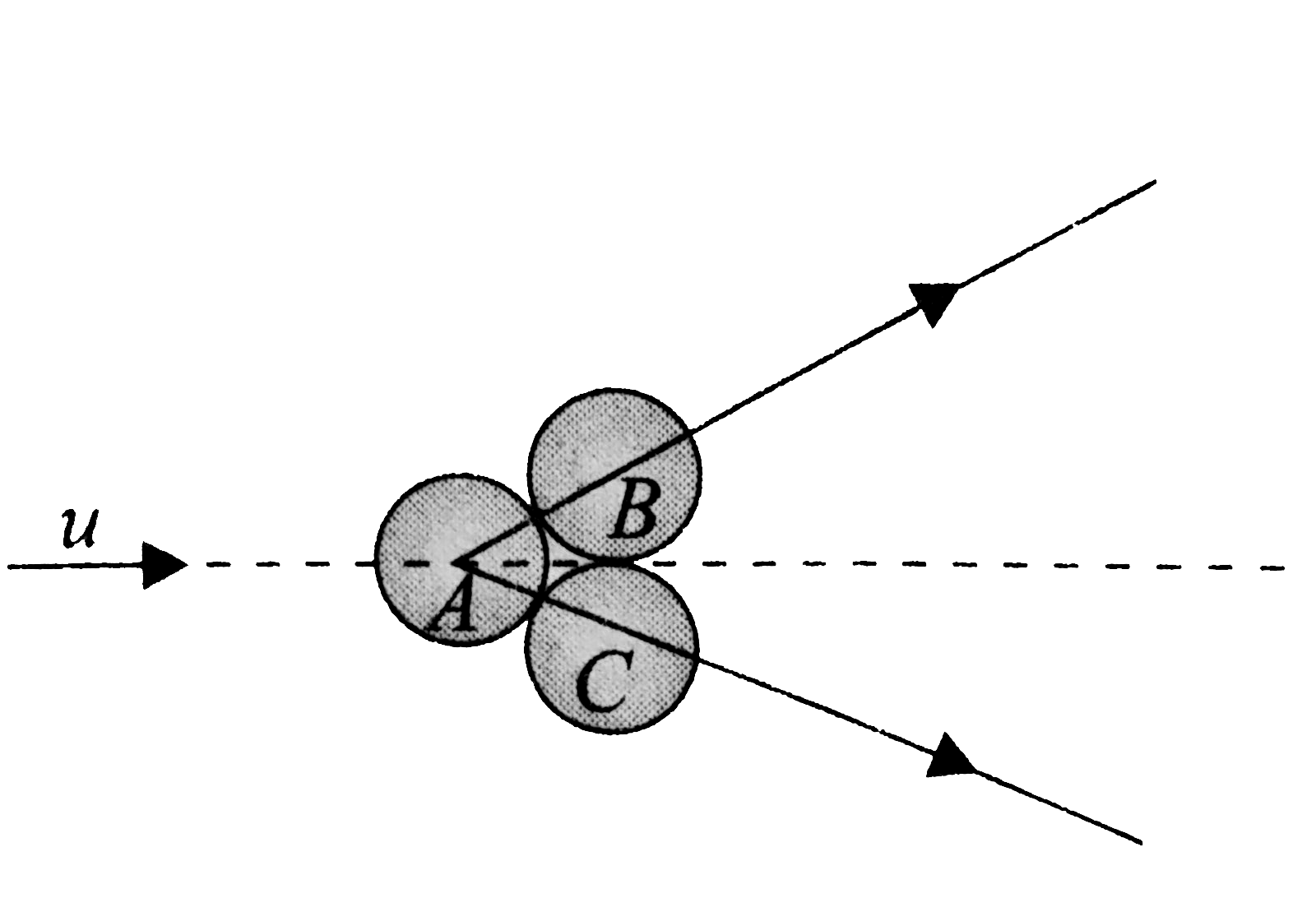
The loss of `KE` during collision isView SolutionA pendulum consists of a wooden bob of mass `M` and length `l`. A bullet of mass `m` is fired towards the pendulum with a speed `v`. The bullet emerges immediately out of the bob from the other side with a speed of `v//2` and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
What is the momentum transferred to the bob by the bullet?06:13View SolutionA pendulum consists of a wooden bob of mass `M` and length `l`. A bullet of mass `m` is fired towards the pendulum with a speed `v`. The bullet emerges immediately out of the bob from the other side with a speed of `v//2` and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob stops where the string becomes horizontal then `v` is06:13View SolutionA pendulum consists of a wooden bob of mass `M` and length `l`. A bullet of mass `m` is fired towards the pendulum with a speed `v`. The bullet emerges immediately out of the bob from the other side with a speed of `v//2` and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob is just able to complete the circular motion, then tension at the lowest point just when the bob starts rising will be06:13View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses `'m'`and `'2m'` are placed as shown in Fig. There is no friction anywhere. A spring of force constant `k` is attached to the bigger block. Mass `'m'` is kept in touch with the spring but not attached to it. `'A'` and `'B'` are two supports attached to `'2m'`. Now `m` is moved towards left so that spring is compressed by distance `'x'` and then the system is released from rest.

Find the relative velocity of the blocks after `'m'` leaves contact with the spring.View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses `'m'`and `'2m'` are placed as shown in Fig. There is no friction anywhere. A spring of force constant `k` is attached to the bigger block. Mass `'m'` is kept in touch with the spring but not attached to it. `'A'` and `'B'` are two supports attached to `'2m'`. Now `m` is moved towards left so that spring is compressed by distance `'x'` and then the system is released from rest.

Now `m` arrives at `B`. Due to its inertia of motion `'m'` breaks the support `'B'` and due to some resistance offered by `'B'` , the resulting velocity of `'m'` is reduced to half of its previous value. Then what you can say about the velocity of `2m`?View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses `'m'`and `'2m'` are placed as shown in Fig. There is no friction anywhere. A spring of force constant `k` is attached to the bigger block. Mass `'m'` is kept in touch with the spring but not attached to it. `'A'` and `'B'` are two supports attached to `'2m'`. Now `m` is moved towards left so that spring is compressed by distance `'x'` and then the system is released from rest.

What is the loss in the energy of the system due to breaking of `B`?View SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass `M`, hanging from two long cords. A bullet of mass `m` is fired into the block. the bullet comes quickly into rest and the block `+` bullet rises to a vertical distance `h` before the pendulum comes momentarily to rest as the ends of the arc. ltbr. In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

After collision what is the combined velocity of the bullet `+` block system?View SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass `M`, hanging from two long cords. A bullet of mass `m` is fired into the block. the bullet comes quickly into rest and the block `+` bullet rises to a vertical distance `h` before the pendulum comes momentarily to rest as the ends of the arc. ltbr. In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

What is the initial speed of the bullet in terms of height `h`?View SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass `M`, hanging from two long cords. A bullet of mass `m` is fired into the block. the bullet comes quickly into rest and the block `+` bullet rises to a vertical distance `h` before the pendulum comes momentarily to rest as the ends of the arc. ltbr. In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

The collision of block-bullet system isView SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass `M`, hanging from two long cords. A bullet of mass `m` is fired into the block. the bullet comes quickly into rest and the block `+` bullet rises to a vertical distance `h` before the pendulum comes momentarily to rest as the ends of the arc. ltbr. In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

The energy dissipated as heat in the collision isView SolutionTwo identical balls, each of mass `m`, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities `2u` and `u`. in the same direction. Collision between the balls is perfectly elastic.

After the first collision, what is the total loss in kinetic energy of the balls?View SolutionTwo identical balls, each of mass `m`, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities `2u` and `u`. in the same direction. Collision between the balls is perfectly elastic.

What is the final in kinetic energy of the balls?View SolutionTwo identical balls, each of mass `m`, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities `2u` and `u`. in the same direction. Collision between the balls is perfectly elastic.

What is the impulse generated in the string during the second collision?View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass `250 g` is thrown with a speed of `30 m//s`. The ball strikes a bat and it is hit straight back along the same line at a speed of `50 m//s`. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
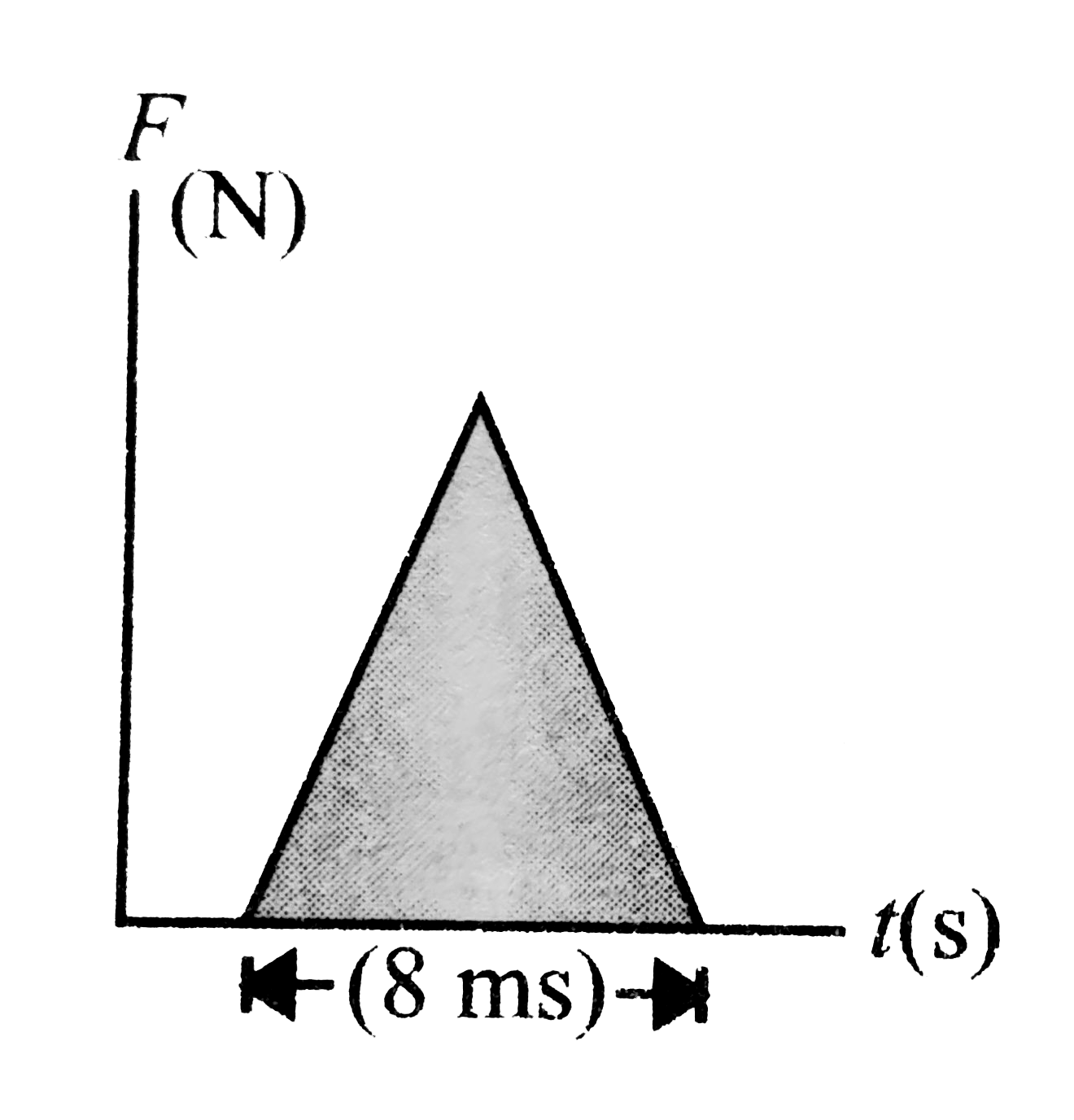
Maximum force exerted by the bat on the ball is05:47View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass `250 g` is thrown with a speed of `30 m//s`. The ball strikes a bat and it is hit straight back along the same line at a speed of `50 m//s`. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
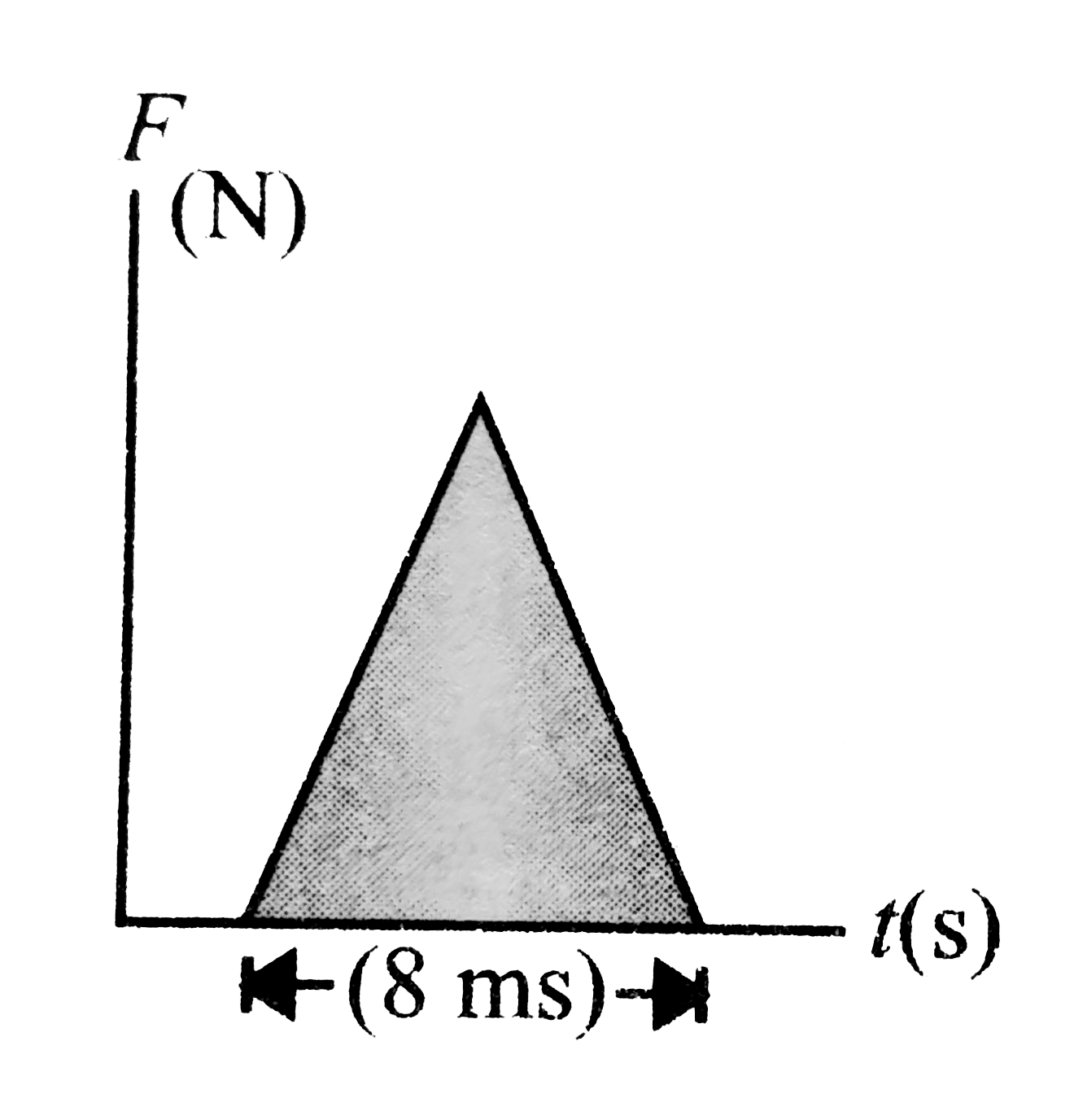
Average force exerted by the bat on the ball is
Let us consider another example. The given ball of mass `250 g` is dropped from a height `5 m` on a hard floor. Force exerted by the floor on the ball, as long as these are in contact, varies with time as shown in Fig.
 05:47View Solution
05:47View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass `250 g` is thrown with a speed of `30 m//s`. The ball strikes a bat and it is hit straight back along the same line at a speed of `50 m//s`. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
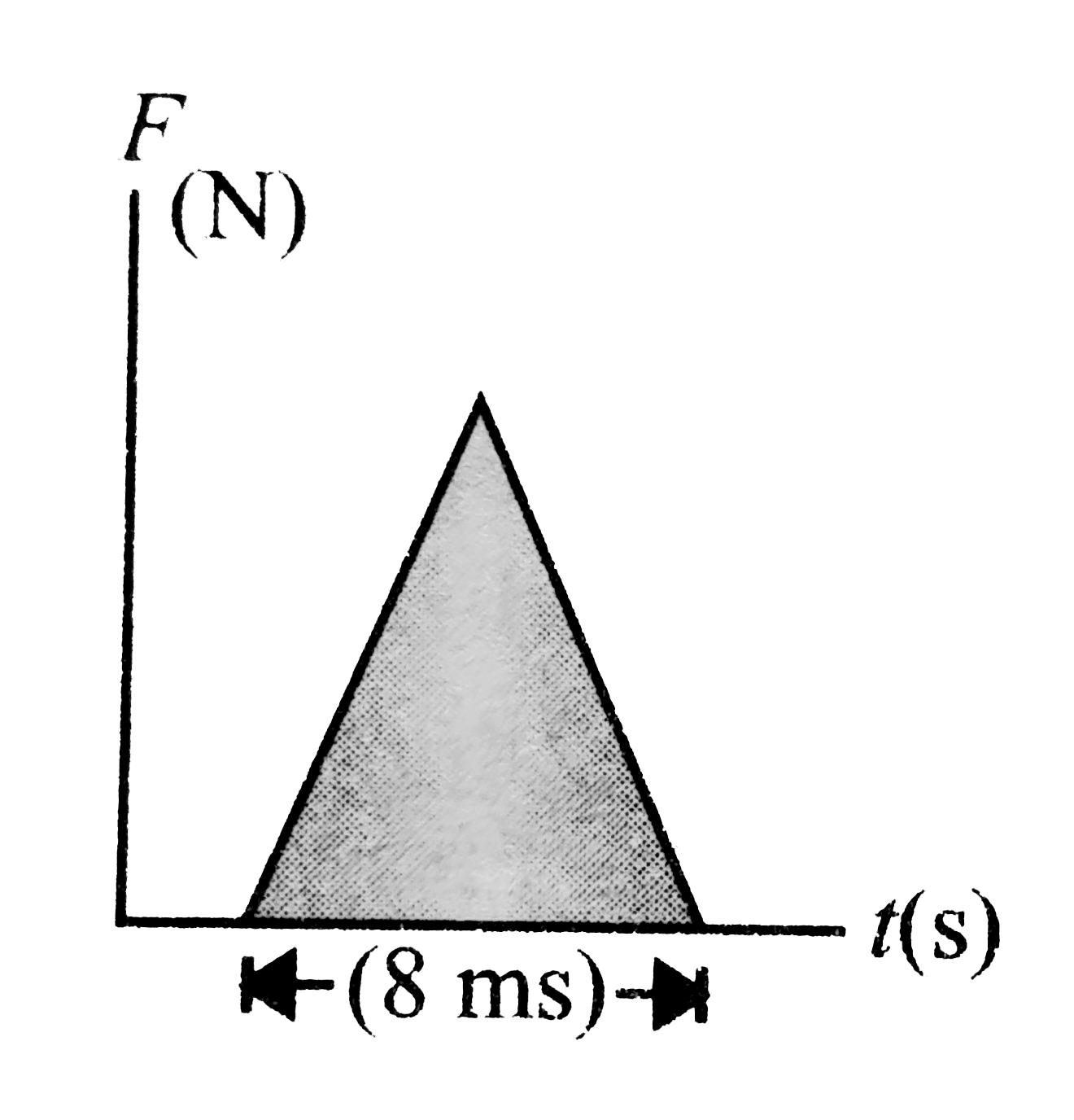
Linear momentum of the ball immediately after colliding with the floor will be05:47View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass `250 g` is thrown with a speed of `30 m//s`. The ball strikes a bat and it is hit straight back along the same line at a speed of `50 m//s`. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
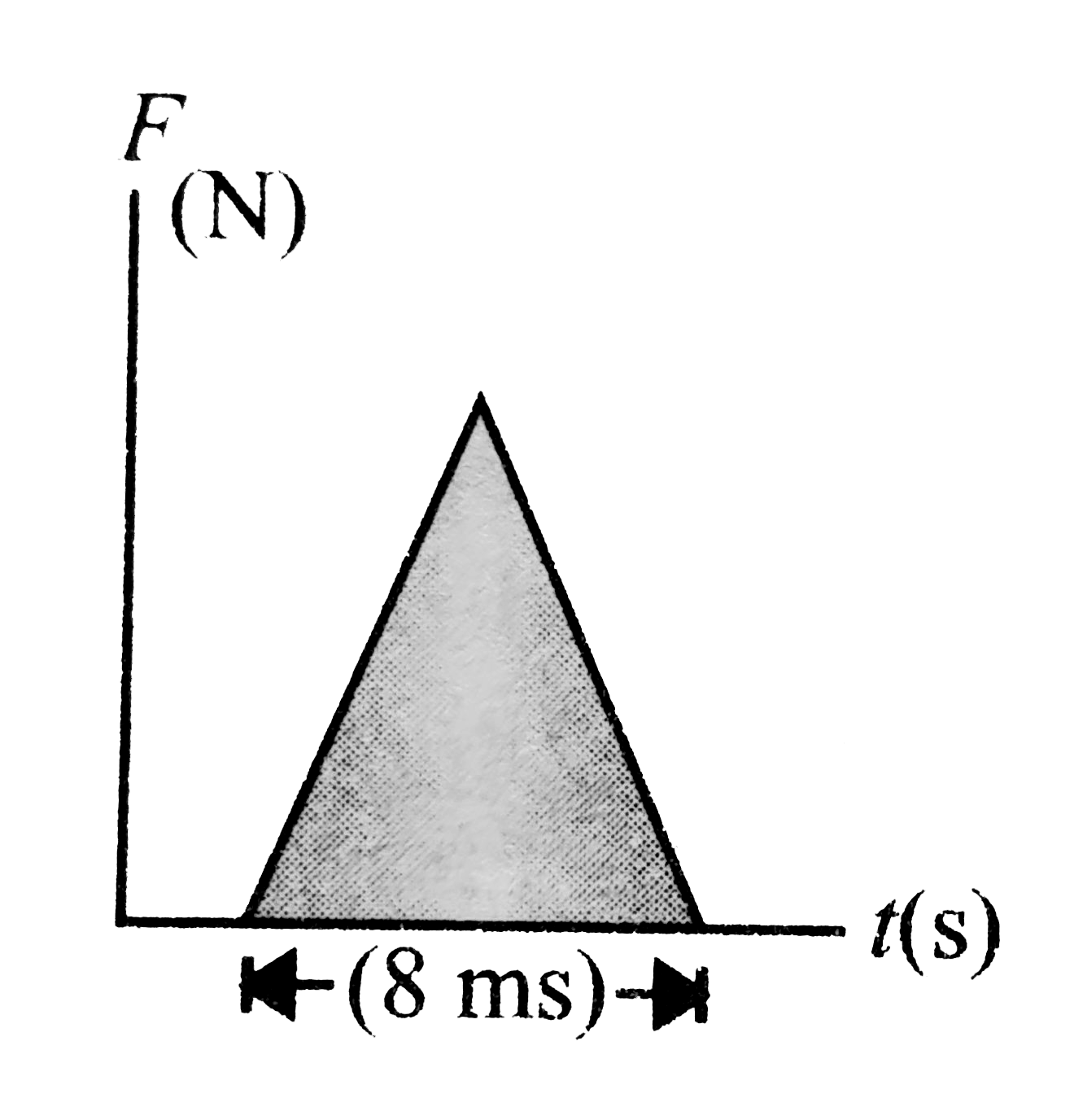 After collision with the hard floor, the ball will bounce to a height 05:47View Solution
After collision with the hard floor, the ball will bounce to a height 05:47View SolutionTwo persons, A of mass `60 kg` and `B` of mass `40 kg`, are standing on a horizontal platform of mass `50 kg`. The platform is supported on wheels on a horizontal frictionless surface and is initially at rest. Consider the following situations.

(i) Both `A` and `B` jump from the platform simultaneously and in the same horizontal direction.
(ii) A jumps first in a horizontal direction and after a few seconds `B` also jumps in the same direction. In both the situations above, just after the jump, the person (`A` or `B`) moves away from the platform with a speed of `3 m//s` relative to the platform and along the horizontal.
In situation (i), just after both `A` and `B` jump from the platform, velocity of centre of mass of the system (`A, B` and the platform) is05:22View SolutionTwo persons, A of mass `60 kg` and `B` of mass `40 kg`, are standing on a horizontal platform of mass `50 kg`. The platform is supported on wheels on a horizontal frictionless surface and is initially at rest. Consider the following situations.

(i) Both `A` and `B` jump from the platform simultaneously and in the same horizontal direction.
(ii) A jumps first in a horizontal direction and after a few seconds `B` also jumps in the same direction. In both the situations above, just after the jump, the person (`A` or `B`) moves away from the platform with a speed of `3 m//s` relative to the platform and along the horizontal.
Final speed of the platform in situation (i), i.e., just after both `A` and `B` have jumped will be a.05:22View SolutionTwo persons, A of mass `60 kg` and `B` of mass `40 kg`, are standing on a horizontal platform of mass `50 kg`. The platform is supported on wheels on a horizontal frictionless surface and is initially at rest. Consider the following situations.

(i) Both `A` and `B` jump from the platform simultaneously and in the same horizontal direction.
(ii) A jumps first in a horizontal direction and after a few seconds `B` also jumps in the same direction. In both the situations above, just after the jump, the person (`A` or `B`) moves away from the platform with a speed of `3 m//s` relative to the platform and along the horizontal.
Final speed of the platform in situation (ii), i.e., just after `B` has jumped, will be nearly05:22View SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of `2 m` from the wall, has a point mass `M` of `2 kg` attached to it at a distance of `1 m` from the wall. A mass in of `0.5 kg` is attached to the free end. The system is initially held at rest so that the string is horizontal between wall and pulley and vertical beyond the pulley as shown in Fig. The system is released from the rest from the position as shown.
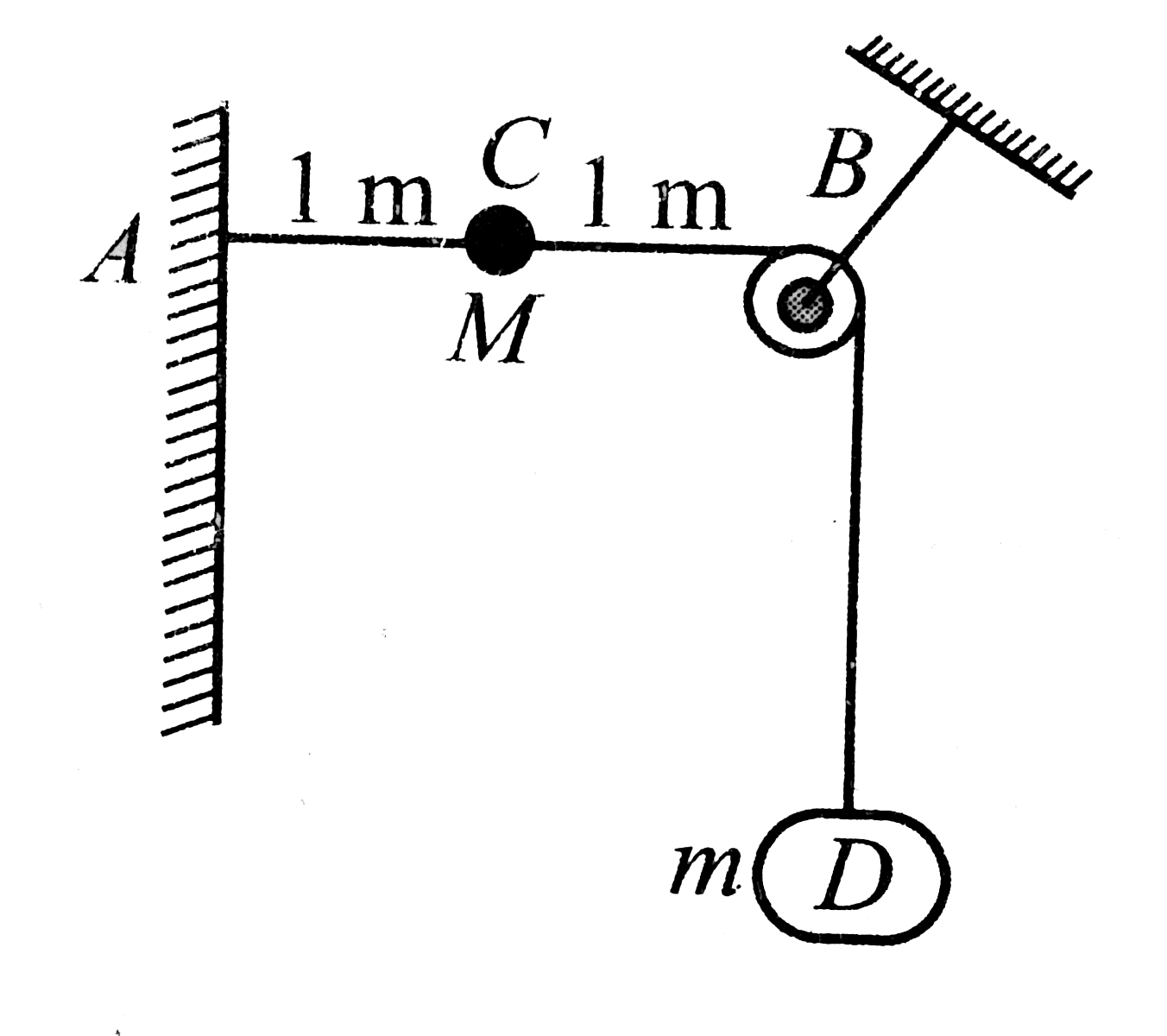
The ratio of velocity of `M` and `m` when `M` strikes the wall isView SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of `2m` from the wall, has a point mass M of `2kg` attached to it at a distance of `1m` from the wall. A mass `m` of `0.5kg` is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? `(g=10ms^-2)`04:40View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation `alpha=45^(@)` and `beta=tan^(-1)3` towards top of a cliff, `20 m` away from the point of firing. If both the shells reach the top simultaneously, then
muzzle velocity is06:08View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation `alpha=45^(@)` and `beta=tan^(-1)3` towards top of a cliff, `20 m` away from the point of firing. If both the shells reach the top simultaneously, then
height of the cliff is06:08View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation `alpha=45^(@)` and `beta=tan^(-1)3` towards top of a cliff, `20 m` away from the point of firing. If both the shells reach the top simultaneously, then
time interval between two frings is06:08View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation `alpha=45^(@)` and `beta=tan^(-1)3` towards top of a cliff, `20 m` away from the point of firing. If both the shells reach the top simultaneously, then
If just before striking the top of cliff, the two shells get stuck together, considering elastic collision of combined body with the top of cliff, then maximum height reached by the combined body is06:08View SolutionA ball of mass `m` is thrown at an angle of `45^(@)` to the horizontal,, from the top of a `65 m` high tower `AB` as shown in Fig. at `t = 0`. Another identical ball is thrown with velocity `20 m//s` horizontally towards `AB` from the top of a `30 m` high tower `CD 1 s` after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the two balls will collide at time `t =`05:11View SolutionA ball of mass `m` is thrown at an angle of `45^(@)` to the horizontal,, from the top of a `65 m` high tower `AB` as shown in Fig. at `t = 0`. Another identical ball is thrown with velocity `20 m//s` horizontally towards `AB` from the top of a `30 m` high tower `CD 1 s` after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the height from the ground where the two balls will collide is05:11View SolutionA ball of mass `m` is thrown at an angle of `45^(@)` to the horizontal,, from the top of a `65 m` high tower `AB` as shown in Fig. at `t = 0`. Another identical ball is thrown with velocity `20 m//s` horizontally towards `AB` from the top of a `30 m` high tower `CD 1 s` after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the distance `AC` is05:11View SolutionA ball of mass `m` is thrown at an angle of `45^(@)` to the horizontal,, from the top of a `65 m` high tower `AB` as shown in Fig. at `t = 0`. Another identical ball is thrown with velocity `20 m//s` horizontally towards `AB` from the top of a `30 m` high tower `CD 1 s` after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

. the velocity of combined ball just after they struck together is05:11View SolutionA ball A of mass `m` is suspended by a thread of length `r = 1.2 m`. Another ball `B` of mass `2m` is projected from the ground with velocity it `u= 9 m//s` such that at the highest point of its trajectory it collides head-on elastically with ball `A`. It is observed that during subsequent motion, tension in the thread at the highest point is equal to `mg`.
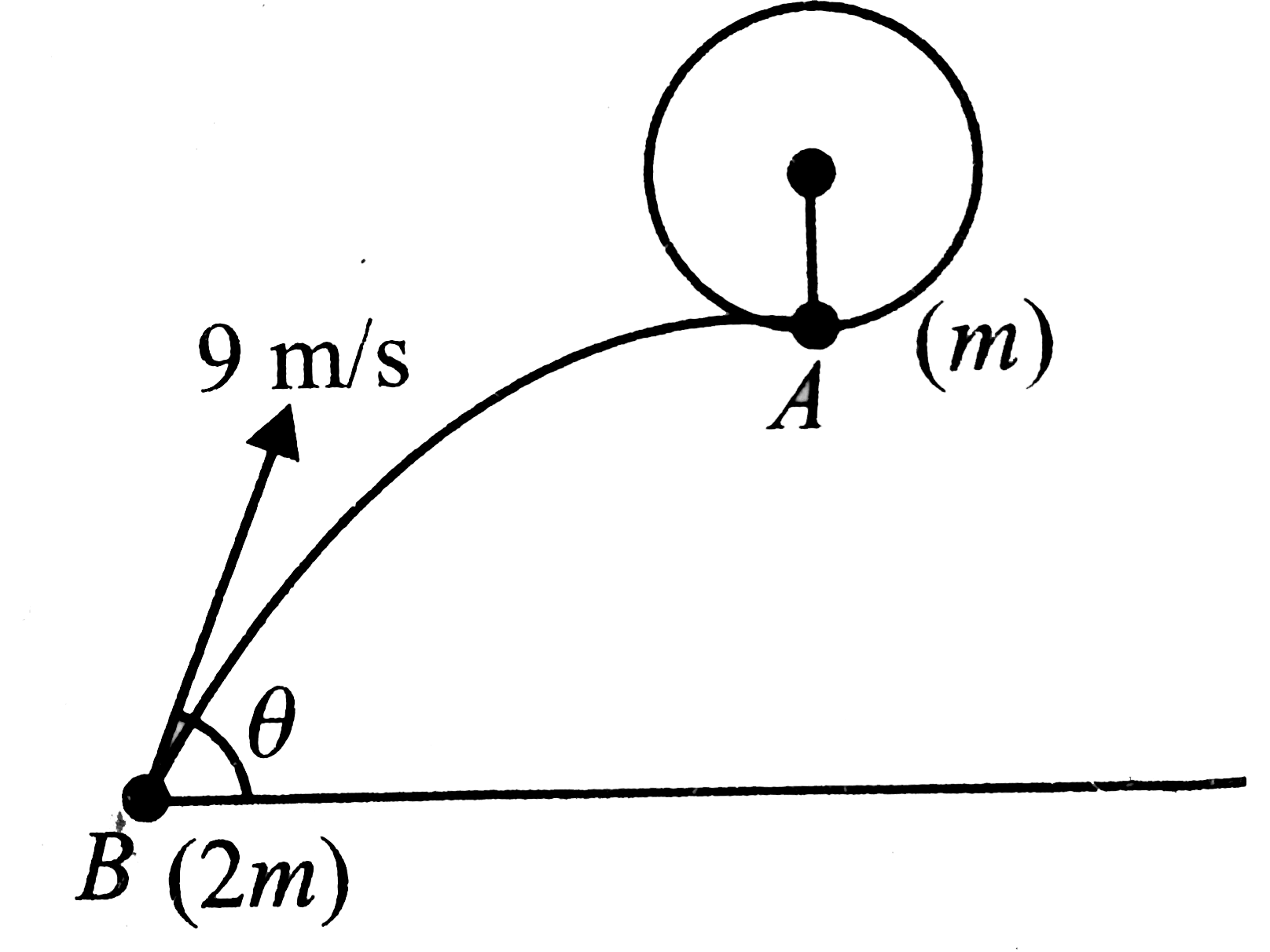 ltrgt At highest point of `B`, the velocity of ball `A` is View Solution
ltrgt At highest point of `B`, the velocity of ball `A` is View SolutionA ball A of mass `m` is suspended by a thread of length `r = 1.2 m`. Another ball `B` of mass `2m` is projected from the ground with velocity it `u= 9 m//s` such that at the highest point of its trajectory it collides head-on elastically with ball `A`. It is observed that during subsequent motion, tension in the thread at the highest point is equal to `mg`.

The angle of projection (`theta`) of ball `B` isView SolutionA ball A of mass `m` is suspended by a thread of length `r = 1.2 m`. Another ball `B` of mass `2m` is projected from the ground with velocity it `u= 9 m//s` such that at the highest point of its trajectory it collides head-on elastically with ball `A`. It is observed that during subsequent motion, tension in the thread at the highest point is equal to `mg`.

The height of the point of suspension of ball `A` from the ground isView SolutionTwo identical buggies of each of mass `150 kg` move one after the other friction with same velocity `4m/s`. A man of mass `m` rides the rear buggy. At a certain moment, the man jumps into the front buggy with a velocity v relative to his buggy. As a result of this process, real boggy stops. If the sum of kinetic energies of the man and the front buggy just after collision with the from buggy differs from that just before collision by `2700 J` then
the mass `m` of the man is03:34View SolutionTwo identical buggies of each of mass `150 kg` move one after the other friction with same velocity `4m//s`. A man of mass `m` rides the rear buggy. At a certain moment, the man jumps into the front buggy with a velocity v relative to his buggy. As a result of this process, real boggy stops. If the sum of kinetic energies of the man and the front buggy just after collision with the from buggy differs from that just before collision by `2700 J` then
The velocity `v` of the man relartive to the buggy is03:34View SolutionIn the arrangement shown in Fig. the ball and the block have the same mass `m=1 kg` each, `theta=60^(@)` and length `l = 2.50m`. Coefficient of friction between the block and the floor is `0.5`. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance `2.50 m`.

The velocity of block just after collision is04:50View SolutionIn the arrangement shown in Fig. the ball and the block have the same mass `m=1 kg` each, `theta=60^(@)` and length `l = 2.50m`. Coefficient of friction between the block and the floor is `0.5`. When the ball is released from the position shown in Fig. it collides with the block and the block stops after moving a distance `2.50 m`.
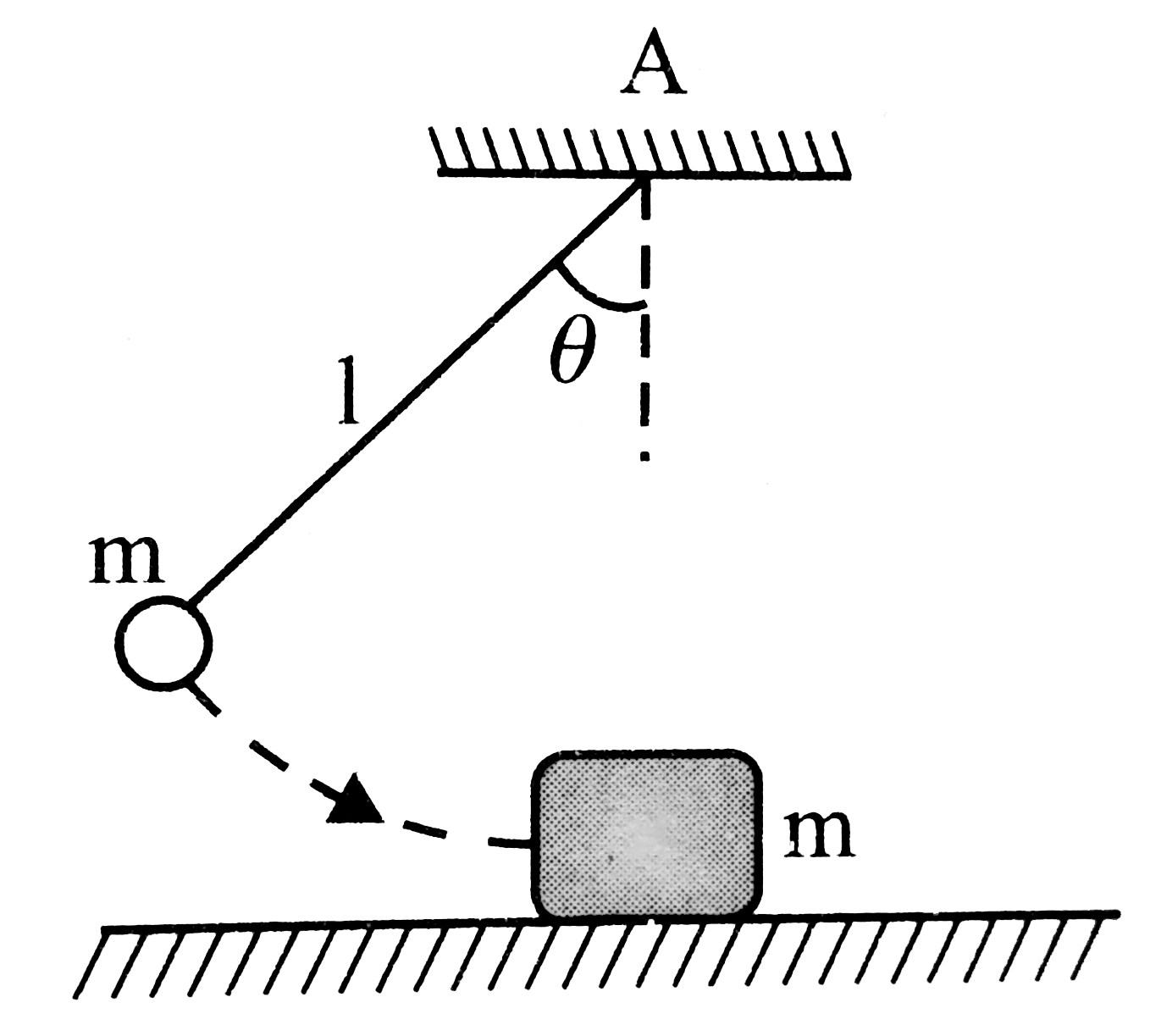
The coefficient of restitution for collision between the ball and the block is04:50View SolutionA ball of mass in `m= 1 kg` is hung vertically by a thread of length `l = 1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M= 4 kg`. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass `m=1` kg, moving horizontally with velocity `v_(0) = 6 m//s` collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
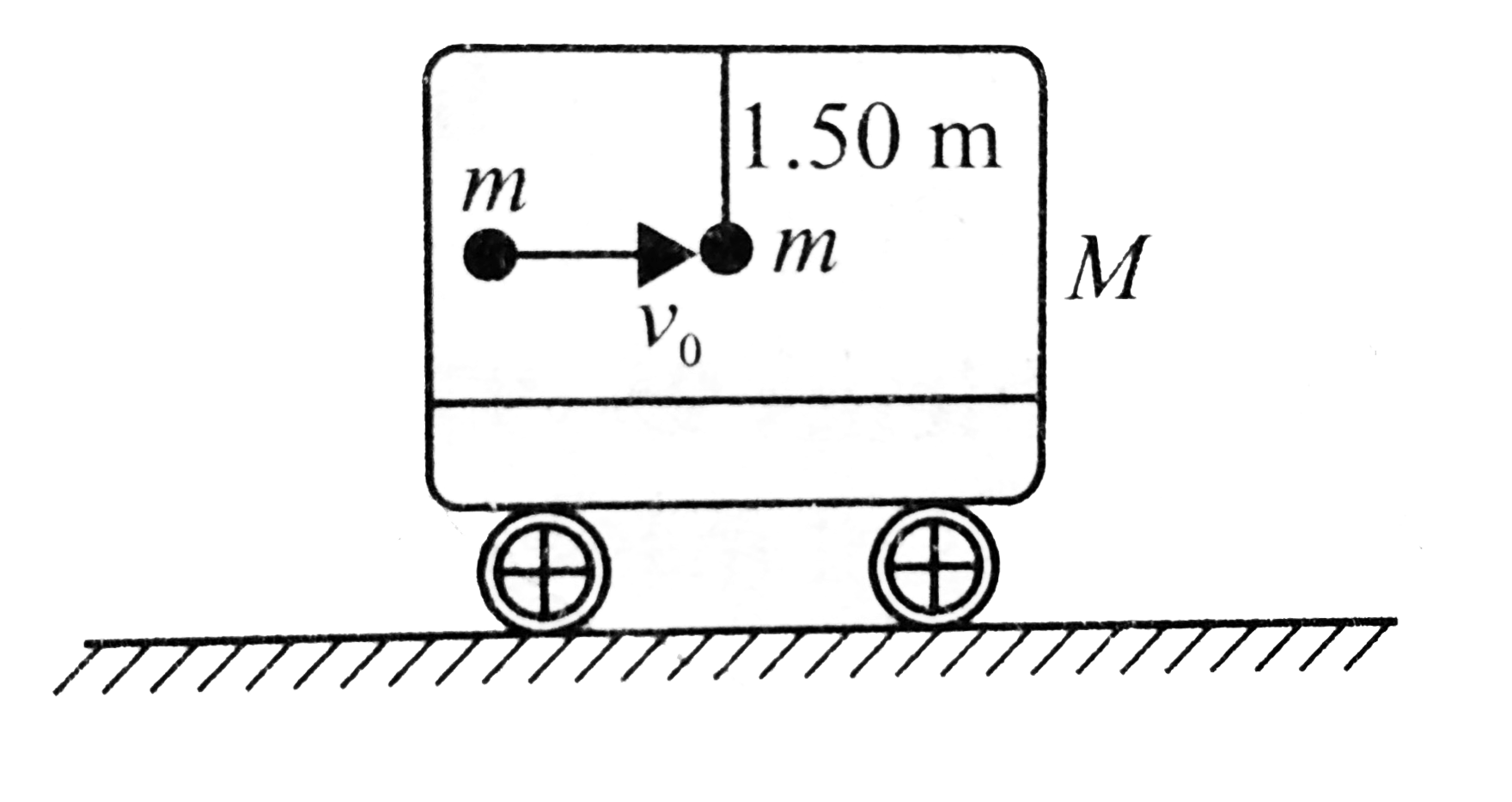
The velocity of the combined body just after collision is04:43View SolutionA ball of mass in `m= 1 kg` is hung vertically by a thread of length `l = 1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M= 4 kg`. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass `m=1 kg`, moving horizontally with velocity `v_(0 )= 6 m//s` collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.

At the time of maximum deflection of the thread with vertical, the trolley will move with velocity04:43View SolutionA ball of mass in `m= 1 kg` is hung vertically by a thread of length `l = 1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M= 4 kg`. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass `m=1 kg`, moving horizontally with velocity `v_(0) = 6 m//s` collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
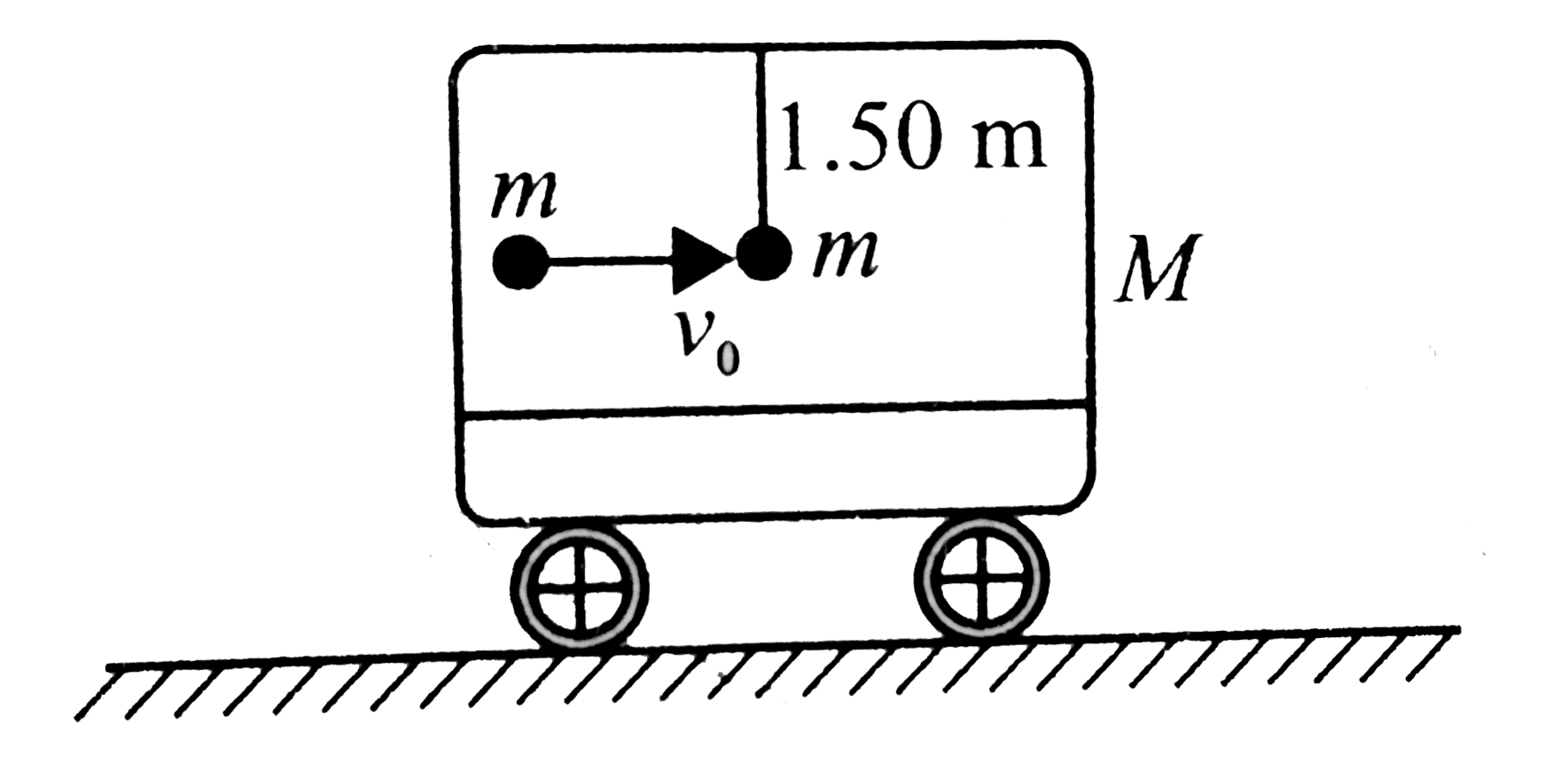
The maximum deflection of the thread with the vertical is04:43View SolutionTwo balls of masses `m_(1)=100 g` and `m_(2)=300 g` are suspended from point `A` by two equal inextensible threads, each of length `l=32/35m`. Ball of mass `m_(1)` is drawn aside and held at the same level as `A` but at a distance `(sqrt(3)/2)l` from `A`, as shown in Fig. When ball `m_(1)` is released, it collides elastically with the stationary ball of mass `m_(2)`.
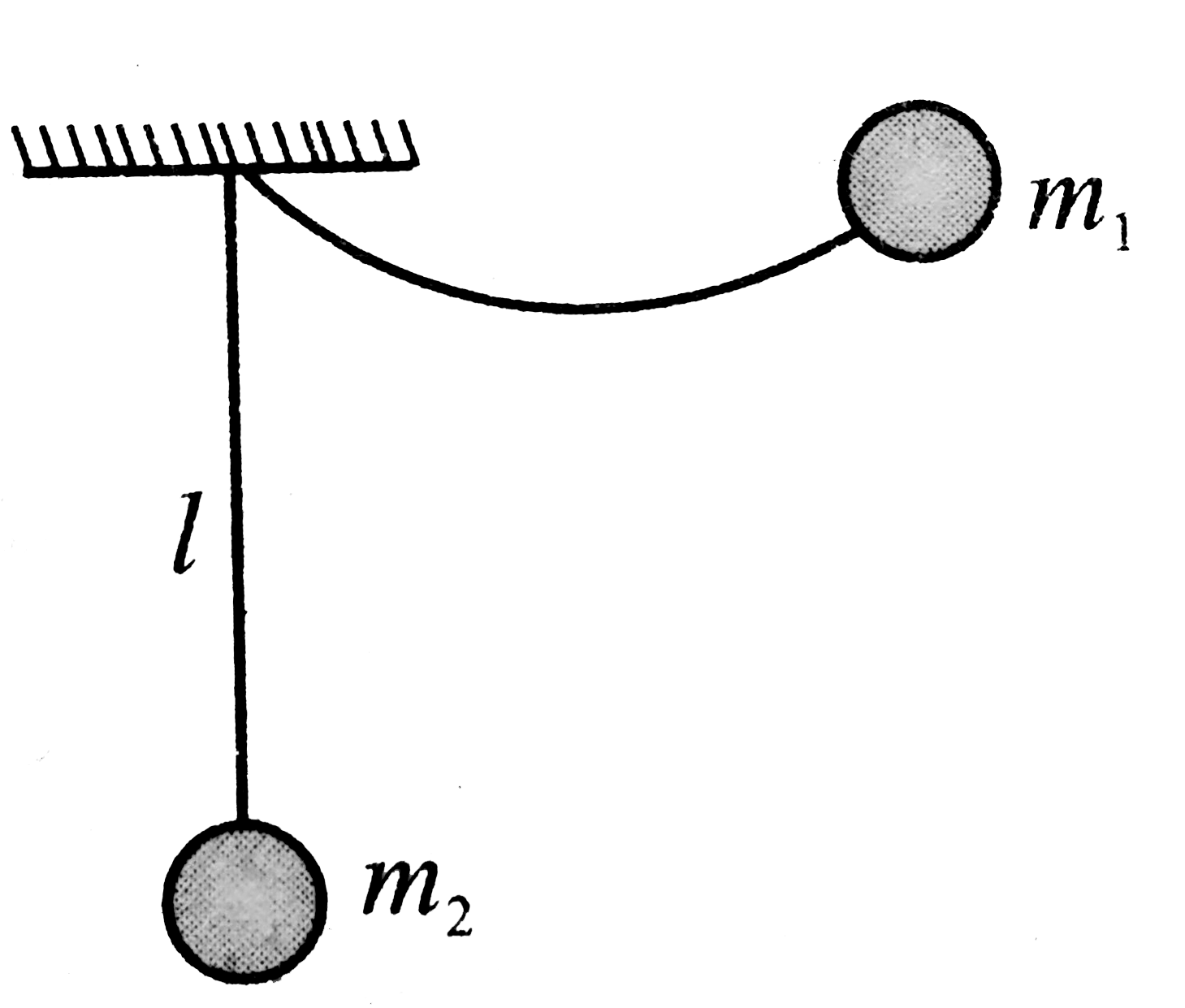
Velocity `u_(1)` with which the hall of mass `m_(1)` collides with the other ball isView SolutionTwo balls of masses `m_(1)=100 g` and `m_(2)=300 g` are suspended from point `A` by two equal inextensible threads, each of length `l=32/35m`. Ball of mass `m_(1)` is drawn aside and held at the same level as `A` but at a distance `(sqrt(3)/2)l` from `A`, as shown in Fig. When ball `m_(1)` is released, it collides elastically with the stationary ball of mass `m_(2)`.
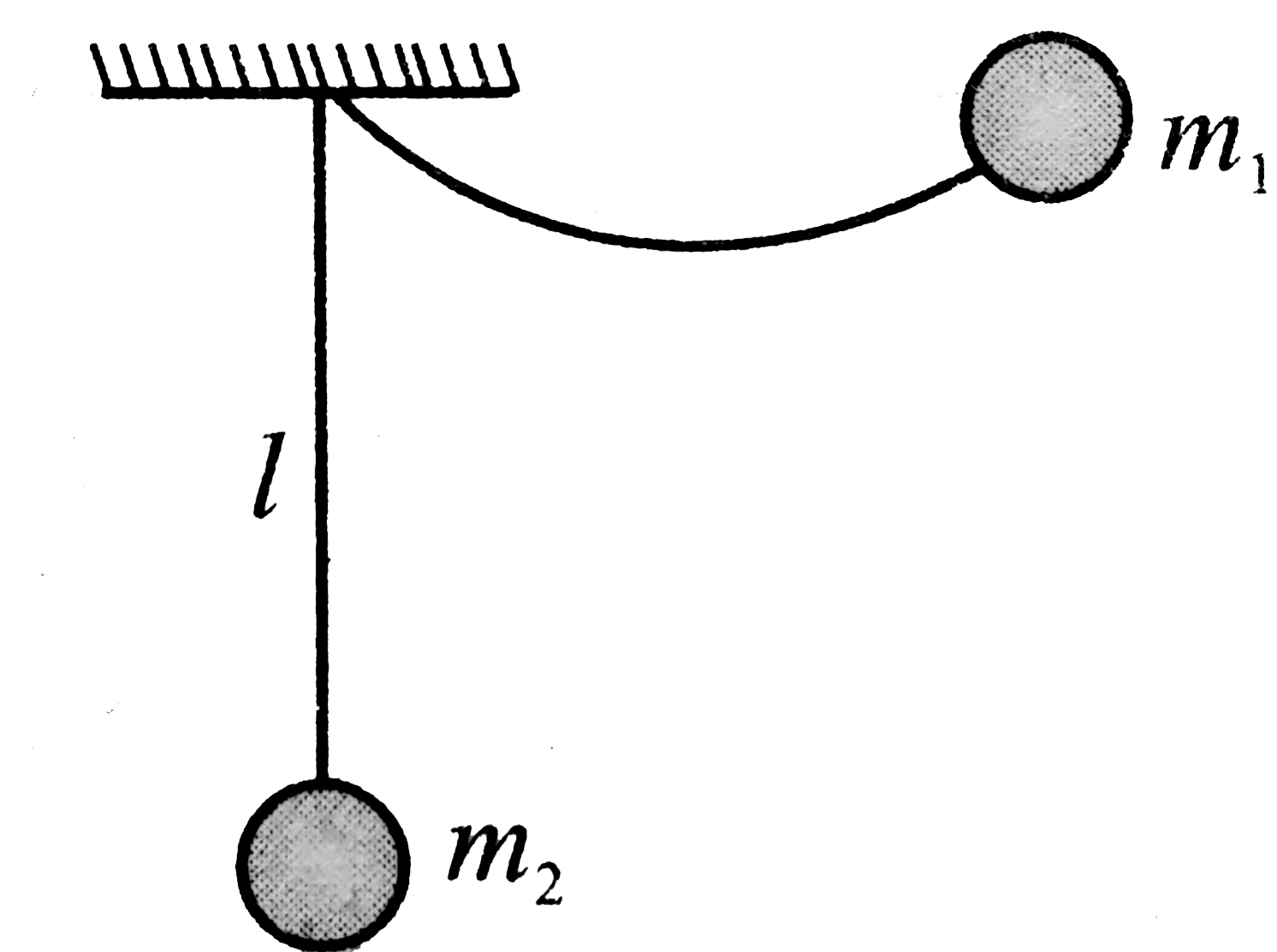 The maximum rise of centre of mass of the ball of mass`m_(2)` isView Solution
The maximum rise of centre of mass of the ball of mass`m_(2)` isView SolutionTwo identical blocks `A` and `B` each of mass `2 kg` are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell `C` of mass `1 kg` moving vertically upwards with velocity `9 m//s` collides with block `B` and gets stuck to it.

Calculate the time after which block `B` starts moving downwards.06:39View SolutionTwo identical blocks `A` and `B` each of mass `2 kg` are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell `C` of mass `1 kg` moving vertically upwards with velocity `9 m//s` collides with block `B` and gets stuck to it.

The maximum height reached by `B`10:59View SolutionTwo identical blocks `A` and `B` each of mass `2 kg` are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell `C` of mass `1 kg` moving vertically upwards with velocity `9 m//s` collides with block `B` and gets stuck to it.

The loss of mechanical energy up to that instant is06:39View SolutionA pan of mass `m = 1.5 kg` and a block of mass `M = 3 kg` are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass `m_0 = 0.5 kg` collides with the pan at a speed `v_0= 20 m//s`. Consider this instant of collision as `t = 0`. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Mark the correct statement(s) for this situation07:42View SolutionA pan of mass `m = 1.5 kg` and a block of mass `M = 3 kg` are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass `m_0 = 0.5 kg` collides with the pan at a speed `v_0= 20 m//s`. Consider this instant of collision as `t = 0`. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the time t at which the block strikes the floor for the first time07:42View SolutionA pan of mass `m = 1.5 kg` and a block of mass `M = 3 kg` are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass `m_0 = 0.5 kg` collides with the pan at a speed `v_0= 20 m//s`. Consider this instant of collision as `t = 0`. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the velocity of pan + ball system at `t = 2.6 s`. Assume that the block comes to rest instantaneously after striking the floor.07:42View SolutionA pan of mass `m = 1.5 kg` and a block of mass `M = 3 kg` are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass `m_0 = 0.5 kg` collides with the pan at a speed `v_0= 20 m//s`. Consider this instant of collision as `t = 0`. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

. Find the maximum height reached by the block alter the second jerk.07:42View SolutionA horizontal frictionless rod is threaded through a bead of mass `m`. The length of the cart is `L` and the radius of the bead, `r`, is very small in comparison with `L(r lt lt L)`. Initially at (`t = 0`) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity `v_(0)` towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
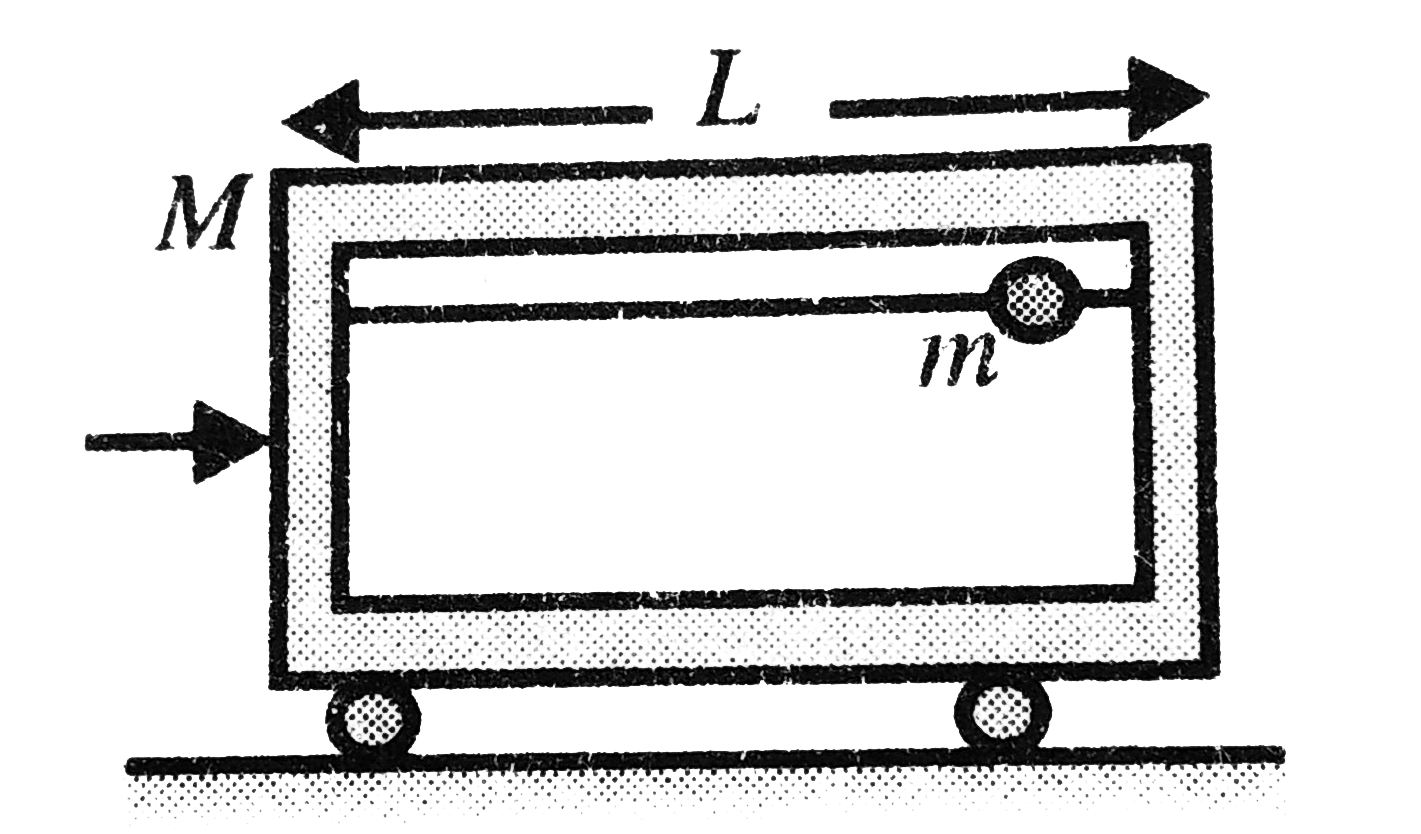
What is the velocity of the cart just after the first collision?03:00View SolutionA horizontal frictionless rod is threaded through a bead of mass `m`. The length of the cart is `L` and the radius of the bead, `r`, is very small in comparison with `L(r lt lt L)`. Initially at (`t = 0`) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity `v_(0)` towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
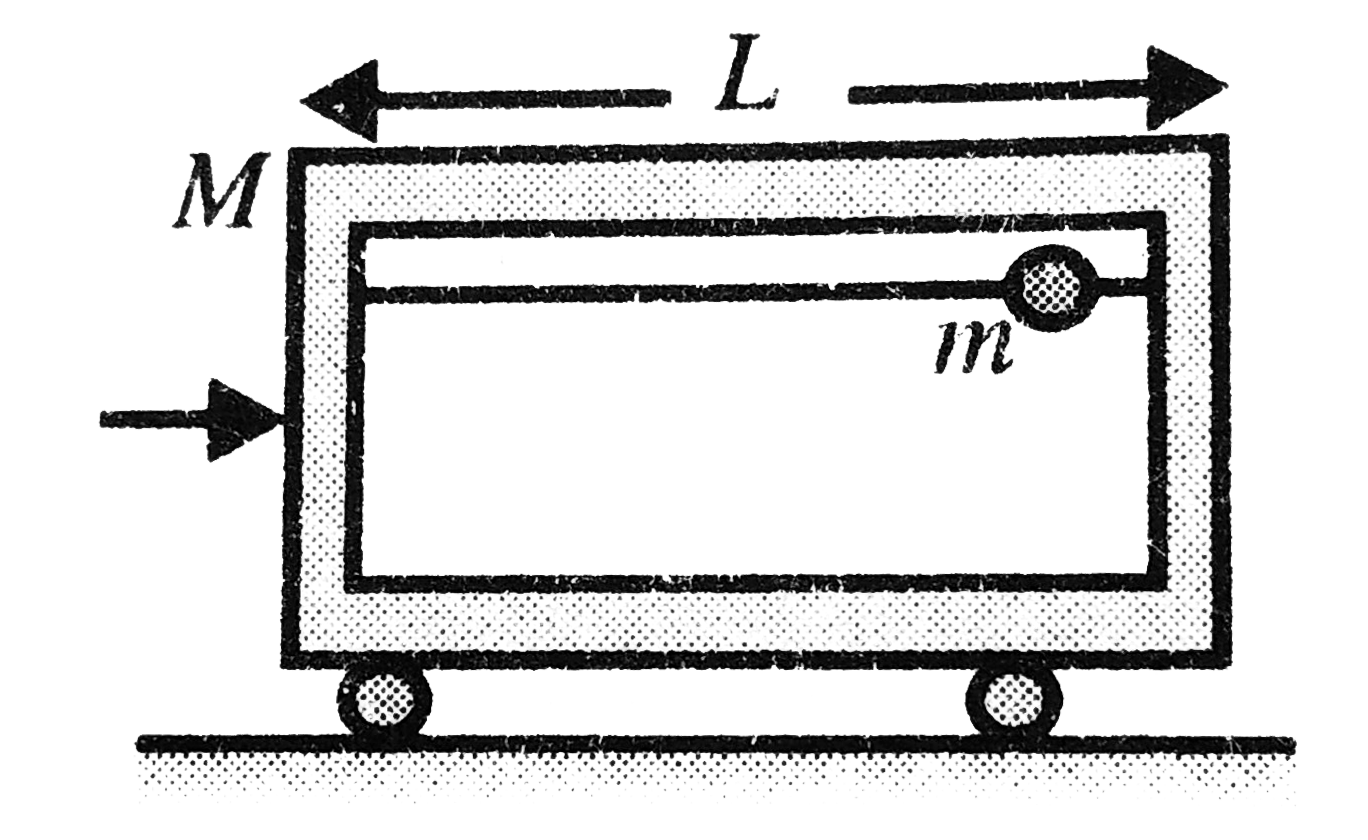
Velocity of bead just after the first collision is03:00View SolutionA horizontal frictionless rod is threaded through a bead of mass `m`. The length of the cart is `L` and the radius of the bead, `r`, is very small in comparison with `L(r lt lt L)`. Initially at (`t = 0`) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity `v_(0)` towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
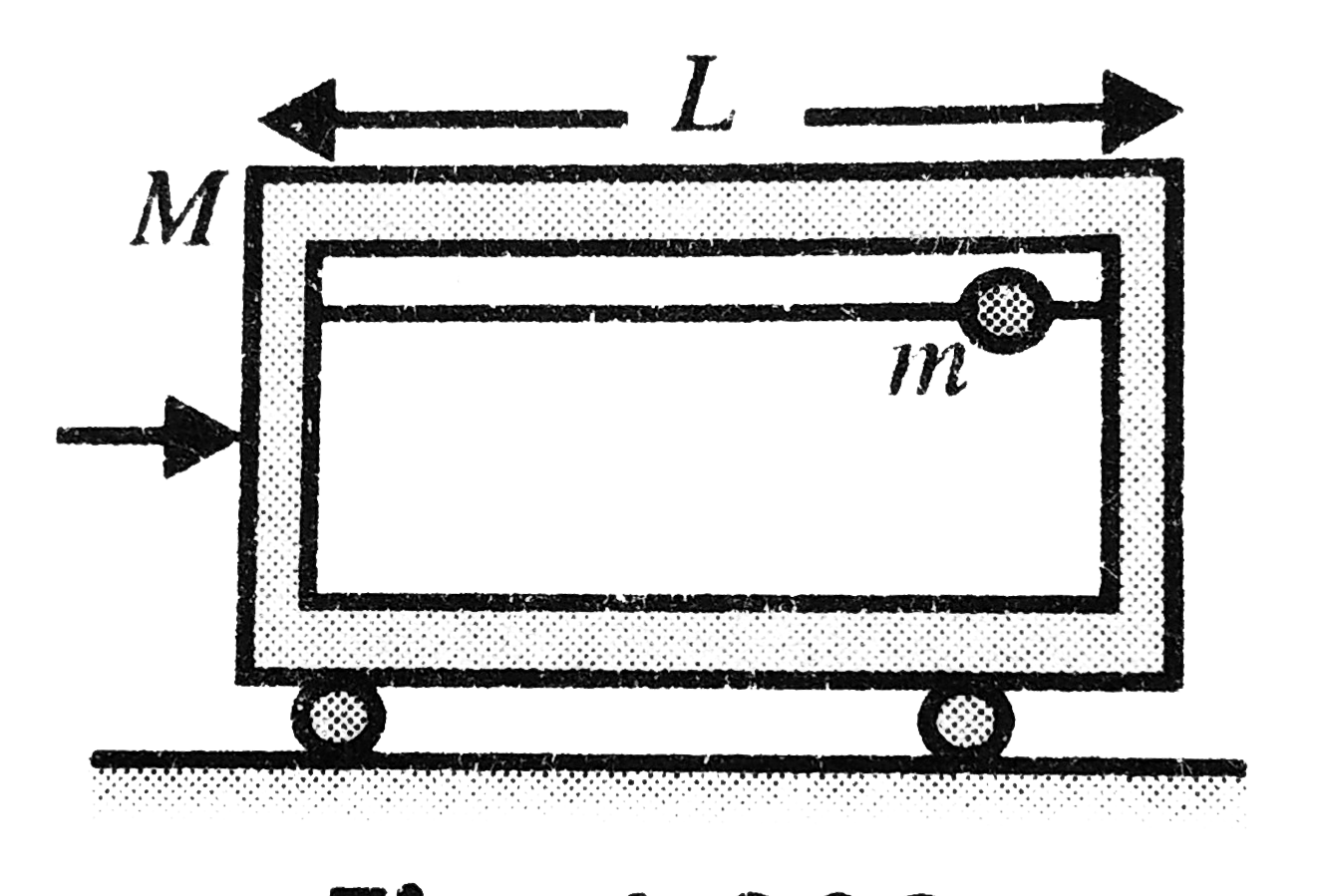
The first collision takes place at time ti and the second collision takes place at time `t_(2)`. Find `t_(2)-t_(1)`03:00View SolutionAn initially stationary box on a frictionless floor explodes into two pieces, piece `A` with mass `m_(A)` and piece `B` with mass `m_(B)`. Two pieces then move across the floor along `x`-axis. Graph of position versus time for the two pieces are given

Which graphs pertain to physically possible explosion?01:57View SolutionAn initially stationary box on a frictionless floor explodes into two pieces, piece `A` with mass `m_(A)` and piece `B` with mass `m_(B)`. Two pieces then move across the floor along `x`-axis. Graph of position versus time for the two pieces are given

If graphs are possible then. in which of the following case, external impulse must be acting on the box?01:57View SolutionA circular disc of mass `'2m'` and radius `'3r'` is resting on a flat frictionless surface. Another circular disc of mass m and radius `'2r'`, moving with a velocity `'u'`. hits the first disc as shown in the figure. The collision is elastic.
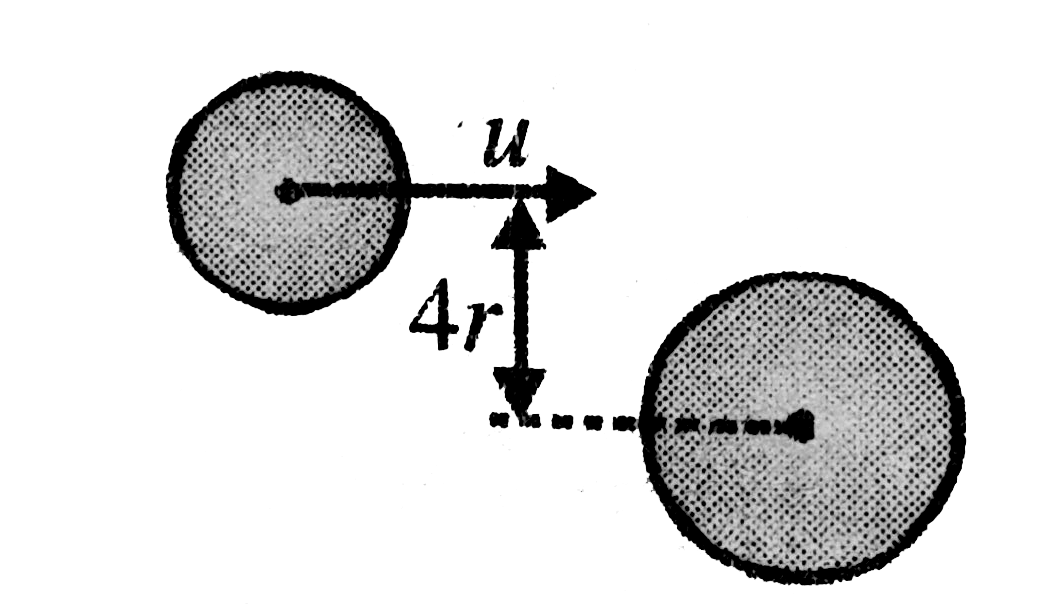
What is the tangential component of final velocity of the smaller disc?03:38View SolutionA circular disc of mass `'2m'` and radius `'3r'` is resting on a flat frictionless surface. Another circular disc of mass m and radius `'2r'`, moving with a velocity `'u'`. hits the first disc as shown in the figure. The collision is elastic.
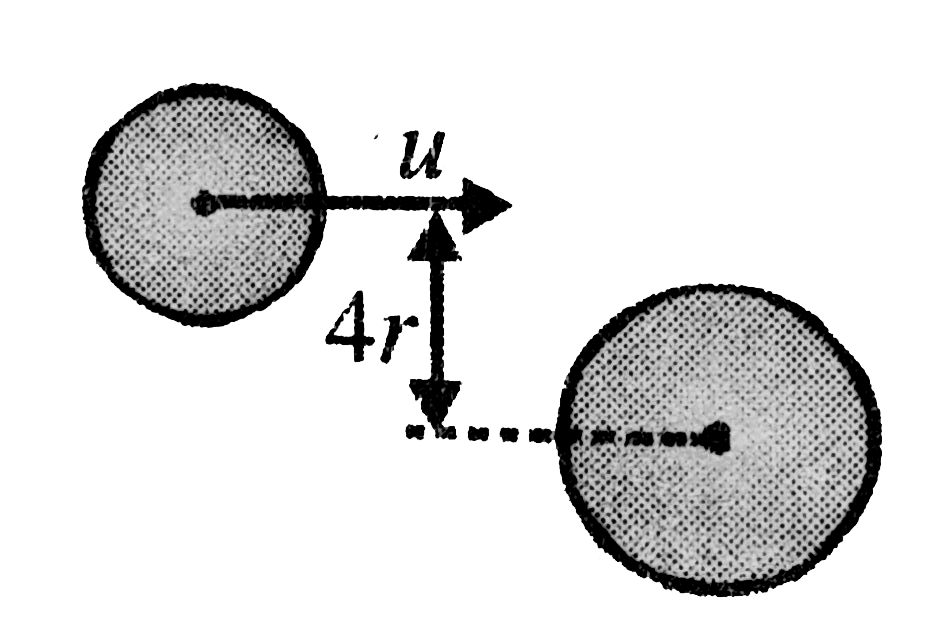
What is the magnitude of normal component of final velocity of the smaller disc'?03:38View SolutionA circular disc of mass `'2m'` and radius `'3r'` is resting on a flat frictionless surface. Another circular disc of mass m and radius `'2r'`, moving with a velocity `'u'`. hits the first disc as shown in the figure. The collision is elastic.
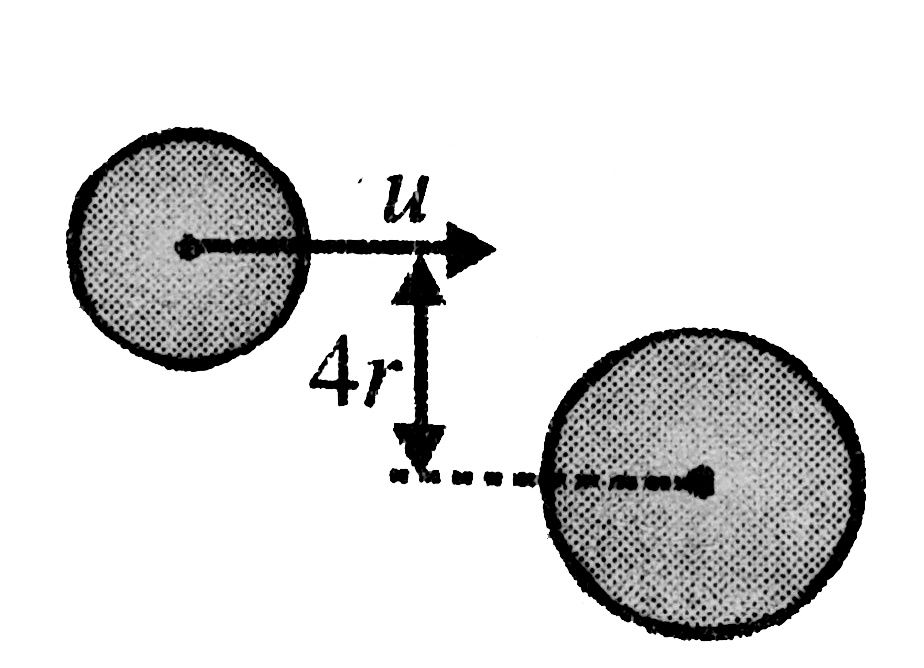 What is the final velocity of the heavier disc?03:38View Solution
What is the final velocity of the heavier disc?03:38View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected by an ideal sprit, of force constant `k`. The blocks are placed on smooth horizontal surface. A horizontal force `F` acts on the block `m_(1)`. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring02:20View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected by an ideal sprit, of force constant `k`. The blocks are placed on smooth horizontal surface. A horizontal force `F` acts on the block `m_(1)`. Initially spring is relaxed, both the blocks are at rest.
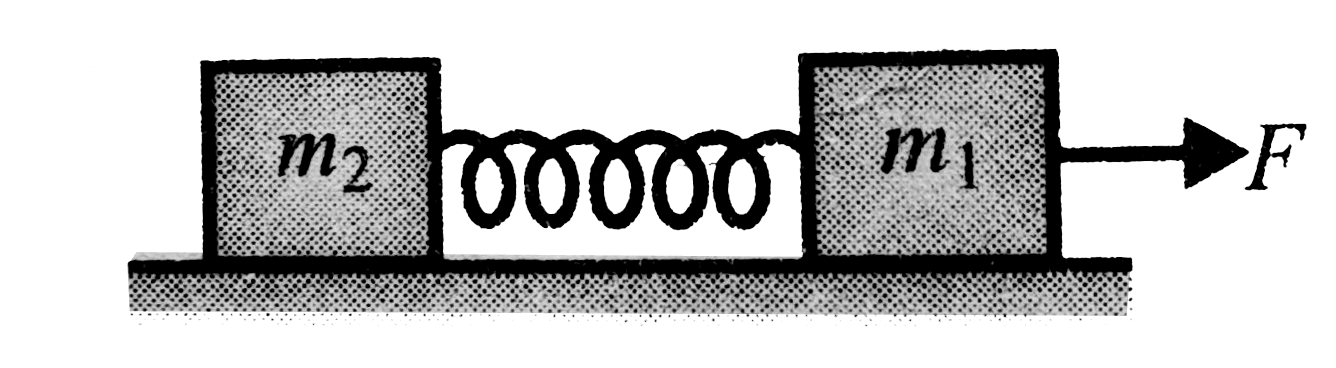
Which of the following statement is not true tn the watt of above system.02:20View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected by an ideal sprit, of force constant `k`. The blocks are placed on smooth horizontal surface. A horizontal force `F` acts on the block `m_(1)`. Initially spring is relaxed, both the blocks are at rest.
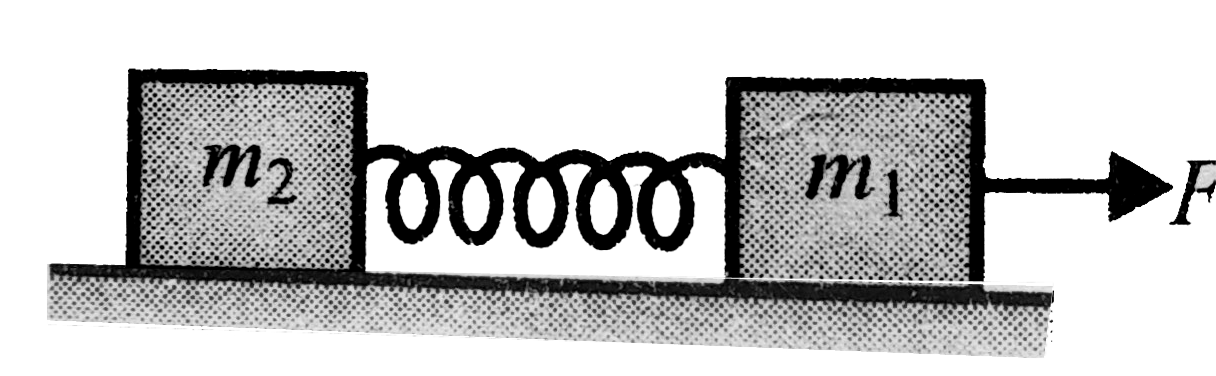
What is maximum elongation of spring.View SolutionA small ball `B` of mass `m` is suspended with light inelastic string of length `L` from a block `A` of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle `theta` from equilibrium position and then released.

The displacement of block when equilibrium position is06:04View SolutionA small ball `B` of mass `m` is suspended with light inelastic string of length `L` from a block `A` of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle `theta` from equilibrium position and then released.
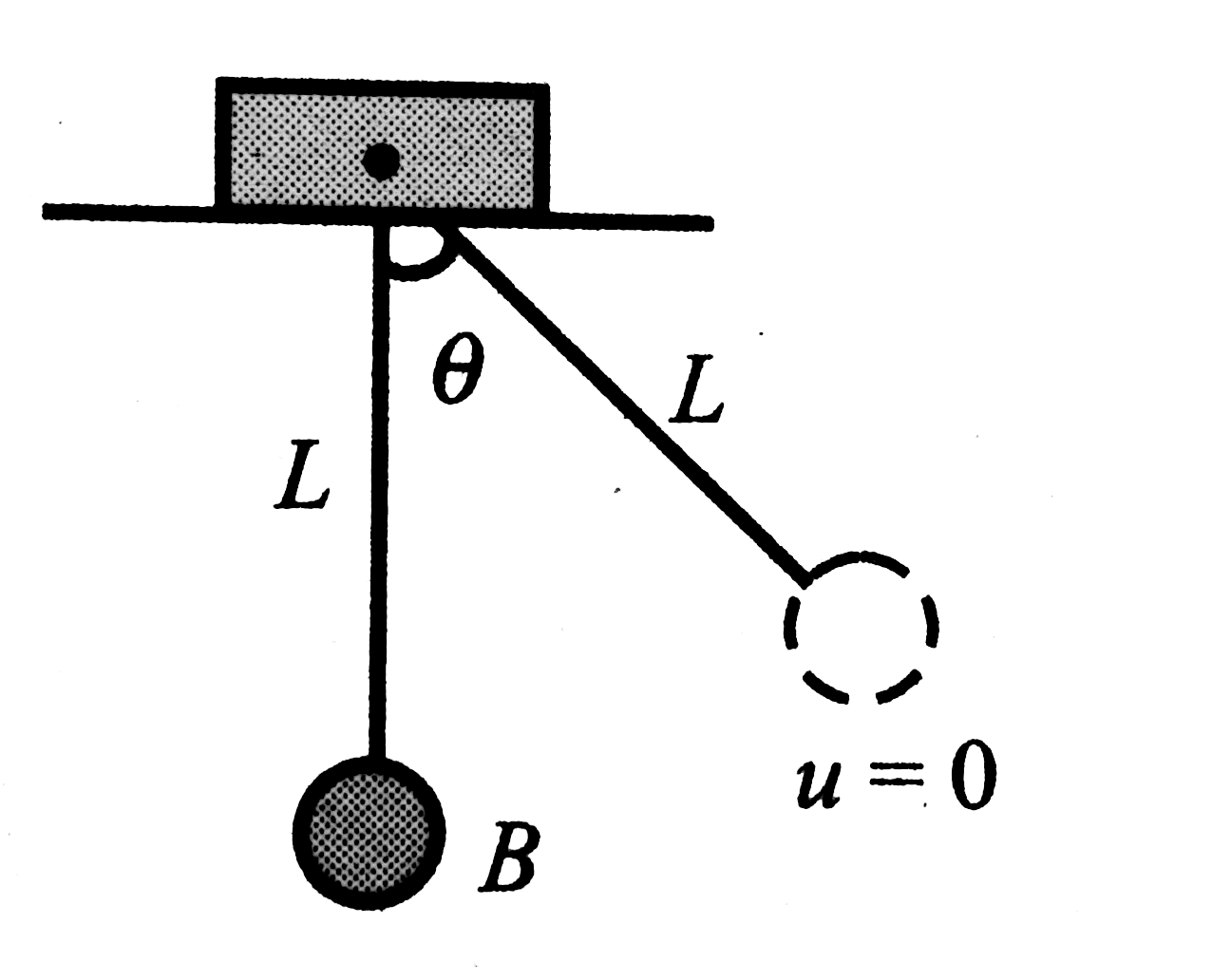
Tension in string when it is vertical, is06:04View SolutionA small ball `B` of mass `m` is suspended with light inelastic string of length `L` from a block `A` of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle `theta` from equilibrium position and then released.
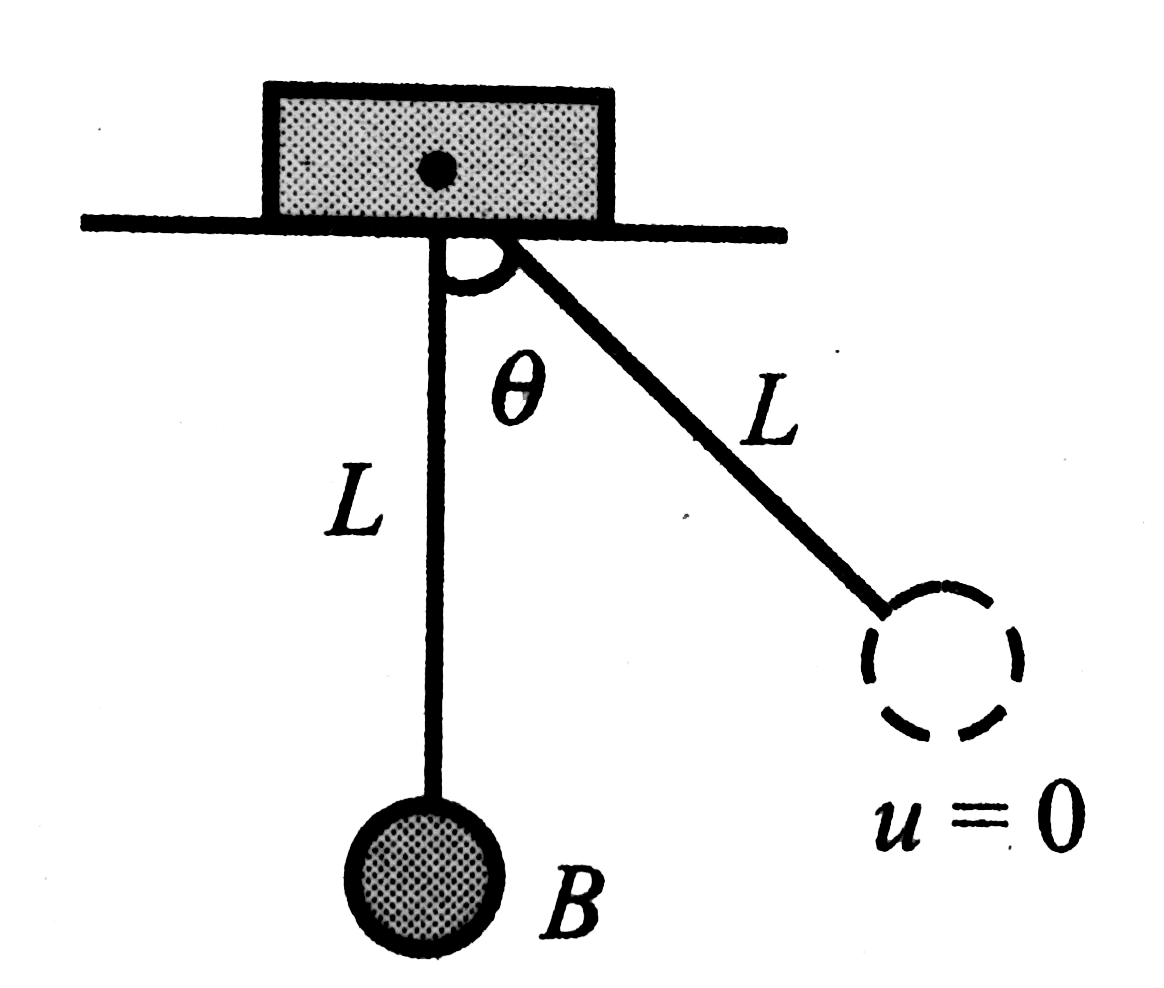
Maximum velocity of block during subsequent motion of the system after release of ball is06:04View SolutionA small ball `B` of mass `m` is suspended with light inelastic string of length `L` from a block `A` of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle `theta` from equilibrium position and then released.
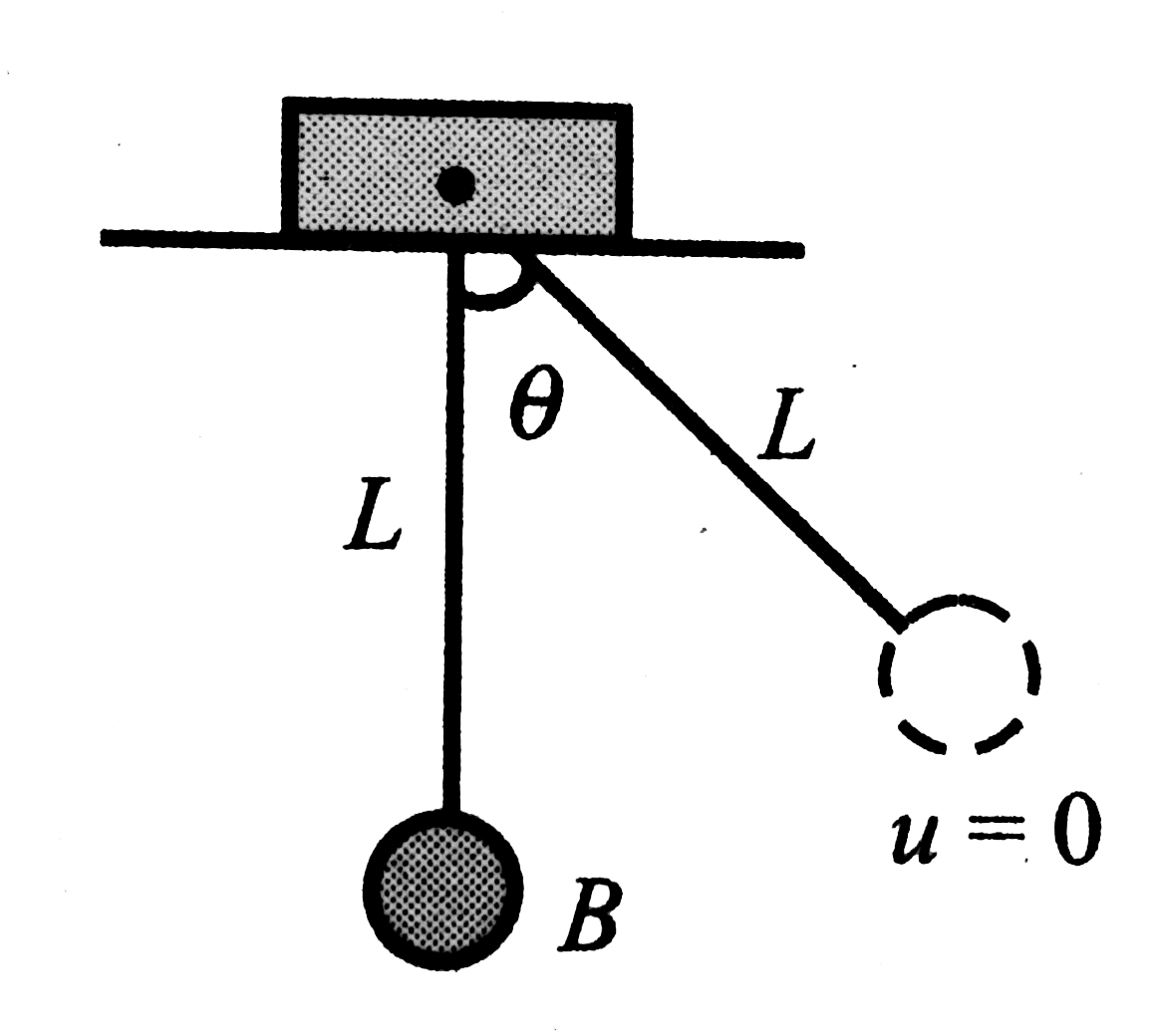 The displacement of centre of mass of `A + B` system till the string becomes vertical is 06:04View Solution
The displacement of centre of mass of `A + B` system till the string becomes vertical is 06:04View SolutionA small ball of mass `1 kg` is kept in circular path of radius `1 m` Inside a concentric smooth horizontal fixed casing of radius `R`. Angular speed of the ball in the circular motion is `1 rads^(-1)`. At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Total impulse imparted to the casing by the ball in first six collisions will be05:47View Solution
Linked Comprehension questions and complete solutions for chapter CENTRE OF MASS of CENGAGE PHYSICS (HINGLISH) of Class 11
