Complete Solutions to Exercise 3.2 of chapter RIGID BODY DYNAMICS 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Exercise 3.2 |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A circular disc of mass `M_(1)` and radius `R`, initially moving, With a constant angular speed `omega` is gently placed coaxially on a stationary circular disc of mass ` M_(2)` and radius `R`, as shown in Fig. There is a frictional force between the two discs.
If disc `M_(2)` is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. `/_\K//K_(i)`
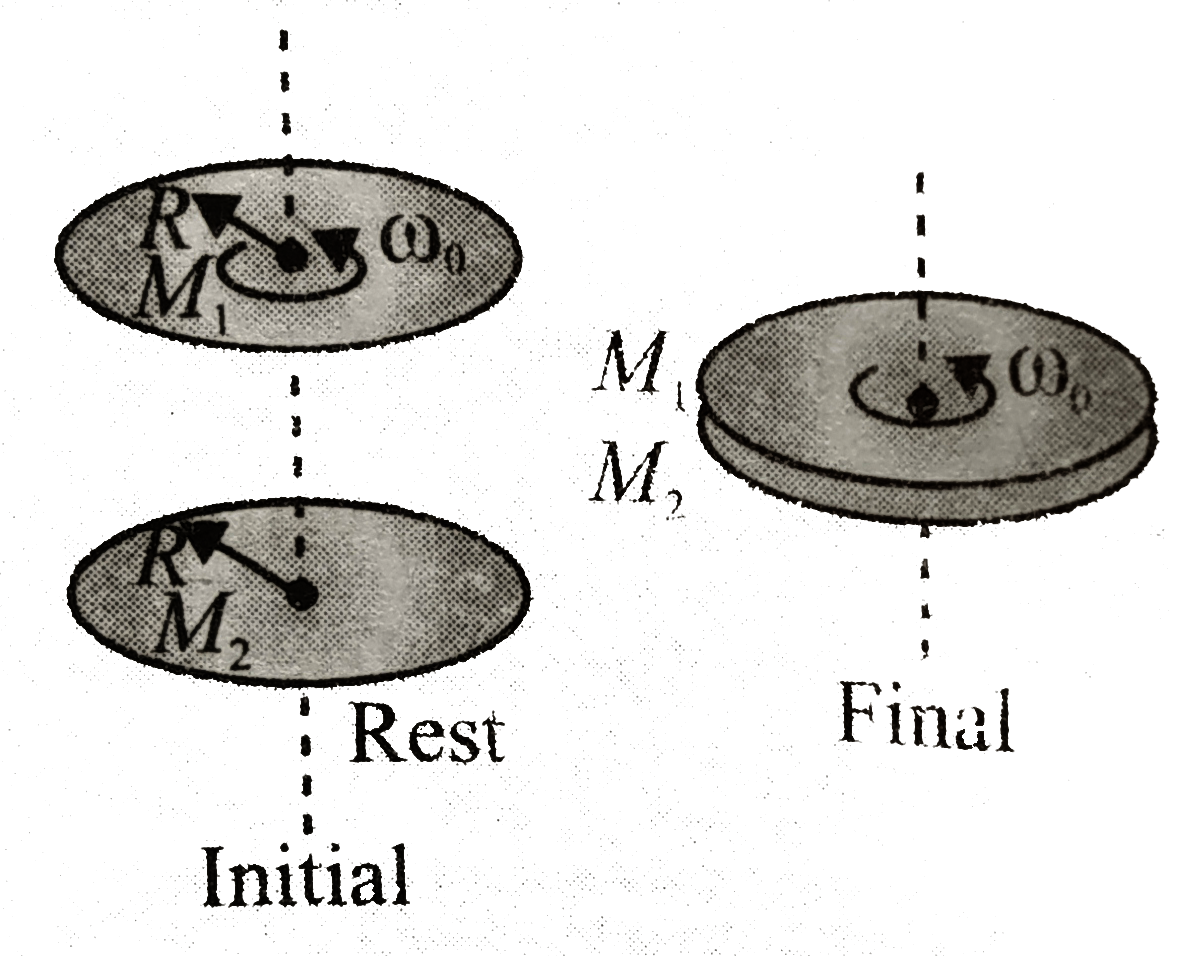
View SolutionA child of mass `m` is standing, on the periphery of a circular platform of radius `R`, which can rotate about its central axis. The moment of inertia of the platform is `I`. Child jumps off from the platform with a velocity `u` tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View SolutionSuppose in the previous poroblem, the child stays at rest on the platform and one of hils firend throws a ball of mas `m_(1)` towards thim with a velocity of `v` from a direction tangential to the platform and the child on the platform catches the ball. Find the angular velocity of the platform after he catches the ball.
View SolutionConsider a cylinder rolling on a horizontal plane. Its linear velocity is `v` and rotational angular velocity is `omega`. Find its angular momentum about point `P` on the ground as shown in Fig. What happens to this angular momentum if the cylinder is rotating in opposite direction but moving translationally in the same direction.

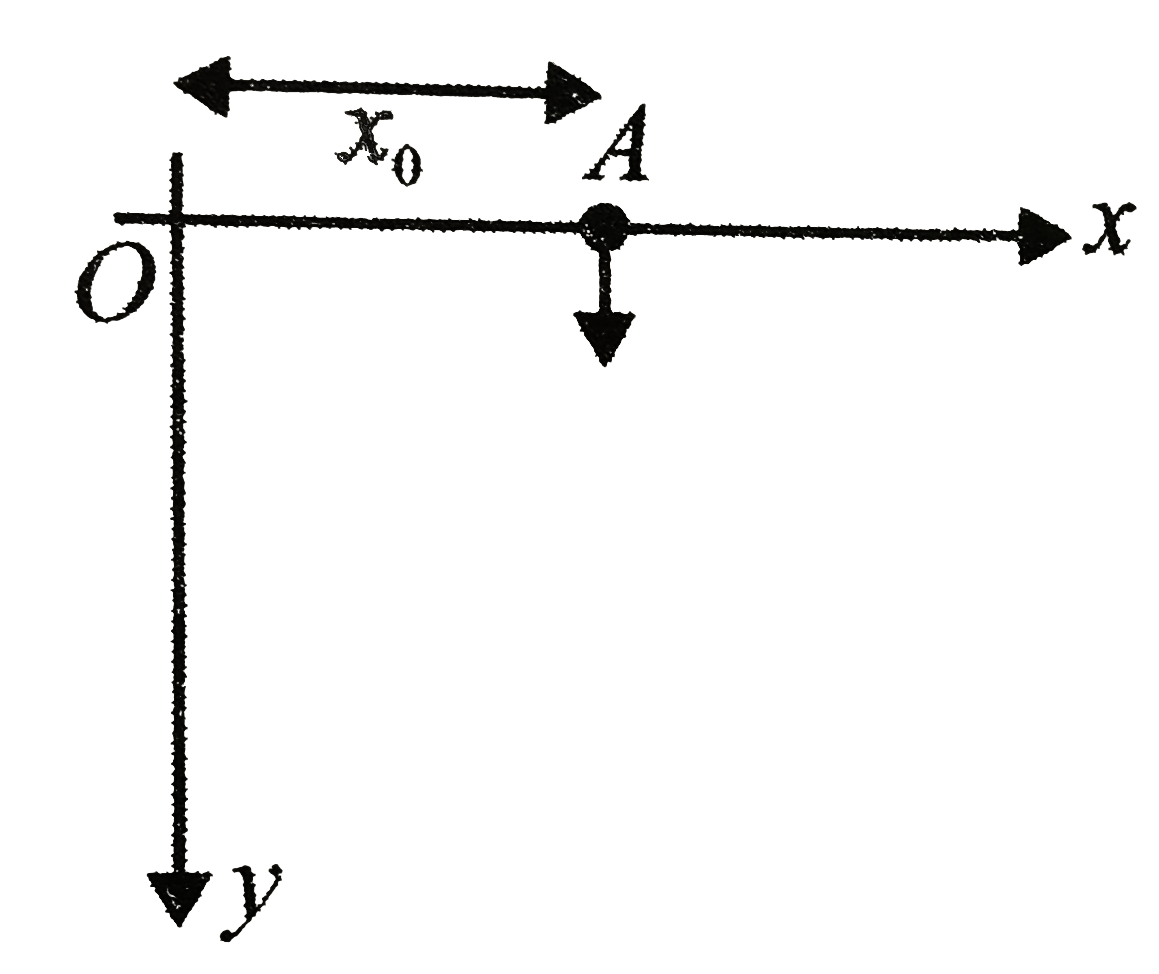
View SolutionA particle of mass `m` is released from rest at point `A` in Fig., falling parallel to the (vertical) `y`-axis. Find the angular momentum of the particle at any time `t` with respect to the same origin `O`.
View SolutionDiscs `A` and `B` are mounted on a shaft `SS` and may be connected or disconnected by a clutch `C`. The moment of inertia of disc `A` is one half that of disc `B`. With the clutch disconnected, `A` is brought up to an angular velocity `omega_(0)` .The accelerating torque is then removed from `A` and it is coupled to disc `B` by the clutch (Bearing friction may be neglected). It is found that `2000 J` of heat is developed in the clutch when the connection is made. What is the original kinetic energy of disc `A`?
View Solution
A cicular disc of mass `m` and radius `R` is set into motion on a horizontal floor with a linear speed `v` in the forward direction and an angular speed `omega=(v)/(R)` in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point `O` of the disc.
View SolutionA particle of mass `m` is projected with a speed `u` at an angle `theta` to the horizontal at time `t = 0`. Find its angular momentum about the point of projection `O` at time `t`, vectorially. Assume the horizontal and vertical lines through `O` as `X` and `Y` axes, respectively.
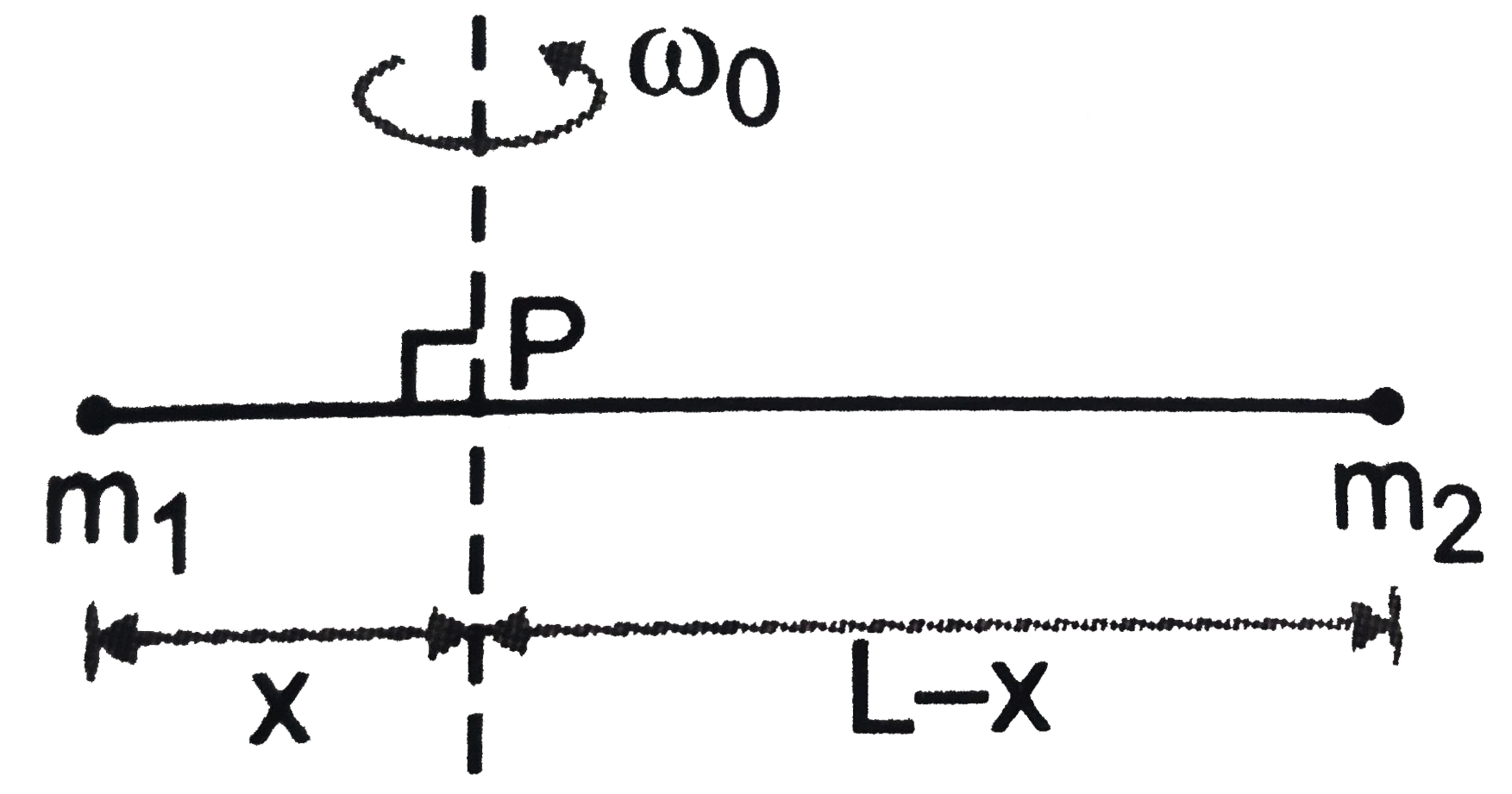
View SolutionPoint masses `m_(1) and m_(2)` are placed at the opposite ends of a rigid rod of length `L`, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point `P` on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity `omega_(0)` is minimum, is given by :
View SolutionA thin uniform circular disc of mass `M` and radius `R` is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega`. Another disc of the same dimensions but of mass `M//4` is placed gently on the first disc co-axially. show that angular velocity o fthe system is `4 omega//5`.
View SolutionA thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass `0.5 kg` is tied and a block of mass `8.0 kg` is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from `8.0 kg` to `1.0 kg`, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?

View SolutionA girl jumps from a height `h` on the end of a see-saw. The see-saw consists of a uniform plank of length `I` pivoted at its centre. The plank is horizontal before the girl jumps. The mass of the see-saw is twice the mass of the girl. Find the angular velocity of the plank just after the girl jumps on the plank.
View SolutionThe device shown in Fig. rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass `m`. Initial angular velocity of the system is `omega_(0)`. Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become `2a`. Initially, it was a. What will be the new angular velocity of the system?
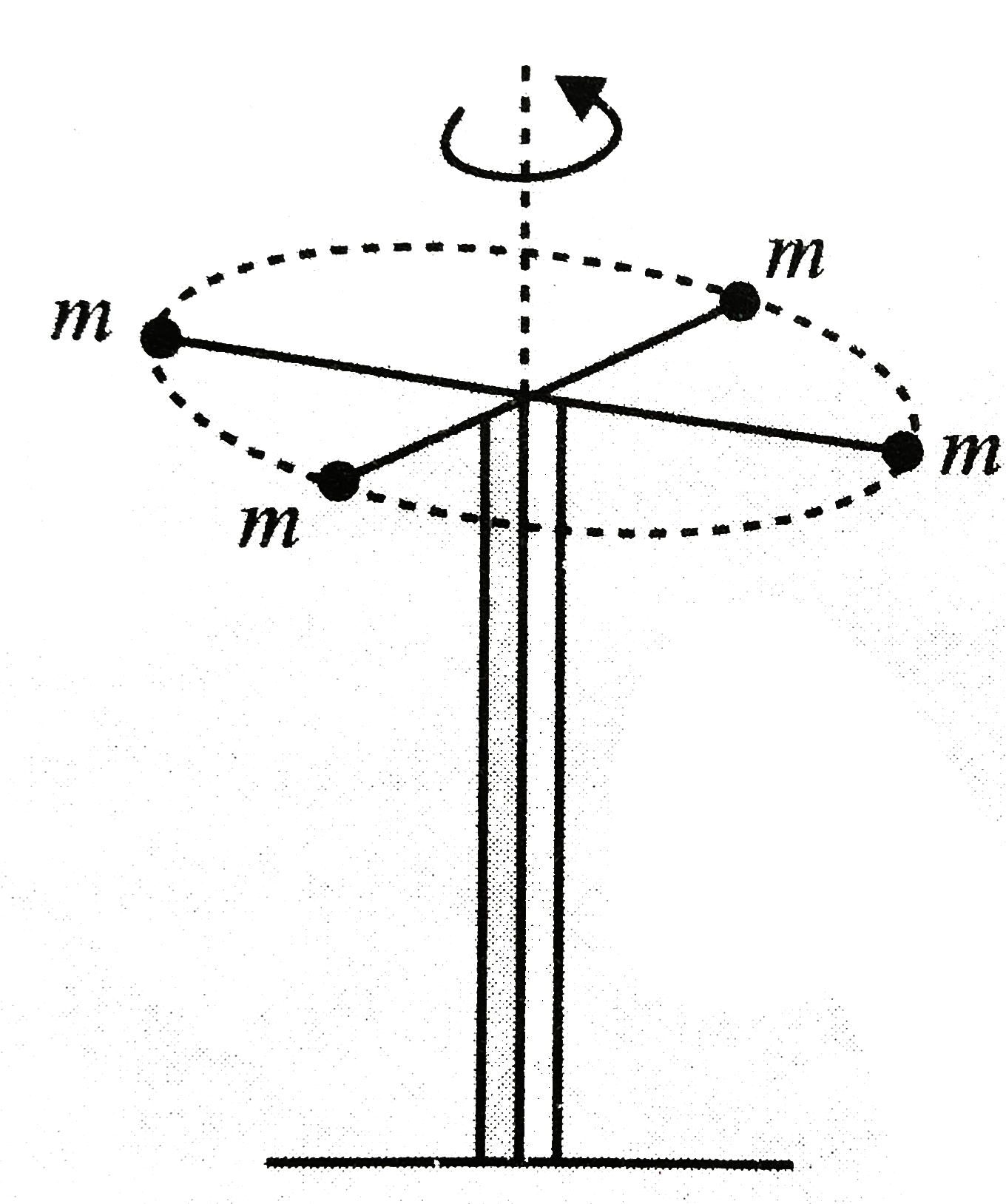
View Solution
Exercise 3.2 questions and complete solutions for chapter RIGID BODY DYNAMICS 2 of CENGAGE PHYSICS (HINGLISH) of Class 11