Complete Solutions to Single Correct of chapter RIGID BODY DYNAMICS 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A uniform ball of radius `r` rolls without slipping down from the top of a sphere of radius `R` Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA solid sphere rests on a horizontal surface. A horizontal impulse is applied at height `h` from centre. The sphere starts rolling just after the application of impulse. The ratio `h//r` will be
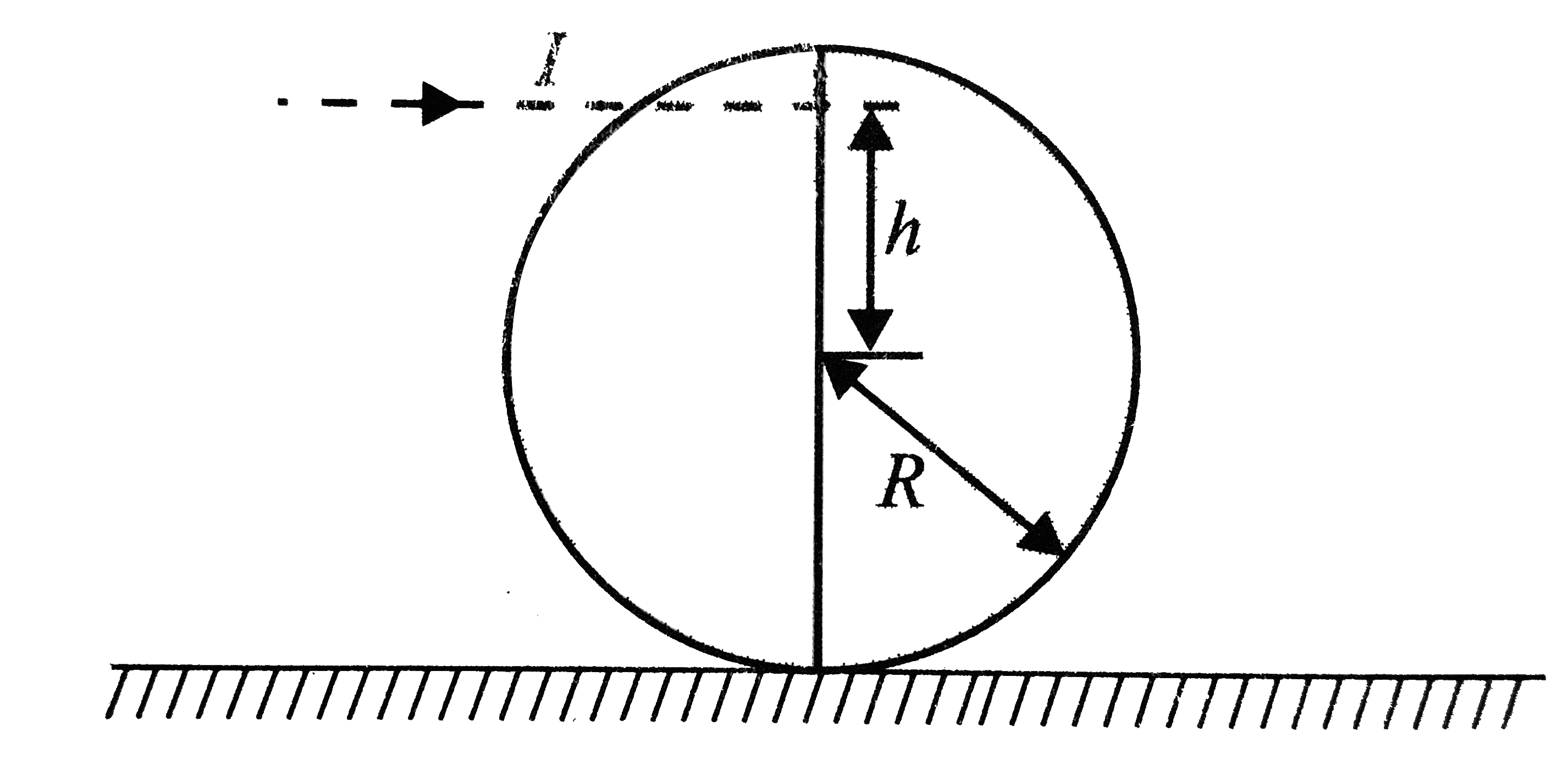
View SolutionIn Fig a sphere of radius `2 m` rolls on a plank. The accelerations of the sphere and the plank are indicated. The value of `alpha` is

View SolutionA ring of radius `R` is first rotated with an angular velocity `omega` and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is `mu`. Time after which its angular speed is reduced to half is
View SolutionTwo bodies with moment of inertia `I_1` and `I_2 (I_1 gt I_2)` have equal angular momenta. If their kinetic energy of rotation are `E_1` and `E_2` respectively, then.
View SolutionIn Fig. the velocities are in ground frame and the cylinder is performing pure rolling on the plank, velocity of point `'A'` would be
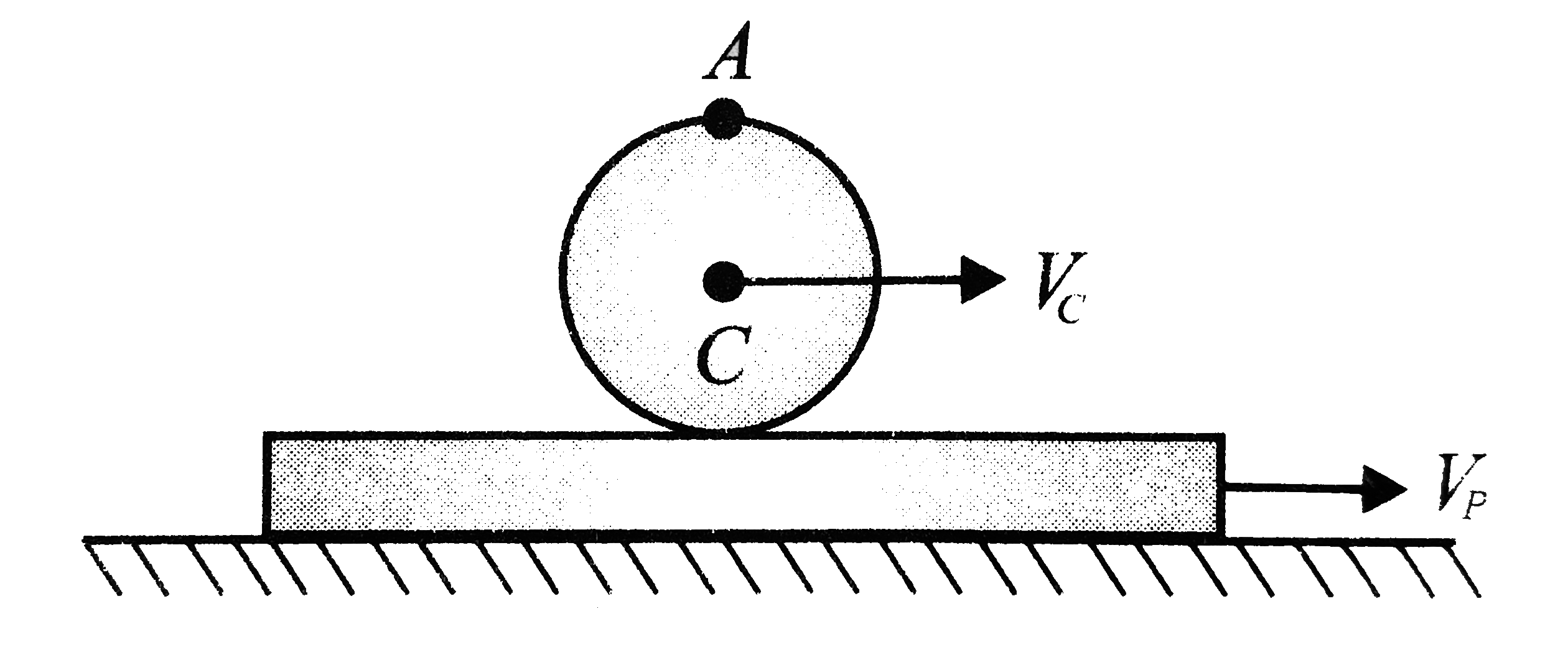
View SolutionA sphere has to purely roll upwards. At an instant when the velocity of sphere is `v,` frictional force acting on it is

View SolutionA string is wrapped around a cylinder of mass `M` and radius `R`. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity `omega_0` about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA uniform thin rod of length `l` and mass `m` is hinged at a distance `l//4` from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then

View SolutionA uniform circular disc of mass `M` and radius `R` rolls without slipping on a horizontal surface. If the velocity of its centre is `v_0`, then the total angular momentum of the disc about a fixed point `P` at a height `(3R)//2` above the centre `C`.

View SolutionA child is standing with folded hands at the center of a platform rotating about its central axis. The kinetic energy of the system is `K`. The child now stretches his arms so that the moment of inertia of the system doubles. The kinetic energy of the system now is
View SolutionA yo-yo is placed on a rough horizontal surface and a constant force `F`, which is less than its weight, pulls it vertically. Due to this
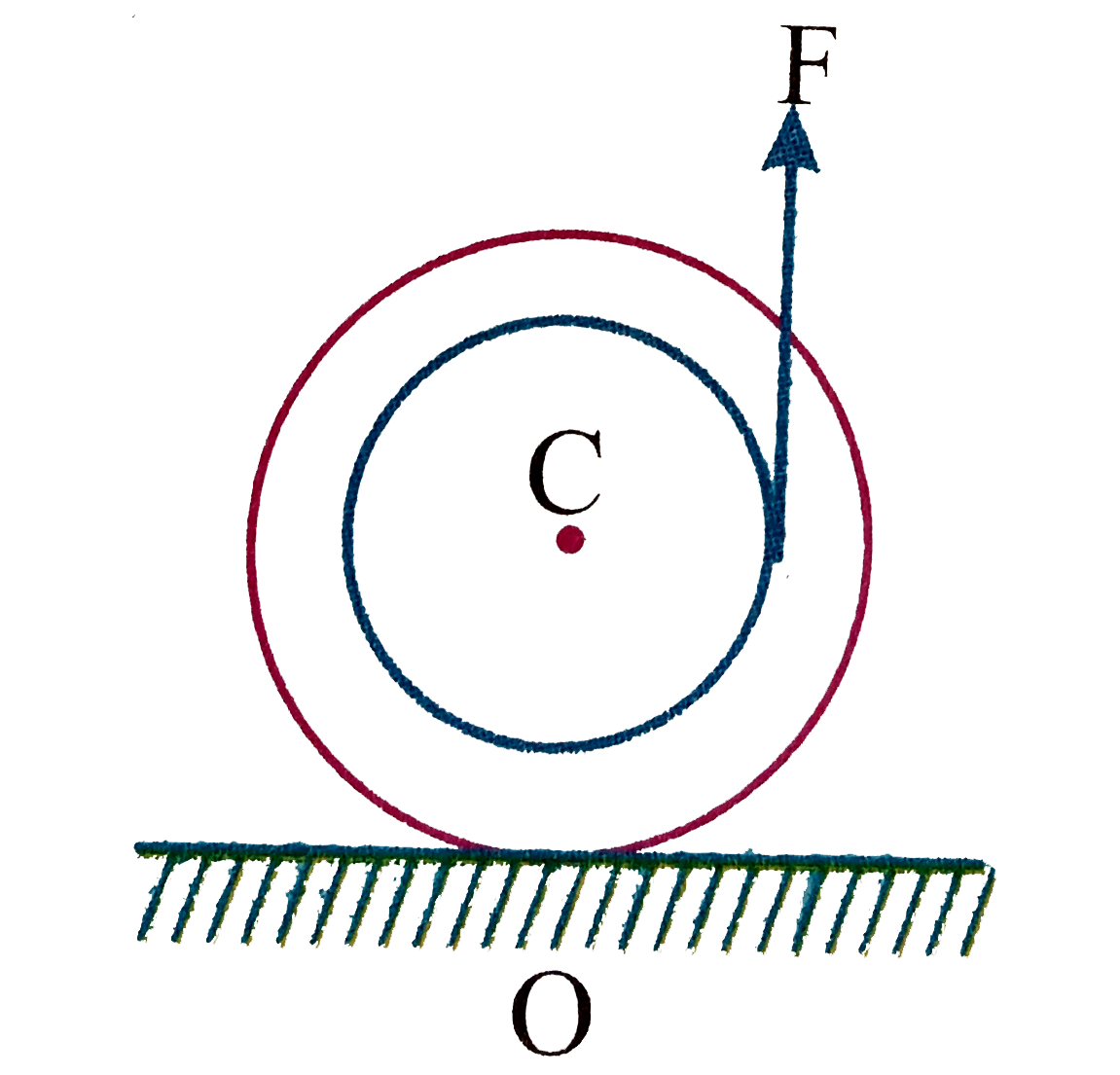
View SolutionA ring, cylinder and solid sphere are placed on the top of a rough incline on which the sphere can just roll without slipping. When all of them are released at the same instant from the same position, then
View SolutionIf a spherical ball rolls on a table without slipping, the fraction of its total energy associated with rotation is
View SolutionA disc of mass `m` and radius `R` moves in the `x-y` plane as shown in Fig. The angular momentum of the disc about the origin `O` at the instant shown is

View Solution
A spool is pulled horizontally on rough surface by two equal and opposite forces as shown in the figure. Which of the following statements are correct?
View SolutionA uniform sphere of mass `m` radius `r` and moment of inertia `I` about its centre moves along the `x`-axis as shown in Fig Its centre of mass moves with velocity `= v_(0)`, and it rotates about its centre of mass with angular velocity `=omega_(0)`. Let `vecL=(Iomega_(0)+mv_(0)r)(-k)`. The angular momentum of the body about the origin `O` is

View SolutionAn impulse `J = mv` at one end of a stationary uniform frictionless rod of mass `m` and length `l` which is free to rotate in a gravity-free space. The impact is elastic. Instantaneous axis of rotation of the rod will pass through
View SolutionA solid sphere of mass `m` is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is `mu`. The maximum value of `F`, so that the sphere will not slip, is equal to

View SolutionA uniform rod `AB` of length `l` and mass `m` hangs from point `A` in a car moving with velocity `v_(0)` on an inclined plane as shown in Fig. The rod can rotate in vertical plane about the axis at point `A`. if the car suddenly stops, the angular speed with which the rod starts rotating is
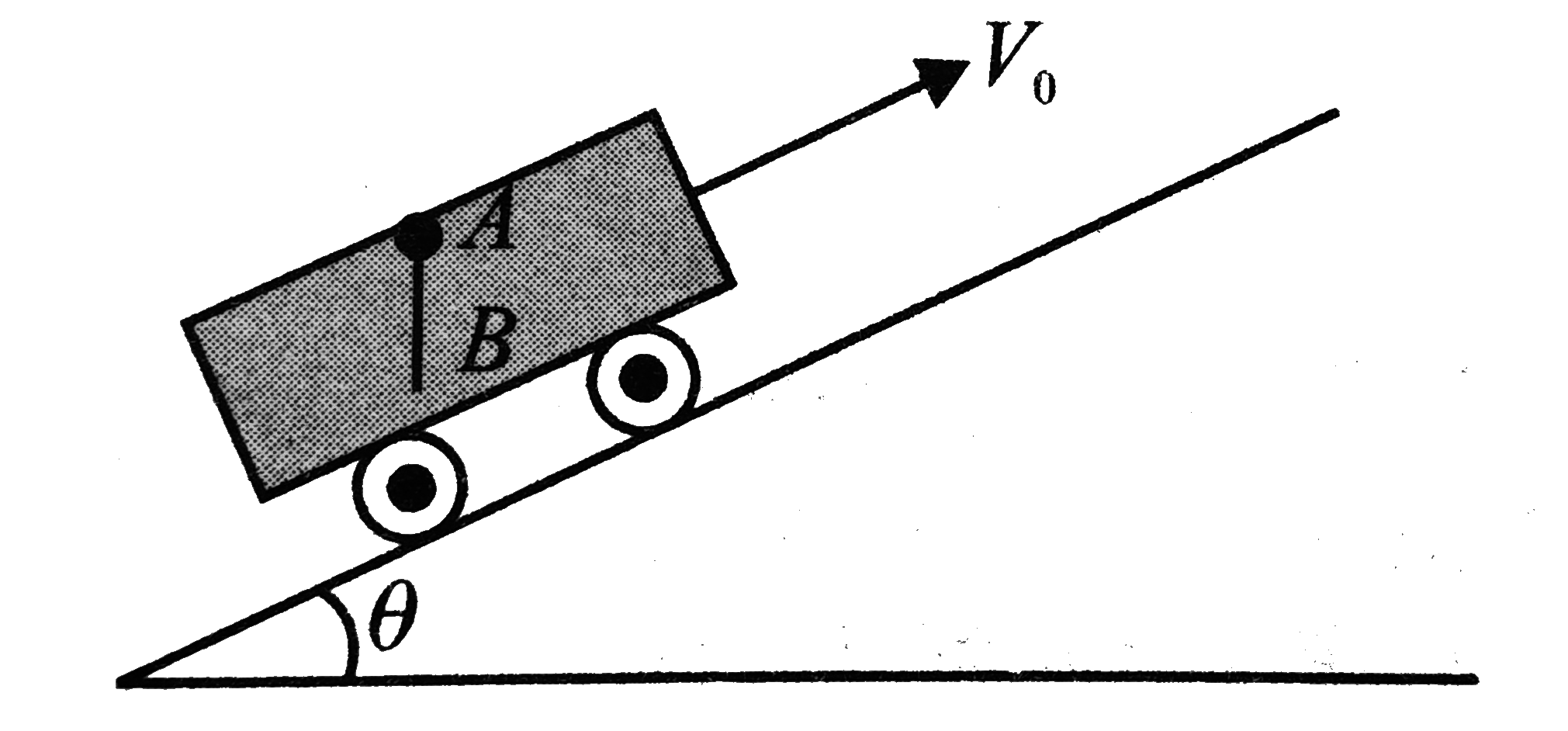
View SolutionA uniform rod of mass `m`, length `l` rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse `p` perpendicular to the rod at a distance `l//4` from the centre. The angular velocity of the rod will be
View SolutionA thin plate of mass `M`,length `L` and width `2d` is mounted vertically on a frictionless fixed axle along the `z`-axis as shown. Initially, the object is at rest. it is then tapped with a hammer to provide a torque `tau`, which produces an angular impulse `H` about the z-axis of magnitude `H = int tau dt`. What is the angular speed co of the plate about the `z`-axis after the tap?

View SolutionA uniform circular disc of radius `r` is placed on a rough horizontal surface and given a linear velocity `v_(0)` and angular velocity `omega_(0)` as shown. The disc comes to rest after moving some distance to the right. It follows that

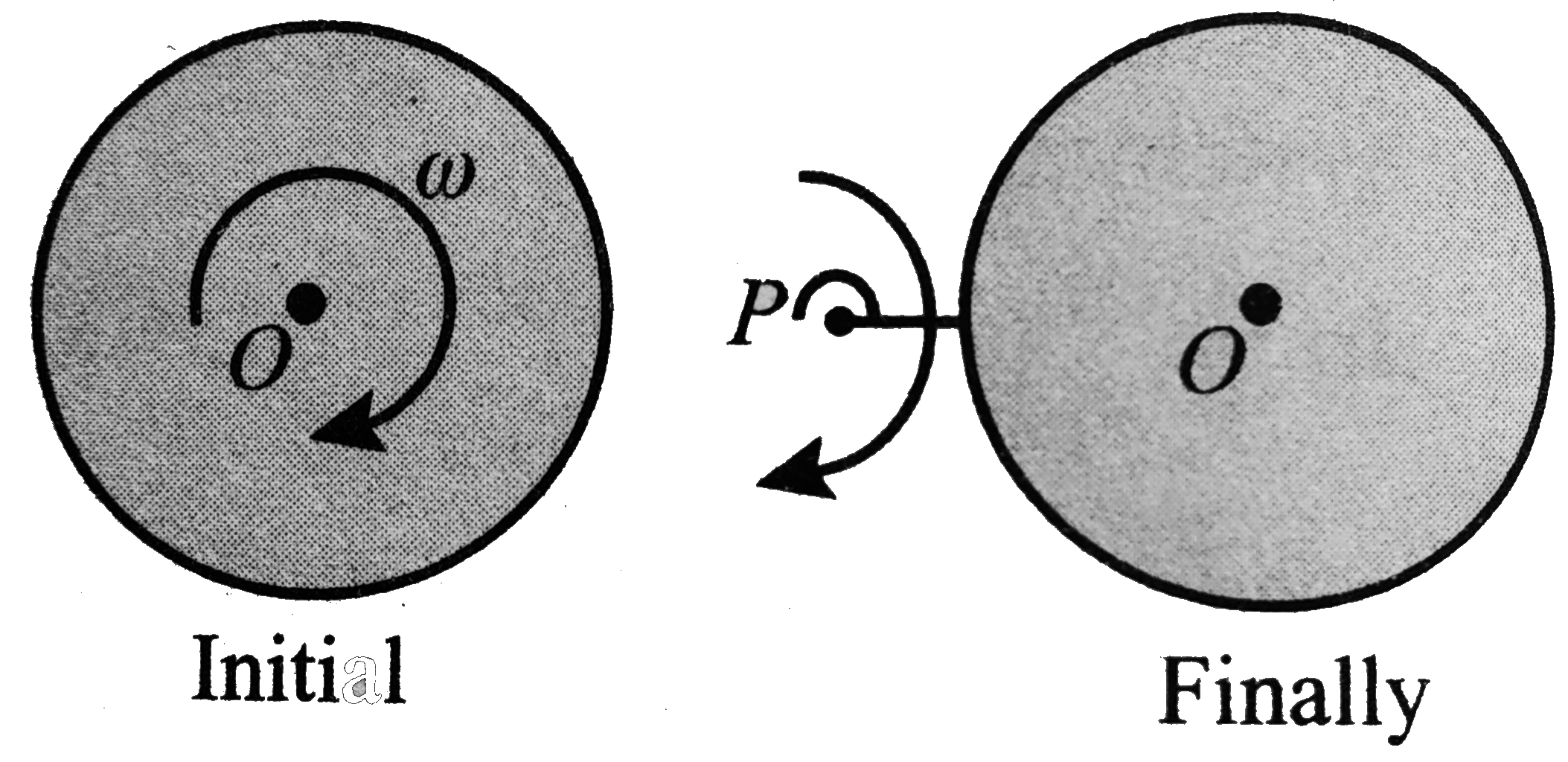
View SolutionA disc is freely rotating with an angular speed `omega` on a smooth horizontal plane. If it is hooked at a rigid pace `P` and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
View SolutionA small solid sphere of radius `r` rolls down an incline without slipping which ends into a vertical loop of radius `R`. Find the height above the base so that it just loops the loop
View SolutionA sphere is rolling down an inclined plane without slipping. The ratio of rotational kinetic energy to total kinetic energy is
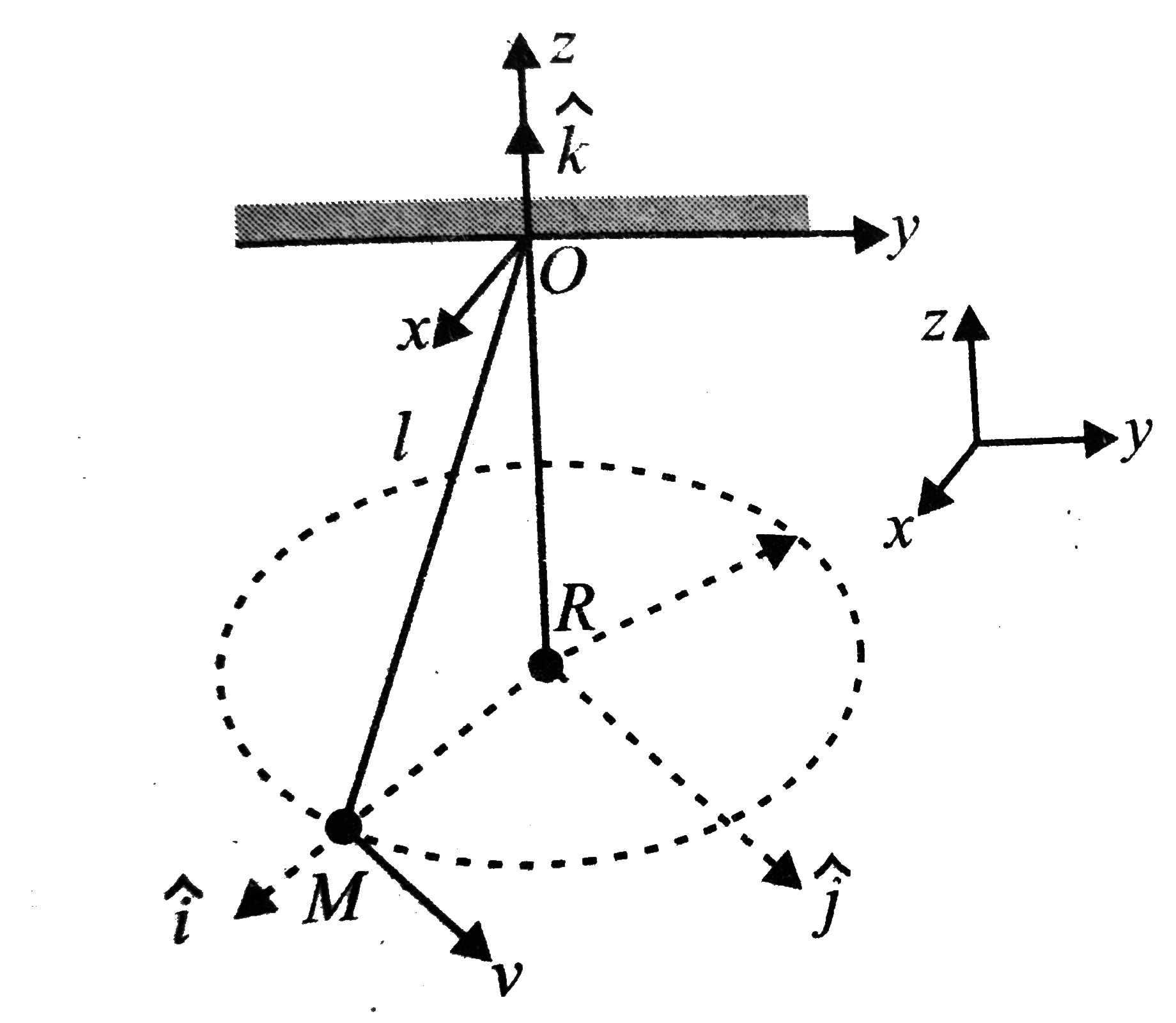
View SolutionA conical pendulum consists of a mass `M` suspended from a strong sling of length `l`. The mass executes a circle of radius `R` in a horizontal plane with speed `v`. At time `t`, the mass is at position `Rhati` and `vhatj` velocity. At time `t` the angular momentum vector of mass `M` about the point from which the string passes on the ceiling is
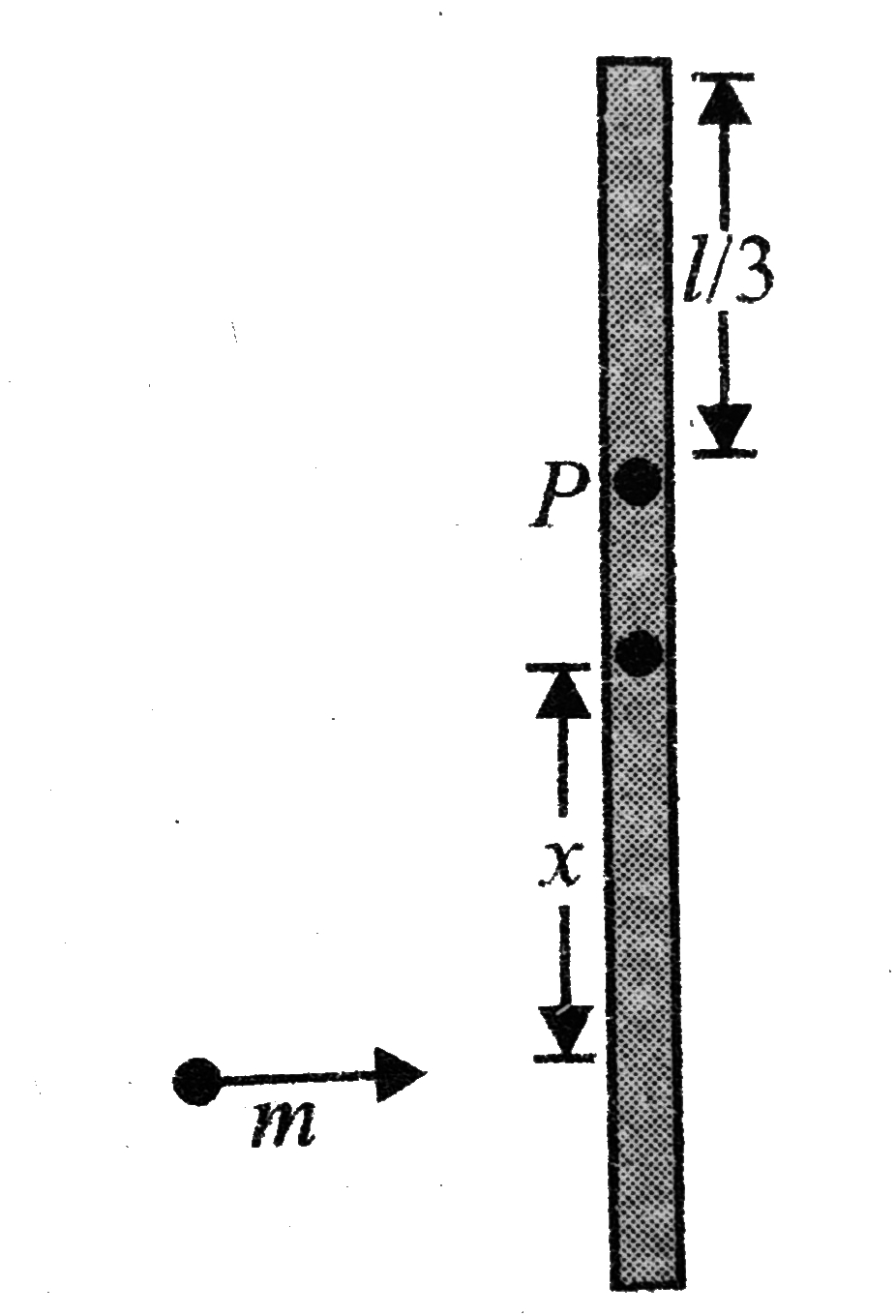
View SolutionA thin uniform rod of mass `m` and length `l` is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass `m` strike on the rod such that the point `P` at a distance `l/3` from the end of the rod is instantaneously at rest just after the elastic collision?
View SolutionA yo-yo, arranged as shown, rests on a frictionless surface. When a force `F` is applied to the string, the yo-yo
View SolutionVelocity of the centre of a small cylinder is `v`. There is no slipping anywhere. The velocity of the centre of the larger cylinder is

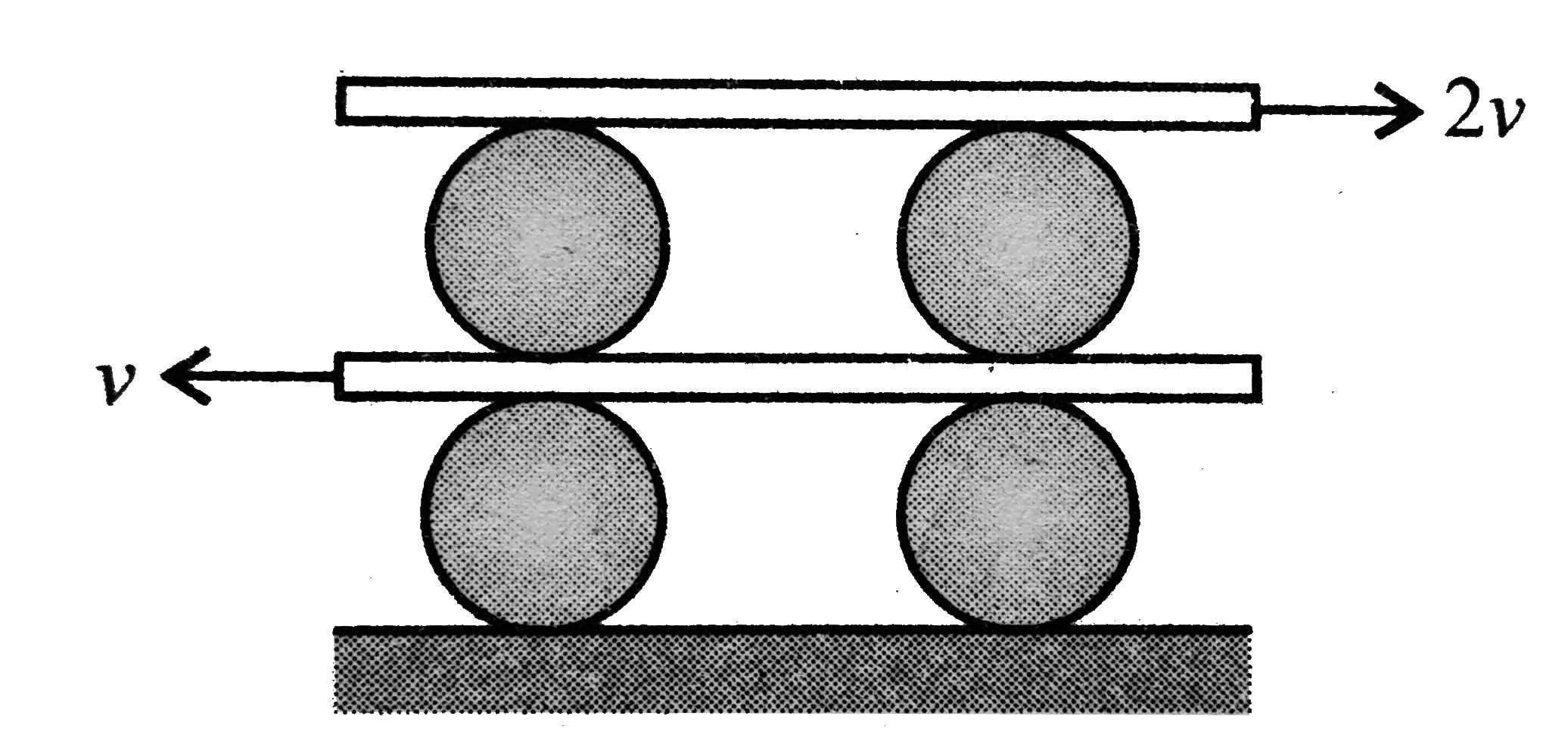
View SolutionA system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are `V` and `2V`, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
View SolutionThe spool shown in the figure is placed on a rough horizontal surface and has inner radius `r` and outer radius `R`. The angle `theta` between the applied force and the horizontal can be varied. The critical angle `theta` for which the spool does not roll and remains stationary is given by

View SolutionA small bead of mass `m` moving with velocity `v` gets threaded on a stationary semicircular ring of mass `m` and radius `R` kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

View SolutionA block of mass `m` is attached to a pulley disc of equal mass, radius `r` by means of a slack string as shown. The pulley is hinged about its centre on a horizontal table and the block is projected with an initial velocity of `5 m//s`. Find the velocity when the string becomes taut.
 .
.
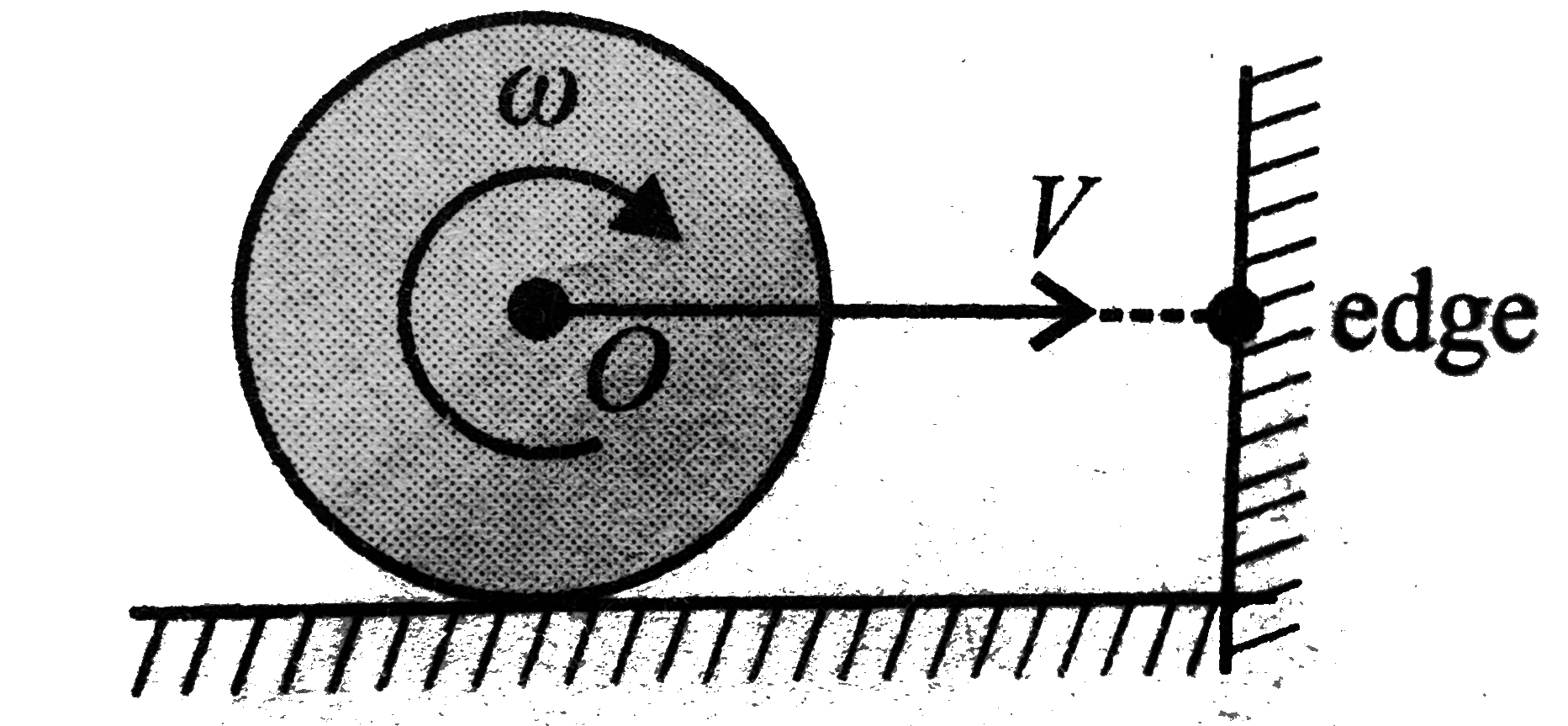
View SolutionA uniform solid sphere of radius `r` is rolling on a smooth horizontal surface with velocity `V` and angular velocity `omega=(V=omegar)`. The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge `mu = 1//5`. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
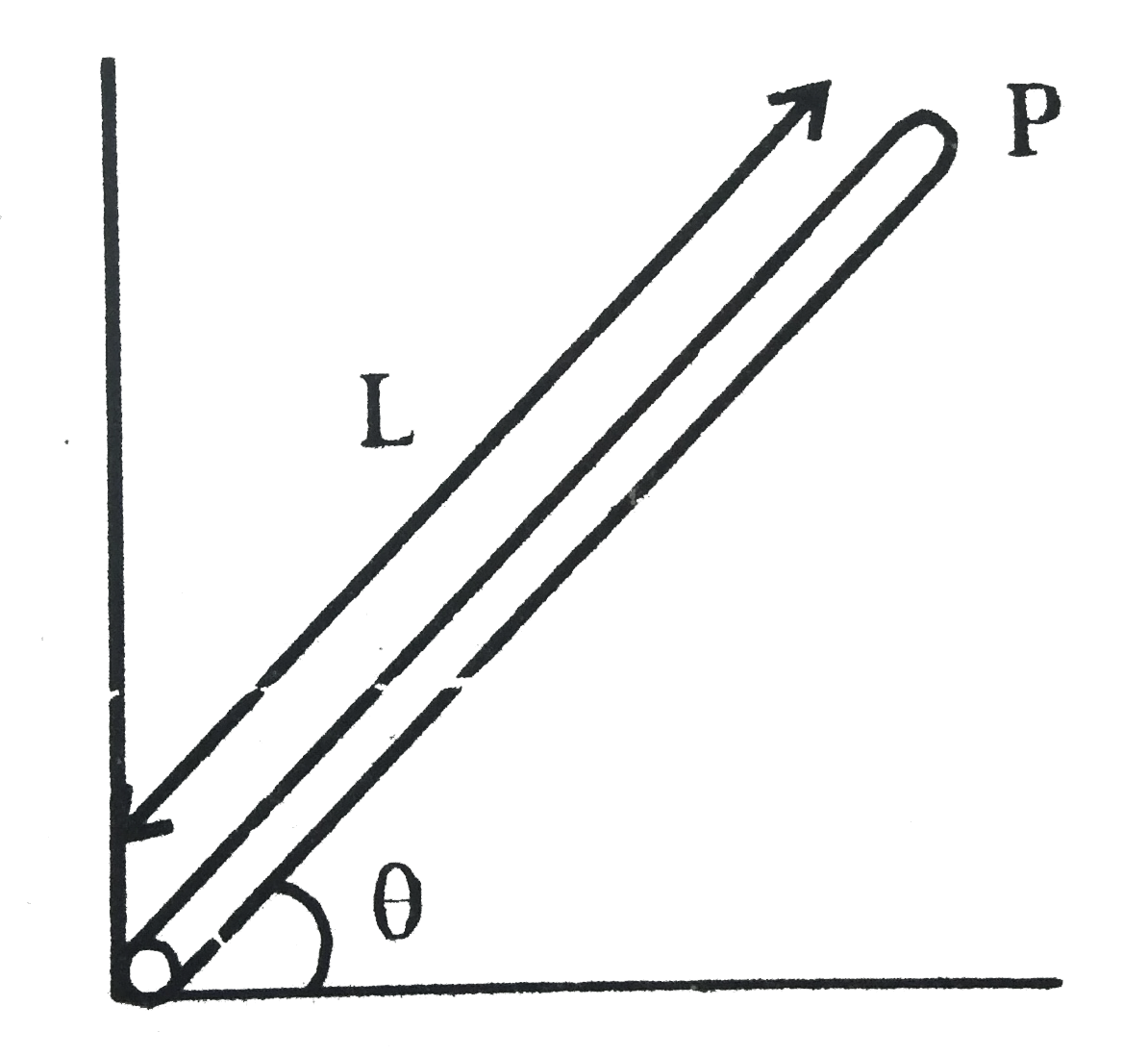
View SolutionA uniform flag pole of length `L ` and mass `M` in pivoted on the ground with a frictionless hinge. The flag pole makes an angle `theta` with the horizontal. The moment of inertia of the flag pole about one end is `(1//3) ML^(2)`. If starts falling from the position shown in figure, the linear acceleration of the free end of the flag pole-labeled `P` - would be.
 .
.
View SolutionIn the figure shown, a ring `A` is initially rolling without sliding with a velocity `v`, on the horizontal surface of the body `B` (of same mass as `A`). All surfaces arc smooth. `B` has no initial velocity. What will be the maximum height reached by `A` on `B`?

View SolutionTwo points of a rod move with velocity `3 v` and `v` perpendicular to the rod and in the same direction. Separated by a distance `r`. Then the angular velocity of the rod is :
View SolutionA sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
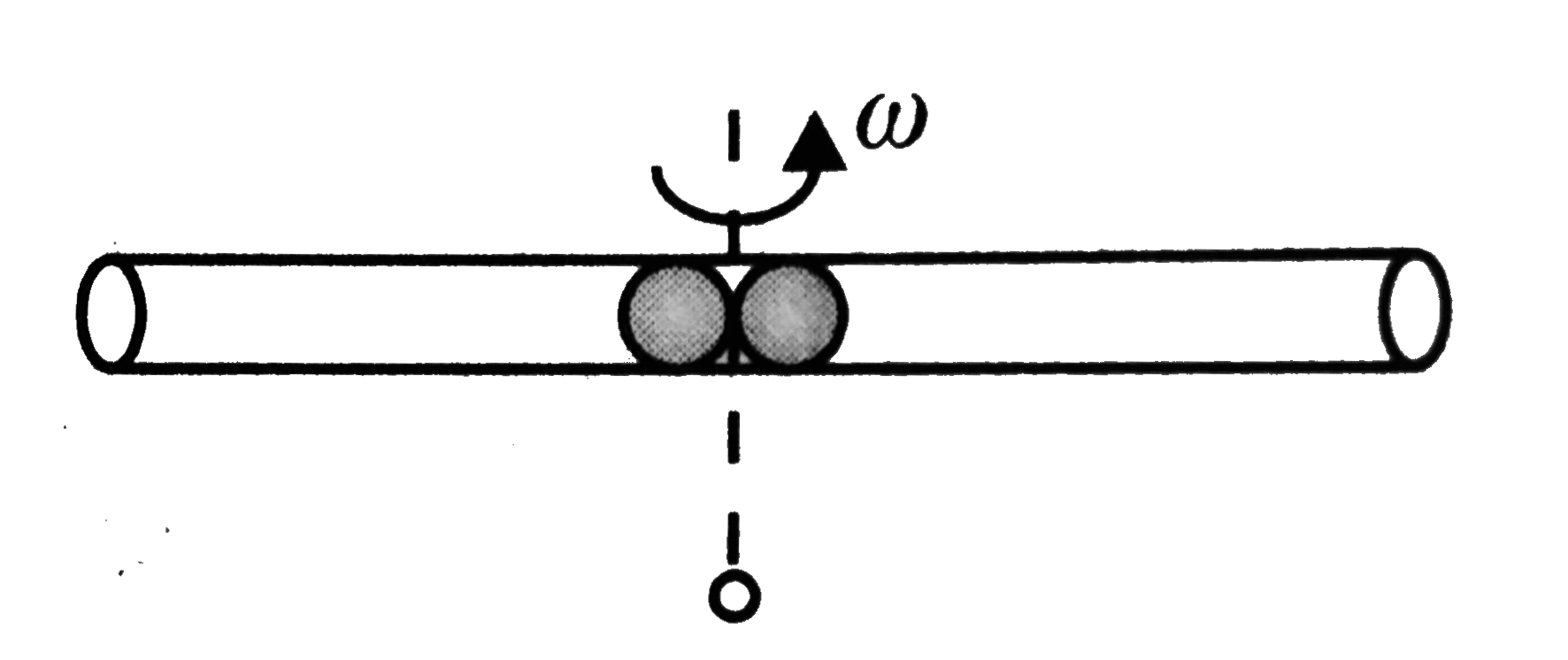
View SolutionA smooth tube of certain mass is rotated in a gravity-free Space and released. The two balls shown in Fig move towards the ends of the tube. For the whole system, which of the following quantities is not conserved.
View SolutionIn the figure shown, a ball without sliding on a horizontal, surface. It ascends a curved track up to height `h` returns. The value of h is `h_(1)` for sufficiently rough curved track to avoid sliding and is `h_(2)` for smooth curved track then
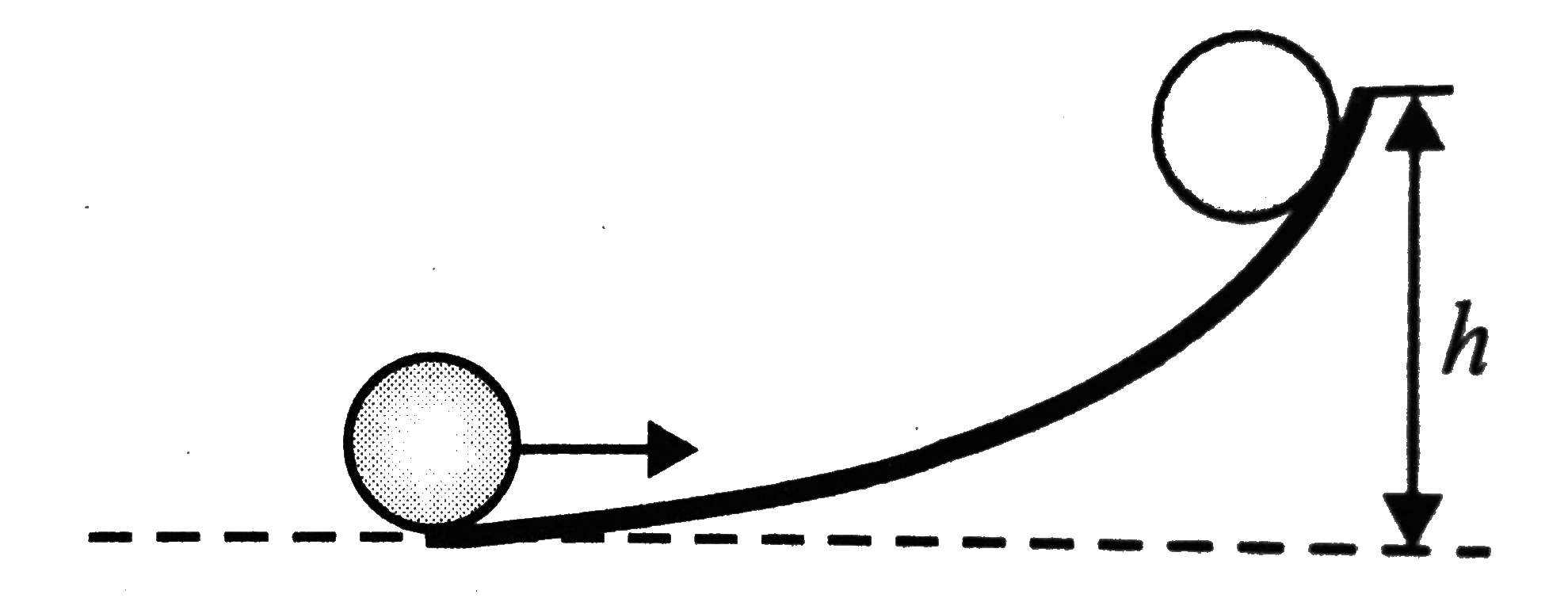
View SolutionA ring of radius `R` rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
 .
.
View SolutionA uniform ring of radius `R` is given a back spin of angular velocity `V_(0)//2R` and thrown on a horizontal rough surface with velocity of centre to be `V_(0)`. The velocity of the centre of the ring when it starts pure rolling will be
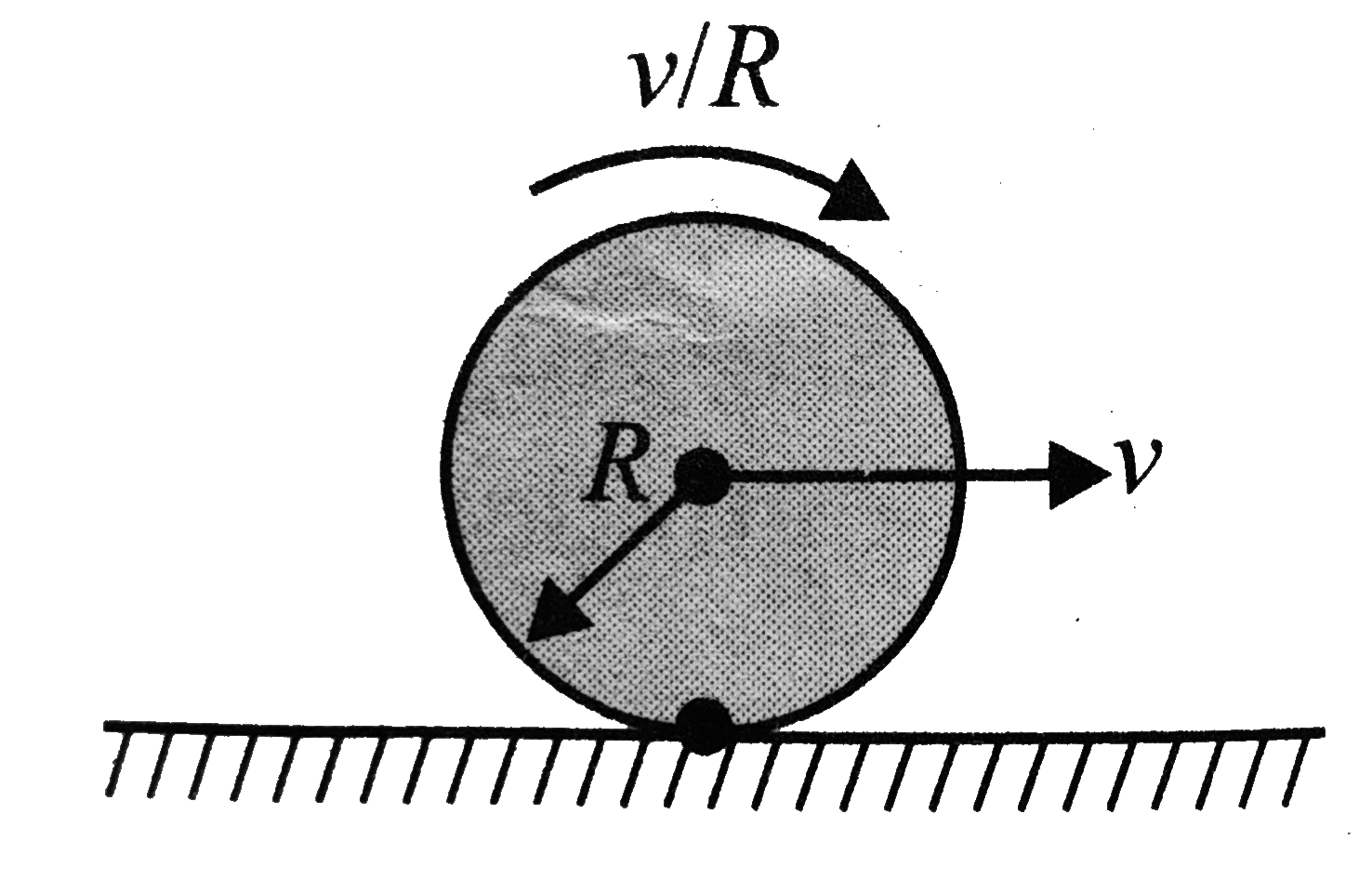
View SolutionA disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in Fig,. At any instant, for the lower most point of the disc,
View SolutionA particle of mass `m` is rigidly attached at `A` to a ring of mass `3m` and radius `r`. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionA uniform smooth rod (mass `m` and length `l`) placed on a smooth horizontal floor is it by a particle (mass `m`) moving on the floor, at a distance `l/4` from one end elastically `(e = 1)`. The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
View SolutionA soldi sphere a hollow sphere and a disc, all haing same mass and radius are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
View SolutionA uniform rod of mass `m` and length `l` is placed over a smooth horizontal surface along the `y`-axis and is at rest as shown in Fig. An impulsive force `F` is applied for a small time `/_\t` along `x`-direction at point `A`. The `x`-coordinate of end `A` of the rod when the rod becomes parallel to `x`-axis for the first time is [initially, the coordinate of centre of mass of the rod is `(0, 0)`]

View SolutionA mass `m` is moving at speed `v` perpendicular to a rod of length `d` and mass `M= 6m` pivots around a frictionless axle running through its centre and stickes to the end of the rod. The moment of inertia od the rod about its centre is `Md^(2)//12`. Then the angular speed of the system right after the collision us -
View SolutionA particle falls freely near the surface of the earth. Consider a fixed point `O` (not vertically below the particle) on the ground.
View SolutionA ball of mass moving with constant velocity `u` collides with a smooth horizontal surface at `O` as shown in Fig. Neglect gravity and friction. The `y`-axis is drawn normal to the horizontal surface at the point of impact `O` and `x`-axis is horizontal as shown. About which point will the angular momentum of ball be conserved?
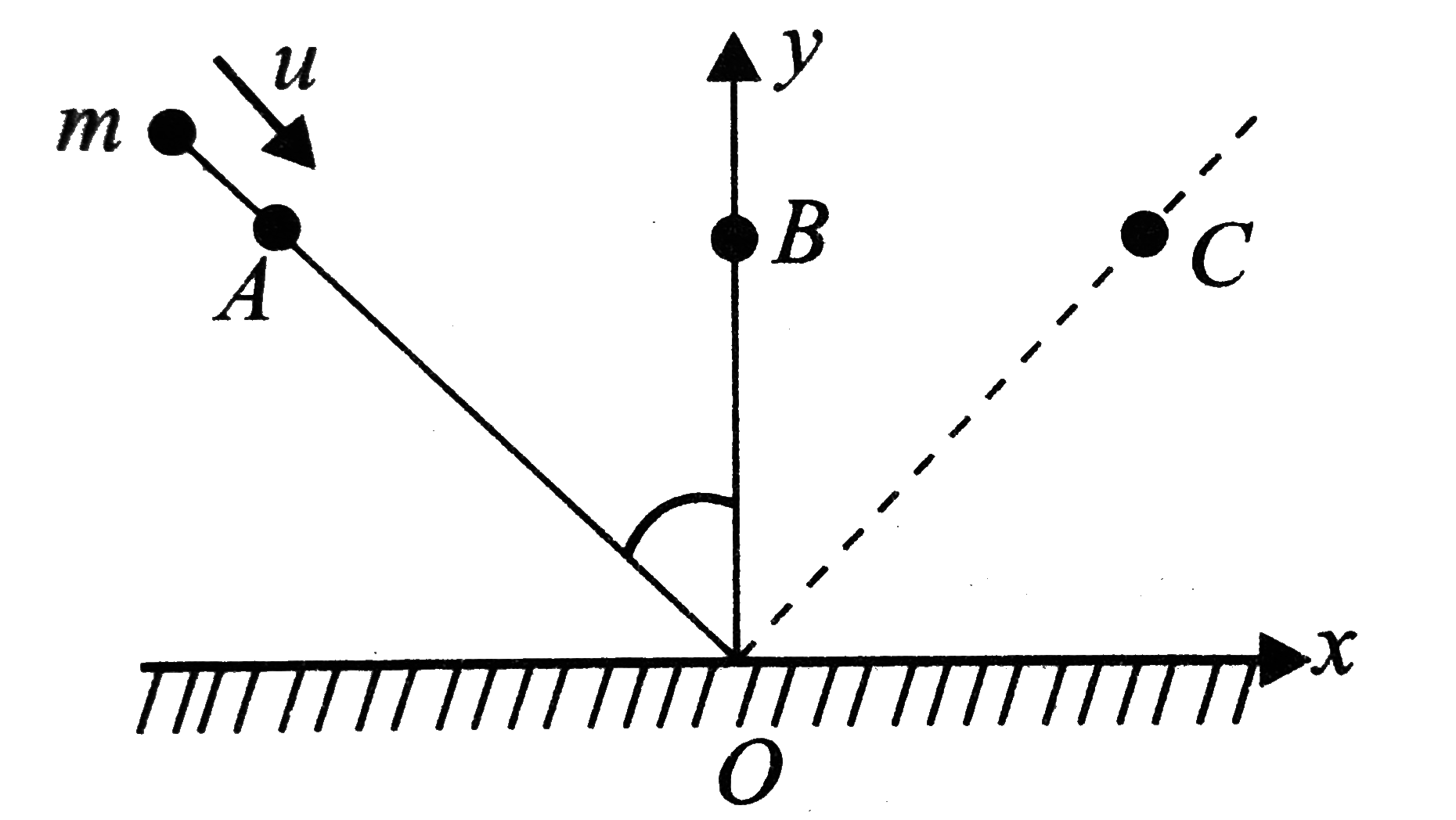
View SolutionA solid sphere of mass `M` and radius `R` is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height `h` above the surface. The value of `h` so that the sphere performs pure rolling motion immediately after it has been stuck is

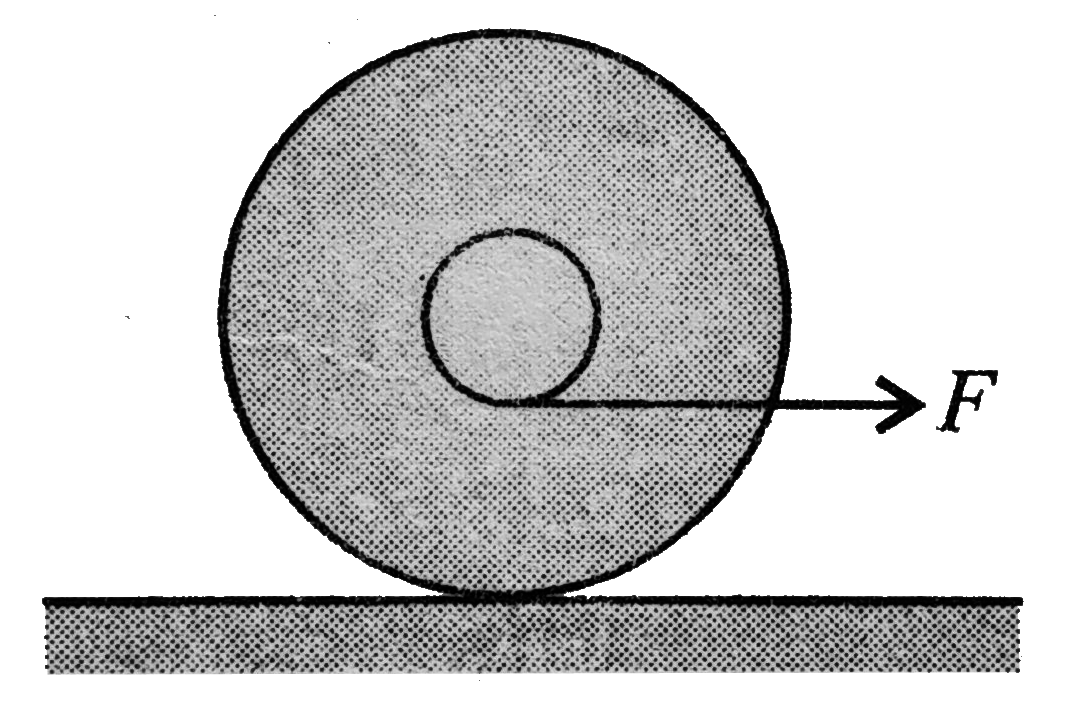
View SolutionAn object of mass `M` and radius `R` is performing pure rolling motion on a smooth horizontal surface under the action of a constant force `F` as shown in Fig. The object may be

View SolutionA uniform rod of mass `M` and length `L` is free to rotate in `X-Z` plane i.e. `vecF=(3hati+2hatj+6hatk)N` is acting on the rod at `(L//2, 0,0)` in the situtation shown in figure. The angular acceleration of the rod is (Take `M=6 kg` and `L=4m`)
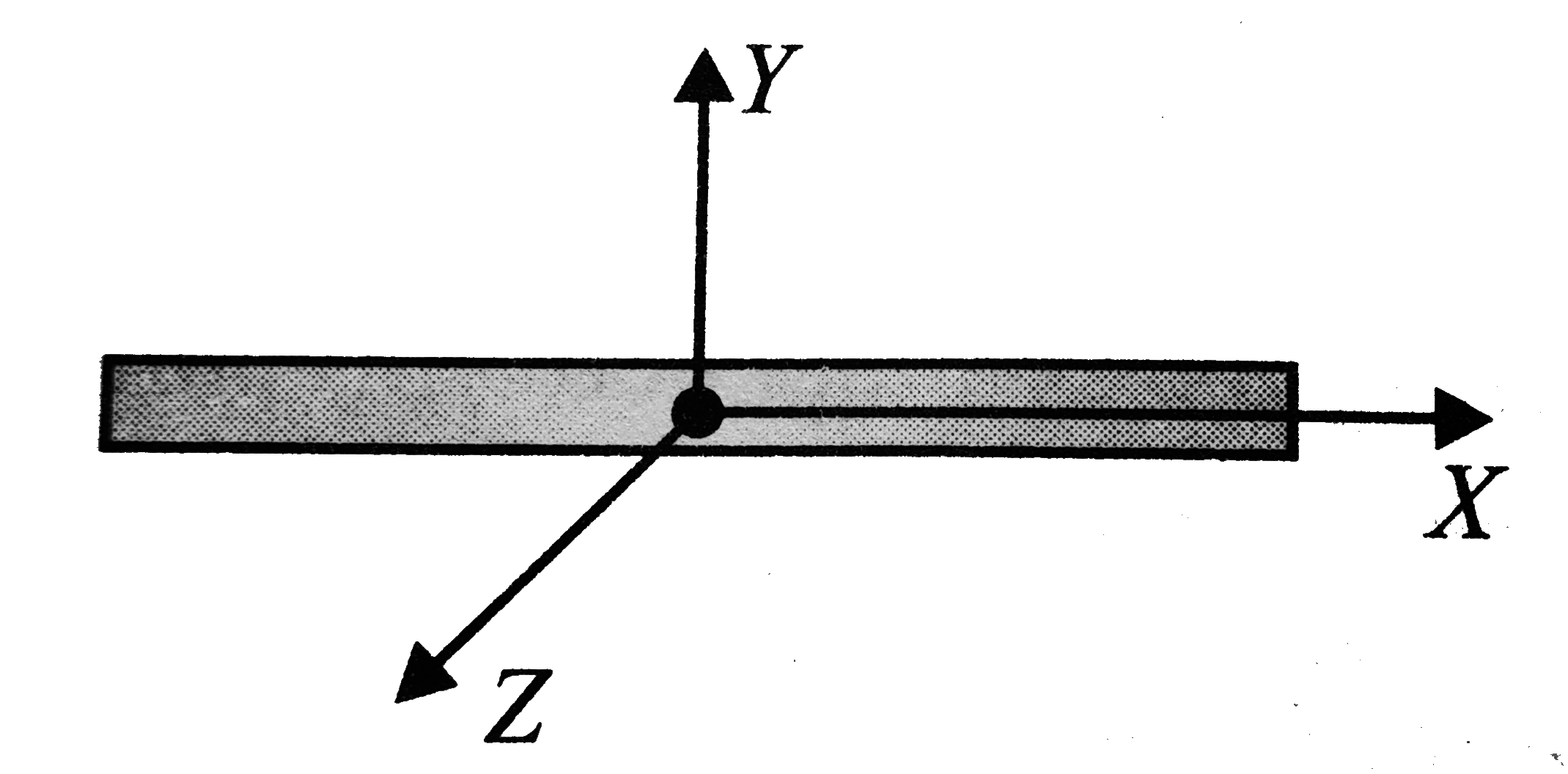
View SolutionA cylinder having moment of inertia, which is free to rotate about its axis, receives an angular impulse of `J kgm^(2)//s` initially, followed by similar impulse after every `4 s`. What is the angular speed of the cylinder `30 s` after the initial impulse?
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)
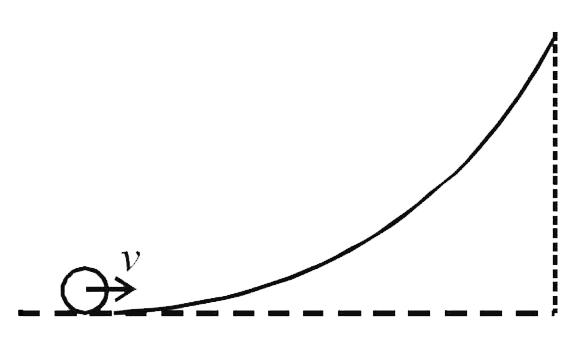
with respect to the initial position. The object is
View SolutionA cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by `x =A cos (omega t).` There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
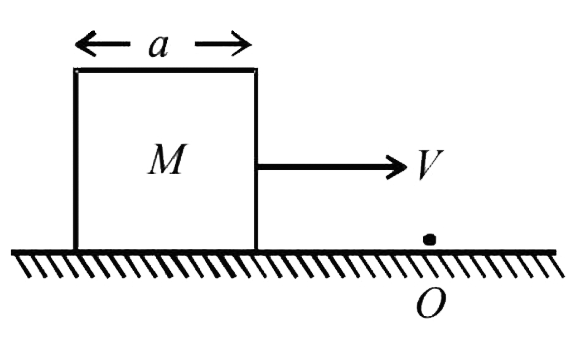
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
View SolutionA solid cylinder is placed on the end of an inclined plane. It is found that the plane can be tipped at an angle `theta` before the cylinder starts to slide. When the cylinder turns on its sides and is allowed to roll, it is found that the steepest angle at which the cylinder performs pure rolling is `phi`. The ratio `tanphi//tantheta` is
View SolutionA uniform box of height `2 m` and having a square base of side `1 m`, weight `150 kg`, is kept on one end on the floor of a truck. The maximum speed with which the truck can round a curve of radius `20 m` without causing the block to tip over is (assume that friction is sufficient is no sliding).
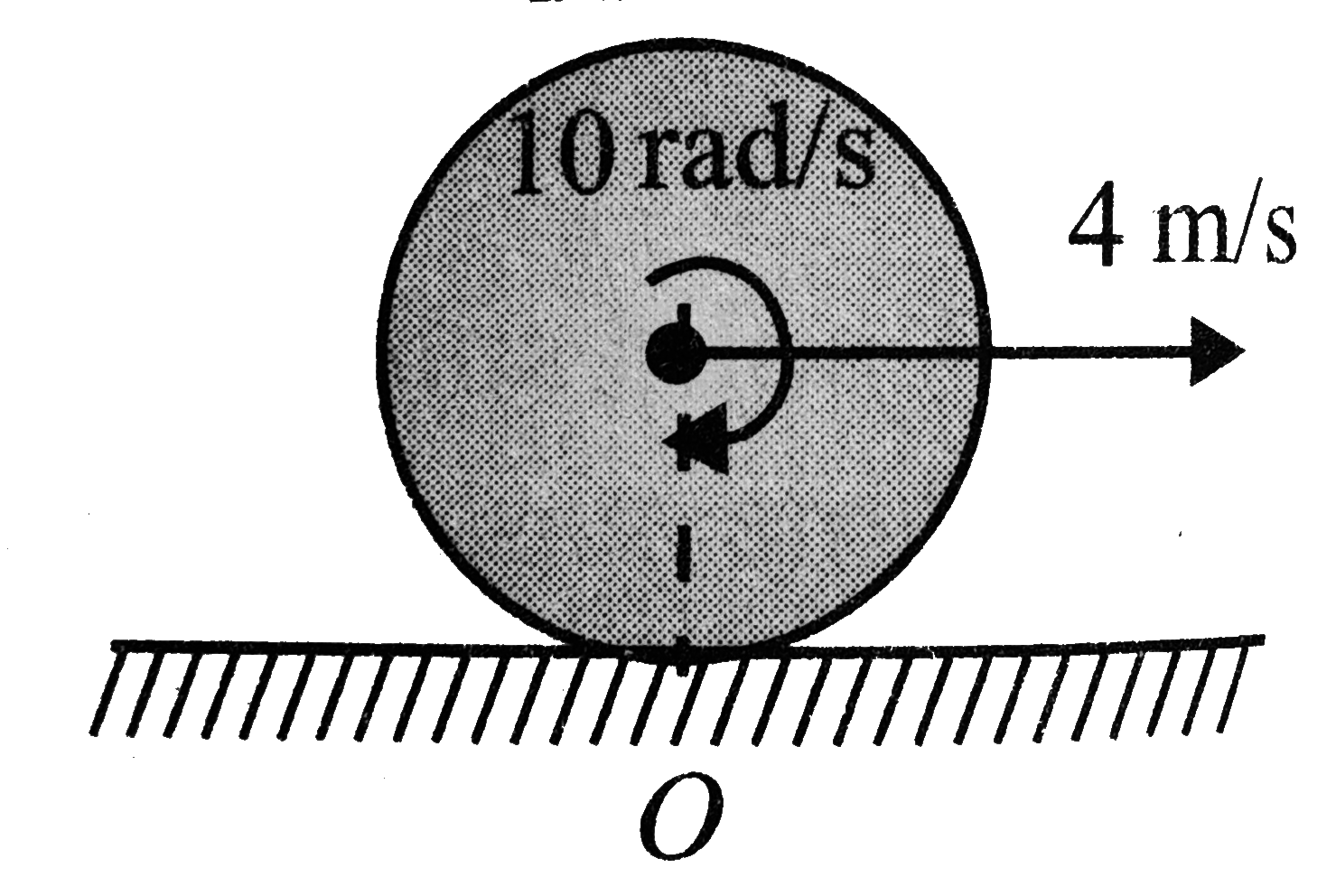
View SolutionA disc of radius `0.2 m` is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is `O` and centre of disc is `C`)
View SolutionA slender rod of mass `M` and length `L` rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse `J` perpendicular to the rod at other end is
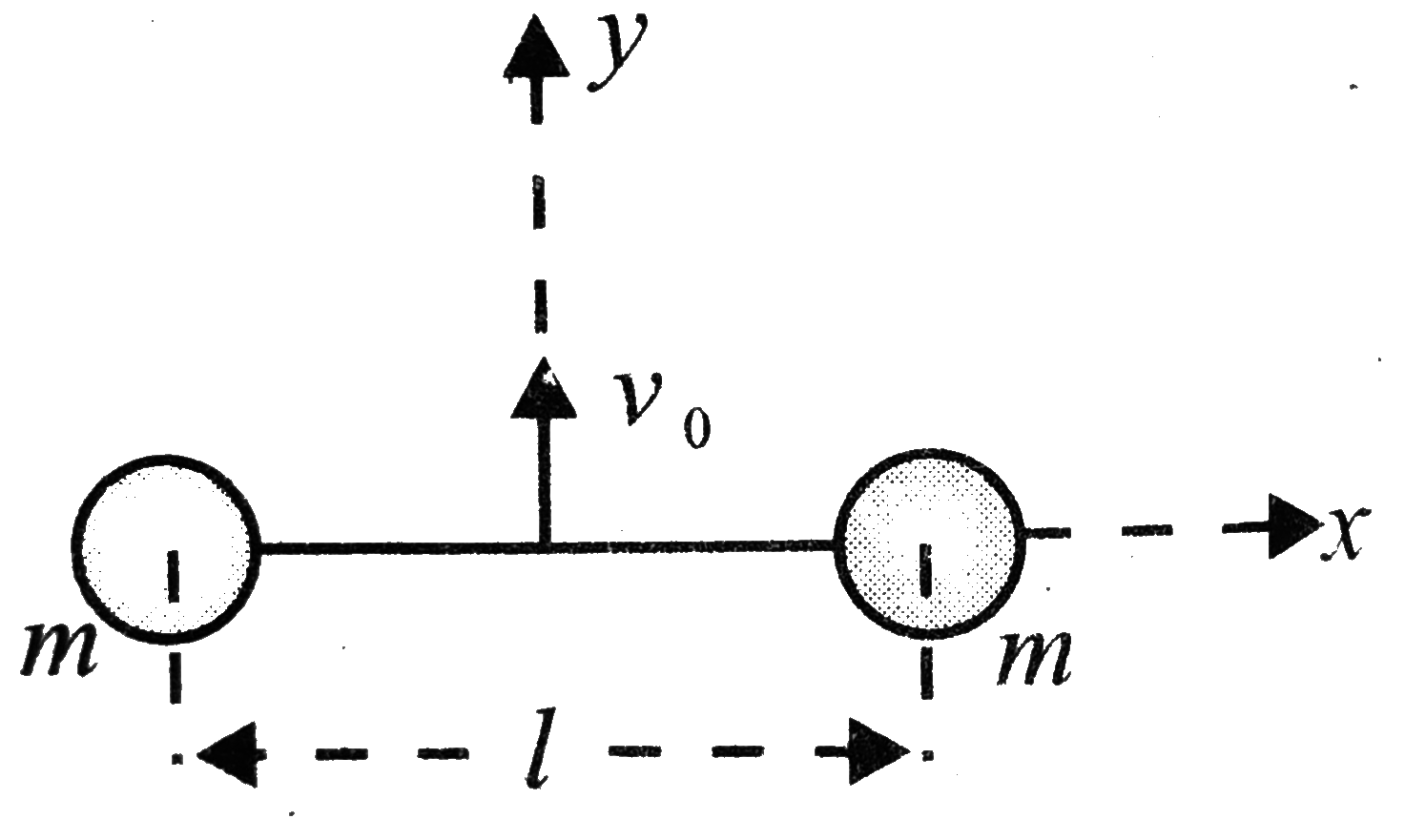
View SolutionTwo identical small balls, each of mass `m`, are connected by a massless and inextensible string of length `l` and placed on a smooth horizontal `xy` plane. An external agent pulling the string from its mid-point along `y`-axis with velocity `v_(0)` as shown in Fig. When the separation between the two balls reduces to `l//2` then the speed of each ball will be
View SolutionA ball is given a velocity `v` and angular velocity such that the ball rolls purely on a plank whose upper surface is rough enough to prevent slipping but lower surface contact with the ground is smooth. No other force is acting on system.
View SolutionA thick walled hollow sphere has outer radius `R`. It down an inclined plane without slipping and its -speed the bottom is `v`. If the inclined plane is frictionless and the sphere slides down without rolling, its speed at the bottom `5v//4`. What is the radius of gyration of the sphere?
View SolutionA uniform disk turns at `2.4 rev//s` around a frictionless axis. A nonrotating rod, of the same mass as the disk and length equal to the disk's diameter is dropped onto the freely spinning disk (see the figure). They then both turn around the axis with their centres superposed. What will be the angular frequency in rev/s of the combination when they start rotating together.
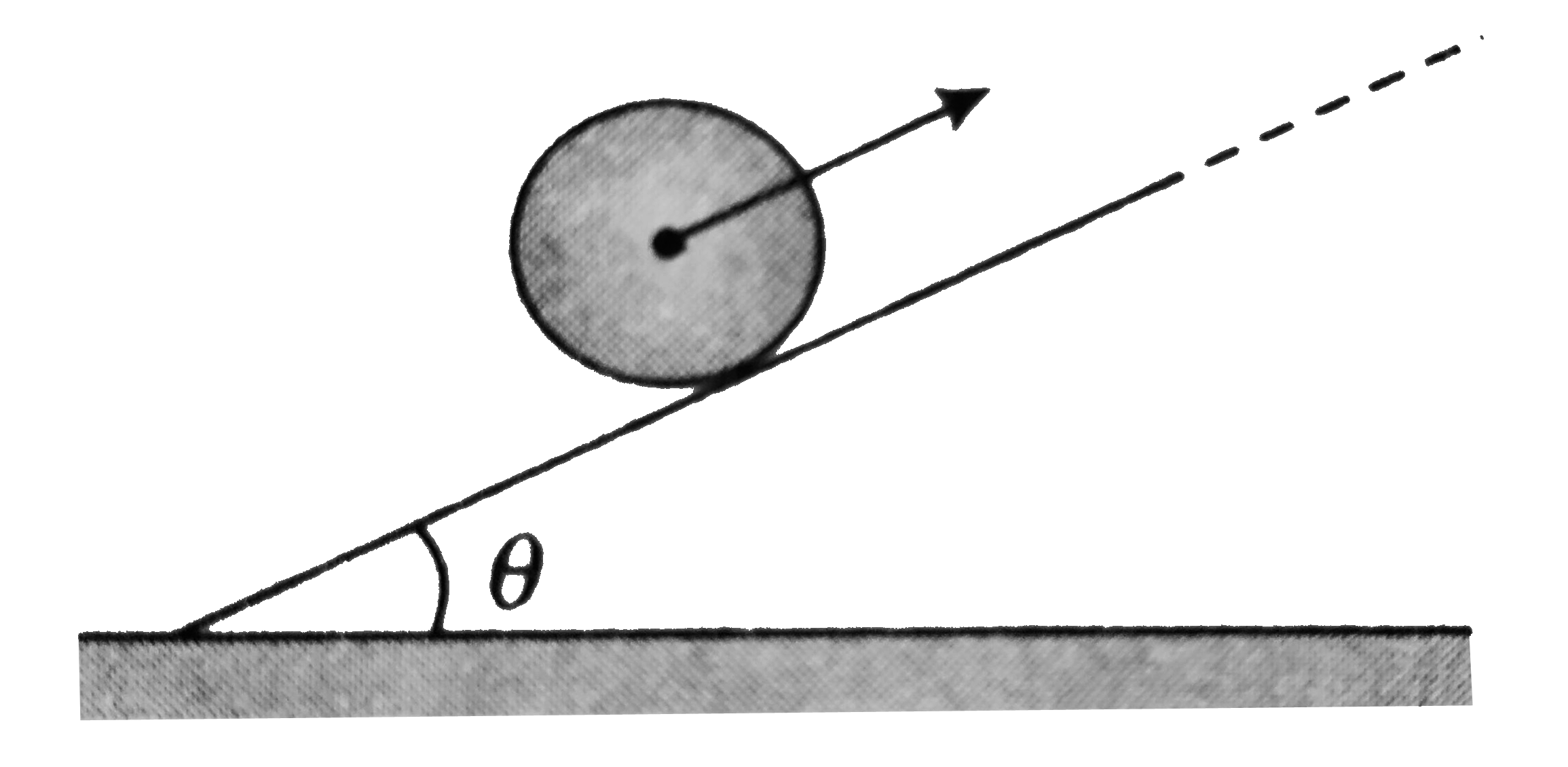
View SolutionA rolling object rolls without slipping down an inclined plane (angle of inclination `theta`), then the minimum acceleration it can have is.
 .
.
View SolutionSuppose you are standing on the edge of a spinning platform and step off at right angles to the edge (radially outward). Now consider it the other way. You are standing on the ground next to a spinning carousel and you step onto the platform at right angles to the edge (radially inward).
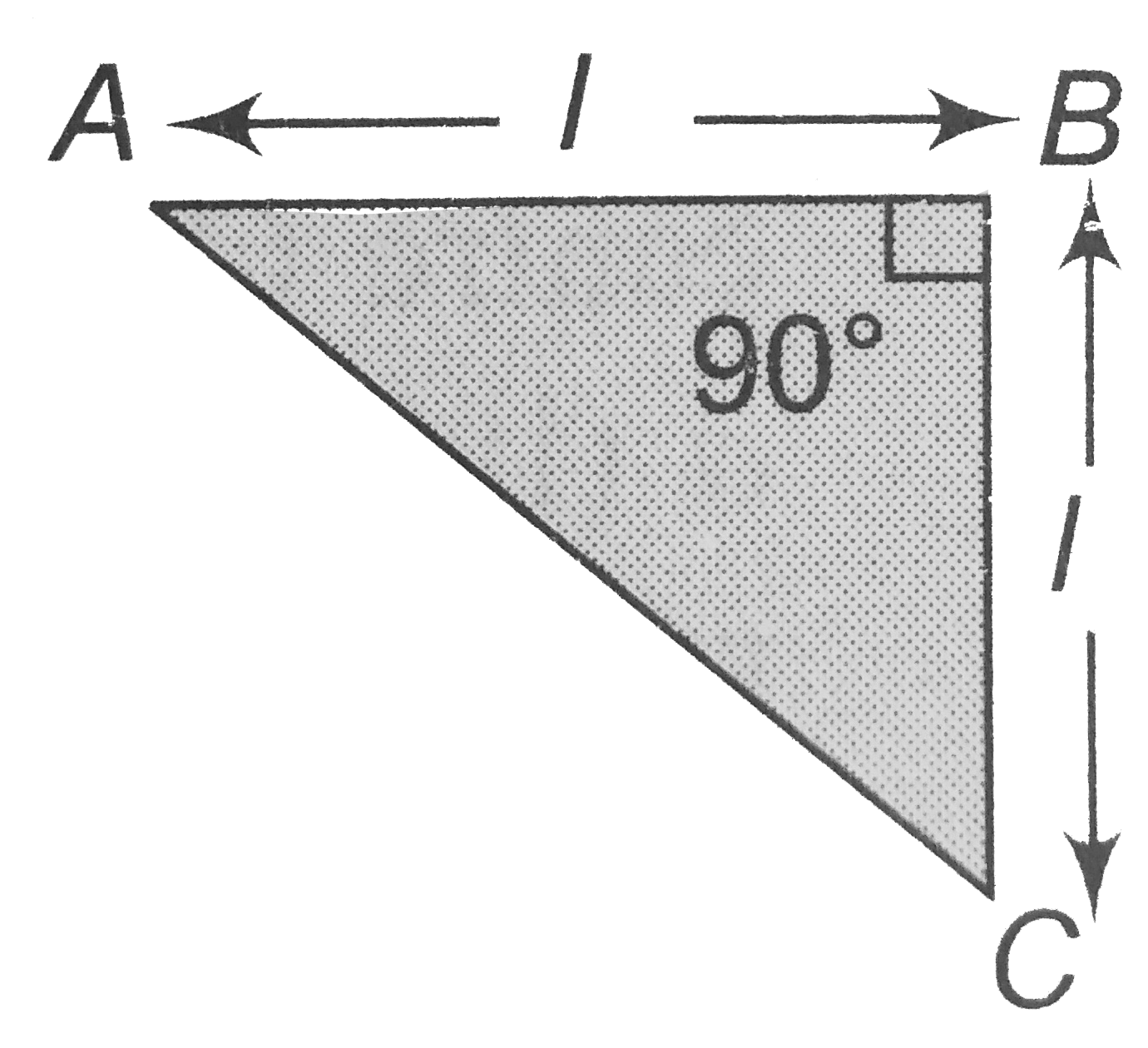
View SolutionFigure shows a thin metallic triangular sheet `ABC`. The mass of the sheet is `M`. The moment of inertia of the sheet about side `AC` is :
 .
.
View SolutionA sphere of mass `M` and radius `R` is moving on a rough fixed surface, having coefficient of friction `mu`. as shown in Fig. It will attain a minimum linear velocity after time `v_(0)gtomega_(0)R)`

View SolutionA uniform solid sphere rolls up (witout slipping) the fixed inclined plane, and then back down. Which is the correct graph of acceleration a of centre of mass of solid sphere as function of time `t` (for the duration sphere is on the incline)? Assume that the sphere rolling up has a positive velocity.
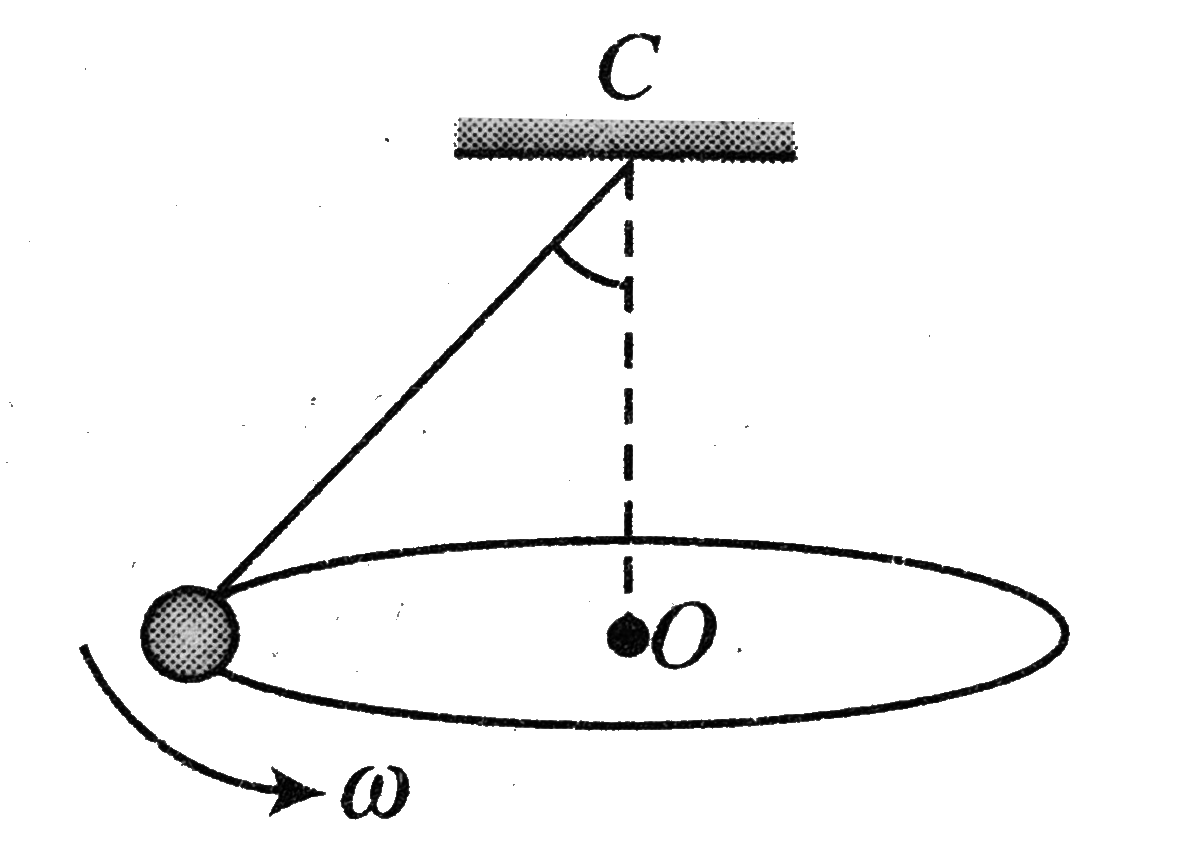
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. `C` is the pivot, `O` the centre of the circle in which the pendulum bob moves and `omega` the constant angular velocity of the bob. If `vecL` is the angular momentum about point `C`, then
View Solution
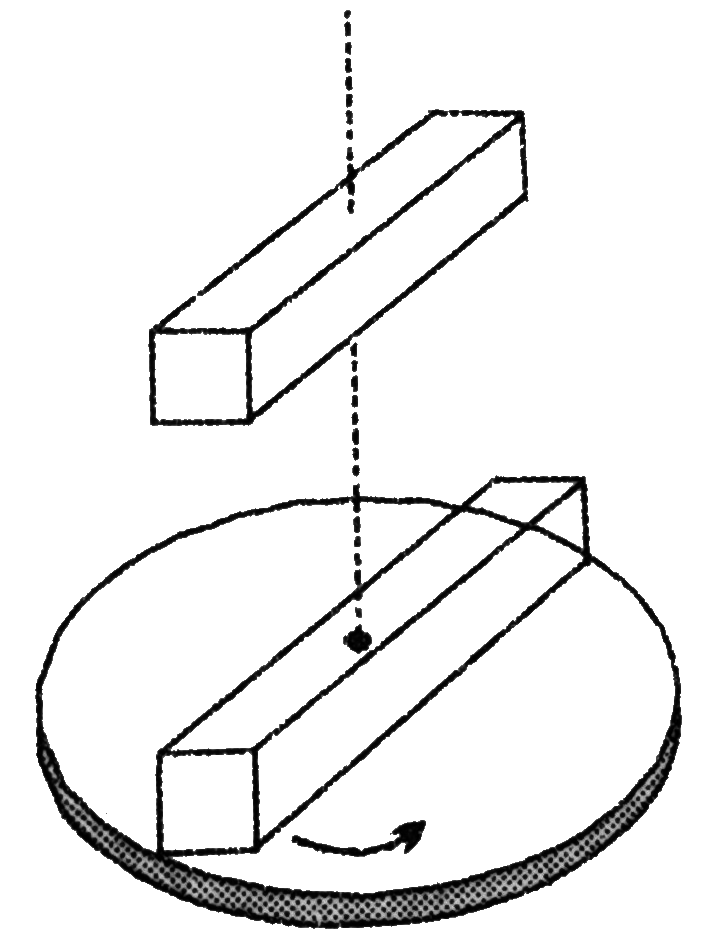
A child with mass `m` is standing at the edge of a merry go round having moment of inertia `I`, radius `R` and initial angular velocity `omega` as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity `v` with respect to the ground. The new angular velocity of the merry go round is
View SolutionTwo identical uniform solid spherical balls `A` and `B` of mass `m` each are placed on a the fixed wedge as shown in figure. Ball `B` is kept at rest and it is released just before two balls collides. Ball `A` rolls down without slipping on inclined plane and collide elastically with ball `B`. The kinetic energy of ball `A` just after the collision with ball `B` is:
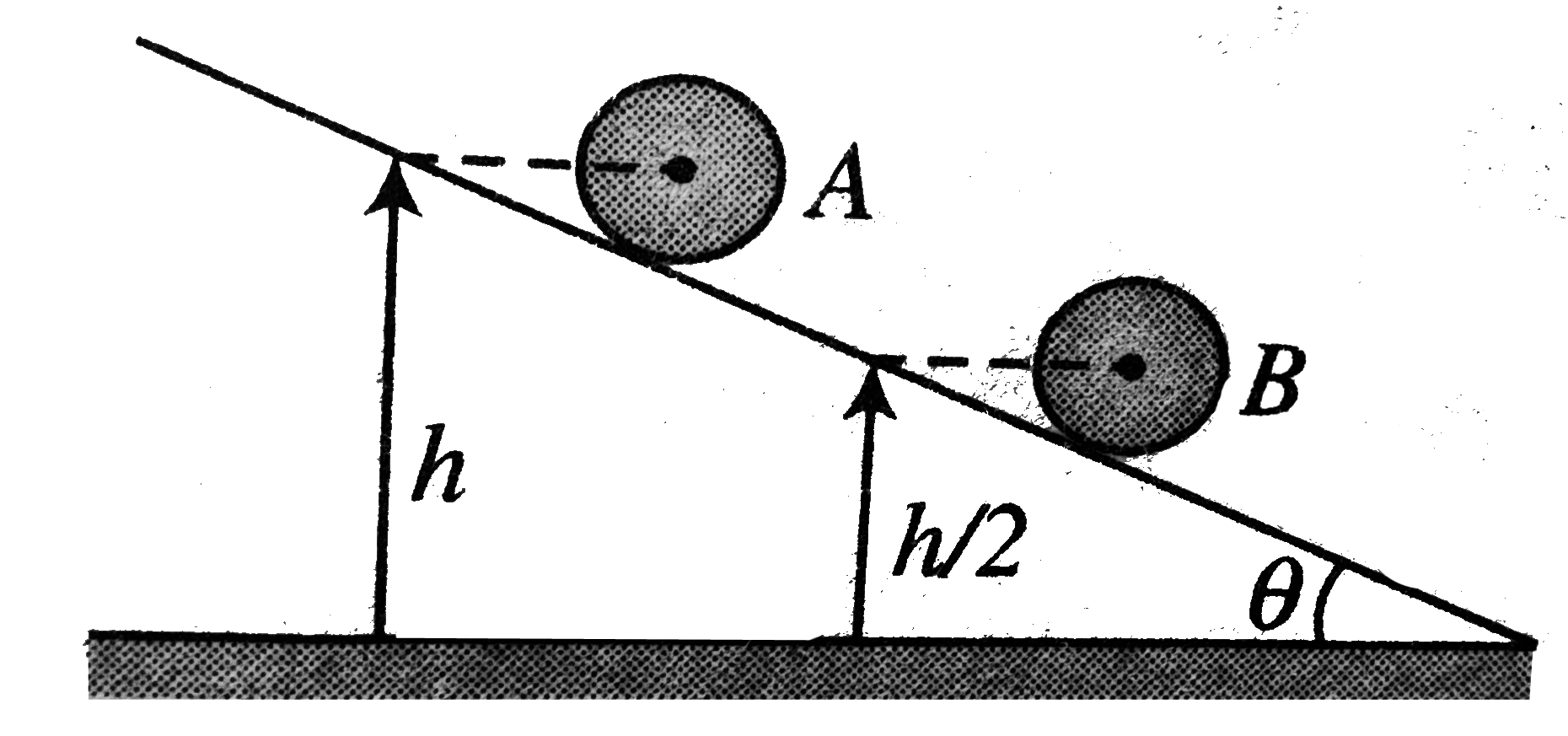
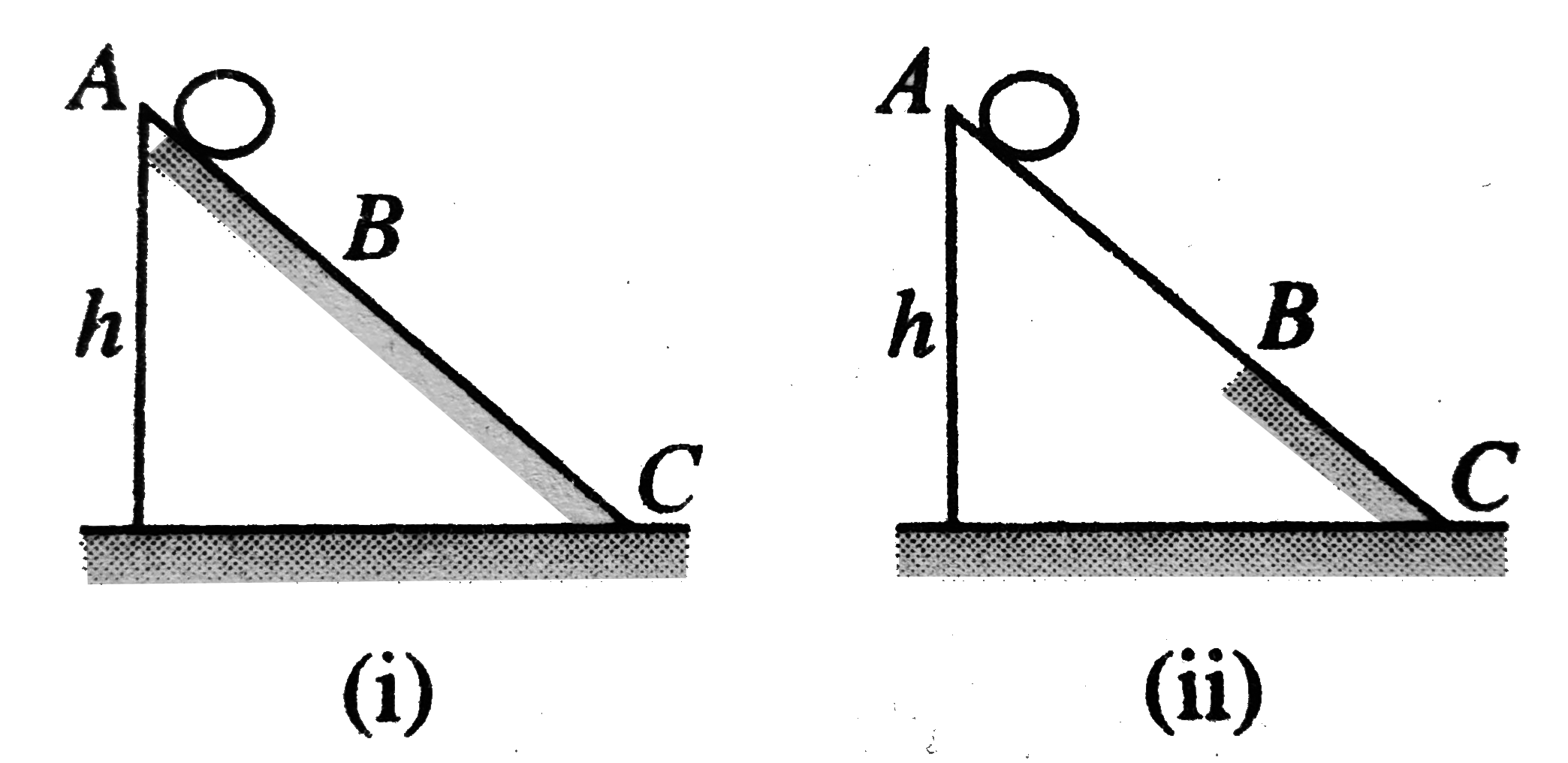
View SolutionIn both the figures all other factors are same, except that in figure (i) `AB` is rough and `BC` is smooth while in figure (ii) `AB` is smooth and `BC` is rough. In figure (i), if a sphere is released from rest it starts rolling. Now consider the figure (ii), if same sphere is A released from top of the inclined plane, what will be the kinetic energy of the sphere on reaching the bottom:
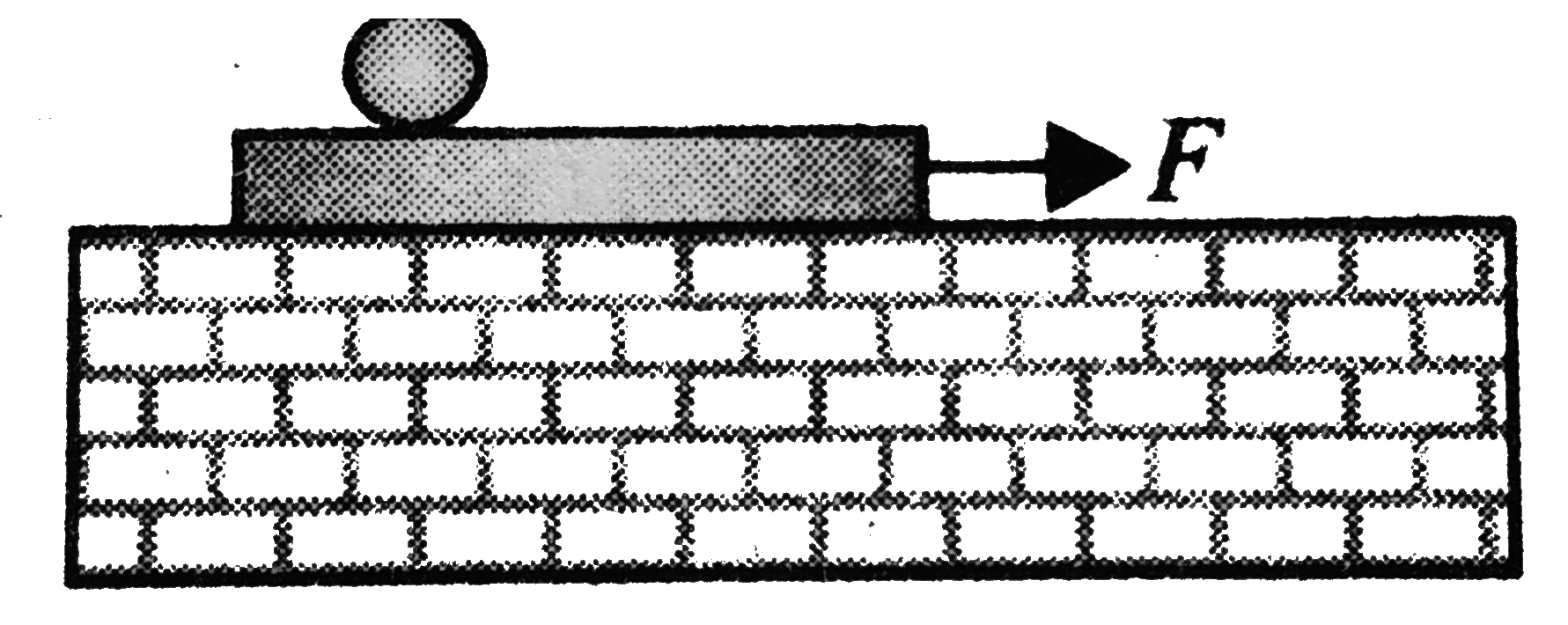
View SolutionA plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force `F`. If sphere does not slip over the plank. Which of the following is incorrect?
View SolutionA homogenous rod of length `l=etax` and mass `M` is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance `x` from the middle of the rod at a velocity `v_(0)` perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of `v_(0)`, then:
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View SolutionTwo uniform solid spheres having unequal rdii are released from rest from the same height on a rough incline. Ilf the spheres roll without slipping
View SolutionThree identical solid spheres move down three incline `A, B` and `C` are all of the same dimensions. A is without friction, the friction between `B` and a sphere is sufficient to cause rolling without slipping, the friction between `C` and a sphere causes rolling with slipping. The kinetic energies, of `A, B, C` at the bottom of the inclines are `E_(A),E_(B),E_(C)`.
View SolutionA rolling body is kept on a plank `B`. There is sufficient friction between `A` and `B` and no friction between `B` and the inclined plane. Then body:
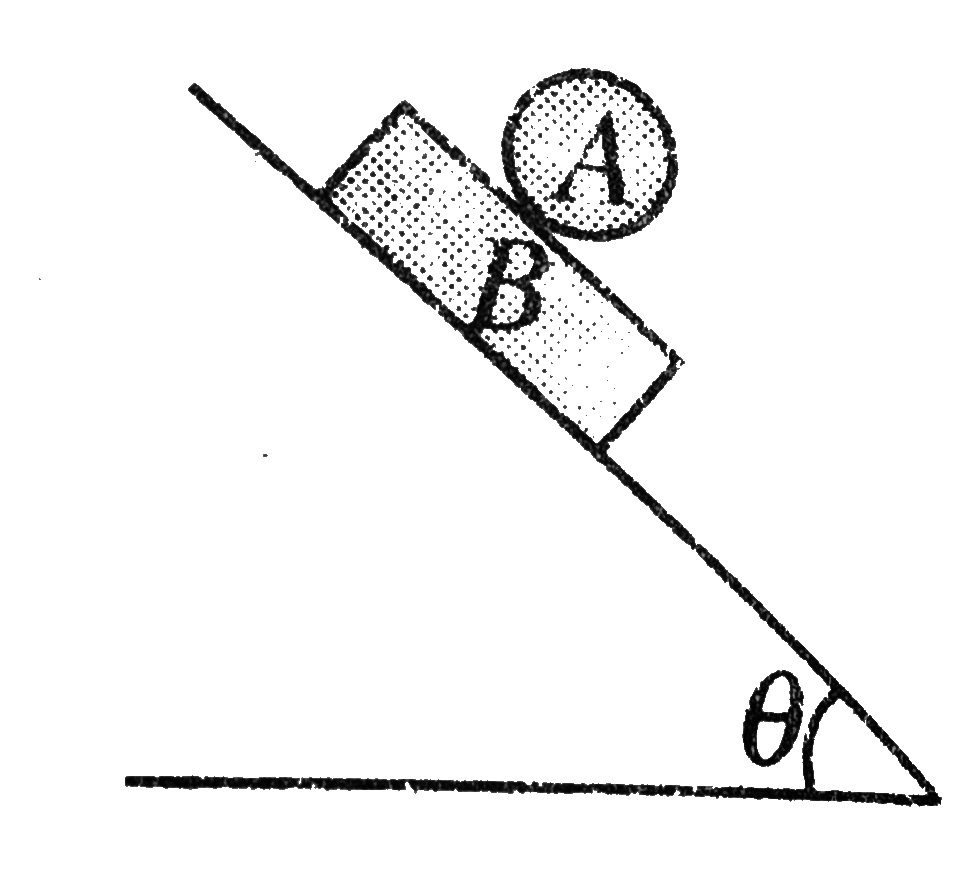
View SolutionA plank `P` is placed on a solid cylinder `S`, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of `P` to the kinetic energy of `S` is:

View SolutionA fly wheel rotating about a fixed axis has a kinetic energy of `360 J`. When its angular speed is `30 rad s^(-1)`. The moment of inertia of the wheel about the axis of rotation is
View SolutionFigure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then
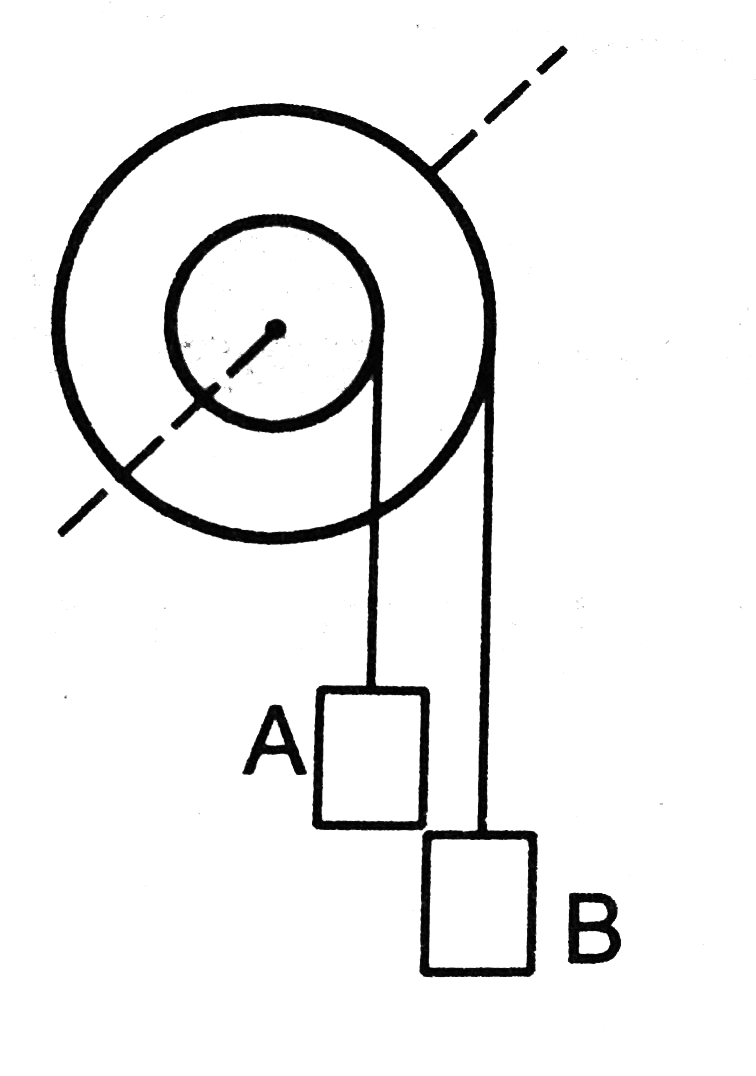
View SolutionA body is rolling without slipping on a horizontal plane. The rotational energy of the body is `40% `of the total kinetic energy. Identify the body.
View SolutionA certain bicycle can go up a gentle incline with constant speed when the frictional force of ground pushing the rear wheel is `F_(2) = 4 N`. With what force `F_(1)` must the chain pull on the sprocket wheel if `R_(1) = 5m` and `R_(2) = 30m`?
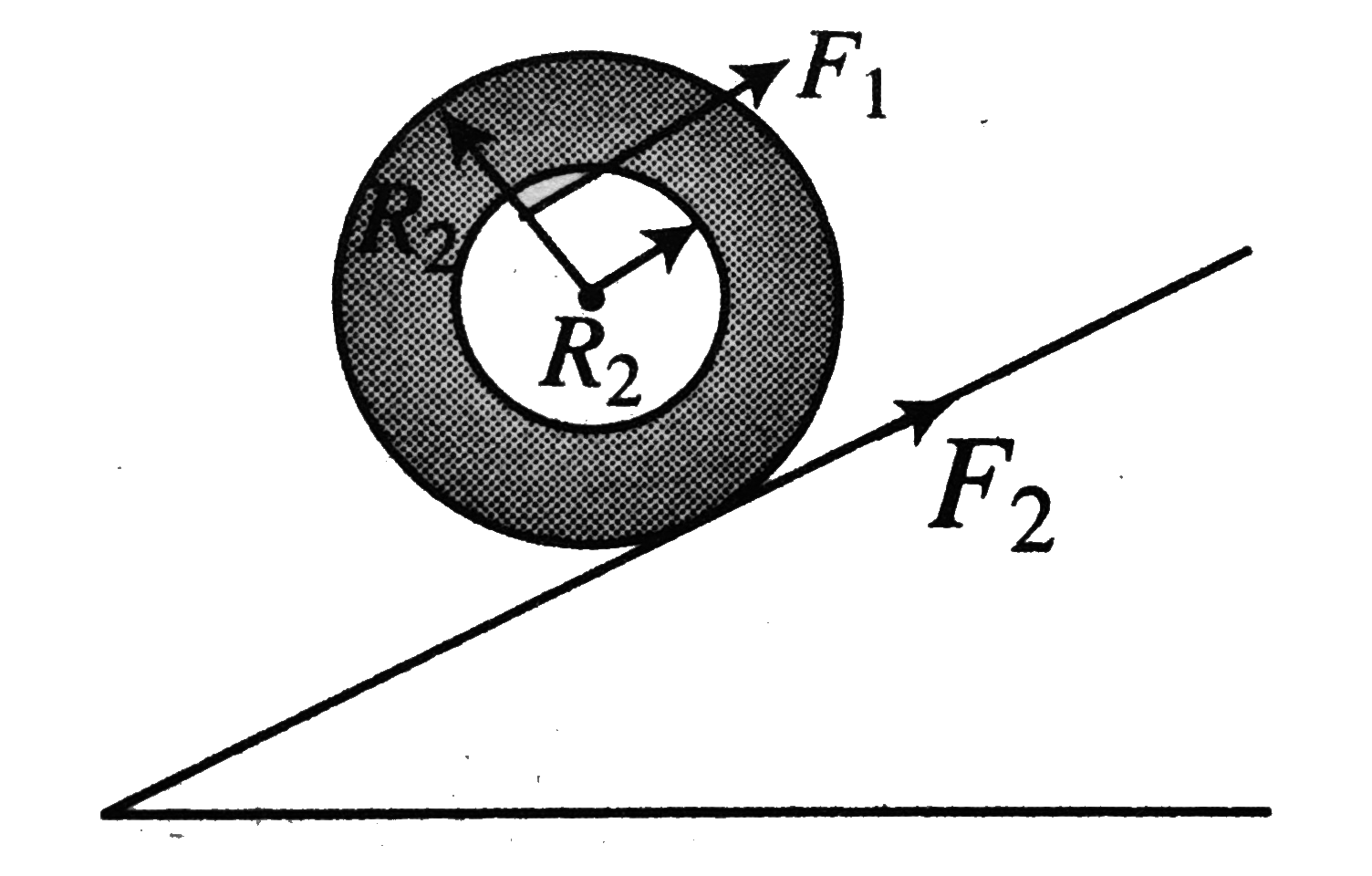
View SolutionA small stone of mass `m` is attached to a light string which passes through a hollow tube. The tube is held by one hand and the free end of the string by the other hand. The mass is set into revolution in a horizontal circle of radius `r_(1)` with a speed `v_(1)` . The string is pulled down shortening the radius of the circular path to `r_(2)`. Which of the following is not correct? (`omega_(1)` and `T` have usual meanings)
View SolutionA loop and a disc have same mass and roll without slipping with the same linear velocity `v`. If the total kinetic energy of the loop is `8 J`, the kinetic energy of the disc must be.
View SolutionAverage torque on a projectile of mass `m` (initial speed `u` and angle of projection `theta`) between initial and final positions `P` and `Q` as shown in figure, about the point of projection is :
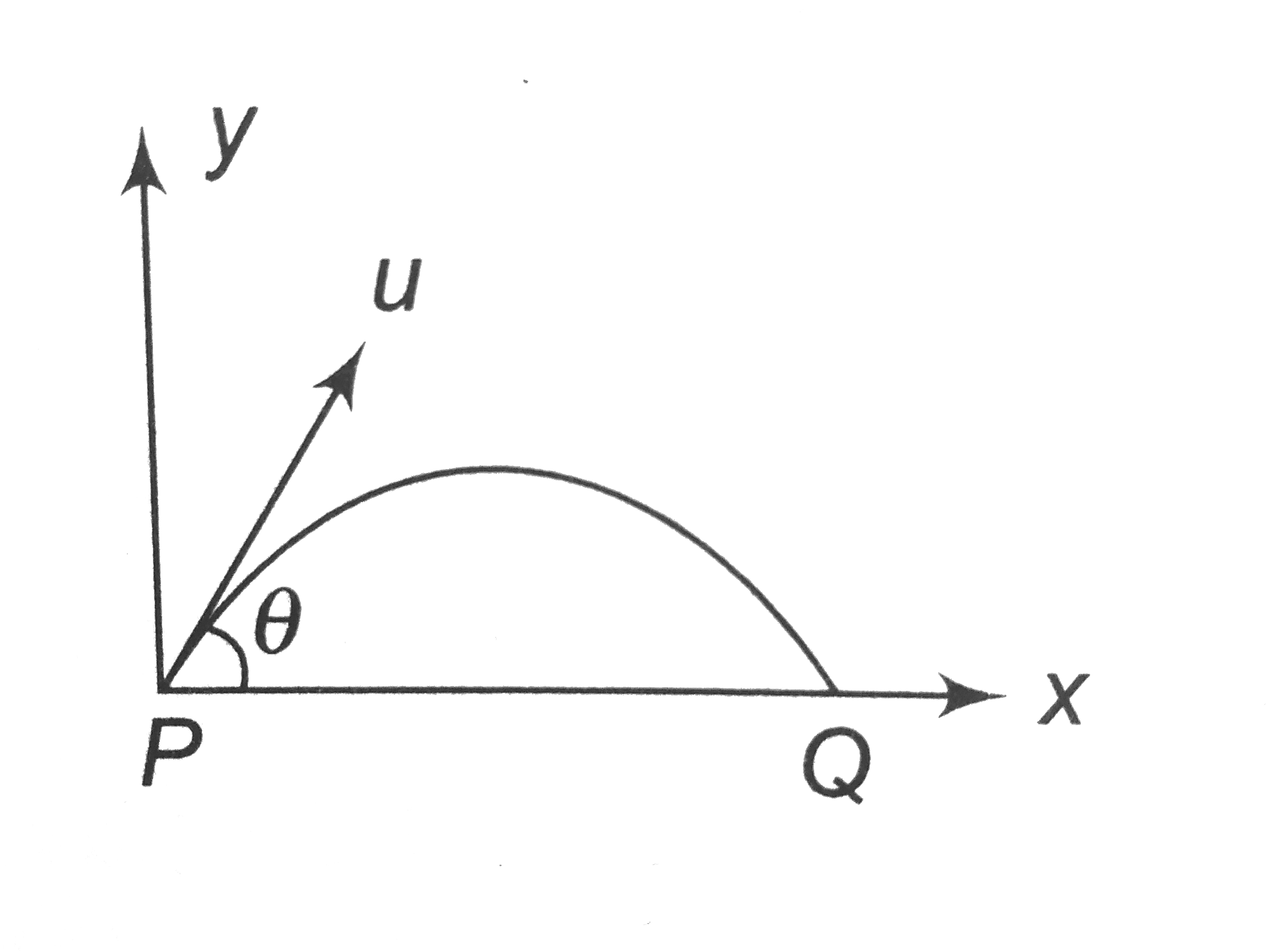 .
.
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity `omega_(0)`. Once the pure rolling starts let `v_(1)` and `v_(2)` be the linear speeds of their centres of mass. Then
View SolutionTwo cylinders having radii `2R` and `R` and moment of inertia `4I` and `I` about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity `omega_(0)`. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
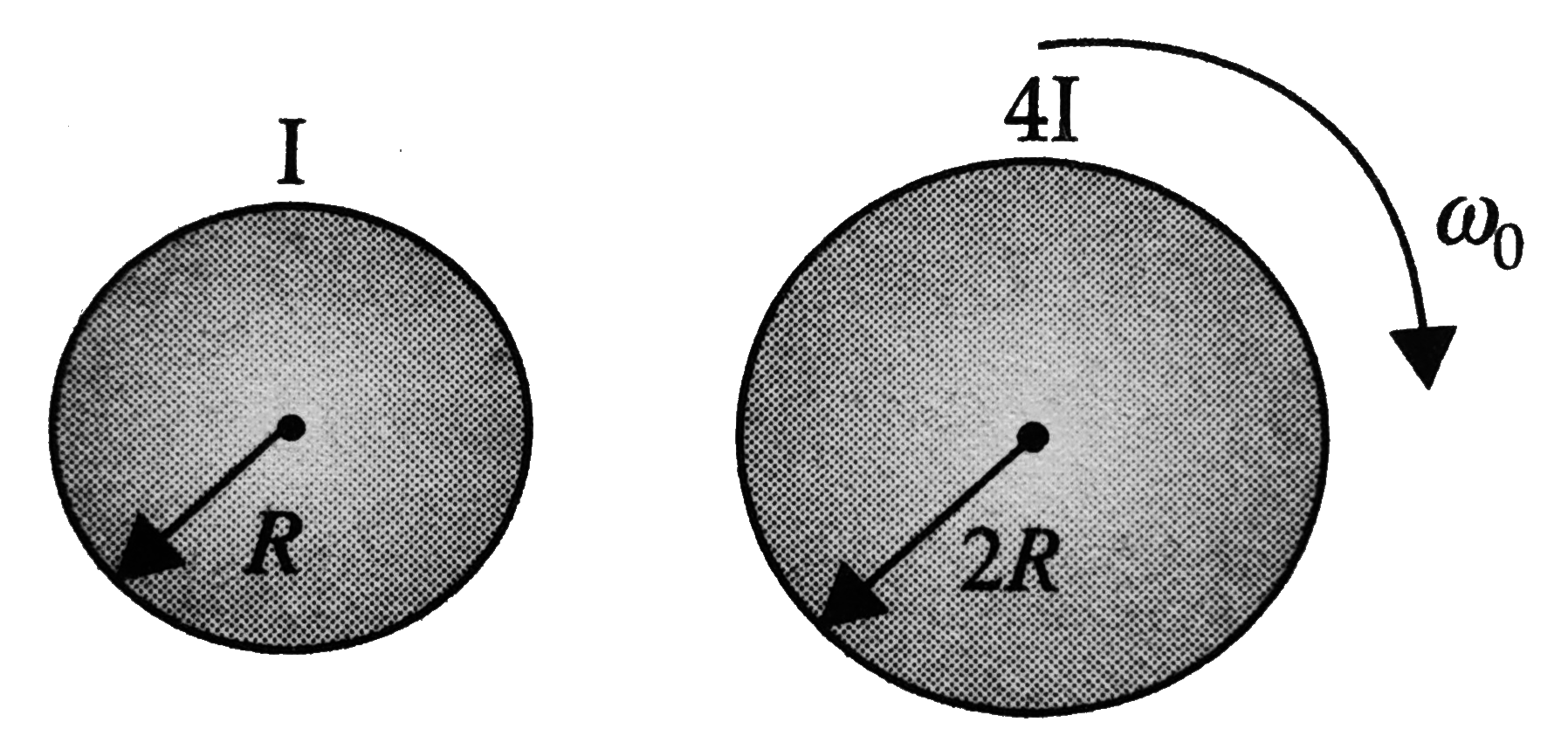
View SolutionPortion `AB` of the wedge shown in figure is rough and `BC` is smooth. A solid cylinder rolld without slipping from `A` to `B`. Find the ratio of translational kinetic energy to rotationa linetic energy, when the cylinder reaches point `C`.
 .
.
View SolutionIn the figure shown mass of both, the spherical body and block is `m`. Moment of inertia of the spherical body about centre of mass is `2mR^(2)`. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
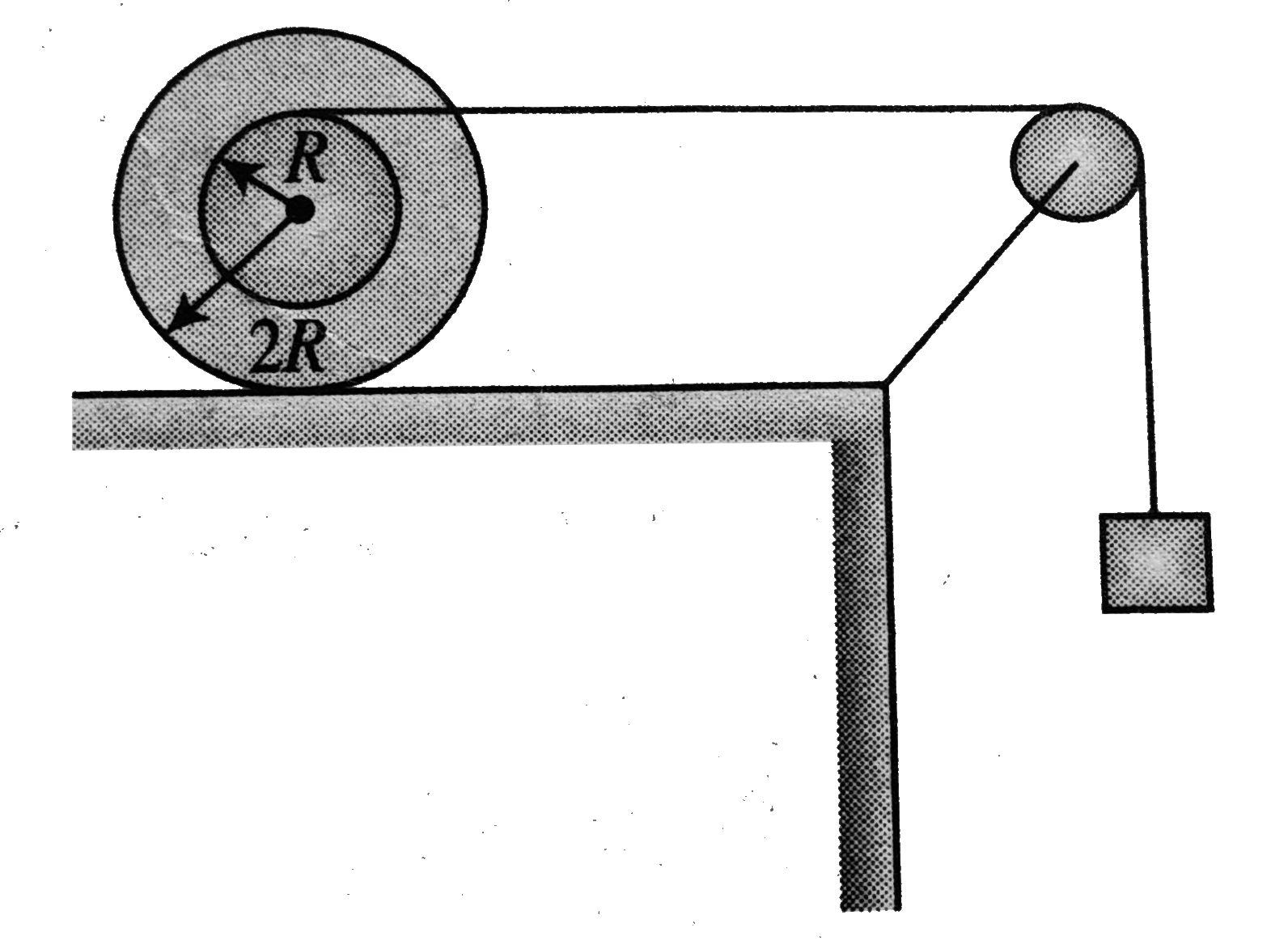
View SolutionA cylinder executes pure rolling without slipping with a constant velocity on a plank, whose upper surface is rough enough, but lower surface is smooth. The plank is kept at rest on a smooth horizontal surface by the application of an external force `F`. Choose the correct alternative:
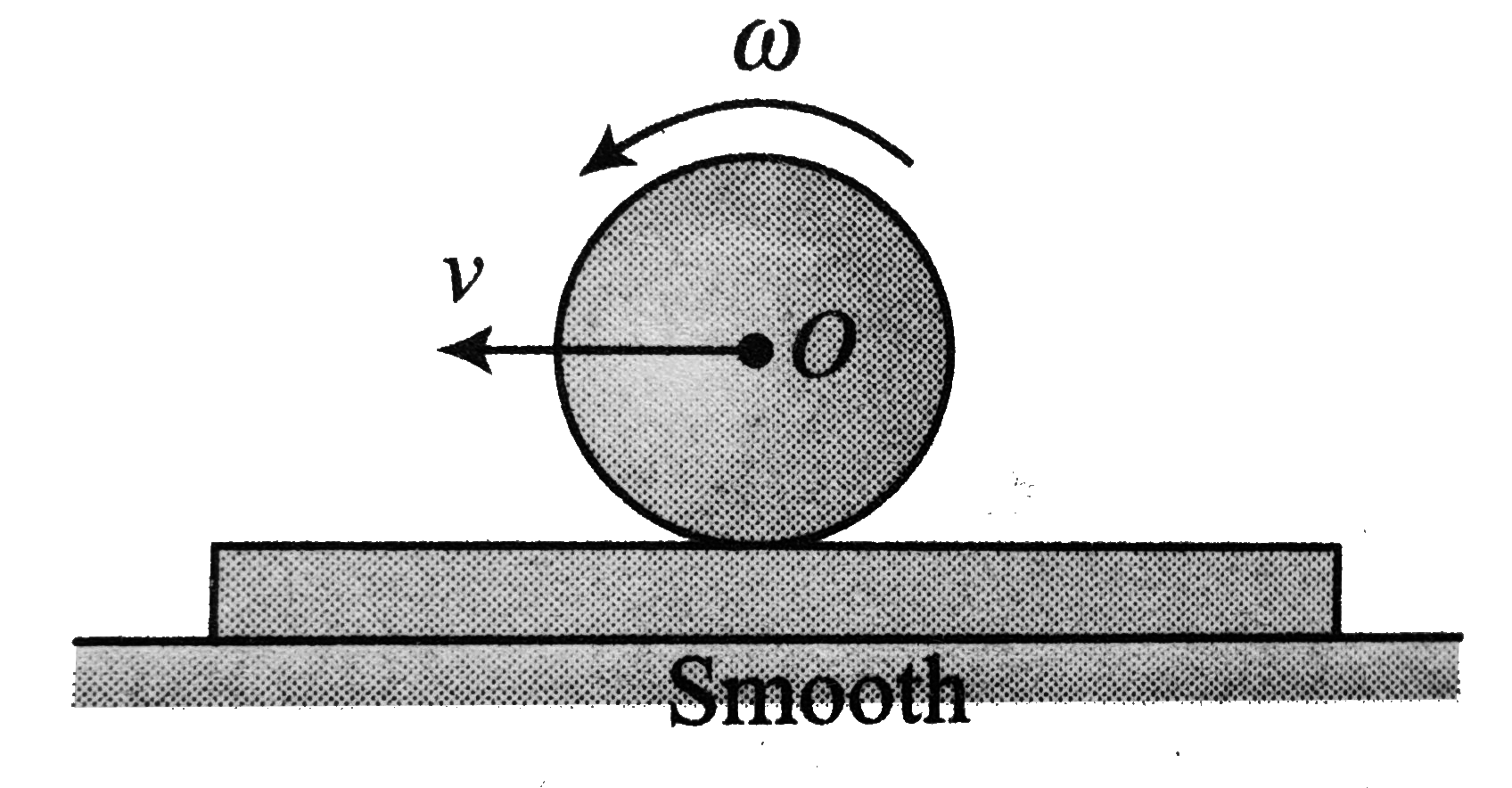
View SolutionA solid sphere rolls down two different inclined planes of the same height but of different inclinations
View SolutionA body of mass `m` slides down an smooth incline and reaches the bottom with a velocity, Now smooth incline surface is made rough and the same mass was in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been:
View SolutionTwo rigid bodies `A` and `B` rotate with angular momenta `L_(A)` and `L_(B)` respectively. The moments of inertia of `A` and `B` about the axes of rotation are `I_(A)` and `I_(B)` respectively. If `I_(A)=I_(B)//4` and `L_(A)=5L_(B)`, then the ratio of rotational kinetic energy `K_(A)` of `A` to the rotational kinetic energy `K_(B)` of `B` is given by
View SolutionTwo discs, each having moment of inertia `5 kg m^(2)`. about its central axis, rotating with speeds `10 rad s^(-1)` and `20 rad s^(-1)`, are brought in contact face to face with their axes of rotation coincided. The loss of kinetic energy in the process is
View Solution
Single Correct questions and complete solutions for chapter RIGID BODY DYNAMICS 2 of CENGAGE PHYSICS (HINGLISH) of Class 11