Complete Solutions to Exercise 3.4 of chapter RIGID BODY DYNAMICS 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Exercise 3.4 |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
View SolutionA uniform bar of length `6a` and mass `8m` lies on a smooth horizontal table. Two point masses `m` and `2m` moving in the same horizontal plane with speeds `2v` and `v` respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
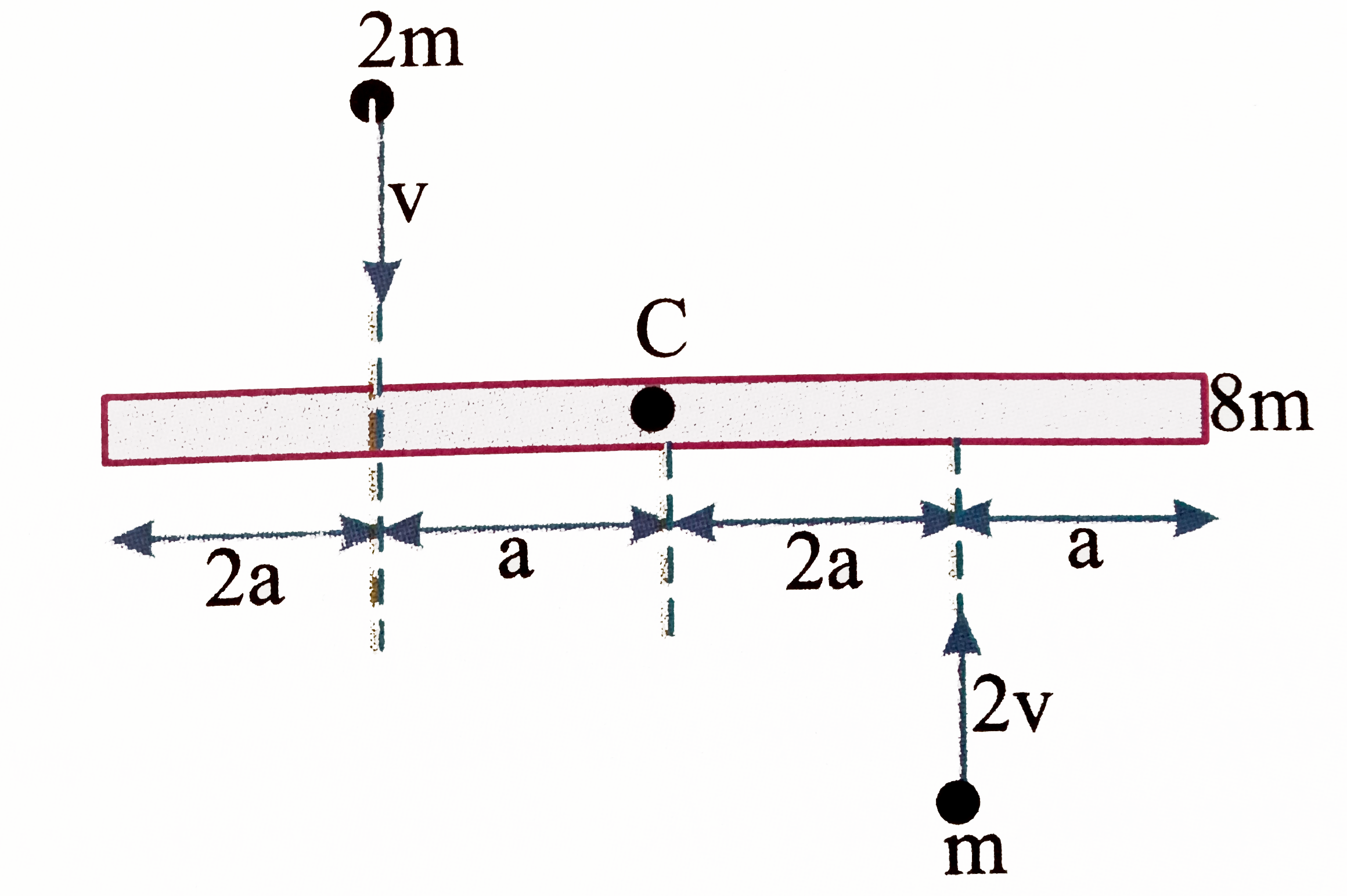
View SolutionA circular wooden hoop of mass `m` and radius `R` rests fiat on a frictionless surface. A bullet, also of mass `m` and moving with a velocity `v`, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than `R`. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
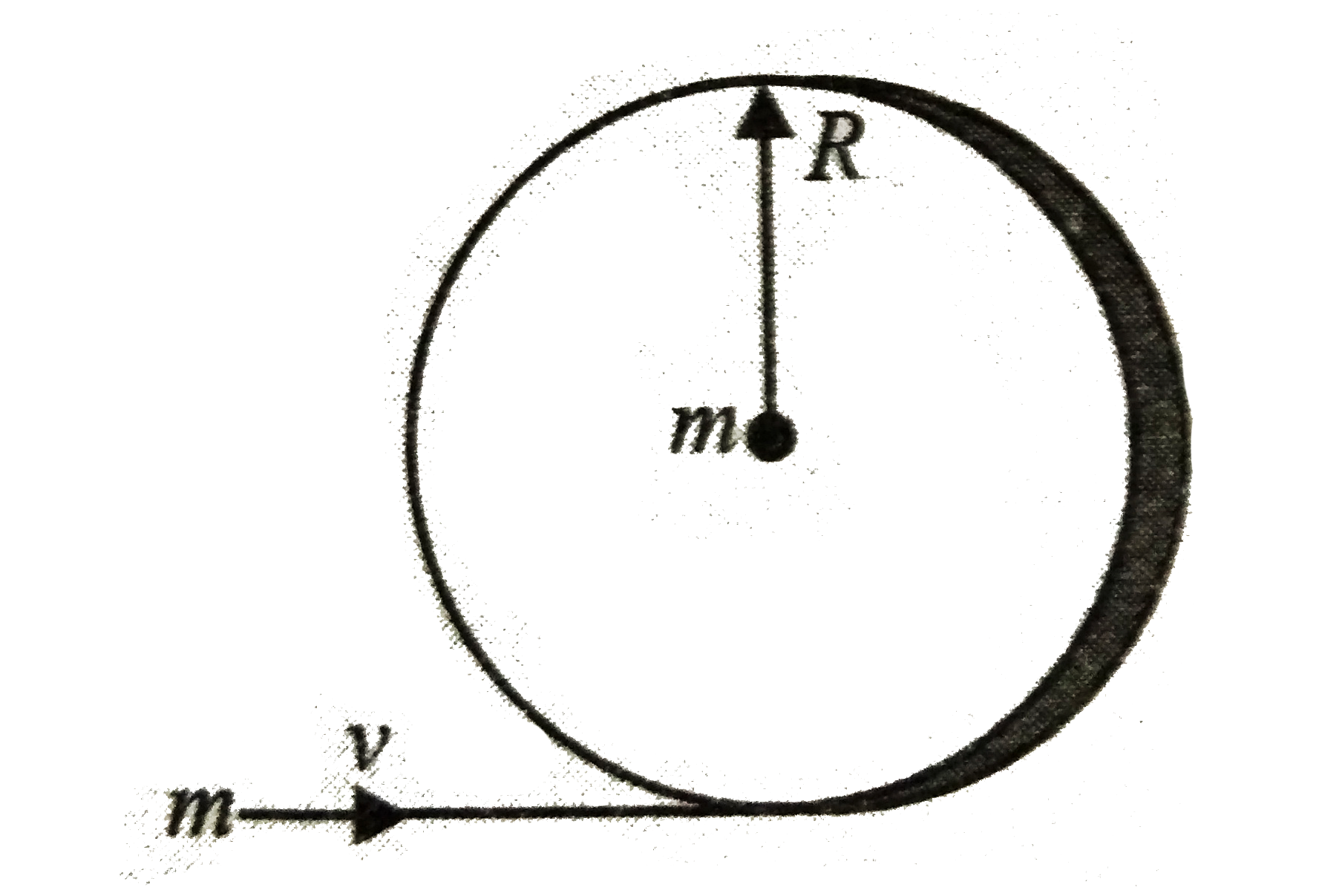
View Solution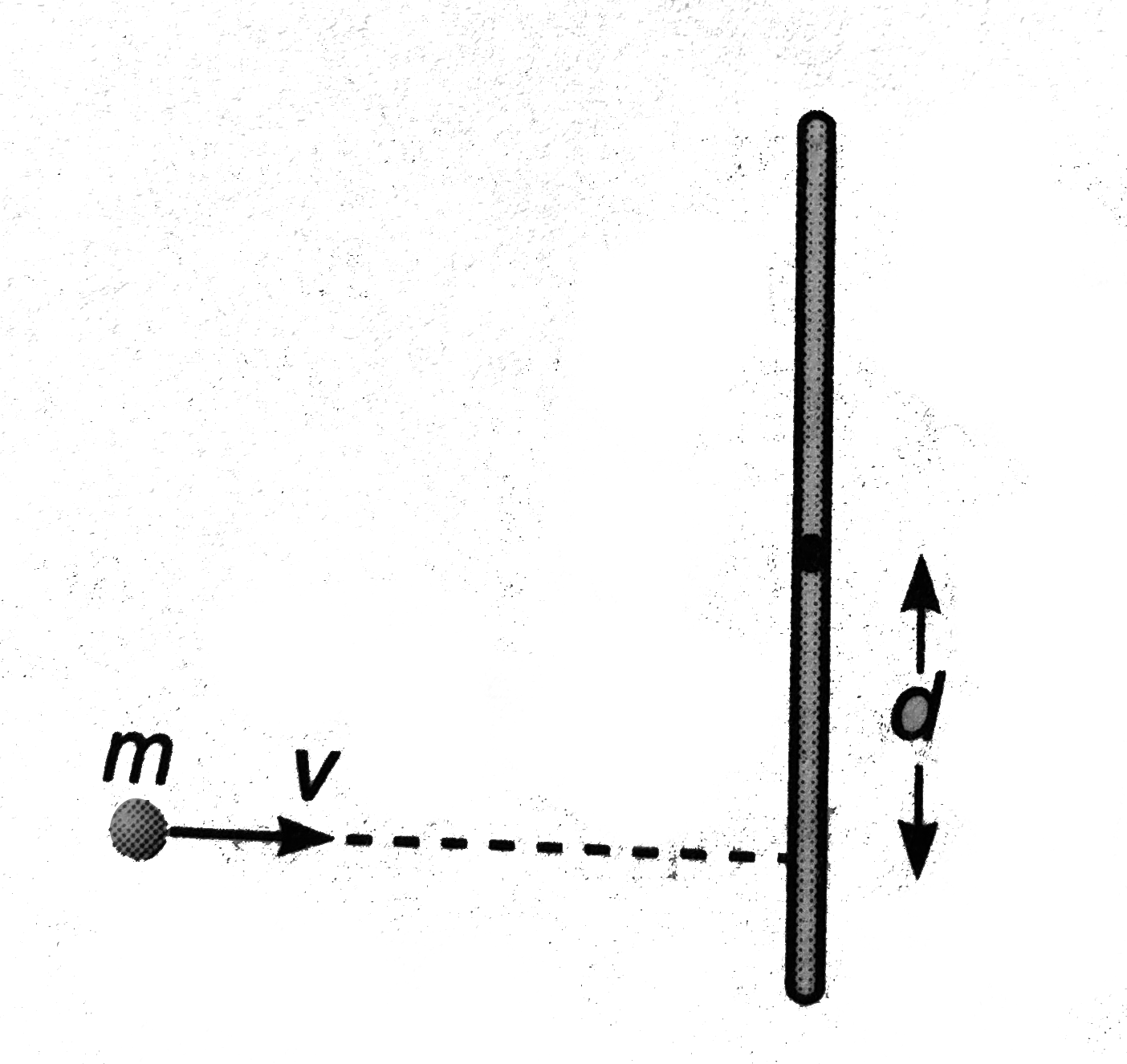
A stick of length `l` lies on horizontal table. It has a mass `M` and is free to move in any way on the table. A ball of mass `m` moving perpendicularly to the stick at a distance d from its centre with speed `v` collides elastically with it as shown in figure. What quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?
View SolutionA thin uniform rod of length `l` is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.
View SolutionA thin spherical shell of radius `R` lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
View SolutionA wheel rolling along a rough horizontal surface with an angular velocity `omega` strikes a rough vertical wall, normally. Find the initial angular velocity, as it tends to roll up the wall (neglect any slippage) due to impulse.
View SolutionTwo identical particles `B` and `C` each of mass `50 g` are connected by a light rod of length `30 CM`. Another particle `A` of same mass moving With a speed `u = 60 CM//s` strikes `B`, in a direction perpendicular to `AB`, and sticks to it. The whole process takes place on a smooth horizontal plane. Find the angular velocity `omega` of the system about its centre of mass, immediately after the impact.

View SolutionA rod `AB` of mass `M` and length `8l` lies on a smooth horizontal surface. A particle, of `A` mass `m` and velocity `v_(0)` strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of `v_(0)//8` and the particle rebounds back with a (not to scale) speed of `v_(0)//4`. Find the following: a. The ratio `M//m`. b. The angular velocity of the rod about `O`. c. The coefficient of restitution `'e'` for the collision. d. The velocities of the ends `'A'` and `'B'` of the rod, namely, `v_(A)` and `v_(B)` respectively.
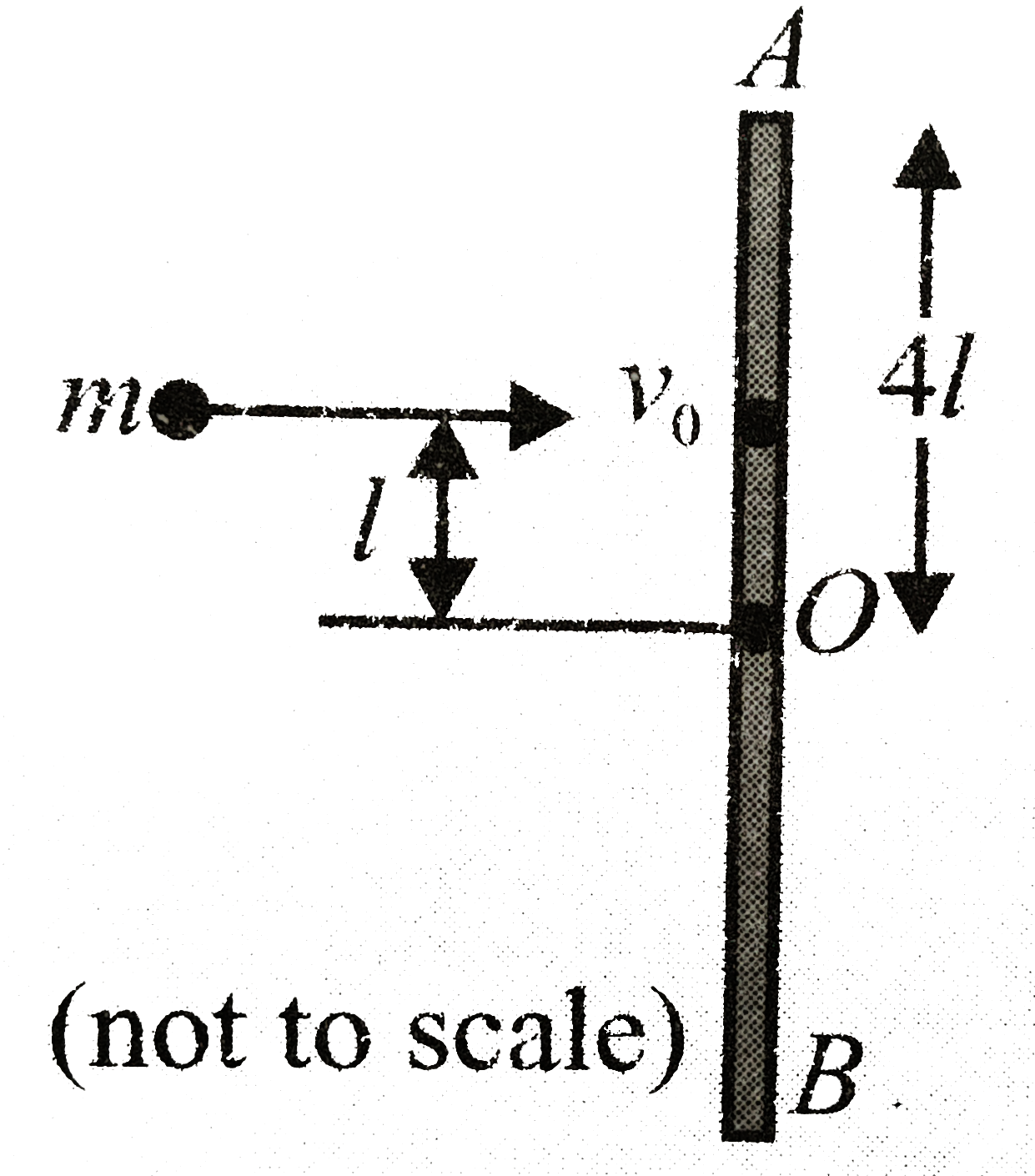
View SolutionA uniform rod of mass M and length `a` lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance `a/4` from the centre and stops after the collision. Find (a). the velocity of the centre of the rod and (b). the angular velocity of the rod abut its centre just after the collision.
View SolutionIn the shown figure a mass `m` slides down the frictionless surface from height `h` and collides with the uniform vertical rod of length `L` and mass `M` after collision the mass `m` sticks to the rod. The rod is face to rotate in a vertical plane about fixed axis through `O`. Find the maximum angular deflection of the rod from its initial position.

View SolutionA small mass particle is projected with an initial velocity `v_(0)` tangent to the horizontal rim of smooth hemispherical bowl at a radius `r_(0)` from the vertical centre line, as shown at point A. As the particle slide past point `B`, a distance `h` below `A` and distance `r` from the vertical centre line, its velocity `v` makes an angle `theta` with the horizontal tangent to the bowl through `B`. Determine `theta`.

View SolutionA thin uniform rod of length `l` is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.
View Solution
Exercise 3.4 questions and complete solutions for chapter RIGID BODY DYNAMICS 2 of CENGAGE PHYSICS (HINGLISH) of Class 11