Complete Solutions to Exercise 3.3 of chapter RIGID BODY DYNAMICS 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Exercise 3.3 |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Figure (a) and (b) shows two different arrangements of a spool being pulled with a constant force `F` in each case. Identify the direction of motion of the centre of mass, and the direction of friction force in each case.

a. The `CM` moves along……………….`x`-axis .
b. The friction force acts along…………………. `x`-axis.
c. The `CM` moves along .....`x`-axis.
d. The friction force acts along…………….. `x`-axis.
View SolutionA sphere moving with a velocity `v_(0)` on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
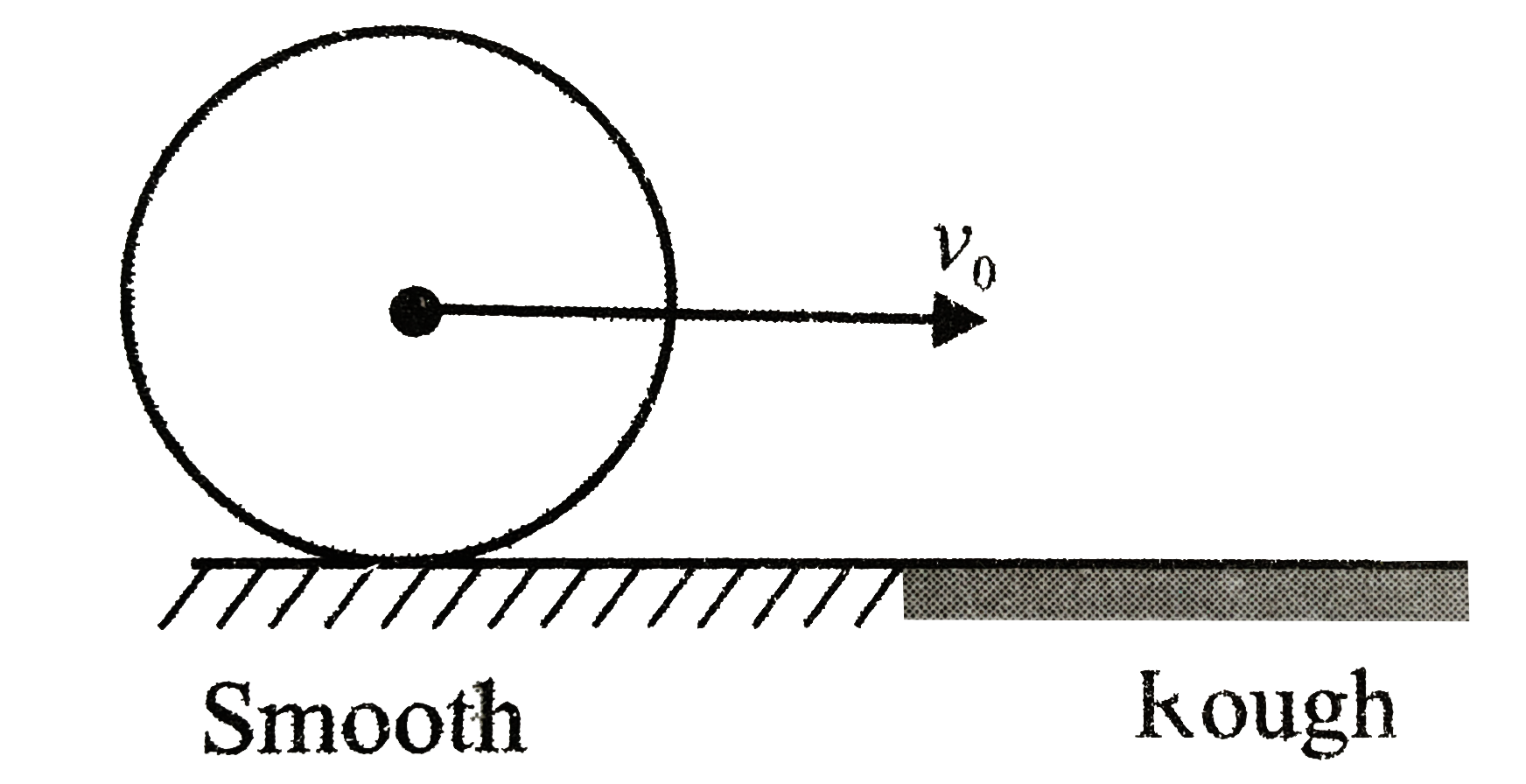
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point `OD` the surface is conserved.
d. The final velocity attained by the centre of mass is `2v_(0)//3`.
View SolutionA cylinder of mass at and radius `R` rolls on a stationary plank of mass `M`. The lower surface of the plank is smooth and the upper surface is sufficiently rough with a coefficient of friction `mu`. A man is to hold the plank stationary with respect to the ground, as shown Fig.
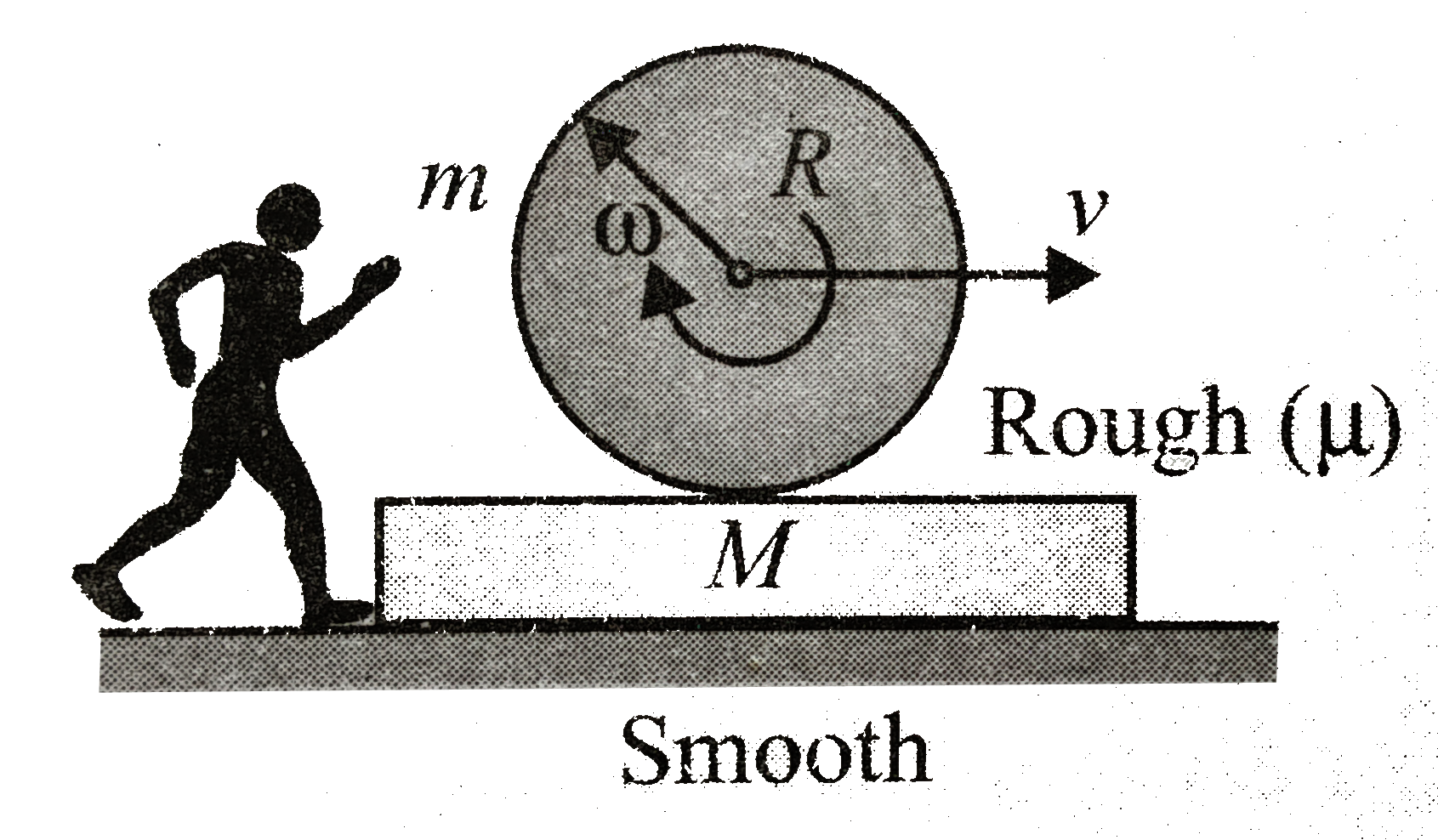
The force exerted by the man to keep the plank stationary is equal to……
View SolutionCalculate the kinetic energy of a tractor crawler belt of mass `m` if the tractor moves with a velocity `v`. There is no slipping. Neglect the size of the wheels.

View SolutionA constant horizontal force of `10 N` is applied at the centre of a wheel of mass `10 kg` and radius `0.30 m`. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is `0.60 m//s^(2)`.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View SolutionA uniform solid cylinder of mass `m` rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force `F`.
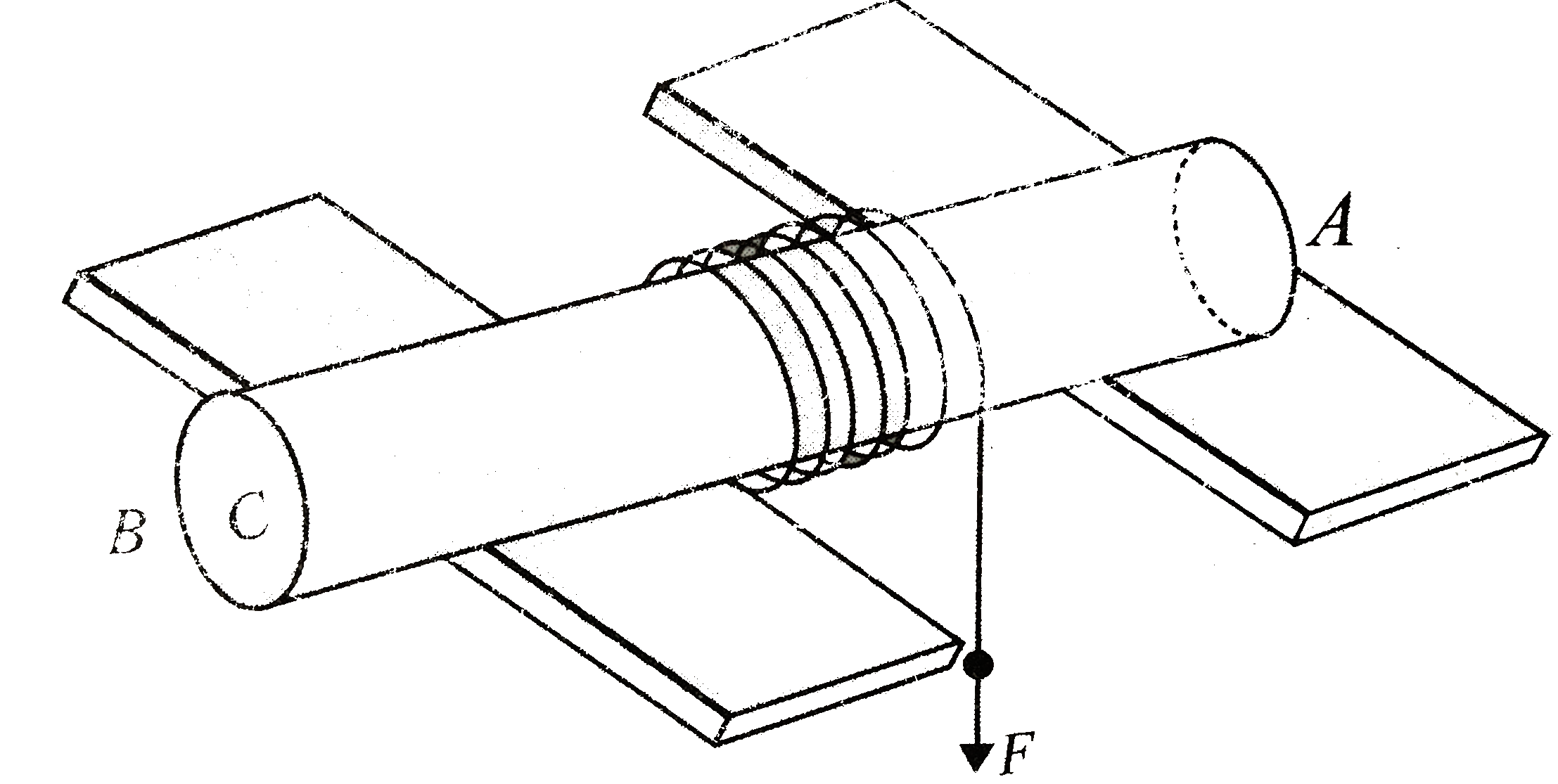
Find the maximum magnitude of the force `F` which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to `mu`. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA load of mass `m` is attached to the end of a string wound on a cylinder of mass `M` and radius `R`. The string passes round a pulley.
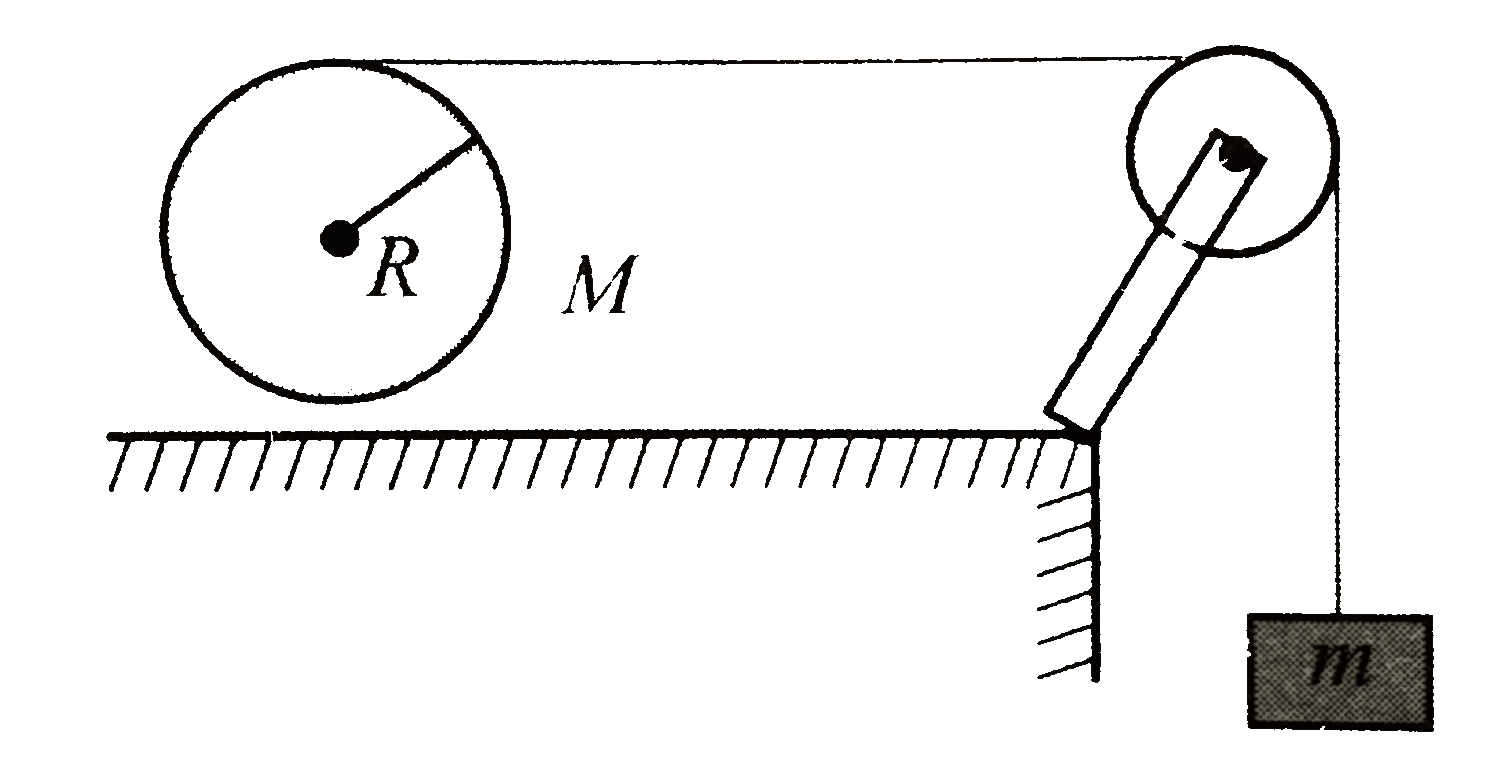
a. Find the acceleration of the cylinder `M` when it rolls.
b. If the coefficient of friction is `mu`. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View SolutionFind the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (`Take M = 4m` and `g =10 m//s^(2)`)
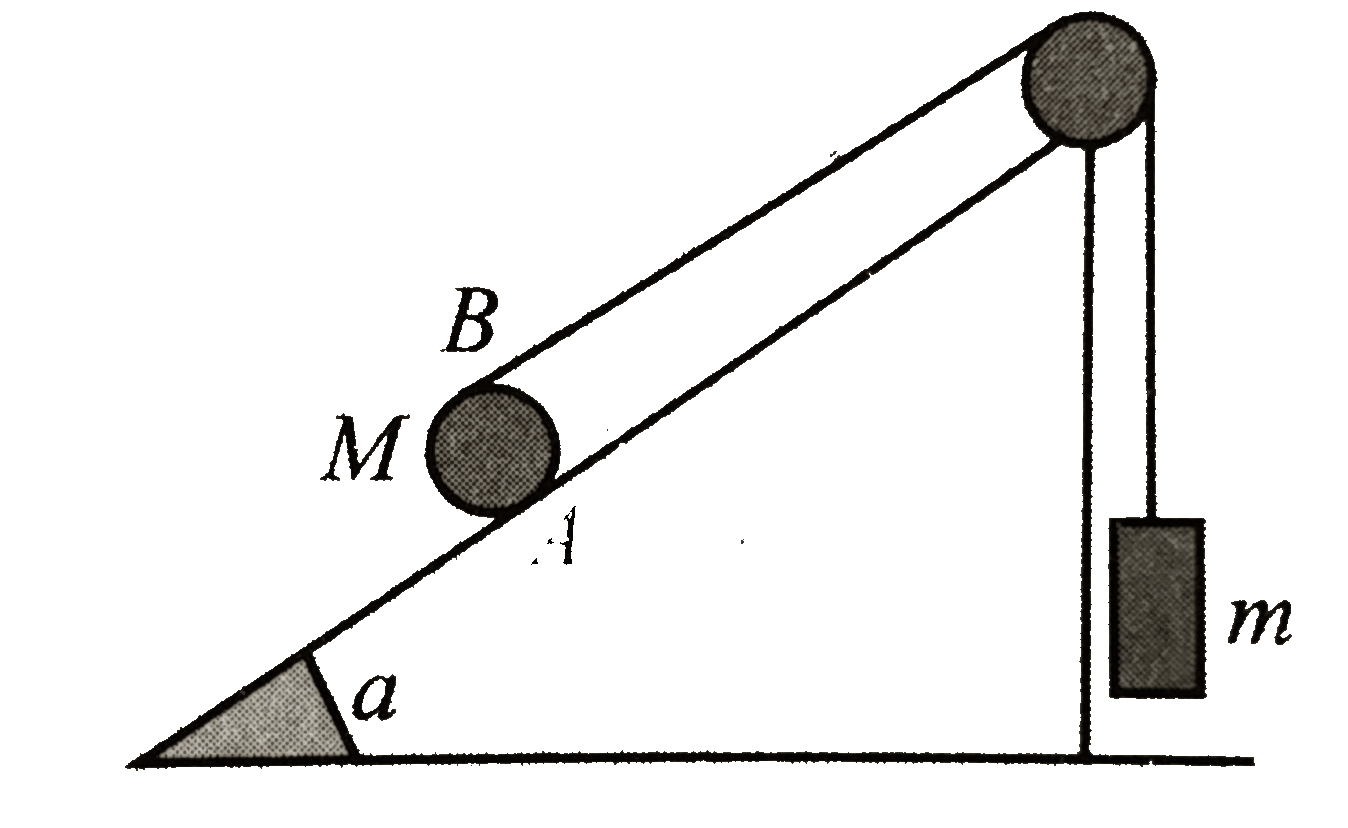
View SolutionA spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass `m` is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is `M` and radius is `R`. Find the acceleration of the falling mass `m`. Neglect the mass of the connecting tube and slipping of the spool.

View SolutionA solid cylinder wheel of mass `M` and radius `R` is pulled by a force `F` applied to the centre of the wheel at `37^@` to the horizontal. If the wheel is to roll without slipping, what is the maximum value of `|F|` ? The coefficients of static and kinetic friction are `mu_(s)=0.40` and `m_(k)=0.30. (sin37^@=3/5)`
View SolutionFind the acceleration of a system consisting of a cylinder of mass `m` and radius `R` and a plank of mass `M` placed an a smooth surface if it is pulled with a force `F` as shown Fig. Given that sufficient friction is present between the cylinder and the plank surface to prevent sliding of the cylinder.

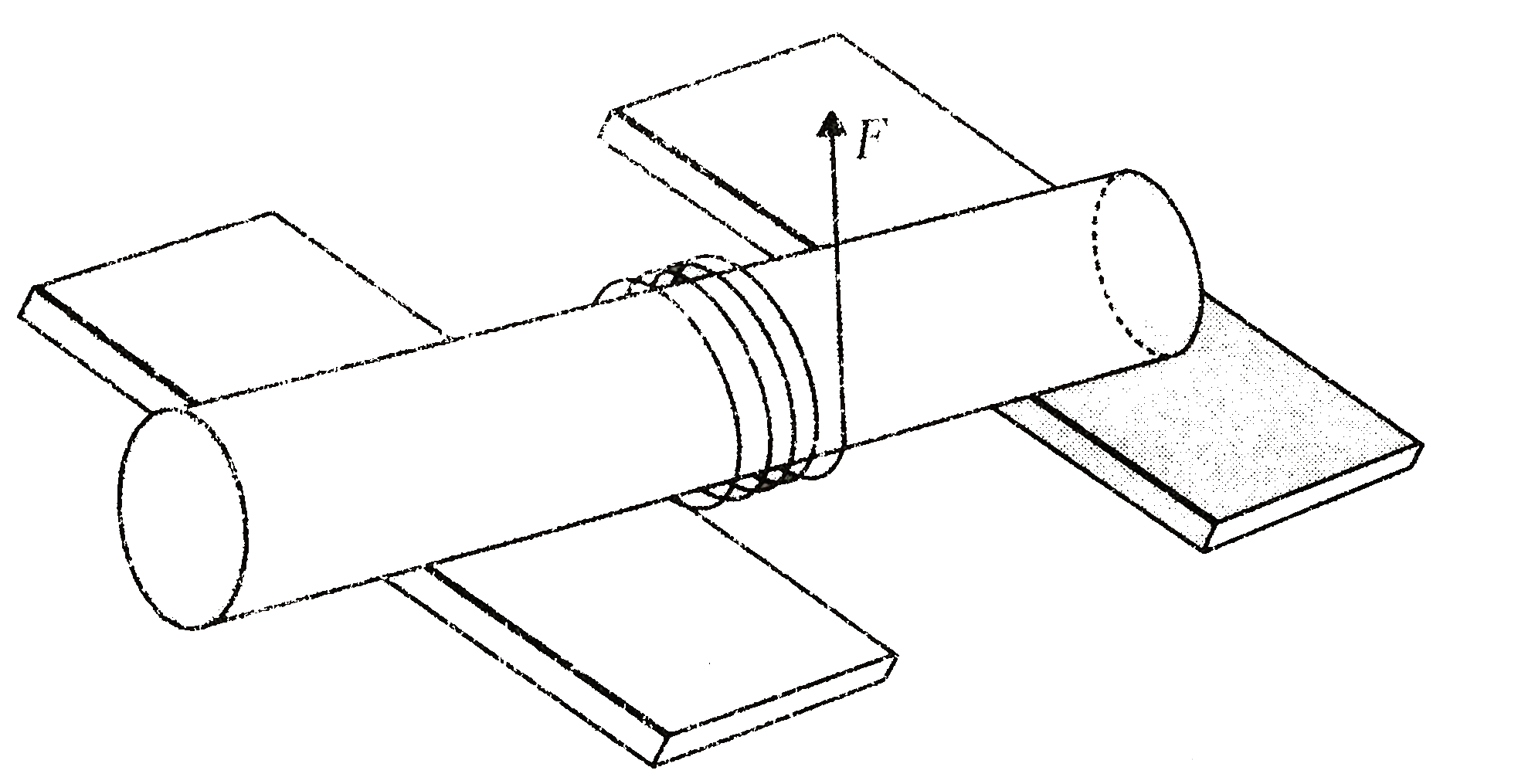
View SolutionA uniform solid cylinder of mass `m` rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force `F`. What is the maximum magnitude of the force `F` which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to `mu`. What is the maximum acceleration of the axis of the cylinder?
View SolutionA bullet of mass `m` moving with a velocity of `u` just grazes the top of a solid cylinder of mass `M` and radius `R` resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View SolutionA small solid marble of mass `M` and radius `r` rolls down along the loop track, without slipping. Find the height `h` above the base, from where it has to start rolling down the incline such that the sphere just completes the vertical circular loop of radius `R`.

View SolutionA solid sphere of mass `M` is placed on the top of a plank of the same mass, after giving an angular velocity `omega_(0)` at `t= 0`. Find the velocity of the plank and the sphere when the sphere starts rolling:,

View SolutionA ball of mass `m` is released from rest from a height `H` along a smooth, light and fixed tube having a semicircular portion so that the ball just reaches the top of the semicircle.
a. Find the radius of the semi-circle.
b. Find the maximum force imparted by the ball on the ground.

View SolutionA sphere of mass `m` and radius `R` rolls without sliding on a horizontal surface. It collides with a light spring of stiffness `K` with a kinetic energy `E`. If the surface (`AB`) under the spring is smooth, find the maximum compression of the spring.
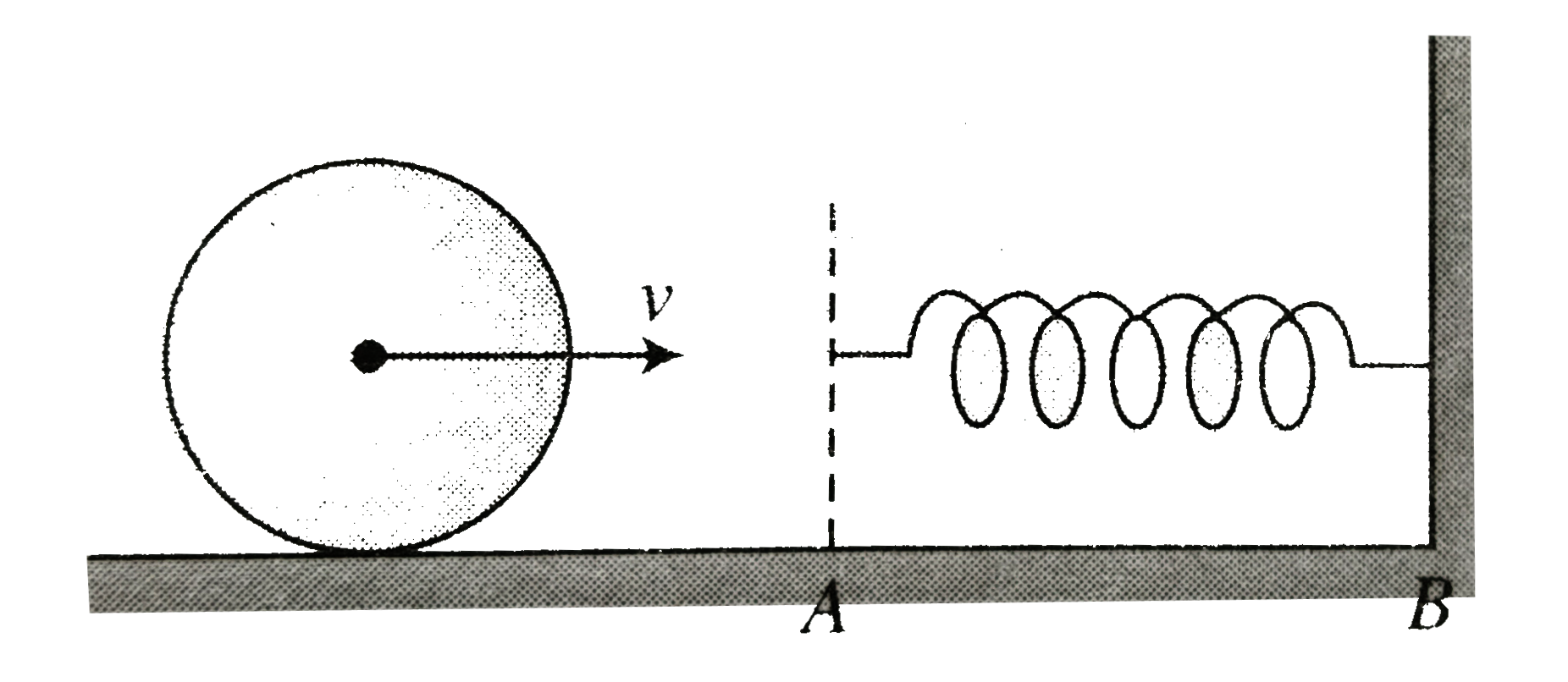
View SolutionFind the acceleration of the body if a force `F=8 N` pulls the string at `P` that passes over the body and it is connected by another string to a rigid support at `Q`.
(Take radius of gyration `k=2/(sqrt(3)) m, R=2m,r=1m,` and mass of the body `m=3kg)`

View SolutionA cotton reel rolls without sliding such that the point `P` of the string has velocity `v = 6 ms^(-1)`. If `r = 10 cm` and `R = 20 cm` then find the:
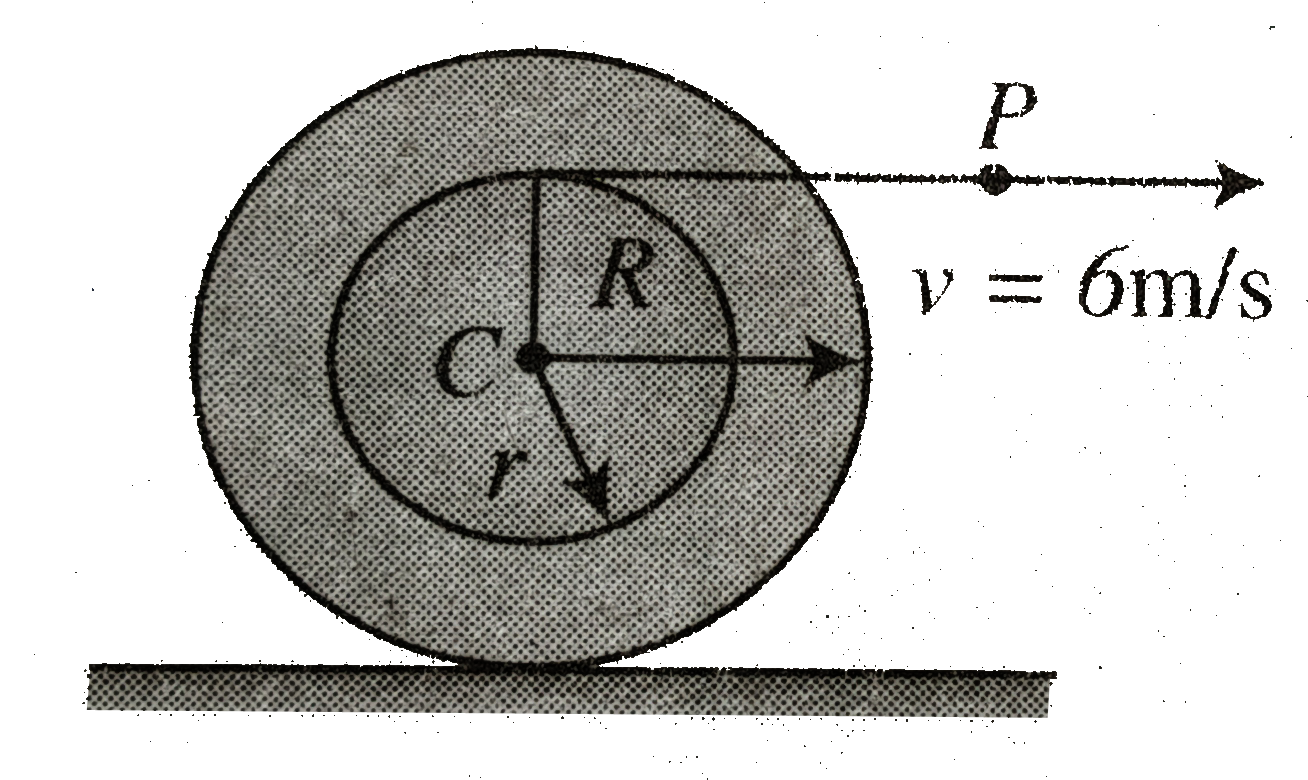
velocity of its centre `C`
View SolutionA cotton reel rolls without sliding such that the point `P` of the string has velocity `v = 6 ms^(-1)`. If `r = 10 cm` and `R = 20 cm` then find the:
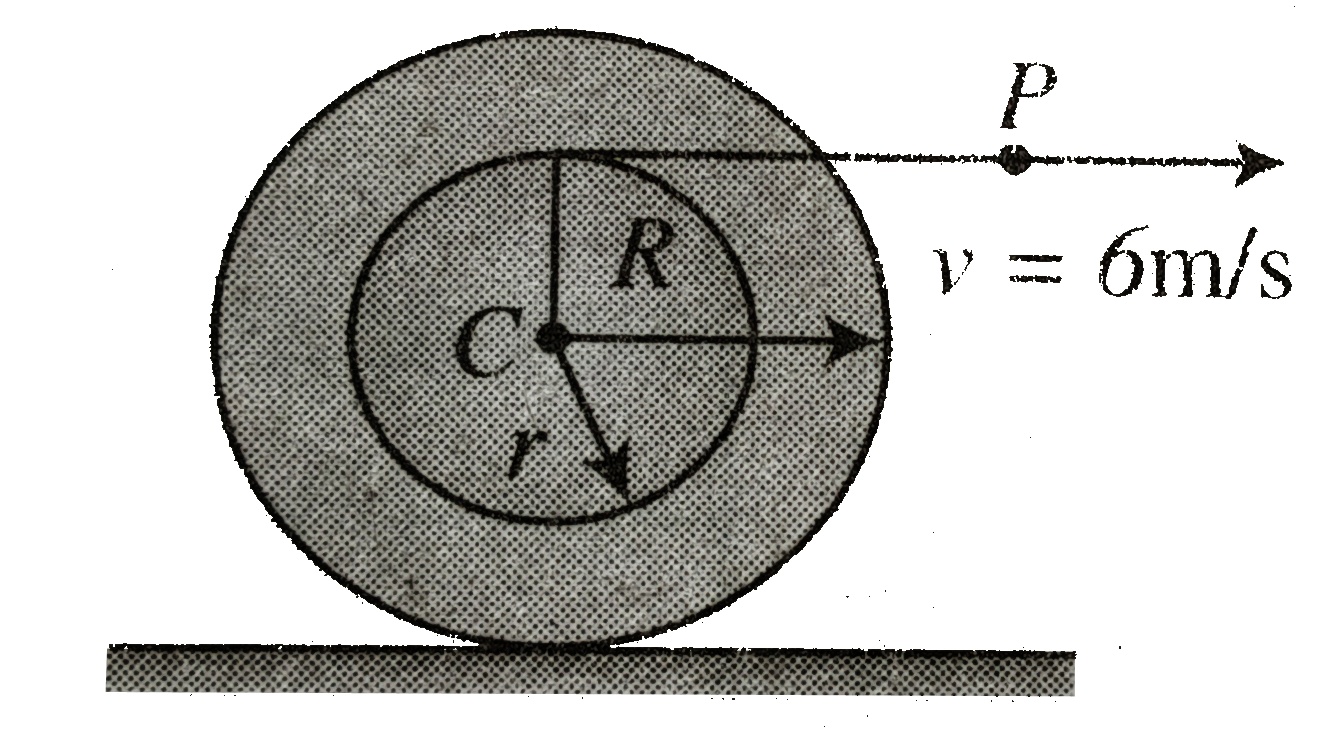
angular velocity of the cotton reel
View SolutionA uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration `a = g//2`, find the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding.

View Solution
Exercise 3.3 questions and complete solutions for chapter RIGID BODY DYNAMICS 2 of CENGAGE PHYSICS (HINGLISH) of Class 11