Complete Solutions to Solved Examples of chapter RIGID BODY DYNAMICS 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Solved Examples |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
A carpet of mass `M` is rolled along its length so as to from a cylinder of radius `R` and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars rolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to `R//2`.
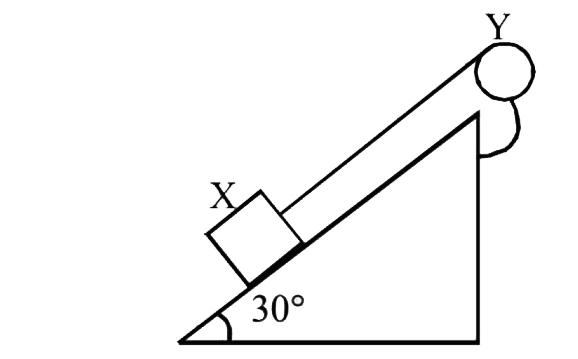
View SolutionA block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination `30^@` to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s `10 rad s^(-1)` calculate the distance travelled by X from that instant of time until it comes to rest
View SolutionA man pushes a cylinder of mass `m_1` with the help of a plank of mass `m_2` as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
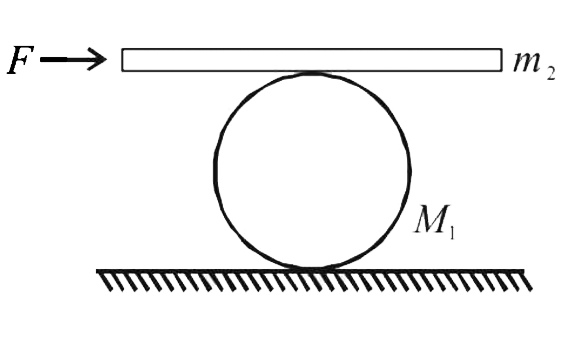
(b) the magnitudes and direction of frictional force at contact points.
View SolutionA plank of mass `M`, is placed on a smooth surface over which a cylinder of mas `m(=M)` annd radius `R=1m` is placed as shown in figure. Now the plane is pulled towards the right wilth an external force `F(=2Mg)`. If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take `g=10 ms^(2)`)

View SolutionA uniform slender bar `B` of mass `m` and length `L` supported by a firctionless `m` and length `L` supported by a firctionless pivot at `A` is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

View SolutionA hoop of mass `m` is projected on a floor with linear velocity `v_(0)` and reverse spin `omega_(0)`. The coefficient of friction between the hoop and the ground is `mu`.
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?
View SolutionA trolley intially at rest with a solid cylinder placed on its bed such that cylinder axis makes angle `theta` with direction of motion of trolley as shown in the figure starts to move forward with constant acceleration a. If initial distance of midpoint of cylinder axis from rear edge of trolley bed is `d`, calculate the distance `s` which the trolley goes before the cylinder rolls off the edge of its horizontal bed. Assume dimensions of cylinder to be very small in comparision to other dimensions. Neglect slipping.
Calculate als, frictional force acting on the cylinder.

View SolutionA uniform solid cylinder of radius `R=15 cm` rolls over a horizontal plane passing into an inclined plane forming an angle `alpha=30^@` with the horizontal. Find the maximum value of the velocity `v_(0)` which still permits the cylinder to roll on the inclined plane section without a jump. (The sliding is assumed to be absent).

View SolutionA solid sphere of radius `R` is set into motion on a rough horizontal surface with a linear speed `v_(0)` in forward direction and an angular with a linear speed `v_(0)` in forward direction and an angular velocity `omega_(0)=v_(0)//2R` in counter clockwise direction as shown in figure. If coefficient of friction `mu` then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
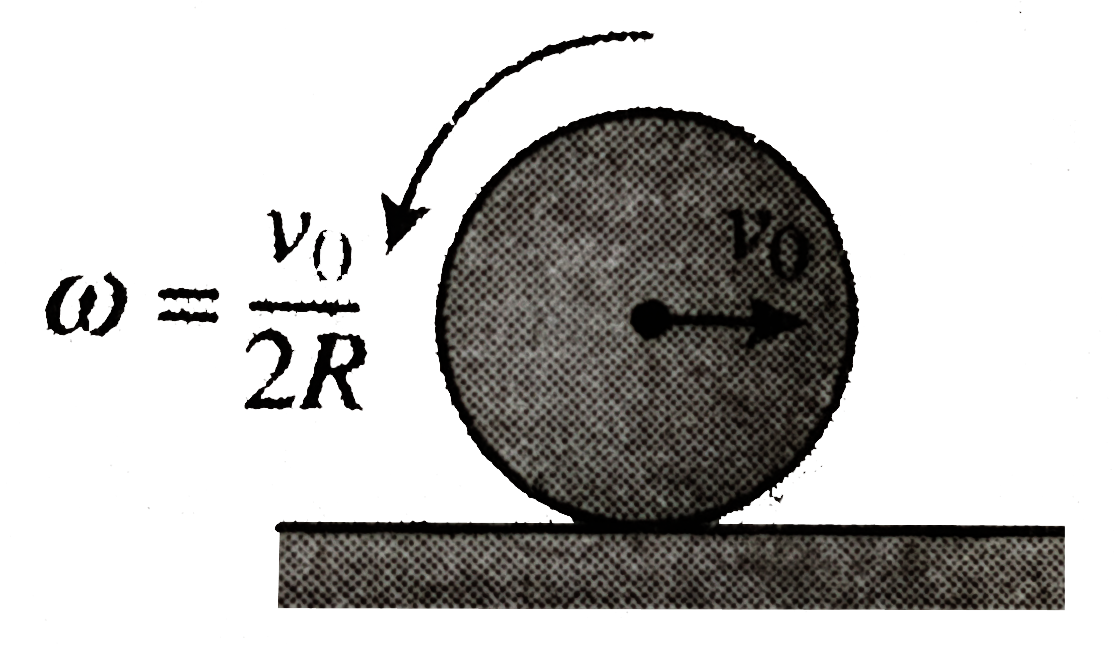
View SolutionA composite rod of mass `2m` and length `2l` comprises two indentica rods joined end to end at `P`. The composite rod hinged at one of its ends is kept horizontal as shown in the figure. If it is realeased from rest.
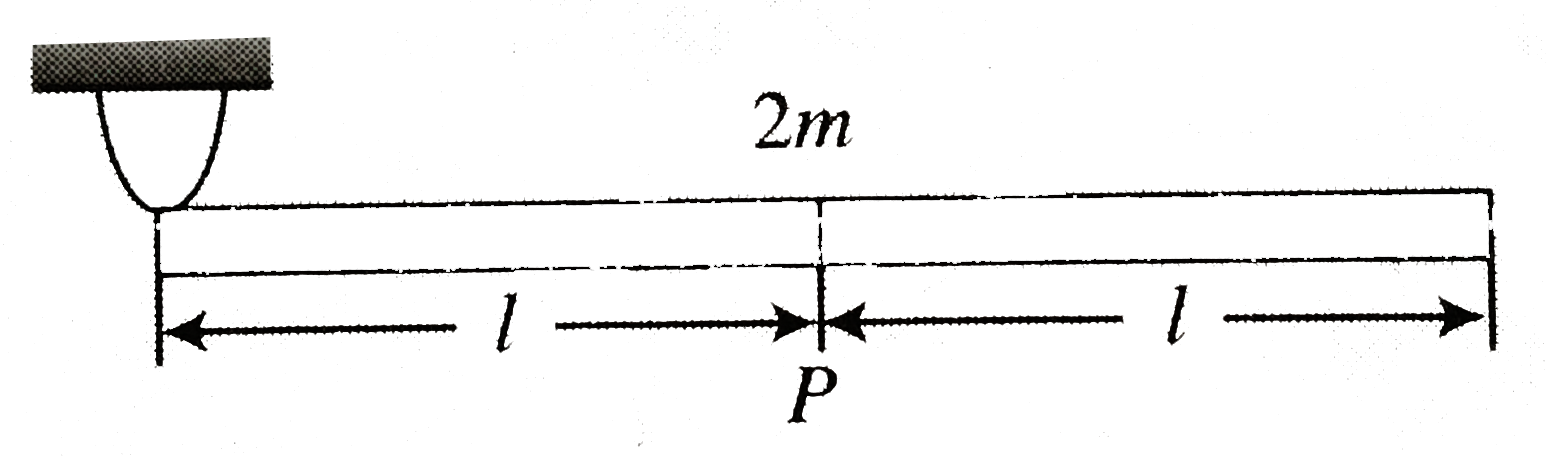
a. find its angular speed when it becomes vertical.
b. If the lower rod gets detached with the upper rod due to centrifugal effect at their joint `P`, at the vertical position of the composite rod, find their linear and angular velocities just after their separation.
View SolutionA ball of radius `R=20 cm` has mass `m=0.75 kg` and moment of inertia (about its diameter ) `I=0.0125 kgm^(2)`. The ball rolls without sliding over a rough horizontal floor with velocity `v_(0)=10 ms^(-1)` towards a smooth vertical wall if coefficient of restitution between the wall and the ball is `e=0.7`, calculate velocity `v` of the ball long after the collision. `(g=10ms^(-2))`
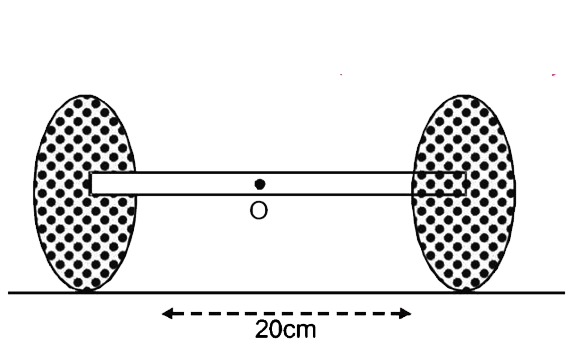
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of `9m//s^2` Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors `hati, hatj and hatk` in the x,y, and z directions.
View Solution
Solved Examples questions and complete solutions for chapter RIGID BODY DYNAMICS 2 of CENGAGE PHYSICS (HINGLISH) of Class 11