Complete Solutions to EXERCIESE of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| HC VERMA | EXERCIESE |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
A uniform slab of dimension `10cmxx10cmxx1cm` is kept between two heat reservoir at temperatures `10^(@)C` and `90^(@)C`. The larger surface areas touch the reservoirs. The thermal conductivity of the material is `0.80Wm^(-1)C^(-1)` . Find the amount of heat flowing through the slab per minute.
View SolutionA liquid-nitrogen container is made of a `1-cm` thick styrofoam sheet having thermal conductivity `0.025Js^(-1)m^(-1)C^(-1)` . Liquid nitrogen at ` 80K` is kept in it. A total area of `0.80m^(2)` is in contact with the liquid nitrogen. The atmospheric temperature is `300K` . Calculate the rate of heat flow from the atmosphere to the liquid nitrogen.
View SolutionThe normal body-temperature of a person is `97^(@)F` . Calculate the rate at which heat is flowing out of his body through the clothes assuming the following values. Room temperature `=47^(@)F` , surface of the body under clothes `=1.6m^(2)` , conductivity of the cloth `=0.04Js^(-1)m^(-1)C^(-1)` , thickness of the cloth `=0.5cm`.
View SolutionWater is boiled in a container having a bottom of surface area `25cm^(2)` , thickness `1.0mm` and thermal conductivity `50Wm^(-1)C^(-1)` , 100g of water is converted into steam per minute in the steady state after the boiling starts. Assuming that no heat is lost to the atmosphere, calculate the temperature of the lower surface of the bottom. Latent heat of vaporization of water `=2.26xx10^(6)Jkg^(-1)` .
View SolutionOne end of a steel rod `(K=46Js^(-1)m^(-1)C^(-1))` of length `1.0m` is kept in ice at `0^(@)C` and the other end is kept in boiling water at `100^(@)C` . The area of cross section of the rod is `0.04cm^(2)` . Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice `=3.36xx10^(5)Jkg^(-1)` .
View SolutionAn icebox almost completely filled with ice at `0^(@)C` is dipped into a large volume of water at `20^(@)C` . The box has walls of surface area `2400cm^(2)` thickness `2.0mm` and thermal conductivity `0.06Wm^(-1)C^(-1)` . Calculate the rate at which the ice melts in the box. Latent heat of fusion of ice `=3.4xx10^(5)Jkg^(-1)` .
View SolutionA pitcher with `1-mm` thick porous walls contain 10kg of water. ,Water comes to its outer surface and evaporates at the rate of `0.1gs^(-1)` . The surface area of the pitcher (one side) `=200cm^(2)` . The room temperature `=42^(@)C` , latent heat of vaporization `=2.27xx10^(6)Jkg^(-1)` , and the thermal conductivity of the porous walls `=0.80js^(-1)m^(-1)C^(-1)` . Calculate the temperature of water in the pitcher when it attains a constant value.
View SolutionA steel frame `(K=45Wm^(-1)C^(-1))` of total length `60cm` and cross sectional area `0.2cm^(2)` , Forms three side of a square. The free ends are maintained at `20^(@)C` and `40^(@)C` . Find the rate of heat flow through a cross section of the frame.
View SolutionWater at `50^(@)C` is filled in a closed cylindrical vessel of height `10cm` and cross sectional area `10cm^(2)` The walls of the vessel are adiabatic but the flat parts are made of `1-mm` thick aluminium `(K=200Js^(-2)m^(-1)C^(-1)` . Assume that the outside temperature is `20^(@)C` . The density of water is `1000kgm^(-3)` and the specify heat capacity of water `=4200Jkg^(-1)C^(-1)` .Estimate the time taken for the temperature to fall by `1.0^(@)C` . Make any simplifying assumption you need but specify them.
View SolutionThe left end of a copper rod (length=`20cm`, Area of cross section=`0.2cm^(2)`) is maintained at `20^(@)C` and the right end is maintained at `80^(@)C` . Neglecting any loss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper `=385Wm^(-1)C^(-1)` .
View SolutionThe ends of a metre stick are maintain at `100^(@)C` and `0^(@)C` . One end of a rod is maintained `25^(@)C` . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionA cubical box of volume `216cm^(3)` is made up of `0.1cm` thick wood, The inside is heated electrically by 100W heater. It is found that the temperature difference between the inside and the outside surface `5^(@)C` in steady state . Assuming that the entire electrically energy spent appears as heat, find the thermal conductivity of the material of the box.
View SolutionFigure shows water in a container having `2.0-mm` thick walls made of a material of thermal conductivity `0.50Wm^(-1)C^(-1)` . The container is kept in a melting-ice bath at `0^(@)C` . The total surface area in contact with water is`0.05m^(2)` . A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of `10cms^(-1)` and the temperature of the water remains constant at `1.0^(@)C` .Find the mass M of the block. Assume that the heat flow out of the water only through the walls in contact. Take `g=10ms^(-2)` .

View SolutionOn a winter day when the atmospheric temperature drops to `-10^(@)C` , ice forms on the surface of a lake. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches `0^(@)C` before the ice starts forming. Density of water `=1000kgm^(-3)` , latent heat of fusion of ice `=3.36xx10^(5)Jkg^(-1)` and thermal conductivity of ice `=1.7Wm^(-1)C^(-1)` . Neglect the expansion of water on freezing.
View SolutionConsider the situation of the previous problem. Assume that the temperature of the water at the botton of the lake remains constant at `4^(@)C` as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is `1.0m`. Show that the thickness of the ice formed attains a steady state maximum value. Find this value. The thermal conductivity of water `=0.50Wm ^(-1).^(@)C^(-1)` . Take other relevent data form the previous problelm.
View SolutionThree rods of lengths 20cm each and area of cross section `1cm^(2)` are joined to from a triangle ABC. The conductivities of the rods are `k_(AB)=50Js^(-1)m^(-1)C^(-1)` , `k_(BC)=200Js^(-1)m^(-1)C^(-1)` , and `k_(AC)=400Js^(-1)m^(-1)C^(-1)` . The junction A,B and C are maintained at `40^(@)C` , `80^(@)C` and `80^(@)C` respectively. Find the rate of heat flowing through the rods AB, AC and BC .
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the straight rod in a given time.
View SolutionA metal rod of cross sectional area `1.0cm^(2)` is being heated at one end. At one time , the temperature gradient is `5.0^(@)C cm^(-1)` at cross section A and is `2.5^(@)Ccm^(-1)` at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB`=0.40J^(@)C^(-1)` , thermal conductivity of the material of the rod. `K=200Wm^(-1)C^(-1)` . Neglect any loss of heat to the atmosphere.
View SolutionSteam at `120^(@)C` is continuously passed through a `50-cm` long rubber tube of inner and outer radii `1.0cm` and `1.2cm` . The room temperature is `30^(@)C` . Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber `= 0.15Js^(-1)m^(-1)C^(-1)` .
View SolutionA hole of radius `r_(1)` is made centrally in a uniform circular disc of thickness d and radius `r_(2)` . The inner surface (a cylinder of length d and radius `r_(1)`) is maintained at a temperature `theta_(1)` and the outer surface (a cylinder of length d and radius `r_(2)`) is maintained at a temperature `theta_(2)(theta_(1)gttheta_(2))` .The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
View SolutionA hollow tube has a length l, inner radius `R_(1)` and outer radius `R_(2)` . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature `T_(1)` and `T_(2)``(T_(2)gtT_(1))` (b) the inside of the tube is maintained at temperature `T_(1)` and the outside is maintained at `T_(2)` .
View SolutionA composite slab is prepared by pasting two plates of thickness `L_(1)` and `L_(2)` and thermal conductivities `K_(1)` and `K_(2)` . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at `0^(@)C` and that of the steel rod is kept at `100^(@)C` . Find the temperature at the junction of the rods. conductivity of copper `=390Wm^(-1)C^(-1)` and that of steel `=46Wm^(-1)C^(-1)` .

View SolutionAn aluminium rod and a copper rod of equal length `1.0 m` and cross-sectional area. `1cm^(2)` are welded together as shown in figure. One end is kept at a temperature of `20^(@)C` and the other at `60^(@)C` Calculate the amount of heat taken out per second from the hot end. thermal conductivity of aluminium `=200Wm^(-1)C^(-1)` and of copper `=390Wm^(-1)C^(-1)` .

View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of cross section `0.20cm^(2)` . The junction is maintained at a constant temperature `40^(@)C` and the two ends are maintained at `80^(@)C` . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are `K_(Al)=200Wm^(-1)C^(-1)` . and `K_(Cu)=400Wm^(-1)C^(-1)` .

View SolutionConside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at `100^(@)C` is `130J` .
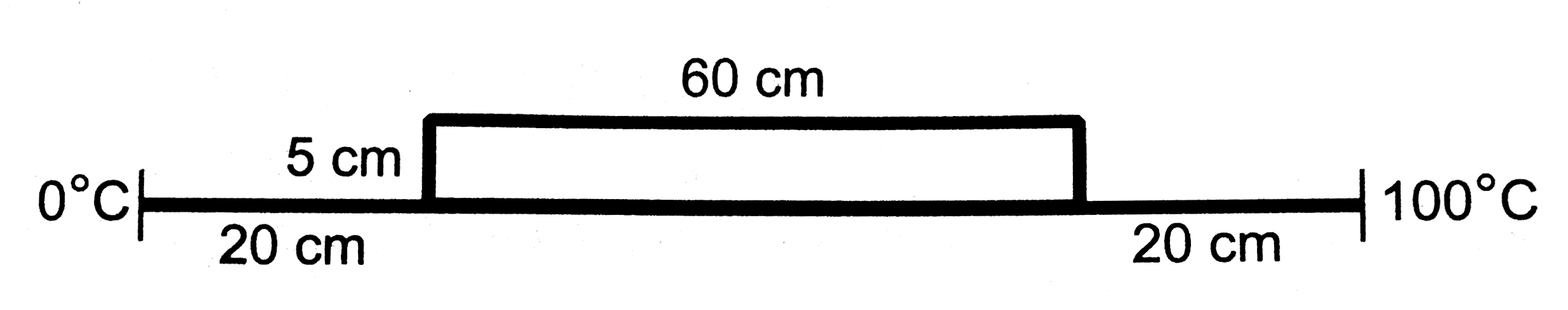
View SolutionSuppose the bent part of the frame of the previous problem has a thermal conductivity of `780s^(-1)m^(-1).^(@)C^(-1)` whereas it is `390Js^(-1)m^(-1).^(@)C^(-1)` for the straight the bent part to the rate of heat flow through the straight part.
View SolutionA room has s window fitted with a single `1.0mxx2.0m` glass of thickness 2mm. (a) Calculate the rate of heat flow through the closed window when the temperature inside the room is `32^(@)C` and that outside is `40^(@)C` . (b) The glass is now replaced by two glasspanes, each having a thickness of 1mm and separated by a distance of 1mm. Calculate the rate of heat flow under the same condition of temperature. Thermal conductivity of window glass `=1.0Js^(-1)m^(-1)C^(-1)` and that of air `=0.025Js^(-1)m^(-1)C^(-1)` .
View SolutionThe two rods show in figure have identical geometrical dimension.. They are in contact with two heat baths at temperature `100^(@)C` . And `0^(@)C` . The temperature of the junction is `70^(@)C` . Find the temperature of the junction if the rods are interchanged.

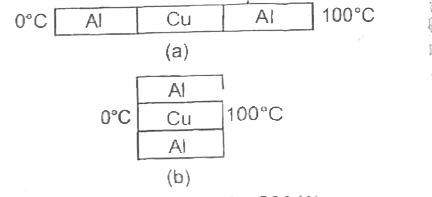
View SolutionThe three rods shown in figure have identical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b). (Assume `k_(Al) = 200 W/(m ^(@)C)` and `K_(Cu) = 400 W/(m ^(@)C)`
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature `T_(1)` , `T_(2)` and `T_(3)` respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionSeven rods A, B, C, D, E, F and G are joined as shown in figure. All the rods have equal cross-sectional area A and length l. The thermal conductivities of the rods are `K_(A)=K_(C)=K_(0)`, `K_(B)=K_(D)=2K_(0)`, `K_(E)=3K_(0)`, `K_(F)=4K_(0)` and `K_(G)=5K_(0)` . The rod E is kept at a constant temperature `T_(1)` and the rod G is kept at a constant temperature `T_(2)``(T_(2)gtT_(1))` . (a) Show that the rod F has a uniform temperature `T=(T_(1)+2T_(2))//3` . (b) Find the rate of heat flowing from the source which maintains the temperature `T_(2)` .

View SolutionFind the rate of heat flow through a cross section of the rod shown in figure `(theta_(2)gttheta_(1))` . Thermal conductivity of the material of the rod is K.

View SolutionA rod of negligible heat capacity has length 20cm, area of cross section `1.0cm^(2)` and thermal conductivity `200Wm^(-1)C^(-1)` . The temperature of one end is maintained at `0^(@)C` and that of the other end is slowly and linearly varied from `0^(@)C` to `60^(@)C` in 10 minutes. Assuming no loss of heat through the sides, find the total heat transmitted through the rod in these 10 minutes.
View SolutionA hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at `50^(@)C` and `10^(@)C` respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

View SolutionTwo bodies of masses `m_(1)` and `m_(2)` and specific heat capacities `S_(1)` and `S_(2)` are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time `t=0` , the temperature of the first body is `T_(1)` and the temperature of the second body is `T_(2)(T_(2)gtT_(1))` . Find the temperature difference between the two bodies at time t.
View SolutionAn amount n (in moles) of a monatomic gas at initial temperature `T_(0)` is enclosed in a cylindrical vessel fitted with a light piston. The surrounding air has a temperature `T_(s)(gtT_(0))` . And the atmospheric pressure is `P_(a)` . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
View SolutionAssume that the total surface area of a human body is `1.6m^(2)` and that it radiates like an ideal radiator. Calculate the amount of energy radiates per second by the body if the body temperature is `37^(@)C` . Stefan constant `sigma` is `6.0xx10^(-8)Wm^(-2)K^(-4)` .
View SolutionCalculate the amount of heat radiated per second by a body of surface area `12cm^(2)` kept in thermal equilibrium in a room at temperature `20^(@)C` The emissivity of the surface `=0.80` and `sigma=6.0xx10^(-s)Wm^(-2)K^(-4)` .
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emisssivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of heat loss from the copper sphere and (b) the rate of fall of temperature of the aluminium sphere to the rate of fall of temperature of copper sphere. The specific heat capacity of aluminium `=900Jkg^(-1)C^(-1)` . and that of copper `=390Jkg^(-1)C^(-1)` . The density of copper `=3.4` times the density of aluminium.
View SolutionA 100W bulb has tungsten filament of total length `1.0m` and raidius `4xx10^(-5)m` . The emiswsivity of the filament is `0.8` and `sigma=6.0xx10^(-8)Wm^(-2)K^(-4)` . Calculate the temperature of the filament when the bulb is oprating at correct wattage.
View SolutionA spherical ball of surface area `20cm^(2)` absorbs any radiation that falls on it. It is suspended in a closed box maintained at `57^(@)C` . (a) Find the amount of radiation falling on the ball per second. (b) Find the net rate of heat flow to or from the ball at an instant when its temperature is `200^(@)C` . Stefan constant `=6.0xx10^(-s)Wm^(-2)K^(-4)` .
View SolutionA spherical tungsten pieces of radius `1.0cm` is suspended in an evacuated chamber maintained at `300K`. The pieces is maintained at 1000K by heating it electrically. Find the rate at which the electrical energy must be supplied. The emissivity of tungsten is `0.30` and the Stefan constant `sigma` is `6.0xx10^(-s)Wm^(-2)K^(-4)` .
View SolutionA cubical block of mass `1.0kg` and edge `5.0cm` is heated to `227^(@)C` . It is kept in an evacuated chamber maintained at `27^(@)C` . Assming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is `400Jkg^(-1)K^(-1)` .
View SolutionA copper sphere is suspended in an evacuated chamber maintained at 300K. The sphere is maitained at a constant temperature of 500K by heating it electrically. A total of 210W is electric power is needed to do it. When the surface of the copper sphere is completely blackned, 700W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.
View SolutionA spherical ball A of surface area `20cm^(2)` is kept at the centre of a hollow spherical shell B of area `80cm^(2)` . The surface of A and the inner surface of B emit as blackbodies. Both A and B are at 300K. (a) How much is the radiation energy emitted per second by the ball A? (b) How much is the radiation energy emitted per second by the inner surface of B? (c) How much of the energy emitted by the inner surface of B falls back on this surface itself?
View SolutionA cylindrical rod of length 50cm and cross sectional area `1cm^(2)` is fitted between a large ice chamber at `0^(@)C` and an evacuated chamber maintained at `27^(@)C` as shown in figure. Only small protions of the rod are insid ethe chamber and the rest is thermally insulated from the surrounding. The cross section going inti the evacuted chamber is blackened so that it completely absorbe any radiation falling on it. The temperatuere of the blackened end is `17^(@)C` when steady state is reachhed. Stefan constant `sigma=6xx10^(-s)Wm^(-2)K^(-4)` . Find the thermal conductivity of the material of the rod.

View SolutionOne end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant `sigma=6.0xx10^(-1)Wm^(-2)K^(-4)` .
View SolutionA calorimeter of negligible heat capacity contains 100cc of water at `40^(@)C` . The water cools to `35^(@)C` in 5minutes. The water is now replaced by k-oil of equal volume at `40^(@)C` . Find the time taken for the temperature to become `35^(@)C` under similar conditions. Specific heat cpacities of water and K-oil are `4200Jkg^(-1)K^(-1)` and `2100Jkg^(-1)K^(-1)` respectively. Density of K-oil `=800kgm^(-3)` .
View SolutionA body cools down from `50^(@)C` to `45^(@)C` in 5 minutes and to `40^(@)C` in another 8 minutes. Find the temperature of the surrounding.
View SolutionA calorimeter containes 50g of water at `50^(@)C` . The temperature falls to `45^(@)C` in 10 minutes. When the calorimeter contains 100g of water at `50^(@)C` it takes 18 minutes for the temperature to become `45^(@)C` . Find the water equivalent of the calorimeter.
View SolutionA metal ball of mass `1kg` is heated by means of a `20W` heater in a room at `20^(@)C` . The temperature of the ball becomes steady at `50^(@)C` . (a) Find the rate of loss of heat to the surrounding when the ball is at `50^(@)C` . (b) Assuming Newton's law of cooling, calculate the rate of loss of heat to the surrounding when the ball is at `30^(@)C` . (c) Assume that the temperature of the ball rises uniformly from `20^(@)C` to `30^(@)C` in `5` minutes. Find the total loss of heat to the surrounding during this period. (d) Calculate the specific heat capacity of the metal.
View SolutionA metal block of heat capacity `90J//.^(@)C` placed in a room at `25^(@)C` is heated electrically. The heater is switched off when the temperature reaches `35^(@)C`. The temperature of the block rises at the rate of `2^(@)C//s` just after the heater is switched on and falls at the rate of `0.2^(@)C//s` just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is `30^(@)C`. (d) Assuming that the power radiated at `30^(@)C` respresents the average value in the heating process, find the time for which the heater was kept on.
View SolutionA hot body placed in a surrounding of temperature `theta_(0)` obeys Newton's law of cooling `(d theta)/(dt)=-k(theta-theta_(0))` . Its temperature at `t=0` is `theta_(1)` the specific heat capacity of the body is `s` and its mass is `m`. Find
(a) the maximum heat that the body can lose and
(b) the time starting from `t=0` in which it will lose `90%` of this maximum heat.
View Solution
EXERCIESE questions and complete solutions for chapter HEAT TRANSFER of HC VERMA PHYSICS (ENGLISH) of Class 11