Complete Solutions to Level-V (Comprehension) of chapter WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK POWER AND ENERGY |
| NARAYANA | Level-V (Comprehension) |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
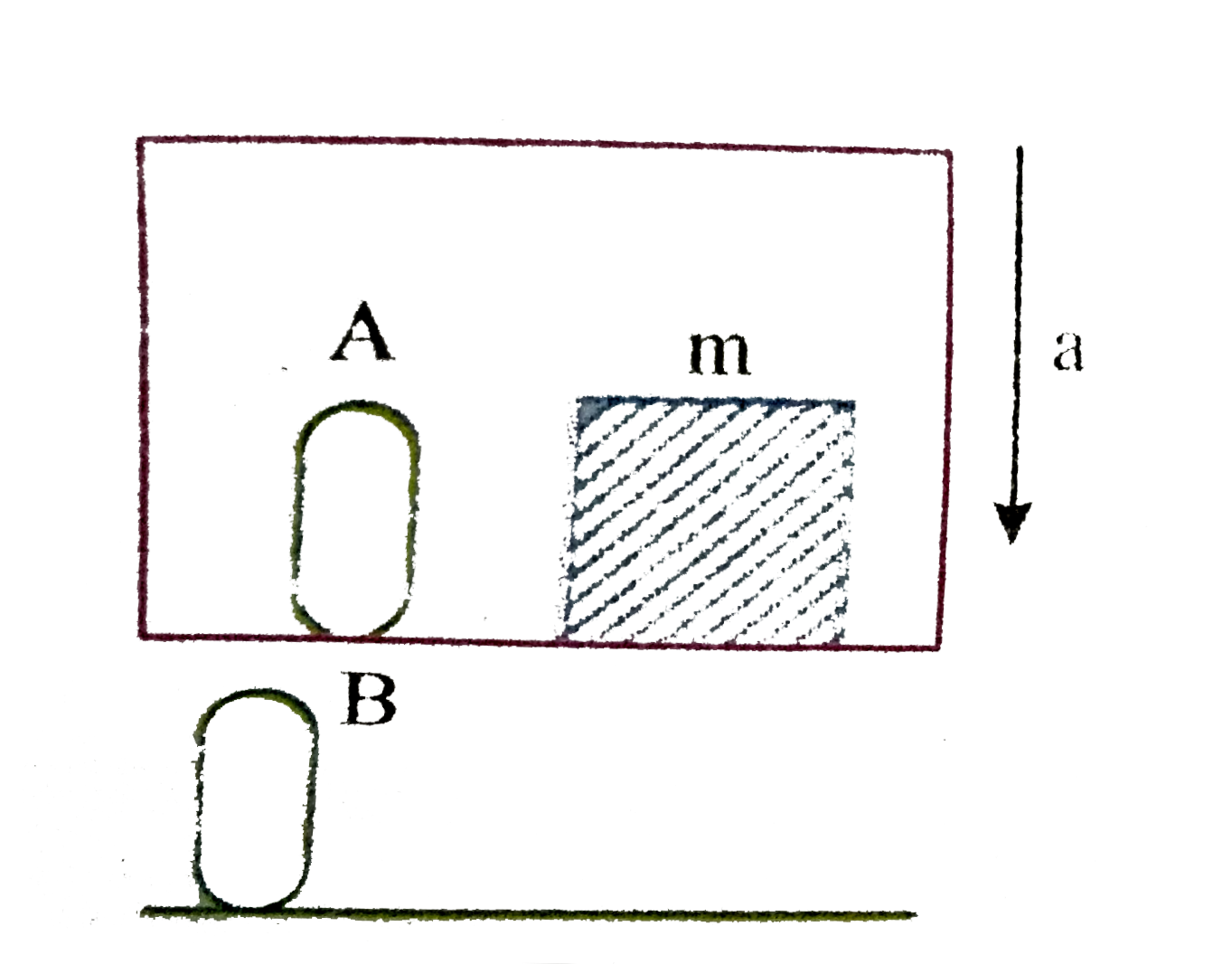
A block of mass `m` is kept in an elevation which starts moving downward with an acceleration 'a' as shown in figure. The block is observed by two observers `A` and `B` for a time interval `t_(0)`.
 .
.
The observer `B` finds that the work done by gravity on the block is :
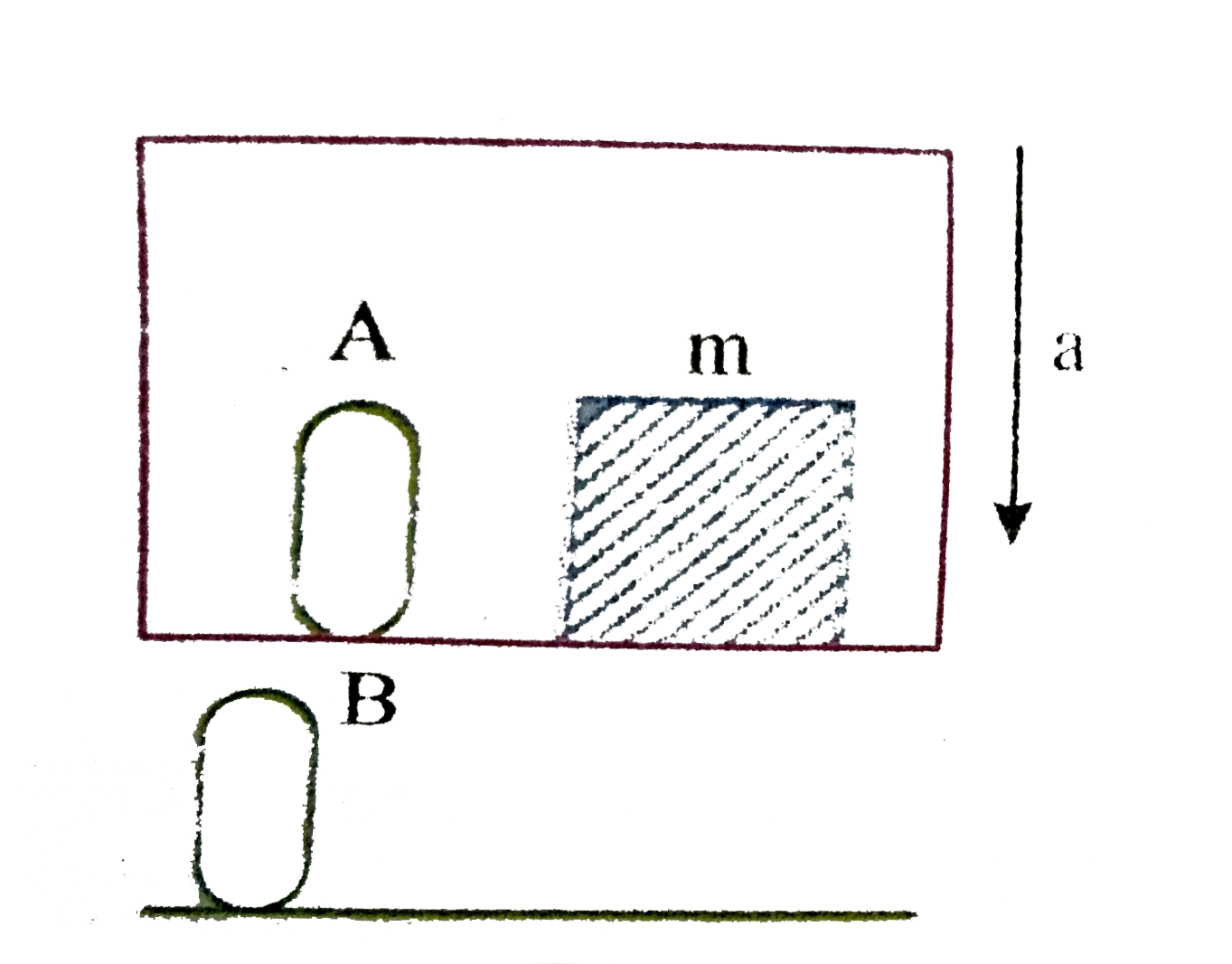
View SolutionA block of mass `m` is kept in an elevation which starts moving downward with an acceleration 'a' as shown in figure. The block is observed by two observers `A` and `B` for a time interval `t_(0)`.
 .
.
The observer `B` finds that the work done by pseodo-force on the block is
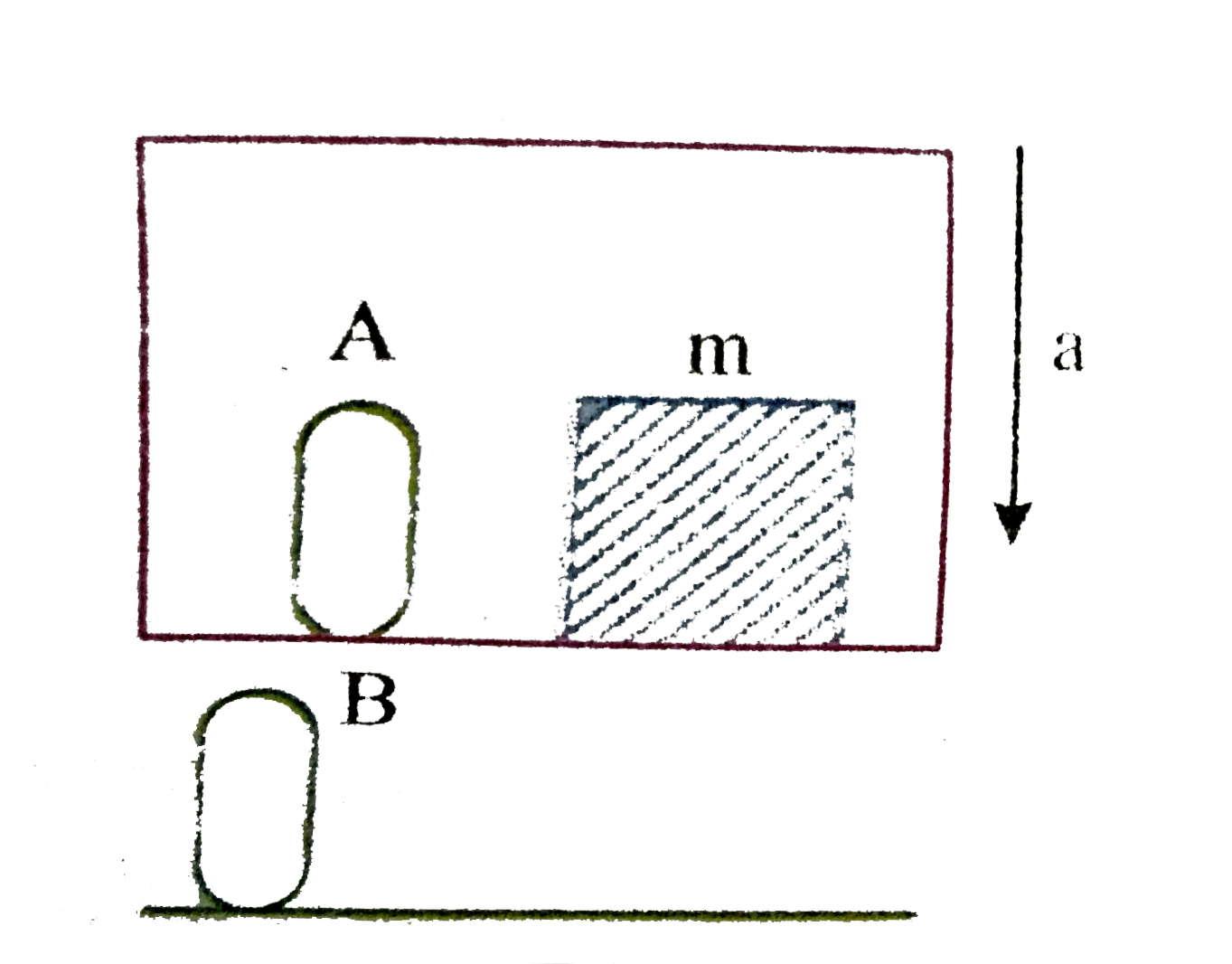
View SolutionA block of mass `m` is kept in an elevation which starts moving downward with an acceleration 'a' as shown in figure. The block is observed by two observers `A` and `B` for a time interval `t_(0)`.
 .
.
According to observer `B`, the net work done on the block is :
View SolutionForce acting on a particle moving in the x-y plane is `vecF=(y^2hati+xhatj)N`, x and y are in metre. As shown in figure, the particle moves from the origin O to point A `(6m, 6m)`. The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
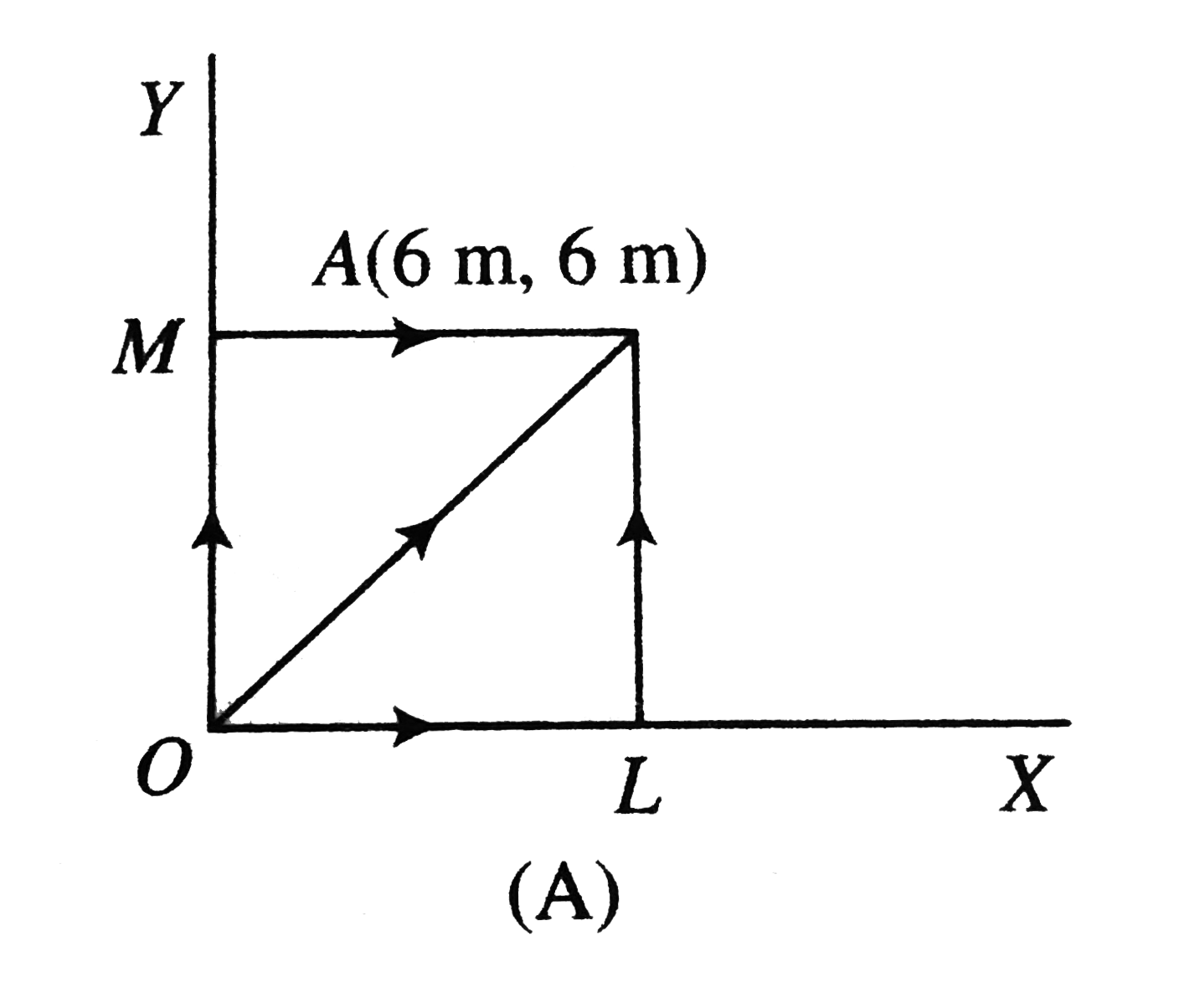
Which of the following is correct?
View SolutionForce acting on a particle moving in the `x-y` plane is `vec F=(y^(2) hat i + x hat j) N, x` and `y` are in metre. As shown in fig. the particle moves from the origin `O` to point `A(6m,6m)`. The figure shows three paths, `OLA,OMA` and `OA` for the motion of the particle from `O` to `A`.
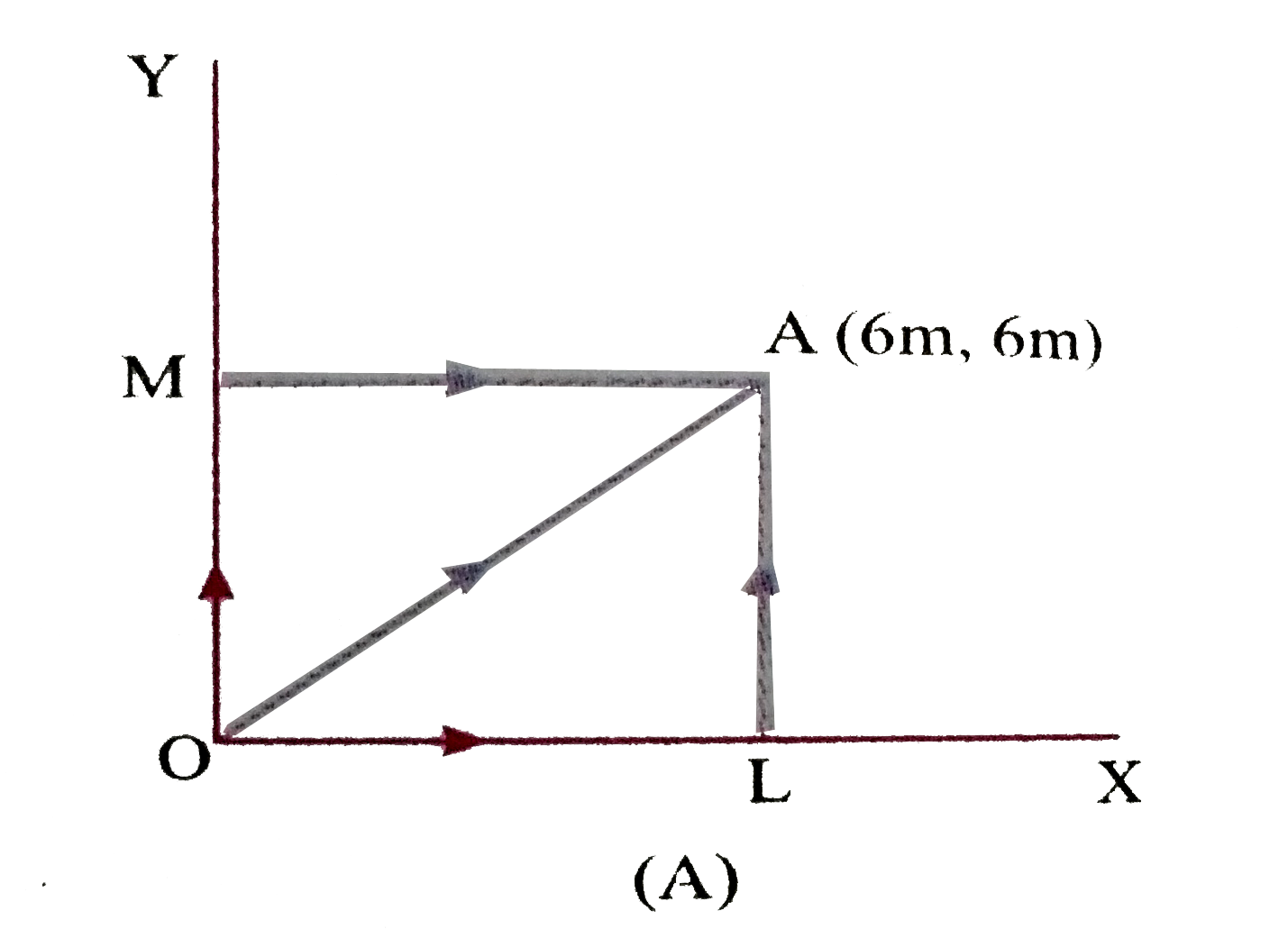
Along which of the three paths is the work done maximum.
View SolutionForce acting on a particle moving in the `x-y` plane is `vec F=(y^(2) hat i + x hat j) N, x` and `y` are in metre. As shown in fig. the particle moves from the origin `O` to point `A(6m,6m)`. The figure shows three paths, `OLA,OMA` and `OA` for the motion of the particle from `O` to `A`.
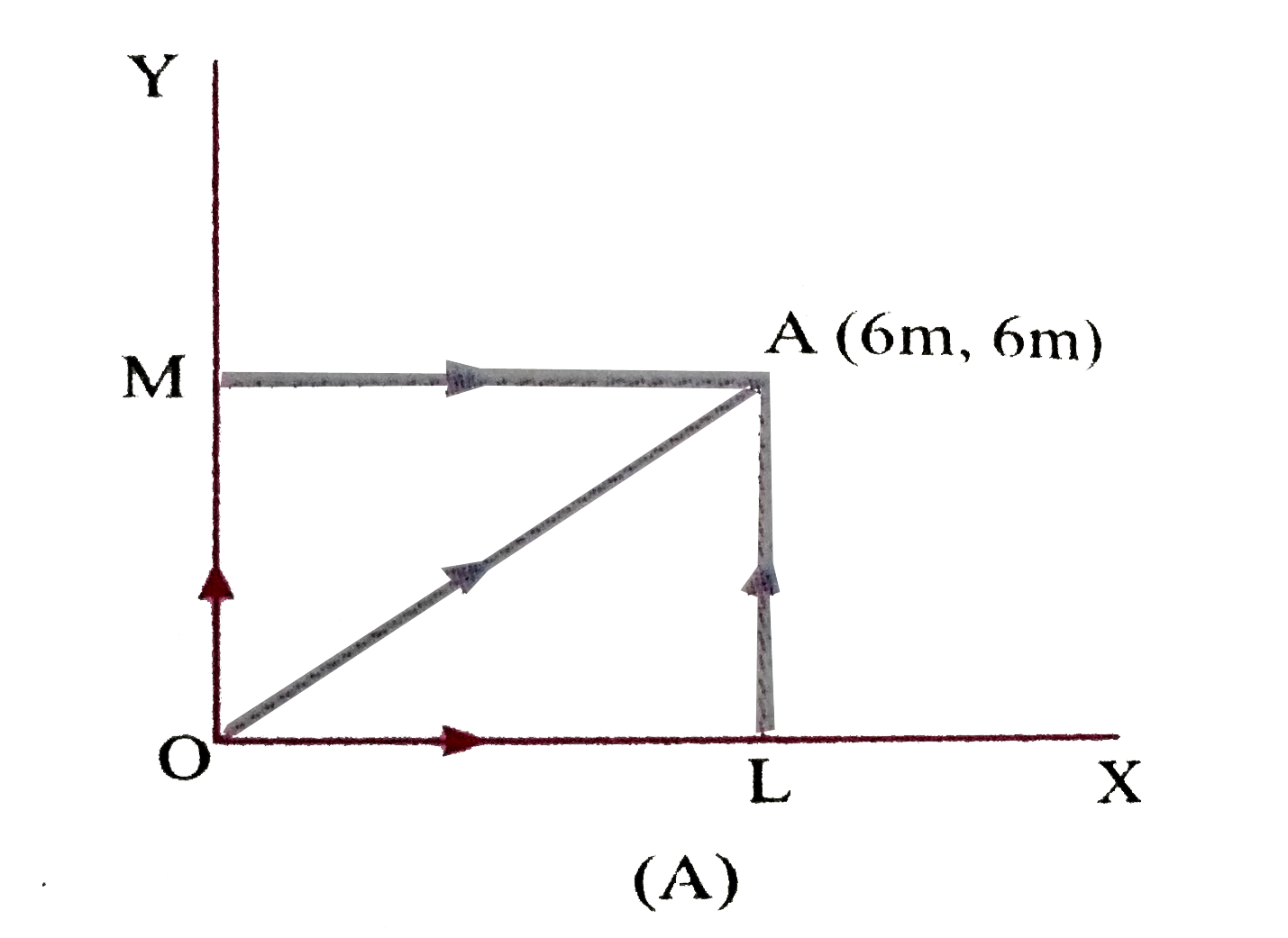
Work done for motion along path `OA` is nearly
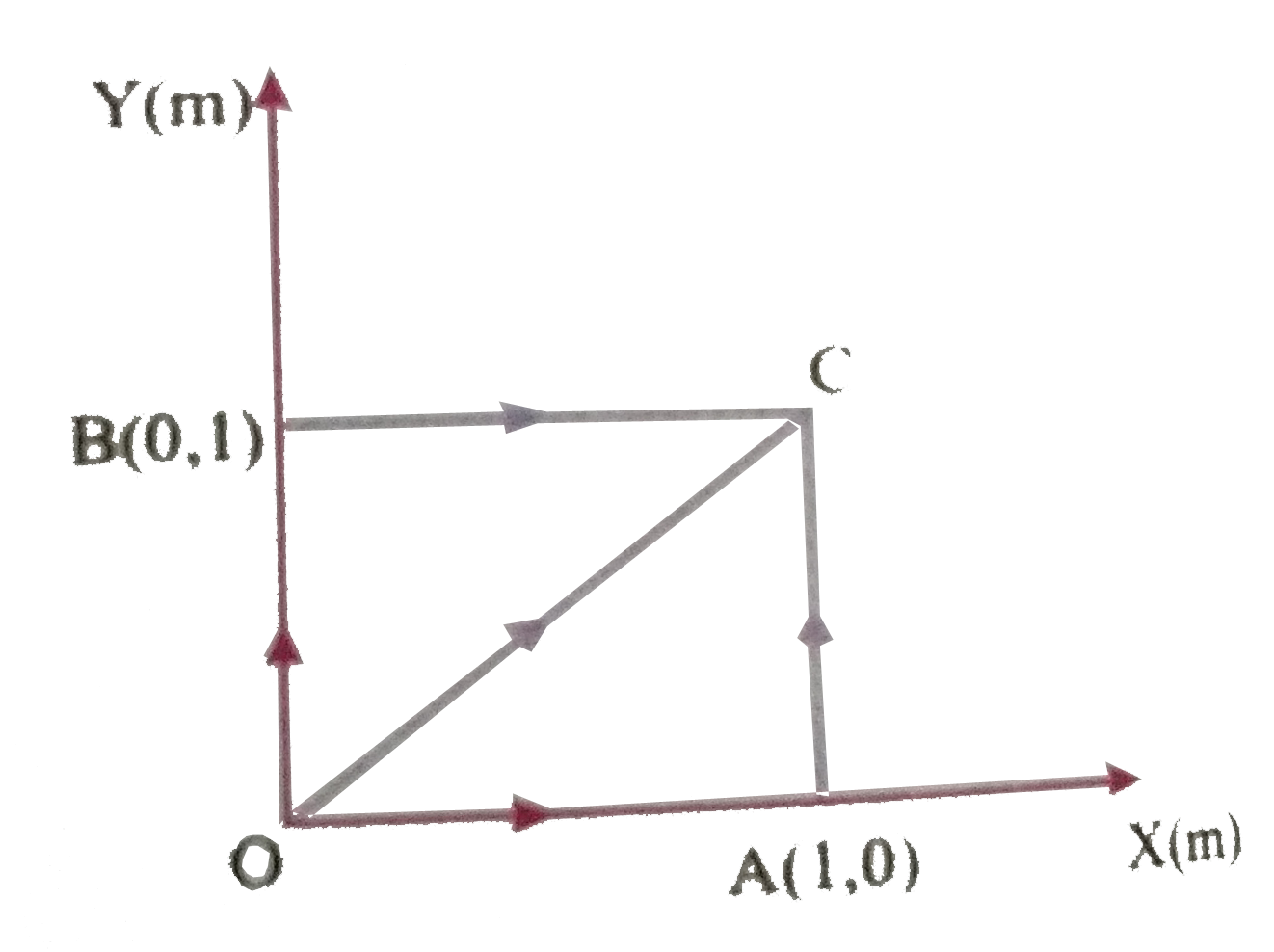
View SolutionOne of the forces acting on a certain particle depends on the particle's position in the `xy`-plane. This force `vec F` expressed in newtons, is given by the expression `vec F = (xy hat i+ xy hat j)` where `x` and `y` are in metres. The particle is moved from `O` to `C` through three different paths :-
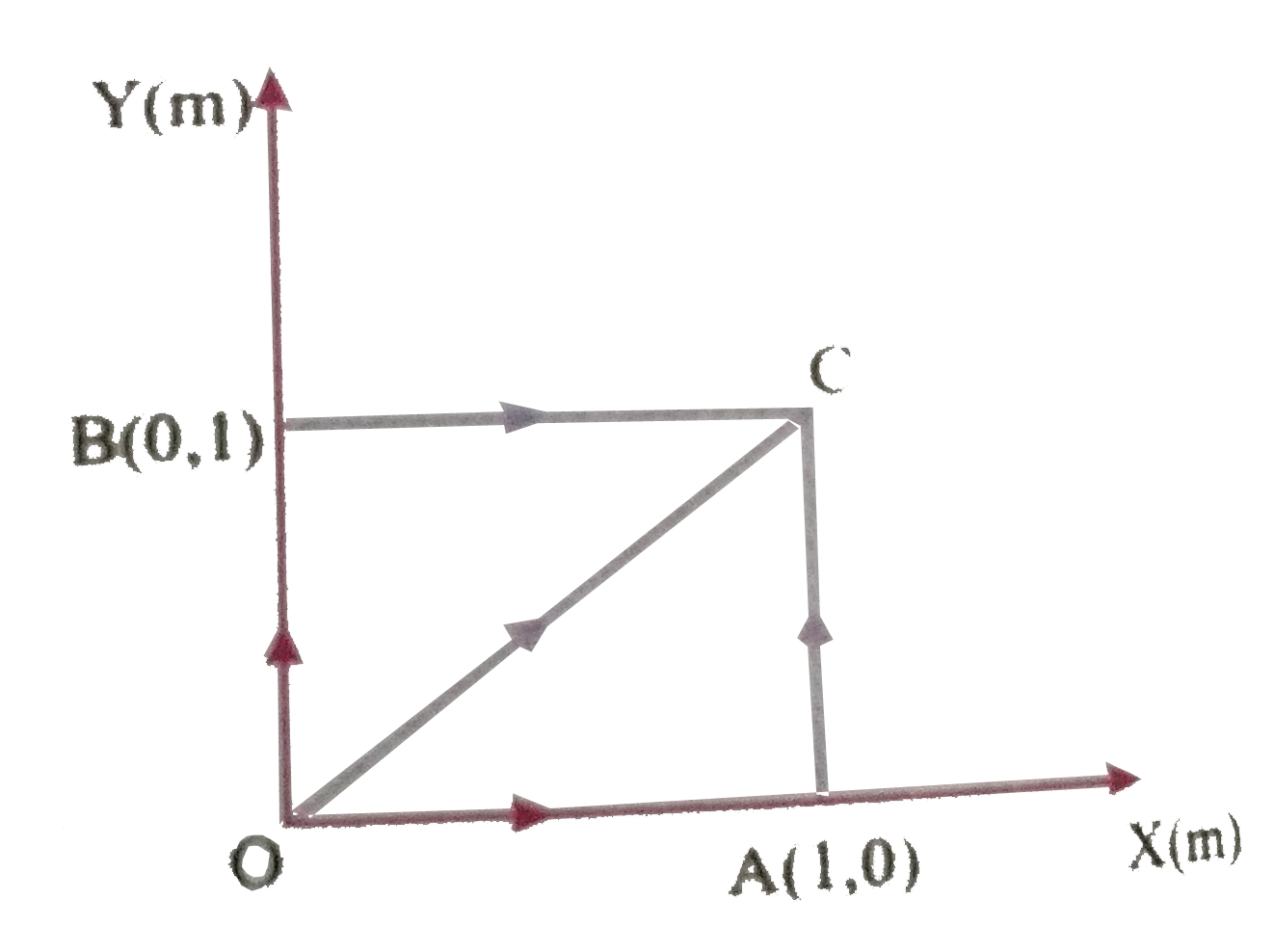
The work done by this force on path `OC` is
View SolutionOne of the forces acting on a certain particle depends on the particle's position in the `xy`-plane. This force `vec F` expressed in newtons, is given by the expression `vec F = (xy hat i+ xy hat j)` where `x` and `y` are in metres. The particle is moved from `O` to `C` through three different paths :-
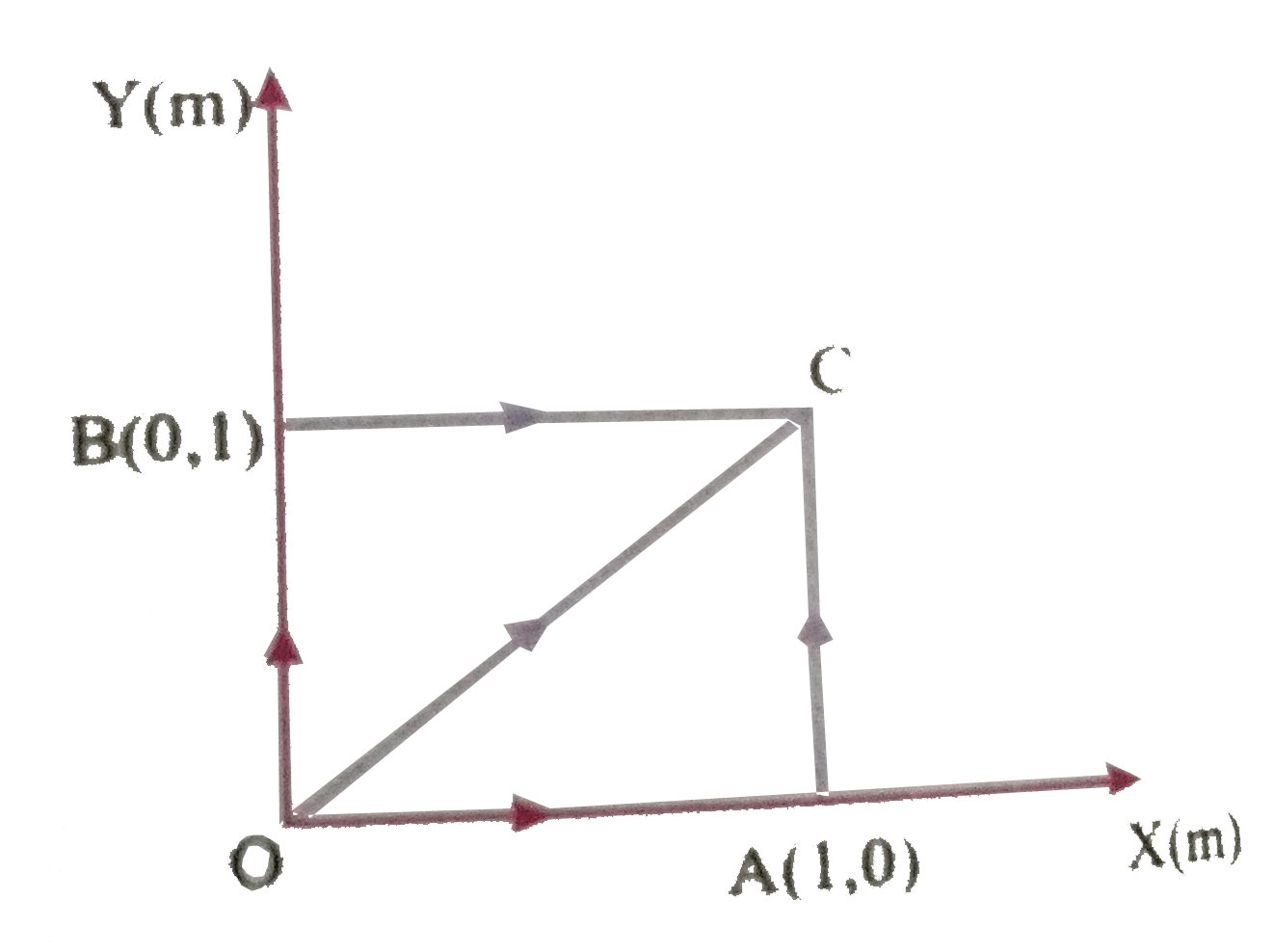
The work done by this force on path `OAC` is.
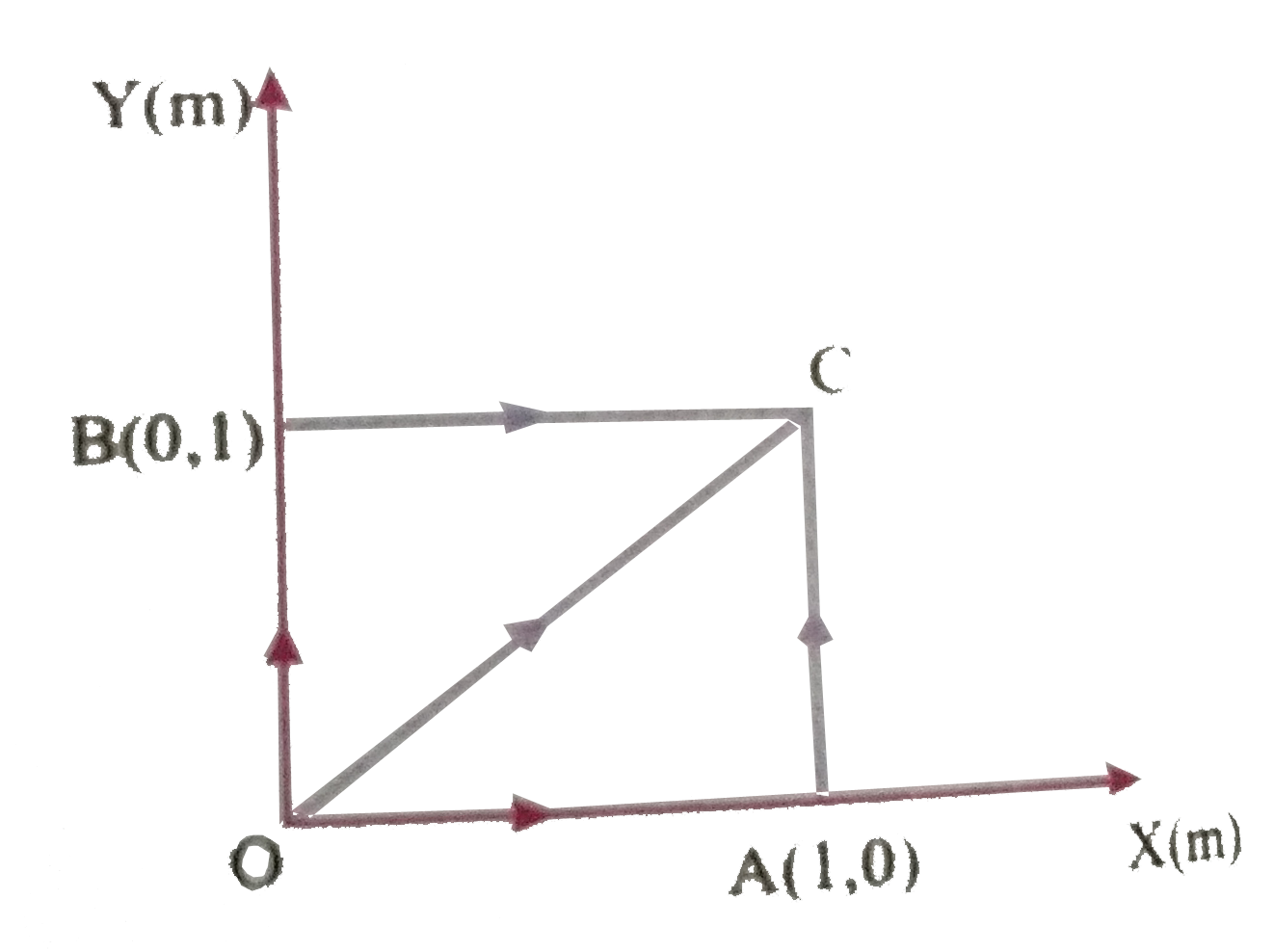
View SolutionOne of the forces acting on a certain particle depends on the particle's position in the `xy`-plane. This force `vec F` expressed in newtons, is given by the expression `vec F = (xy hat i+ xy hat j)` where `x` and `y` are in metres. The particle is moved from `O` to `C` through three different paths :-
The work done by this force on path `OBC` is
View SolutionOne of the forces acting on a certain particle depends on the particle's position in the `xy`-plane. This force `vec F` expressed in newtons, is given by the expression `vec F = (xy hat i+ xy hat j)` where `x` and `y` are in metres. The particle is moved from `O` to `C` through three different paths :-
Which of the following can be negative ?
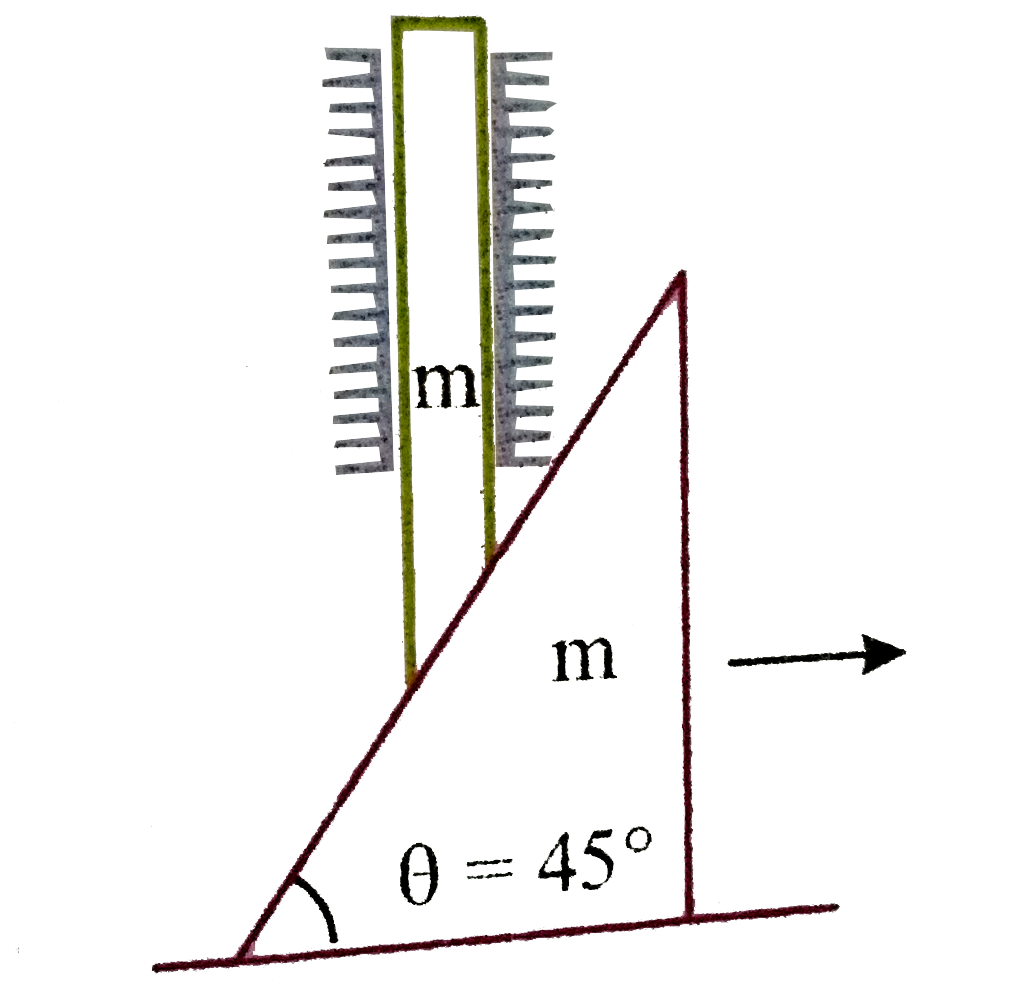
View SolutionA smooth vertical rod is released from rest such that it is constrained to move vertically on a smooth wedge `(theta = 45^@)`. When the wedge moves through a distance `x`, the speed of the rod is :
 .
.
View SolutionThe work done by the normal reaction on the rod is :
View SolutionThe work done by the normal reaction on the wedge is :
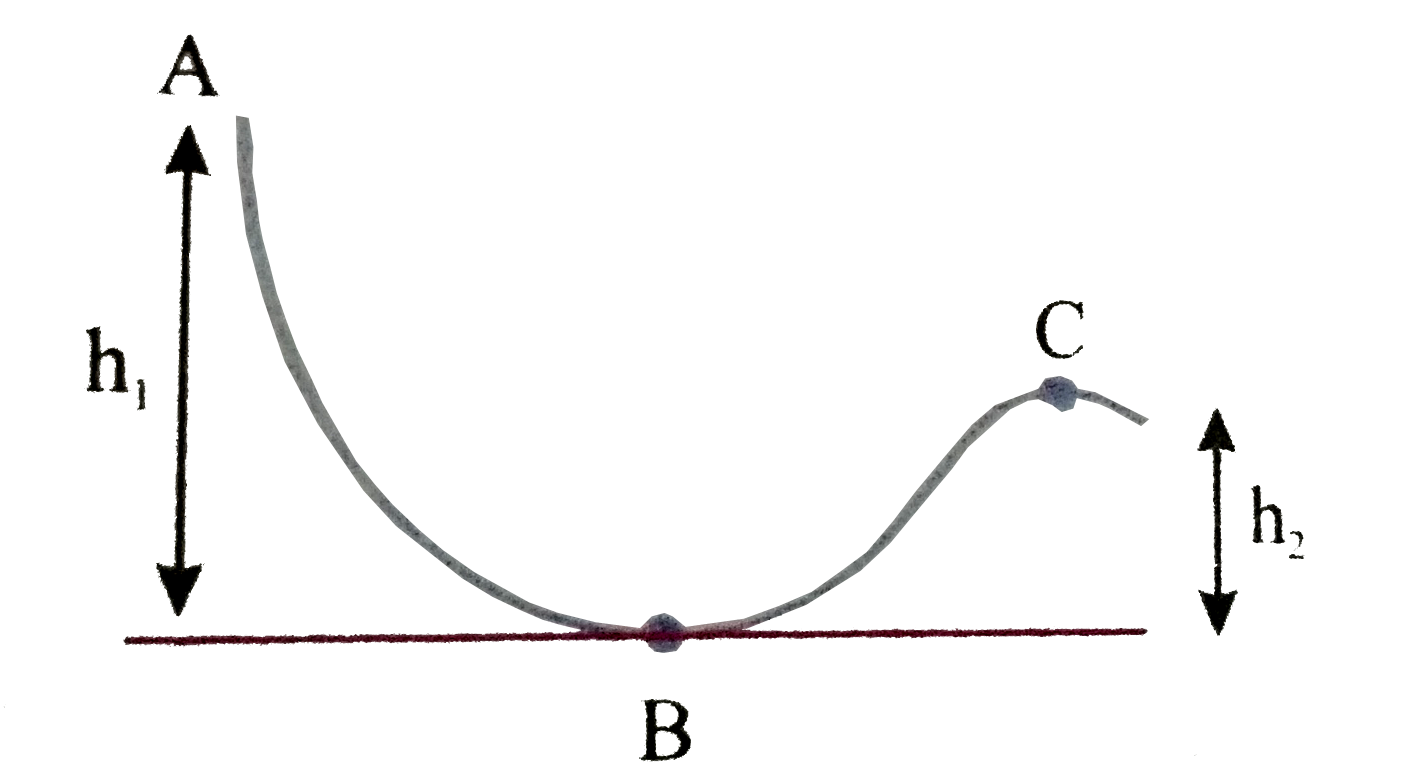
View SolutionA block of mass `m = 1 kg` is released from point `A` along a smooth track as shown. Part `AB` is circular with radius `r_(1) = 4 m` and circular at `C` with radius `r_(2)`. Height of point `A` is `h_(1) = 2m` and of `c` is `h_(2) = 1m (g = 10 m//s^(2))`.
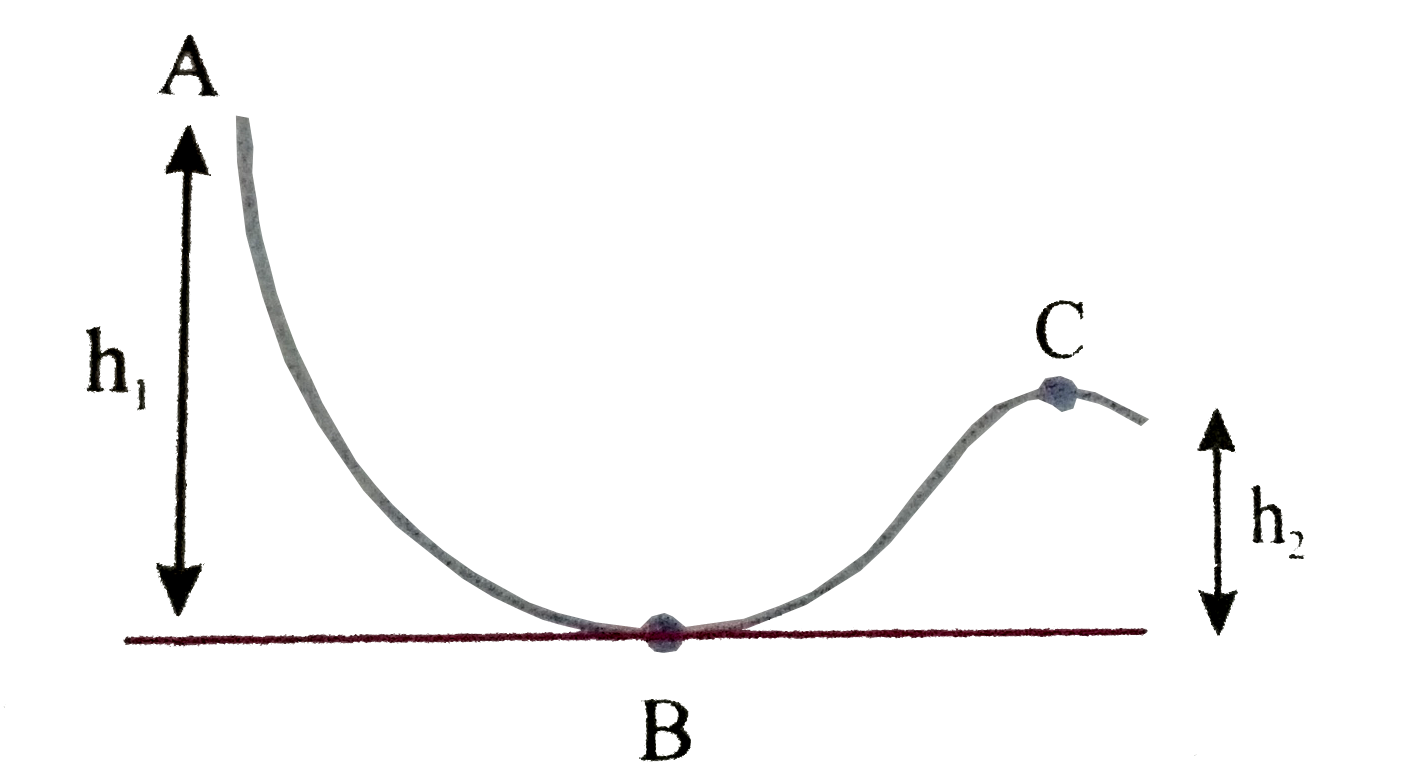 .
.
The force exerted by block on the track at `B` is
View SolutionA block of mass `m = 1 kg` is released from point `A` along a smooth track as shown. Part `AB` is circular with radius `r_(1) = 4 m` and circular at `C` with radius `r_(2)`. Height of point `A` is `h_(1) = 2m` and of `c` is `h_(2) = 1m (g = 10 m//s^(2))`.
 .
.
The minimum safe value of `r_(2)` so that the block does not fly off the track at `C` is
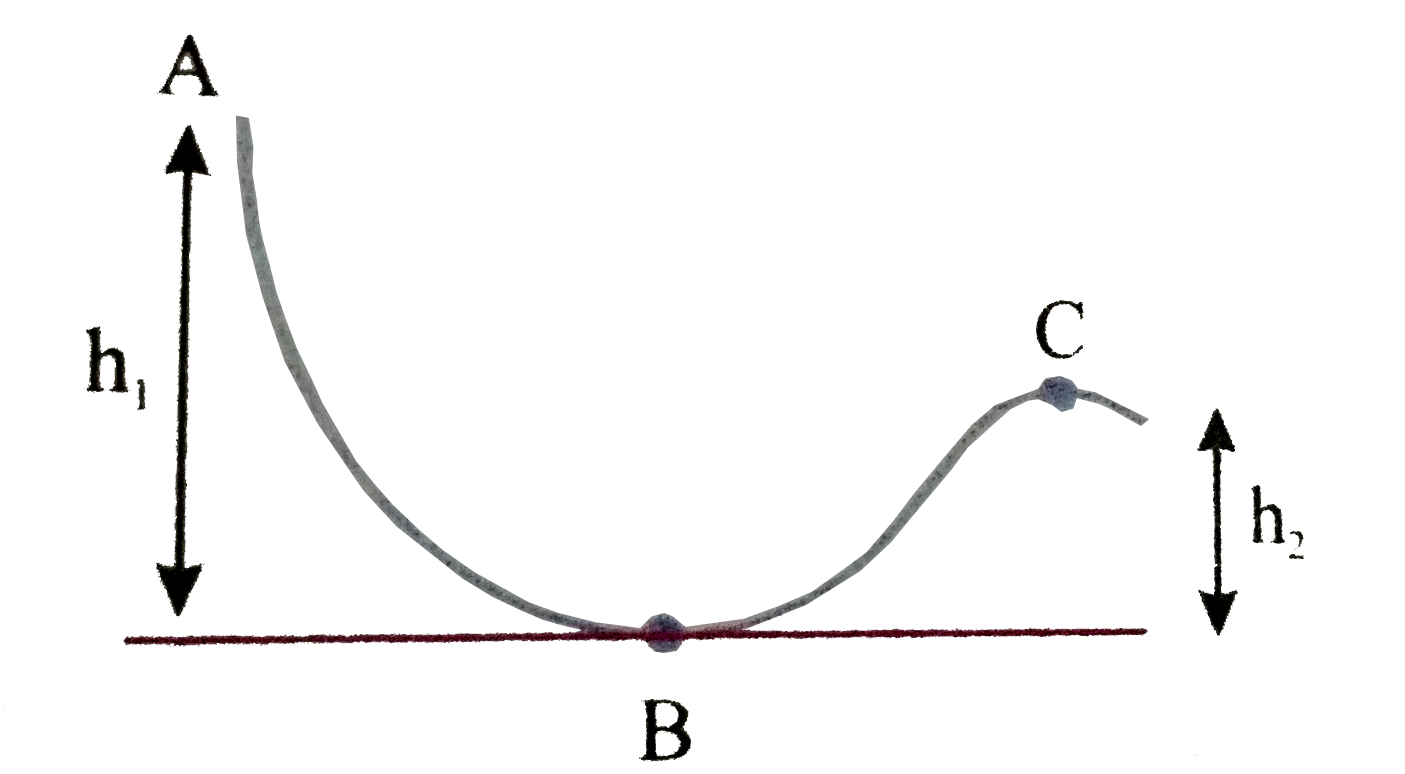
View SolutionA block of mass `m = 1 kg` is released from point `A` along a smooth track as shown. Part `AB` is circular with radius `r_(1) = 4 m` and circular at `C` with radius `r_(2)`. Height of point `A` is `h_(1) = 2m` and of `c` is `h_(2) = 1m (g = 10 m//s^(2))`.
 .
.
The work done by gravitational force from `A` to `C` is
View SolutionA chain of length `l = pi R//4` is placed. On a smooth hemispherical surface of radius `R` with one of its ends fixed at the top of the sphere. Mass of chain is `sqrt(pi kg)` and `R = 1m.(g = 10 m//s^(2))`.
The gravitational potential energy of the chain considering reference level at the base of hemisphere is
View SolutionA chain of length `l = pi R//4` is placed. On a smooth hemispherical surface of radius `R` with one of its ends fixed at the top of the sphere. Mass of chain is `sqrt(pi kg)` and `R = 1m.(g = 10 m//s^(2))`.
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle `theta = (pi)/(4)`.
View SolutionA chain of length `l = pi R//4` is placed. On a smooth hemispherical surface of radius `R` with one of its ends fixed at the top of the sphere. Mass of chain is `sqrt(pi kg)` and `R = 1m.(g = 10 m//s^(2))`.
The tangential acceleration of the chain when its starts sliding down.
View SolutionOne end of a light string of length `L` is connected to a ball and the other end is connected to a fixed point `O`. The ball is released from rest at `t = 0` with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position `A` to `B` is `t_(1)` and from `B` to lowest position `C` is `t_(2)`. Let the velocity of ball at `B` is `vec v_(B)` and at `C` is `vec v_(C)` respectively.
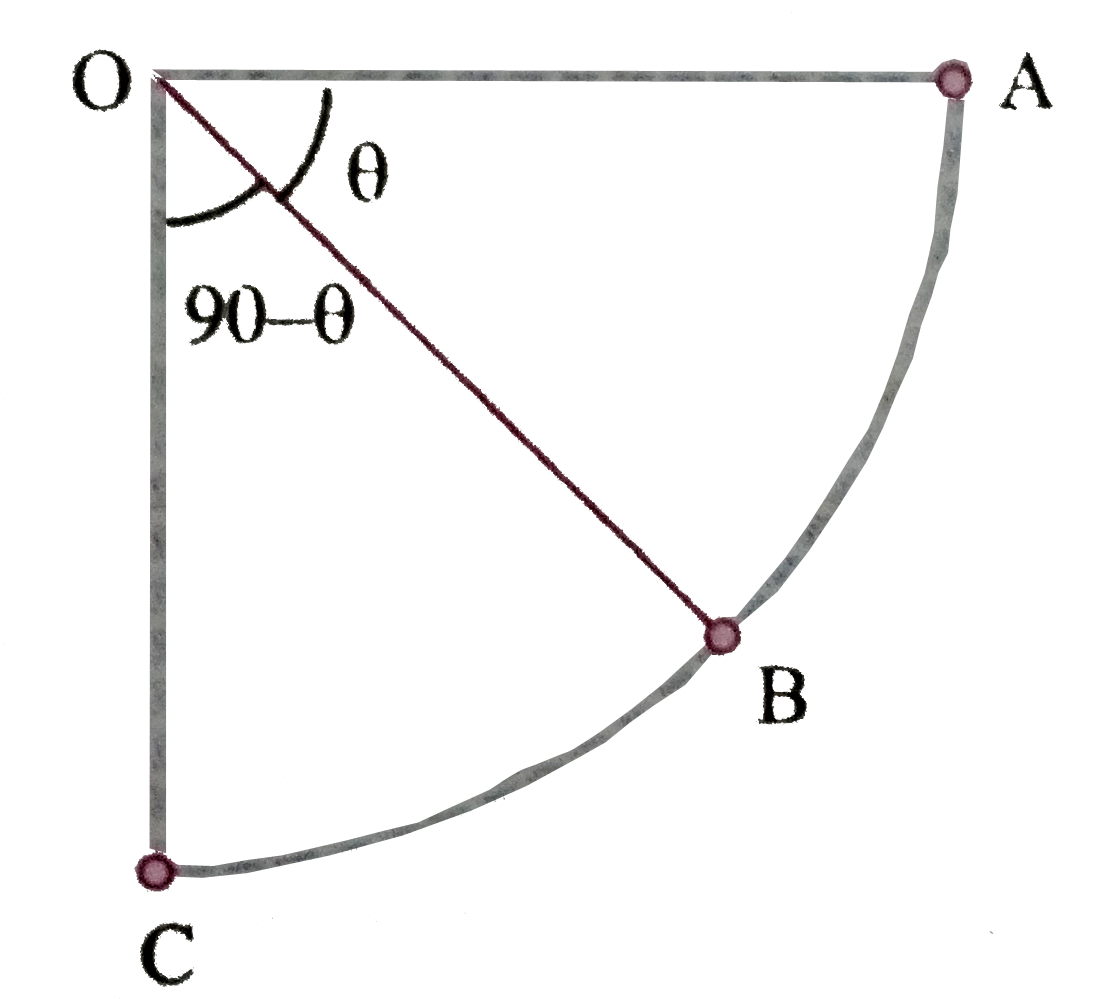
If `|vec v_(C)=2|vecv_(B)|` then the value of `theta` as shown is
View SolutionOne end of a light of length `L` is connected to a ball and other end is connected to a fixed point `O`. The ball is released from rest at `t=0` with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position `A` to `B` is`t_(1)` and from `B` to lowest position `C` is `t_(2)`. Let the velocity of ball at `B` is `vecv_(B)` and at `C` is `vecv_(C)` respectively.

If `|vecv_(c)|=2|vecv_(B)|` then
View SolutionOne end of a light string of length `L` is connected to a ball and the other end is connected to a fixed point `O`. The ball is released from rest at `t = 0` with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position `A` to `B` is `t_(1)` and from `B` to lowest position `C` is `t_(2)`. Let the velocity of ball at `B` is `vec v_(B)` and at `C` is `vec v_(C)` respectively.

If `|vec v_(C)=2|vecv_(B)|` then the value of `theta` as shown is
View Solution
Level-V (Comprehension) questions and complete solutions for chapter WORK POWER AND ENERGY of NARAYANA PHYSICS (HINGLISH) of Class 11