Complete Solutions to Level- III (C.W) of chapter WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK POWER AND ENERGY |
| NARAYANA | Level- III (C.W) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
A long rod `ABC` of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with `A` hinged at the bottom is
 .
.
View SolutionA particle of mass `100 g` is thrown vertically upwards with a speed of `5 m//s`. The work done by the force of gravity during the time the particle goes up is
View SolutionA large slab of mass `5kg` lies on a smooth horizontal surface, with a block of mass `4kg` lying on the top of it. The coefficient of friction between the block and the slab is `0.25`. If the block is pulled horizontally by a force of F `=6N`, the work done by the force of friction on the slab, between the instants `t=2s` and `t=3s`, is `(g=10ms^-2)`

View SolutionIn the pulley-block system shown in figure, strings are light. Pulleys are massless and smooth. System is released from rest. In `0.3` seconds.
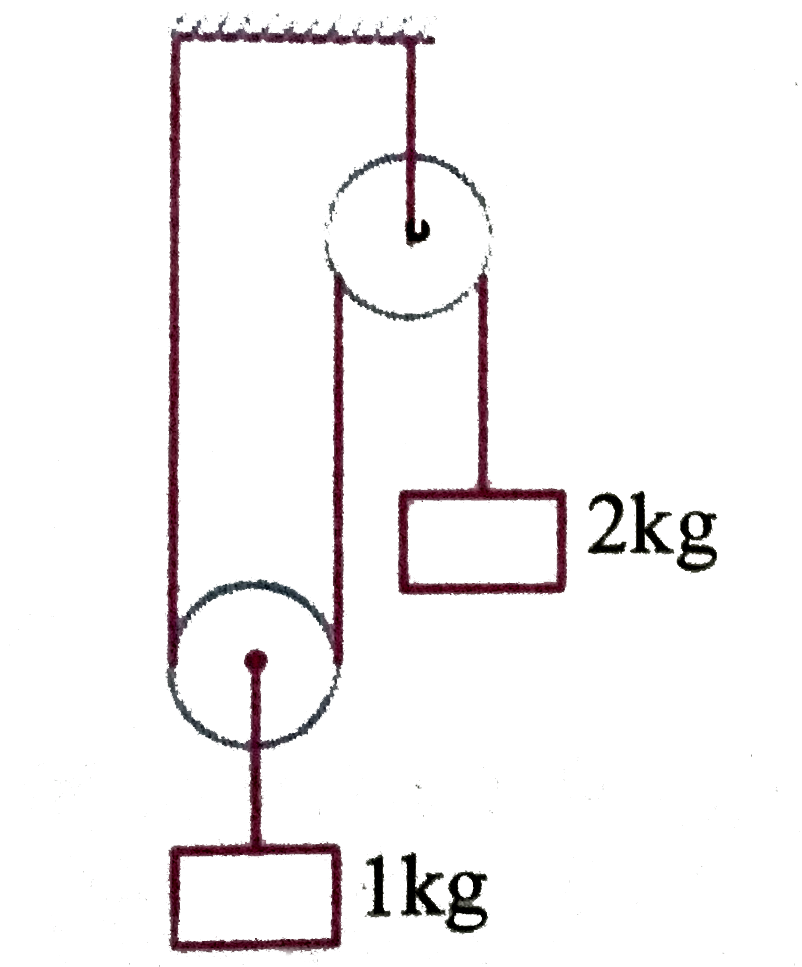 .
.
(a) work done on `2 kg` block by gravity is `6 J`
(b) work done one `2 kg` block by string is `-2 J`
( c) work done on `1 kg` block by gravity is `-1.5 J`
(d) work done on `1 kg` block string is `2 J`.
View SolutionA particle of mass `0.5kg` travels in a straight line with velocity `v=ax^(3//2)` where `a=5m^(-1//2)s^-1`. What is the work done by the net force during its displacement from `x=0` to `x=2m`?
View SolutionA particle of mass `2 kg` starts moving in a straight line with an initial velocity of `2 m//s` at a constant acceleration of `2 m//s^(2)`. Then rate of change of kinetic energy.
View SolutionA running man has half the KE that a body of half his mass has. The man speeds up by `1.0ms^(-1)` and then has the same energy as the boy. What were the original speeds of the man and the boy?
View SolutionThe kinetic energy `(KE)` versus time graph for a graph for a particle moving along a straight line is shown in the figure. The force `vs` time graph for the particle may be
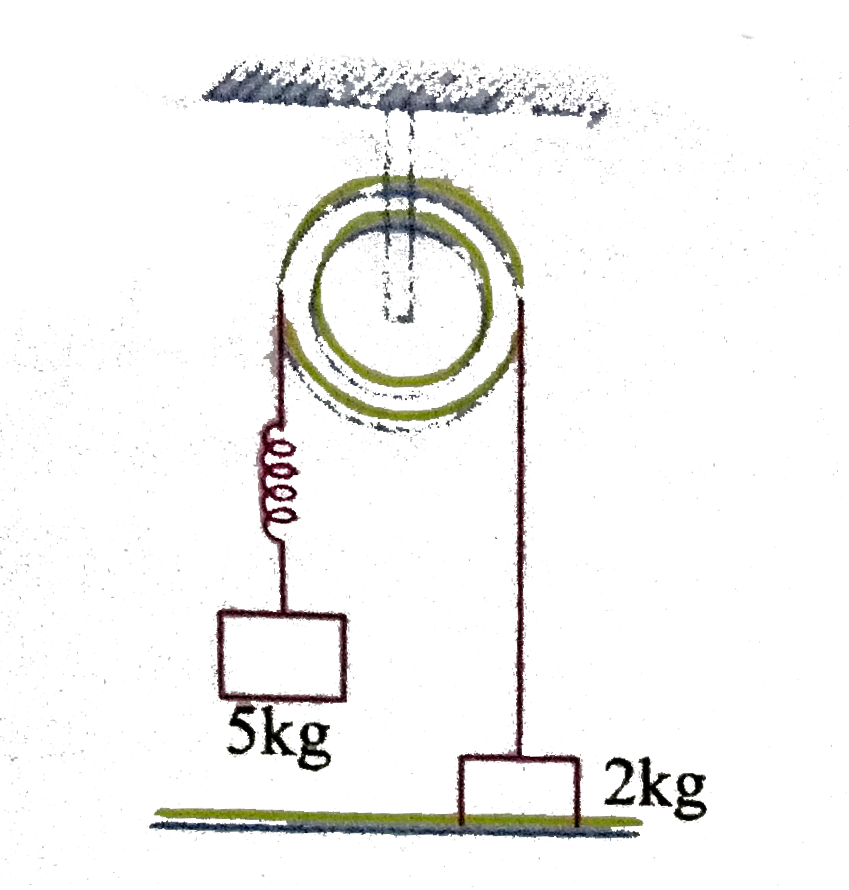 .
.
View SolutionA lifting machine, having an efficiency of `80 %` uses `2500 J` of energy in lifting a `10 kg` load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be `(g =10 m//s^(2))`
View SolutionA chain (AB) of length `l` loaded in a smooth horizontal table so that its fraction of length h hangs freely and touches the surface of the table with its end B. At a certain moment ,the end A of the chain is set free. With what velocity will this end the chain slip out of the table ?
 .
.
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionA `1.5 kg` block is initially at rest on a horizontal frictionless surface. A horizontal force `vec F=(4-x^(2))hat i` is applied on the block. Initial position of the block is at `x = 0`. The maximum kinetic enery of the block between `x = 0` and `x = 2m` is
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates `5%` of its initial energy against air resistance ?
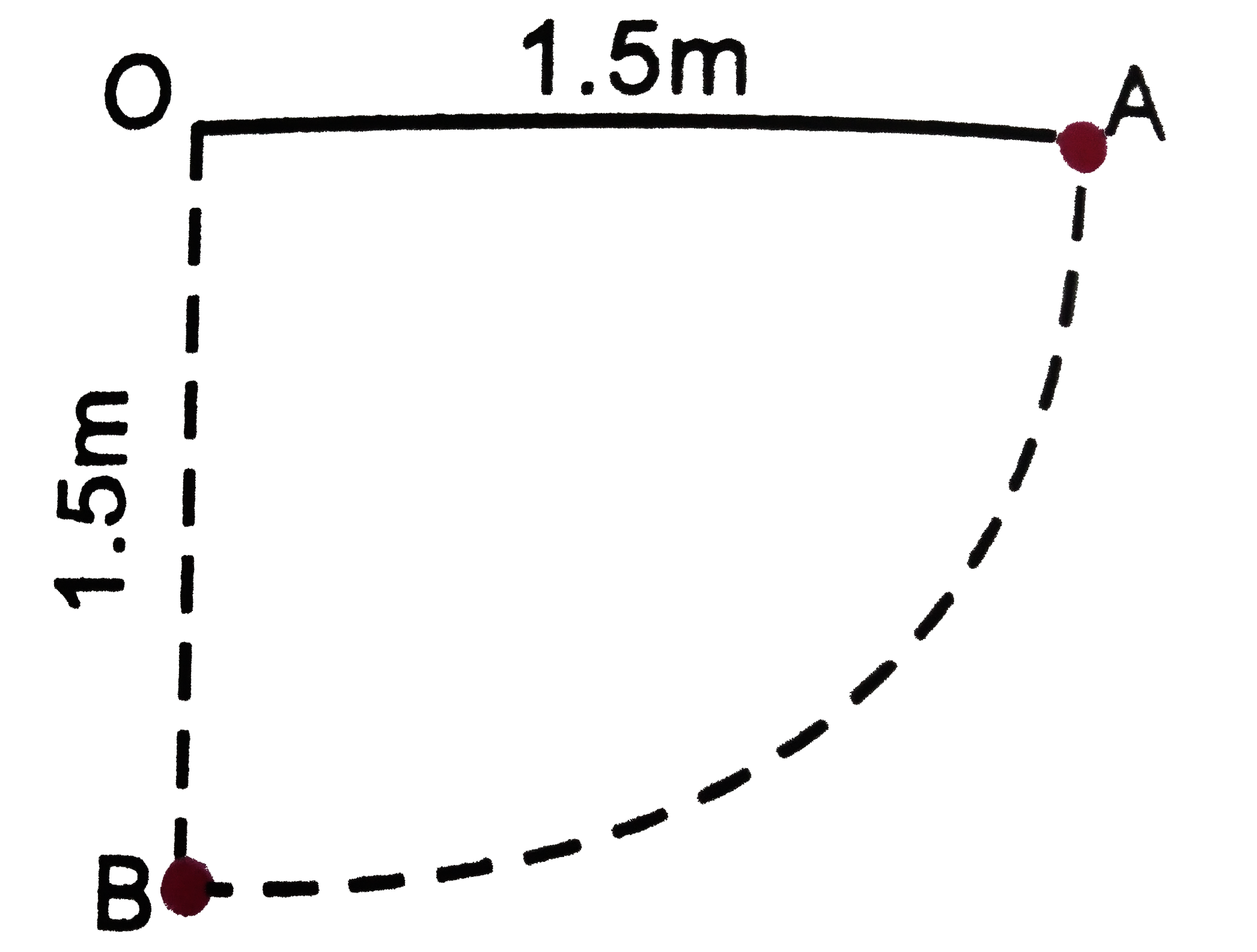
View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of `5 kg` block when `2 kg` block leaves the constant of with ground is (force constant of spring `k = 40 N//m and g = 10 m//s^(2))`

View SolutionThe potential energy of a particle of mass `m` is given by `U = (1)/(2) kx^(2)` for `x lt 0` and `U=0` for `x ge 0`. If total mechanical energy of the particle is `E`. Then its speed at `x = sqrt((2E)/(k))` is
View SolutionA 1kg block situated on a rough incline is connected to a spring of spring constant `100Nm^(-1)` as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
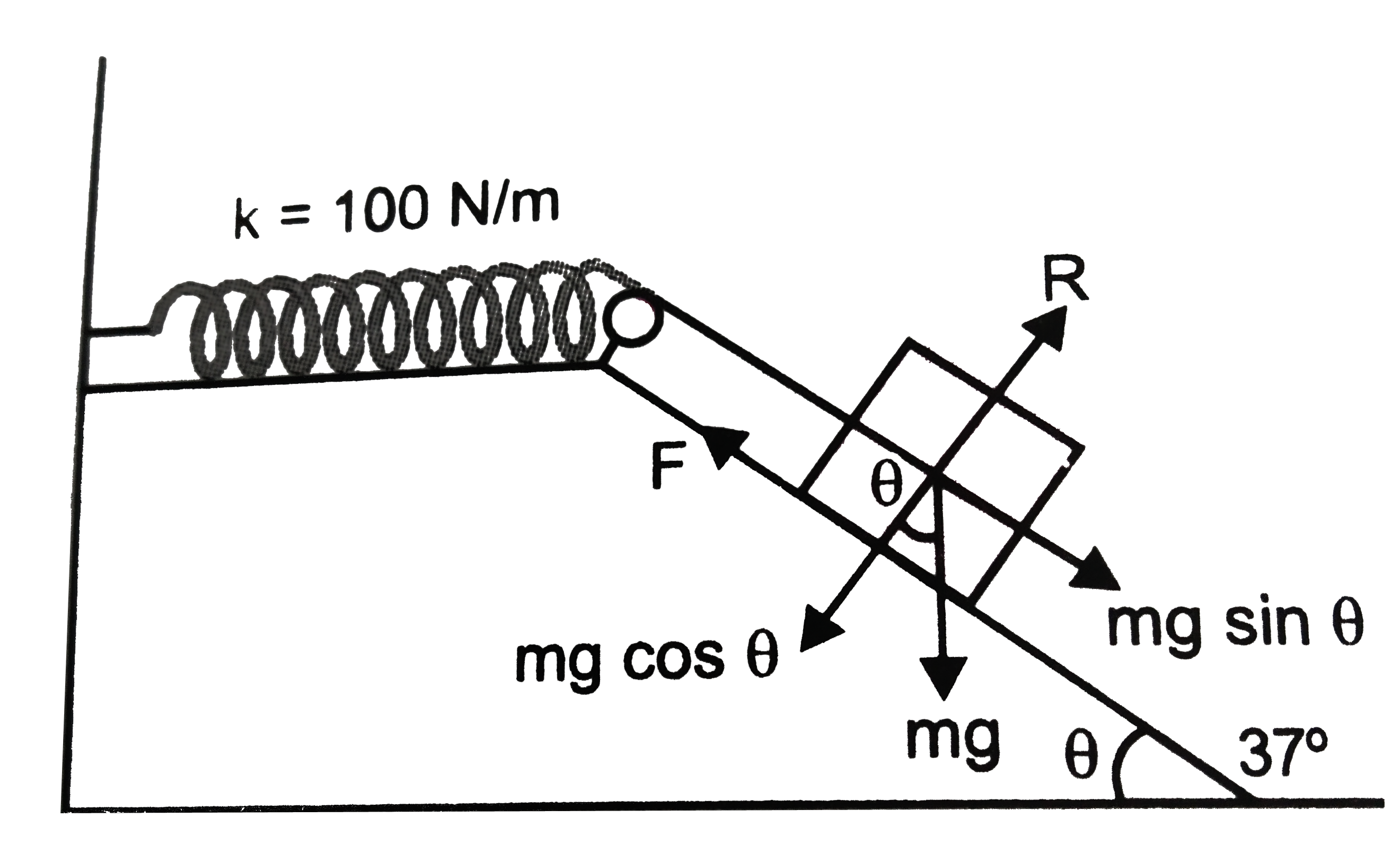
View SolutionA light spring of force constant 'K' is held between two blocks of masses 'm' and '2m'. The two blocks and the spring system rests on a smooth horizontal floor. Now th blocks are moved towards each other compressing the springs by 'x' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be
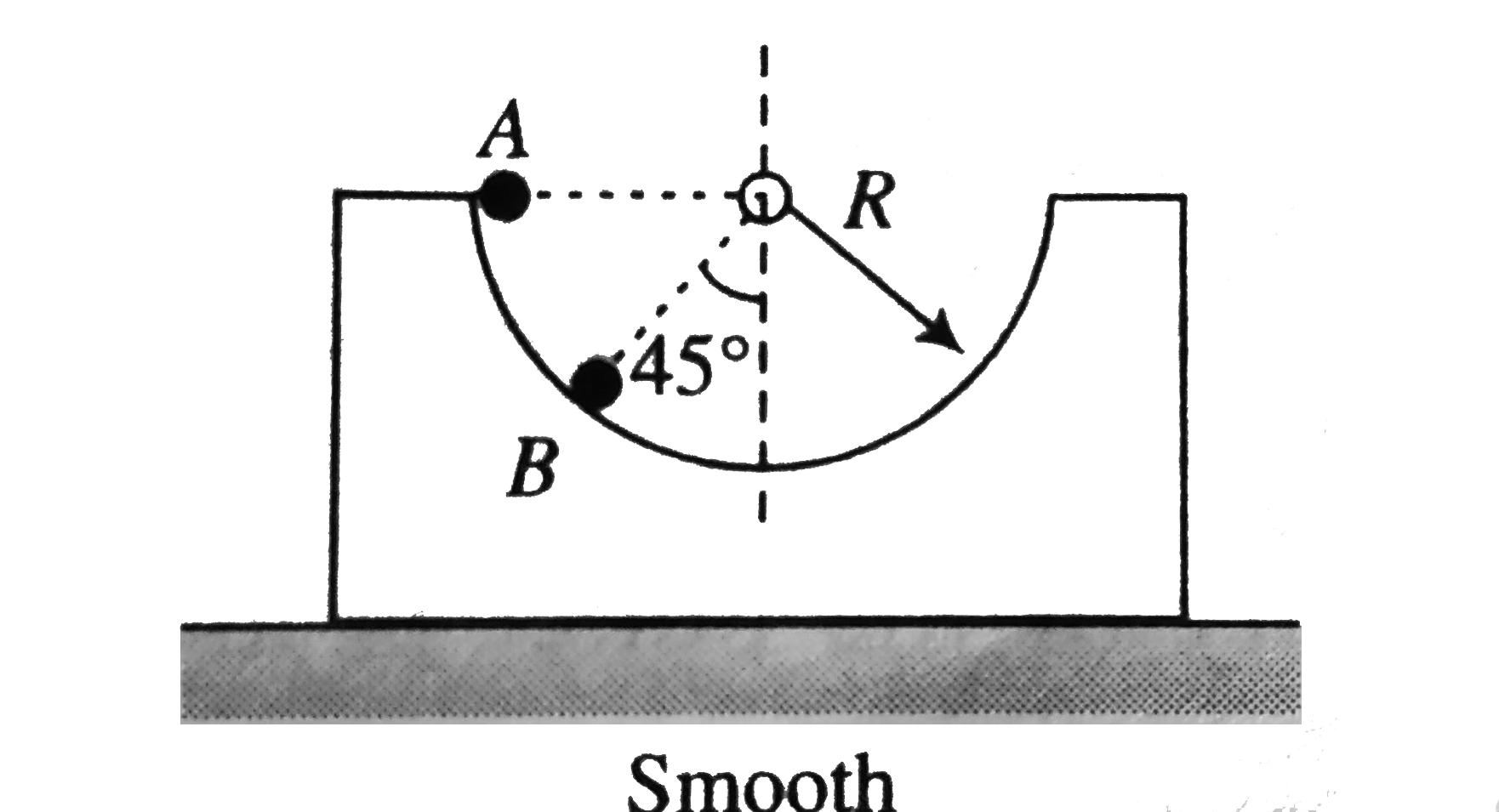
View SolutionA ball of mass `m` is released from A inside a smooth wedge of mass `m` as shown in figure. What is the speed of the wedge when the ball reaches point B?
View SolutionPower supplied to a mass `2 kg` varies with time as `P = (3t^(2))/(2)` watt. Here `t` is in second . If velocity of particle at `t = 0 is v = 0`, the velocity of particle at time `t = 2s` will be:
View SolutionA particle of mass in is moving in a circular with of constant radius `r` such that its contripetal accelenation `a_(c) ` is varying with time `t` as `a_(c) = K^(2) rt^(2)` where K` is a constant . The power delivered to the particles by the force action on it is
View SolutionA constant power `P` is applied to a particle of mass `m`. The distance traveled by the particle when its velocity increases from `v_(1)` to `v_(2)` is (neglect friction):
View SolutionA body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity `(s//v)` varies with time `t` as
View SolutionPower applied to a particle varices with time as `P =(3t^(2)-2t + 1)` watt, where t is in second. Find the change in its kinetic energy between time `t=2s` and `t = 4 s` .
View SolutionA car of mass `M` accelerates starting from rest. Velocity of the car is given by `v=((2Pt)/(M))^((1)/(2))` where `P` is the constant power supplied by the engine. The position of car as a function of time is given as
View SolutionDuring gas of negligible mass is sealed in a test tube of mass `50 gm` with the helo of a stopper of mass `3.5 gm`. The test tube is suspended from a fixed point with help of massless string such that the test tube is horizontal and distance between point of suspension and centre of mass of test tube is `25 cm`. The test tube is heated to a temperature due to which stopper is ejected out horizontally while test tube completes a vertical circle of radius `25 cm`. The minimum velocity with which stopper should be ejected out is
View SolutionA nail is fixed at a point `P` vertically below the point of suspension 'O' of simple pendulum of length `1 m`. The bob is released when the string of pendulum makes an angle `30^@` with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with `P` . The least distance of `P` from `O` is
View SolutionA simple pendulum with a bob of mass 'm' swings with angular amplitude of `60^@`. When its angular displacement is `30^@`, the tension in the strings would be
View SolutionA block is freely sliding down from a vertical height `4 m` on smooth inclined plane. The block reaches bottom of inclined plane and then it decribes vertical circle of radius `1 m` along smooth track. The ratio of normal reactions on the block while it crossing lowest point and highest point of vertical circle is
View SolutionThe length of a ballistic pendulum is `1 m` and mass of its block is `1.9 kg`. A bullet of mass `0.1 kg` strikes the block in horizontal direction with a velocity `100 ms^(-1)` and got embedded in the block. After collision the combined mass swings away from lowest point. The tension in the strings when it makes an angle `60^@` with vertical is `(g=10 ms^(-2))`.
View SolutionA stone attached to a string is rotated in a vertical circle such that when it is at the top of the circle its speed is `V` and there is neither tension nor slacking in the string. The speed of stone when its angular displacement is `120^@` from the lowest point is
View SolutionMass of the bob of a simple pendulum of length `L` is `m`. If the bob is projected horizontally from its mean position with velocity `sqrt(4 gL)`, then the tension in the string becomes zero after a vertical displacement of
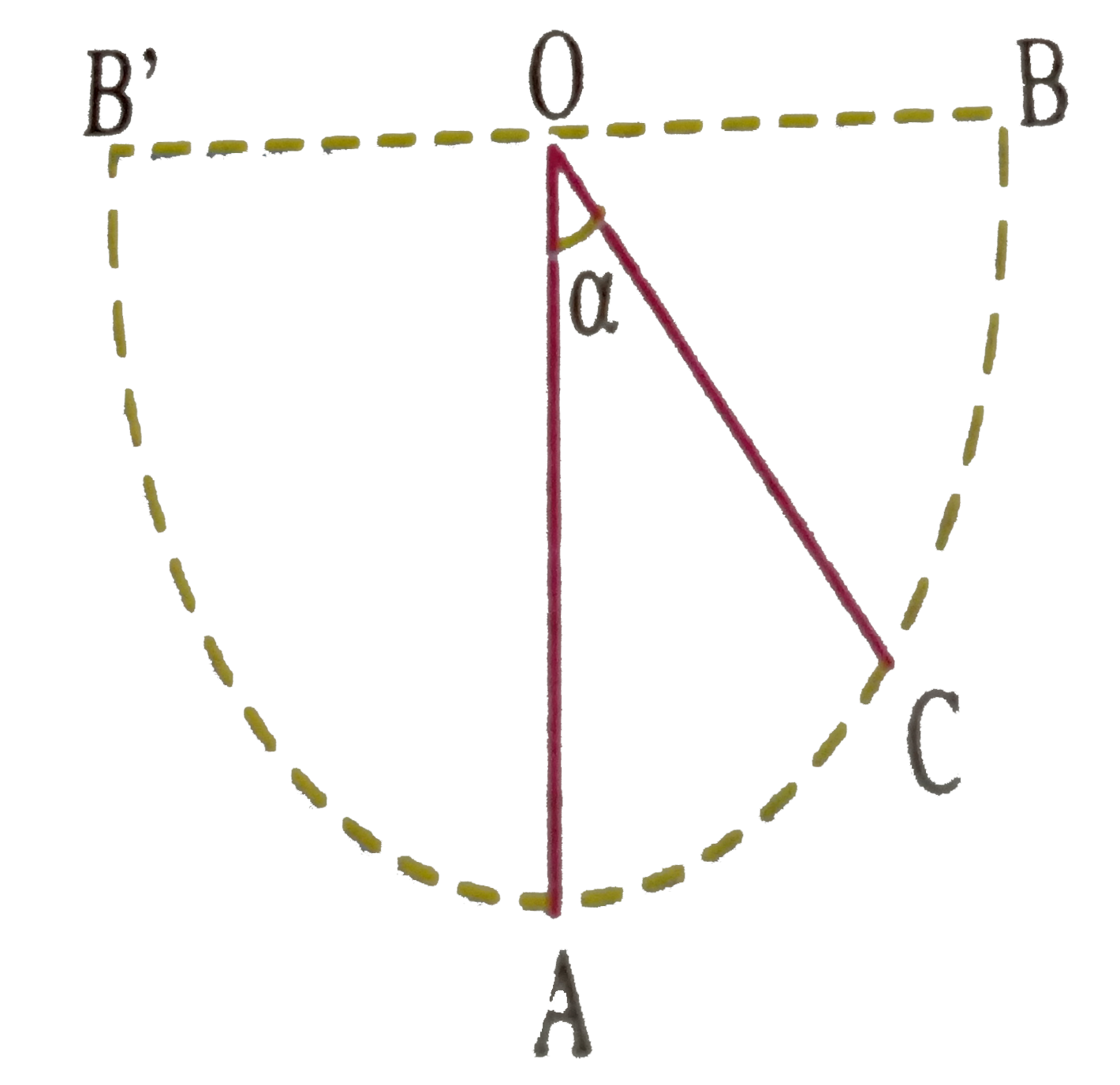
View SolutionA bob of mas `M` is suspended by a massless string of length `L`. The horizontal velocity `v` at position `A` is just sufficient to make it reach the point `B`. The angle `theta` at which the speed of the bob is half of that at `A`, satisfies.
 .
.
View SolutionA simple pendulum is oscillating with an angular amplitude of `90^(@)` as shown in the figure. The value of `theta` for which the resulting acceleration of the bob is directed (i) vertically downward, (ii) vertically upward and (iii) horizontally is`

View SolutionA block of wood of mass `3M` is suspended by a string of length `(10)/(3) m`. A bullet of mass `M` hits it with a certain velocity and gets embedded in it. The block and the bullet swing to one side till the string makes `120^@` with the initial position. the velocity of the bullet is `(g=10 ms^(-2))`.
View SolutionA wooden block of mass `10 gm` is dropped from the top of a cliff `100 m` high. Simultaneously a bullet of same mass is fired from the foot of the cliff vertically upwards with a velocity of `100 ms^(-1)`. If the bullet after collision gets embedded in the block, the common velocity of the bullet and the block immediately after collision is `(g=10 ms^(-2))`.
View SolutionA particle of mass `m` has a velocity `-v_(0) i`, while a second particle of same mass has a velocity `v_(0) j`. After the particles collide, first particle is found to have a velocity `(-1)/(2) v_(0) overline i` then the velocity of othe particle is
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of `10 m//s`. Time taken by the two radius vectors connecting of explosion to fragments to make `90^(@)` is
View SolutionA test tube of mass `20 gm` is filled with a gas and fitted with a stopper of `2 gm`. It is suspended horizontally by means of a thread of `1m` length and heated. When the stopper kicks out, the tube just completes a circle in vertical plane. The velocity with which the stopper kicked out is
View SolutionTwo bodies move towards each other and collide inelastically. The velocity of the first body is `2 m//s` and that of the seconf is `4m//sec` before impact. The common velocity after collision is `1 m//s` in the direction of the first body. The number of times did the `KE` of the first body exceed that of the second body before collision.
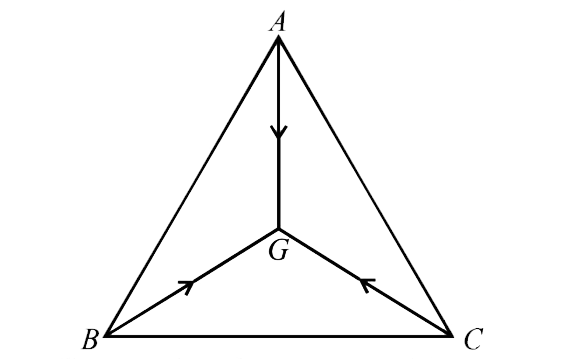
View SolutionThree particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
View SolutionA moving sphere `P` collides another sphere `Q` at rest. If the collision takes place along the line joining their centers of mass such that their total kinetic enegry is conserved and the fraction of `K.E` transferred by the colliding particle is `(8)/(9)`, then the mass of `P` and mass of `Q` bears a ratio
View SolutionA particle strikes a horizontal frictionless floor with a speed 'u' at an angle 'theta' with the vertical and rebounds with a speed 'v' at an angle 'alpha' with the vertical. Find the value of 'v' if 'e' is the coefficient of restitution.
View SolutionTwo sphere `A` and `B` of equal masses lie on the smooth horizontal circular groove at opposite ends of diameter and at the end of time 't','A' impings on 'B' . If 'e' is the coefficient of restitution, the second impinge will occur after a time
View SolutionA ball is thrown at an angle of incidence `'theta'` on a horizontal plane such that the incident direction and the reflected direction are at right angle to each other. If the coefficient of restuitution is `'e'` then `'theta'` is equal to
View SolutionConsider the collision depicted in Figure, to be between two billiard balls with equal masses `m_(1)=m_(2)`. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle `theta_(2)=phi=37^(@)`. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain `theta_(1)=theta` .
View SolutionA projectile is fixed on a horizontal ground. Coefficient of restitution between the projectile and the ground is 'e'. If `a,b` and `c` be the ration of time of flight `[(T_(1))/(T_(2))]`, maximum height `[(H_(1))/(H_(2))]` and horizontal range `[(R_(1))/(R_(2))]` in first two collisions with the ground, then
View SolutionA wall moving with velocity `2 cms^(-1)` towards the ball and ball is moving towards the wall with a velocity `10 cms^(-1)`. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in `cms^(-1)`.
View SolutionA body A moves towards a wall with velocity `V`. The wall also moves towards the body `A` with velocity `V_(0)`. After collision the body moves in opposite direction with velocity `V^(|)` which is `(1+(2V_(0))/(V))` times the velocity `V`. The coefficient of restitution is
View SolutionA sphere `A` of mass `m` moving with a velocity hits another stationary sphere `B` of same mass. If the ratio of the velocity of the sphere after collision is `(v_(A))/(v_(B)) = (1 - e)/(1 + e)` where `e` is the coefficient of restitution, what is the initial
velocity of sphere `A` with which it strikes?
View SolutionA ball `A` of mass `3 m` is placed at a distance `d` from the wall on a smooth horizontal surface Another ball `B` of mass `m` moving with velocity `u` collides with ball `A`. The coefficient of restitution between the balls and the wall and between the balls is `e`
(a) the velocity of ball `B` after collision is `(u(3e-1))/(4)`.
(b) the velocity of ball `B` after collision is `(u(2e-1))/(4)`.
( c) after collision, ball `A` will have away by distance `(d(2e-1))/((2e-1))` during the time ball `B` returns back to wall.
(d) after collision, ball `A` will move away by distance `(d(e-1))/((3e-1))` during the time ball `B` returns back to wall.
View Solution
Level- III (C.W) questions and complete solutions for chapter WORK POWER AND ENERGY of NARAYANA PHYSICS (HINGLISH) of Class 11