Complete Solutions to Level-VI (Comprehension) of chapter WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK POWER AND ENERGY |
| NARAYANA | Level-VI (Comprehension) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
The potential energy `U`(in `J`) of a particle is given by `(ax + by)`, where `a` and `b` are constants. The mass of the particle is `1 kg` and `x` and `y` are the coordinates of the particle in metre. The particle is at rest at `(4a, 2b)` at time `t = 0`.
Find the speed of the particle when it crosses x-axis
View SolutionThe potential energy `U`(in `J`) of a particle is given by `(ax + by)`, where `a` and `b` are constants. The mass of the particle is `1 kg` and `x` and `y` are the coordinates of the particle in metre. The particle is at rest at `(4a, 2b)` at time `t = 0`.
Find the speed of the particle when it crosses y-axis.
View SolutionThe potential energy `U`(in `J`) of a particle is given by `(ax + by)`, where `a` and `b` are constants. The mass of the particle is `1 kg` and `x` and `y` are the coordinates of the particle in metre. The particle is at rest at `(4a, 2b)` at time `t = 0`.
Find the acceleration of the particle.
View SolutionThe potential energy `U`(in `J`) of a particle is given by `(ax + by)`, where `a` and `b` are constants. The mass of the particle is `1 kg` and `x` and `y` are the coordinates of the particle in metre. The particle is at rest at `(4a, 2b)` at time `t = 0`.
Find the coordinates of the particle at `t =1` second.
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
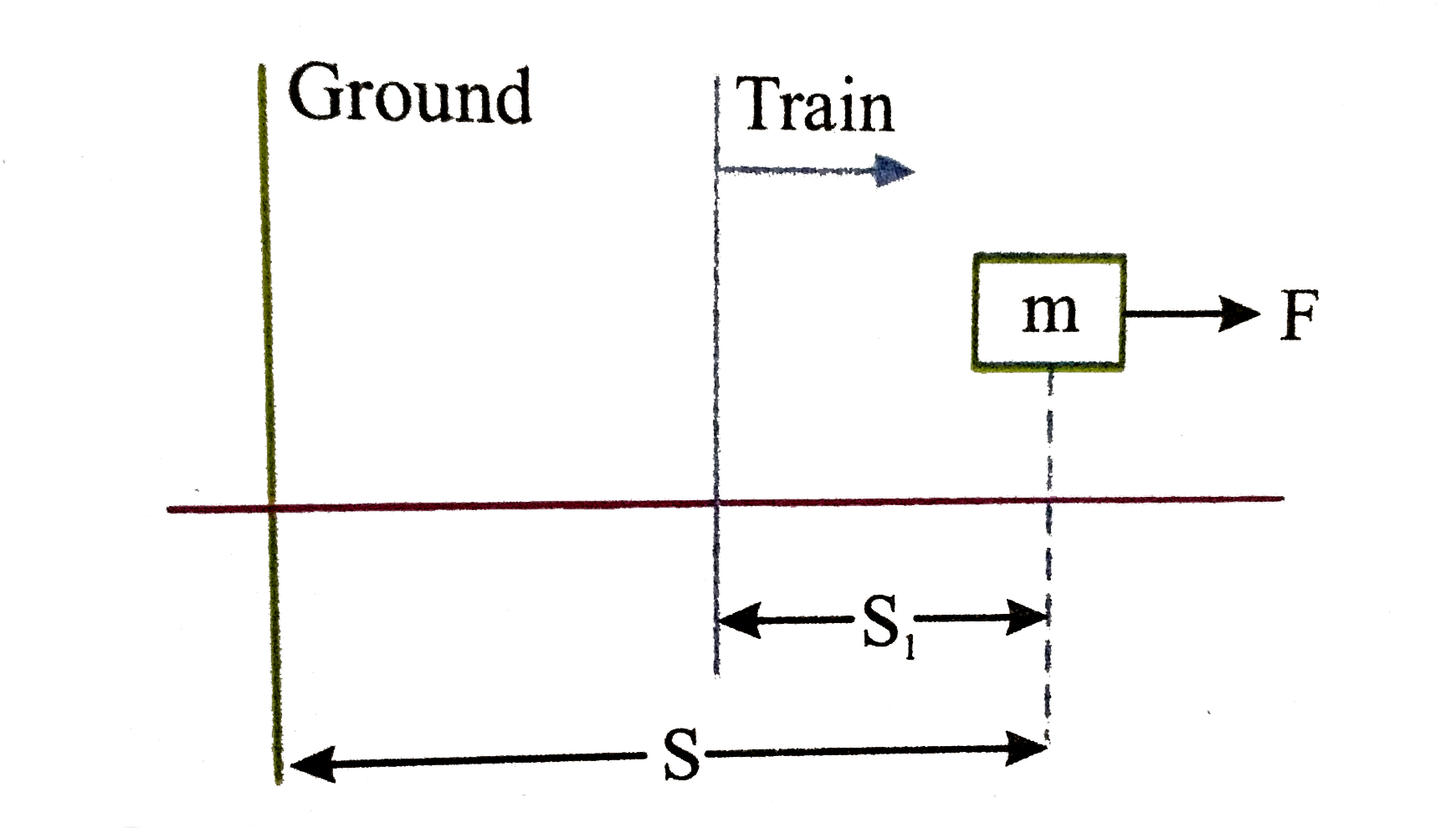
What is the final speed of the block according to a person in the car ?
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
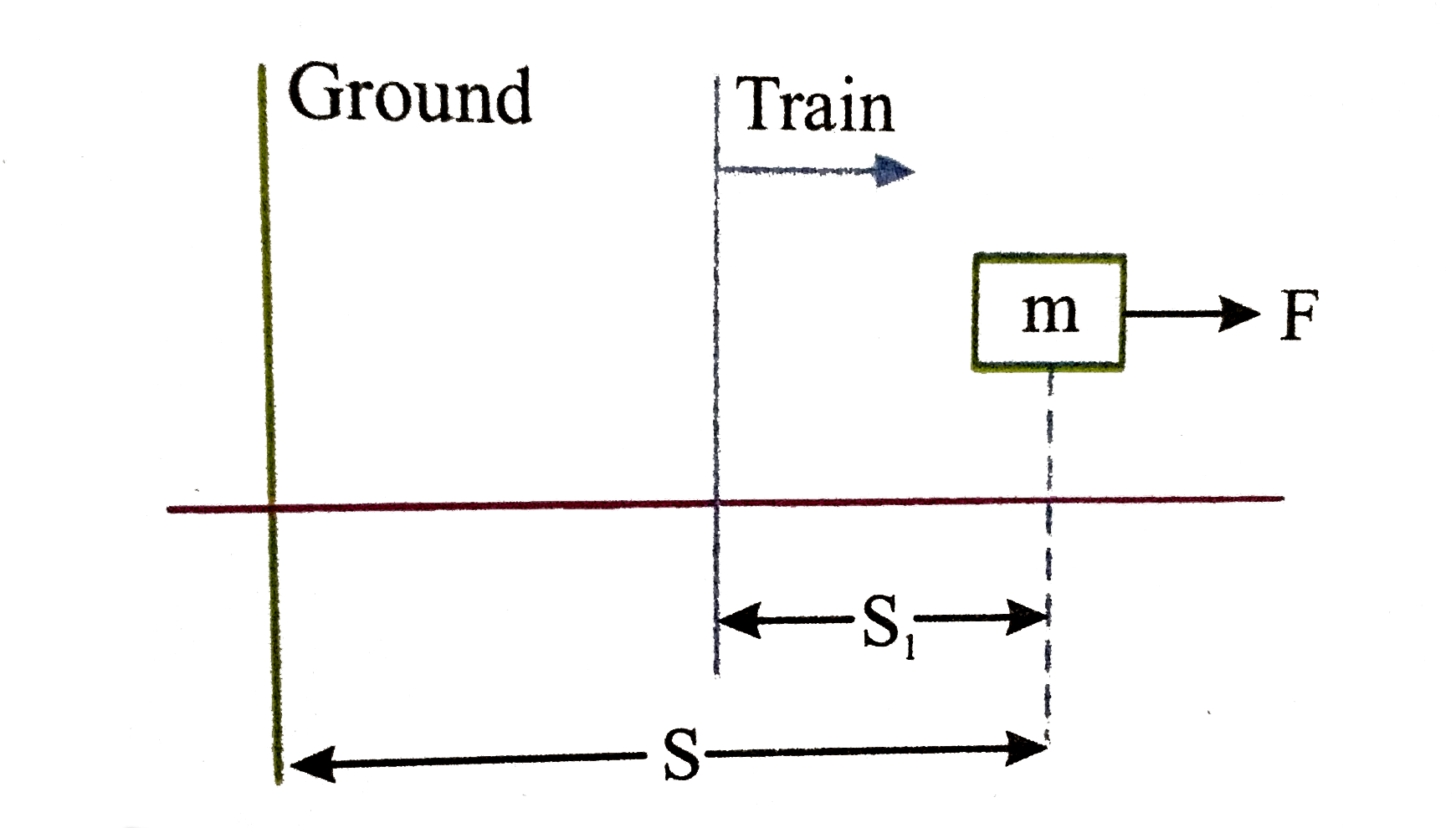
According to a person standing on the ground outside the train ?
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
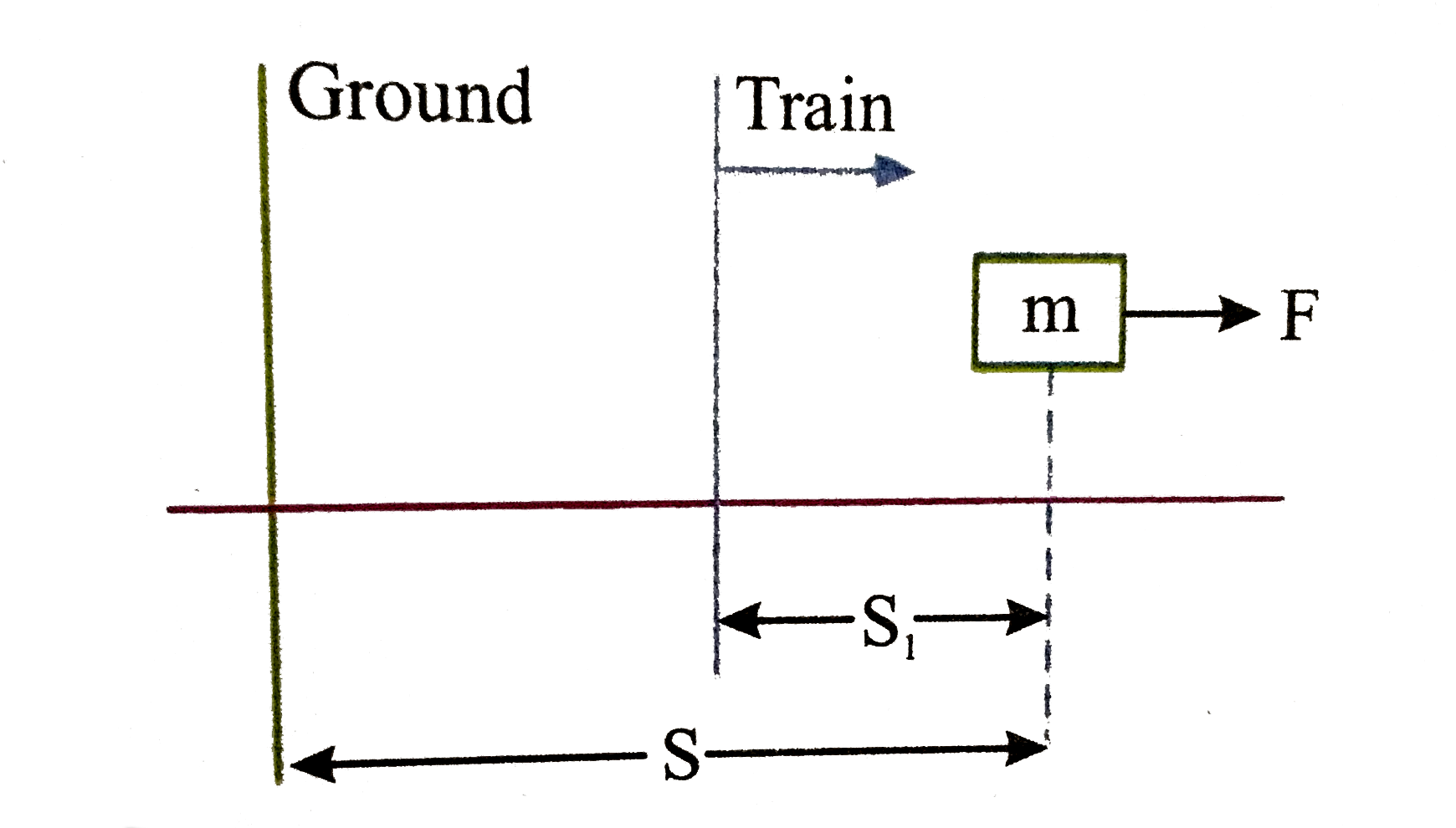
How much did `K.E` of the block change according to the person in the car ?
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
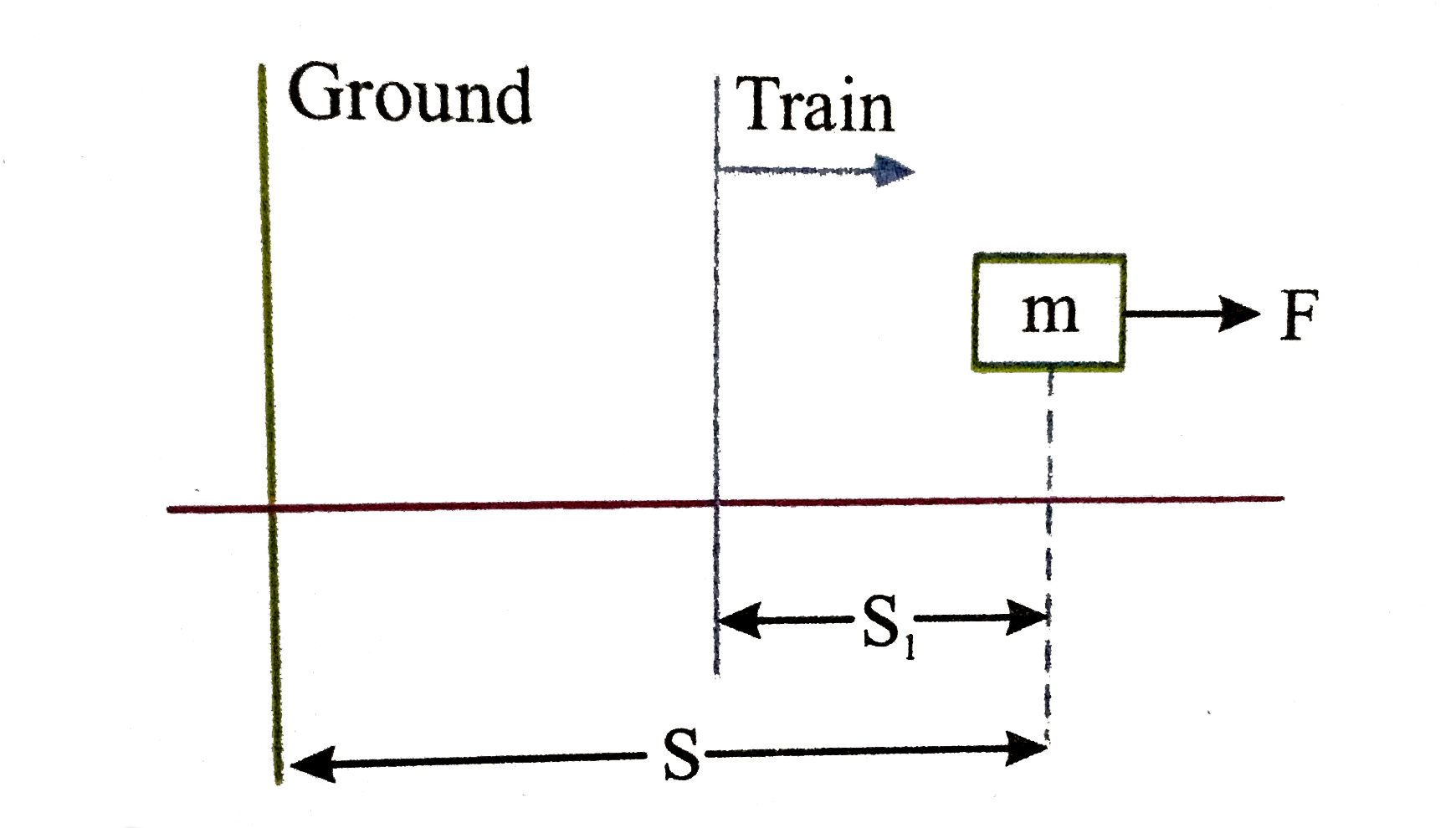
According to the person on the ground. The change in `KE` of block is
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
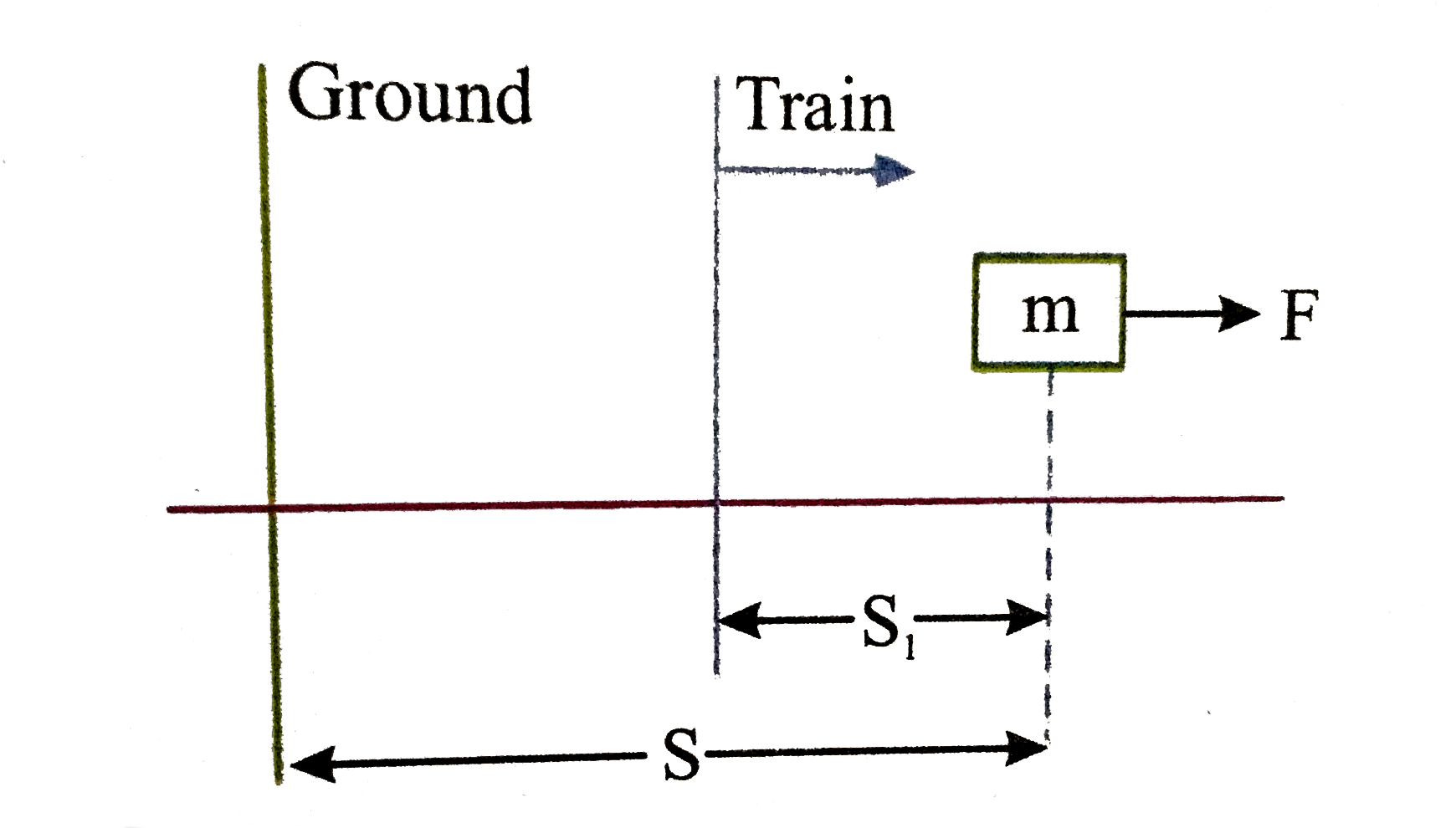
In terms of `F,m` & `t`, how far did the the force displace the object according to the person in car ?
View SolutionA block of mass `m` sits at rest on a frictionless table in a rail car that is moving with speed `v_(c)` along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force `F` for a time `t` in the direction of the car's motion.
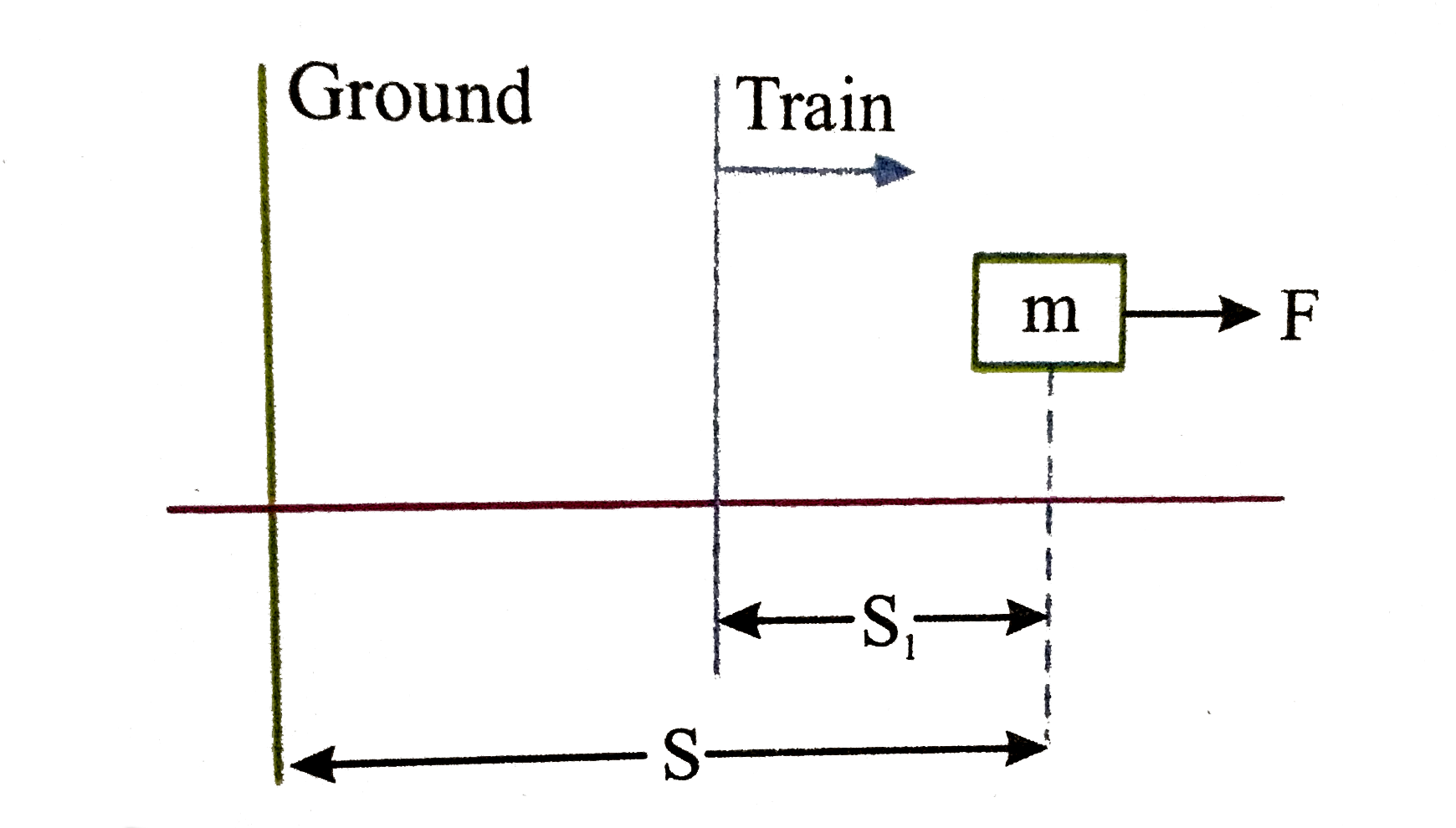
According to the person on the ground. The displacement of block is
View SolutionIn the figure the variation of potential energy of a particle of mass `m = 2kg` is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
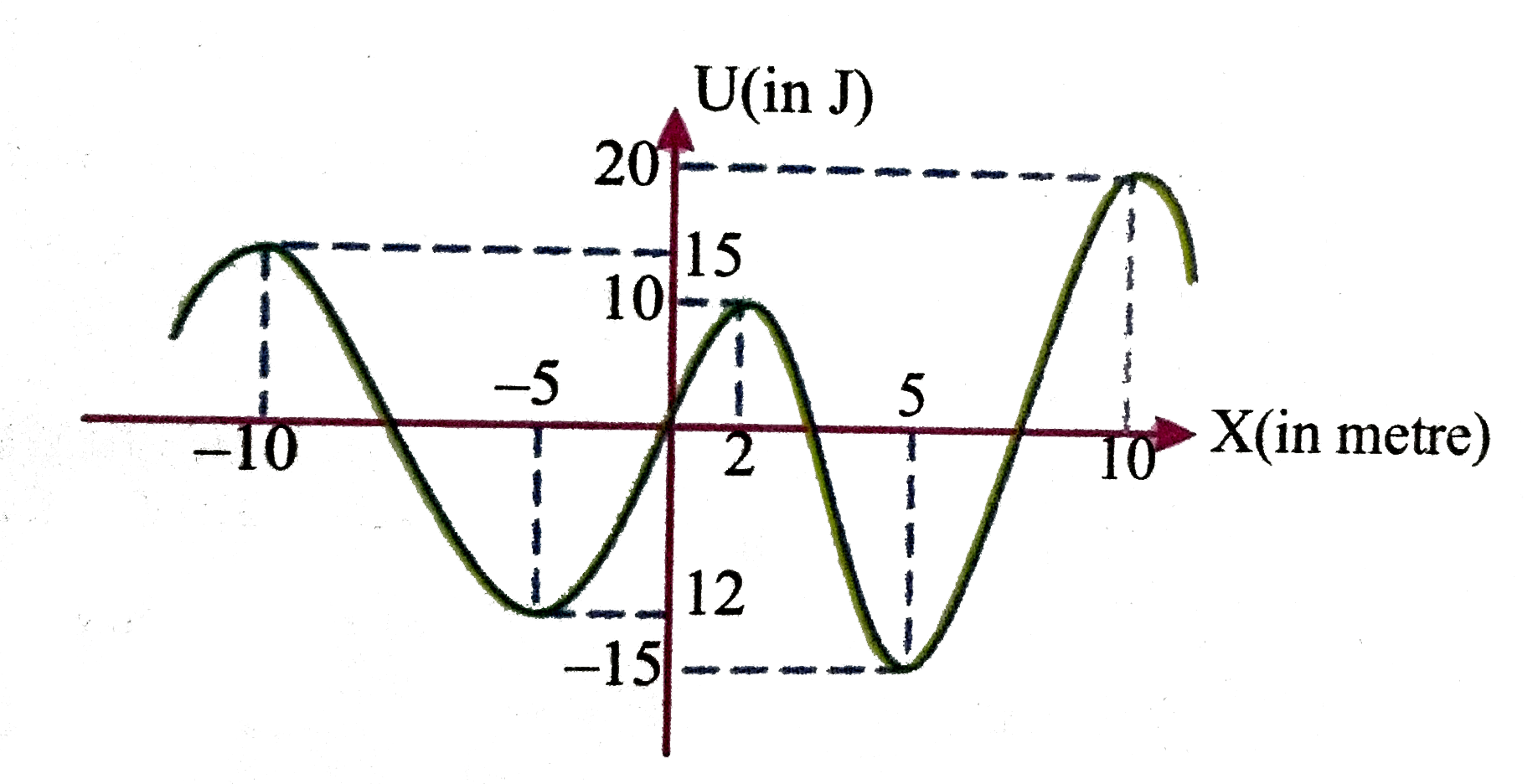
If the particle is released at the origin then
View SolutionIn the figure the variation of potential energy of a particle of mass `m = 2kg` is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
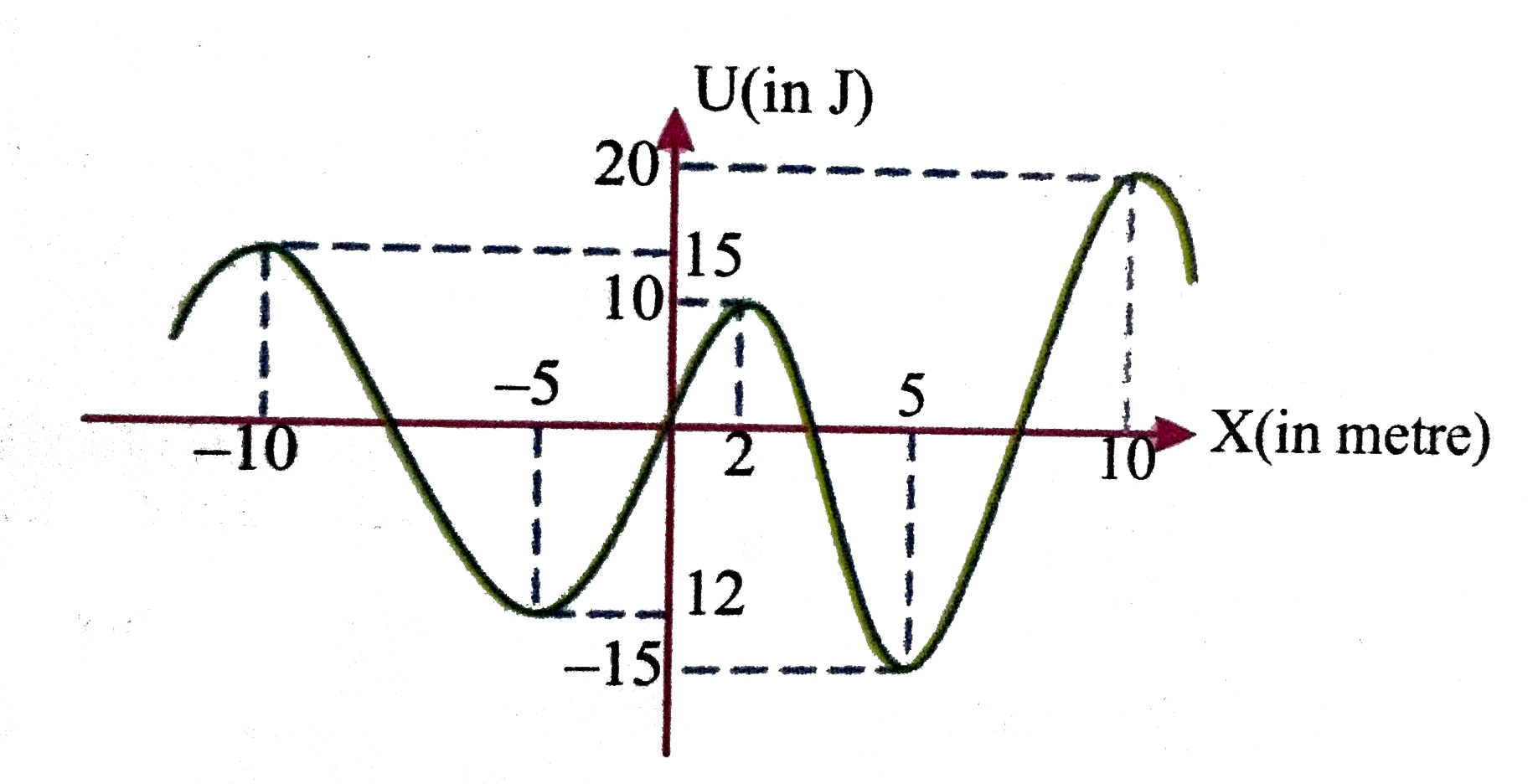
`x = - 5m` and `x = 10 m` position of the particle are respectively of
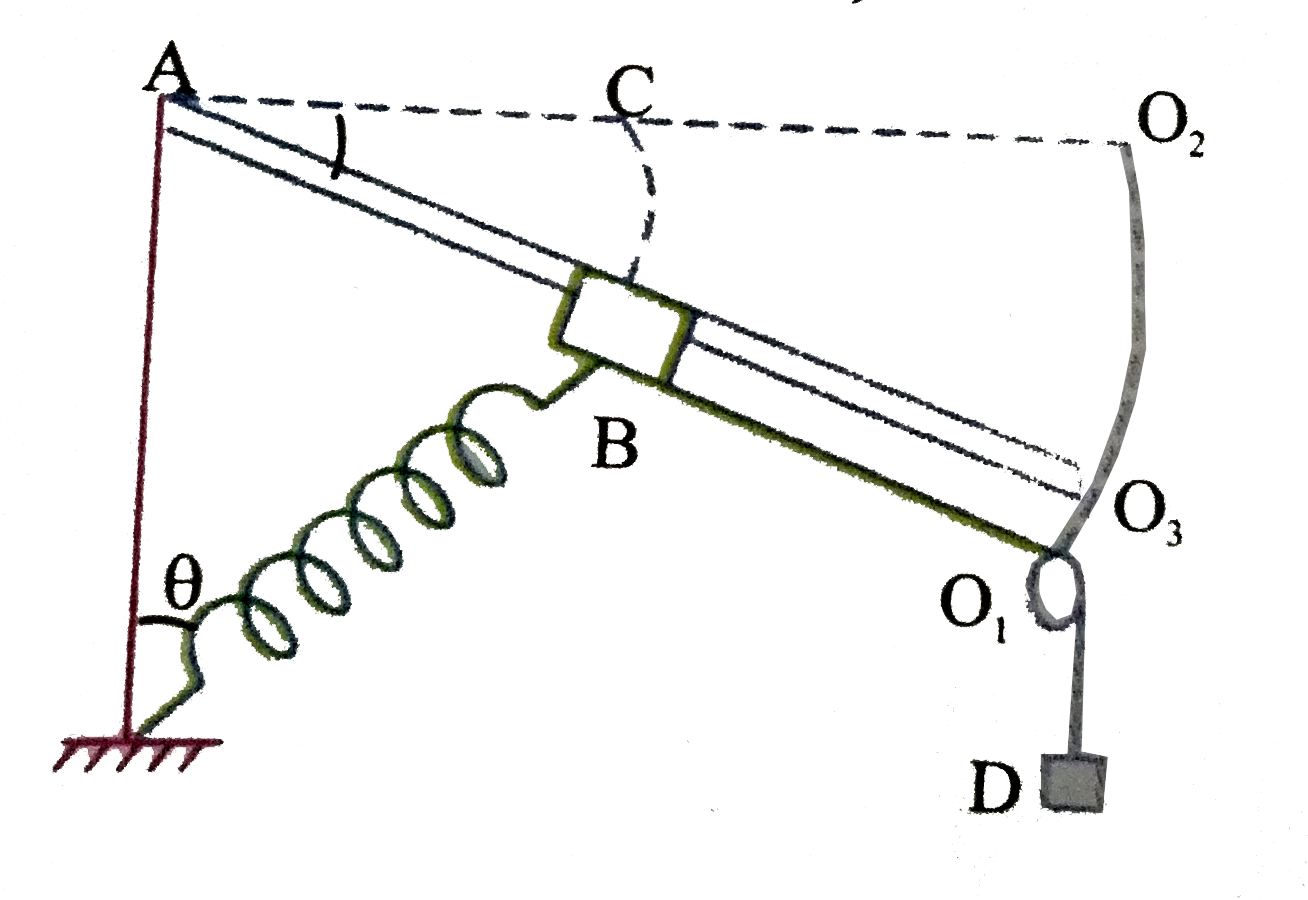
View SolutionRod `AO_(3)` of length `L` can rotate abput `A`. Initially rod was at position `AO_(2)`, when spring `OB` of force constant `K`, attached to block `B` of mass `m` was at position `OA` with unstretched length `L`. The smooth block `B` can slide on rod when pulled by the block `D` of mass `m` through a massless spring and smooth pulley at `O_(1)`.
Find the velocity of the block `B`, when the rod and spring at `B` make an angle of `30^@` with their respective initial positions : (`B` is the middle point of the block)
 .
.
View SolutionRod `AO_(3)` of length `L` can rotate abput `A`. Initially rod was at position `AO_(2)`, when spring `OB` of force constant `K`, attached to block `B` of mass `m` was at position `OA` with unstretched length `L`. The smooth block `B` can slide on rod when pulled by the block `D` of mass `m` through a massless spring and smooth pulley at `O_(1)`.
Find the work done by the frictional force (if slider is rough) at the instant when rod and the spring attached at block `B` make an angle of `30^@` with their respective initial positions.
View SolutionA particle of mass `M` attached to an inextensible strintg is moving in a vertical circle of radius `R`.about fixed point `O`. It is imparted a velocity `u` in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height `h` can be calculated by using formula `v^(2)=u^(2)-2gh`
(ii) Particle will complete the circle if `u ge sqrt(5gR)`
(iii) Particle will oscillates in lower half `(0^(@)ltthetale90^(@))` if `0ltu lesqrt(2gR)`
(iv) The magnitude of tension at a height `'h'` is calculated by using formula `T=M/R[u^(2)+[gR-3gh]]`
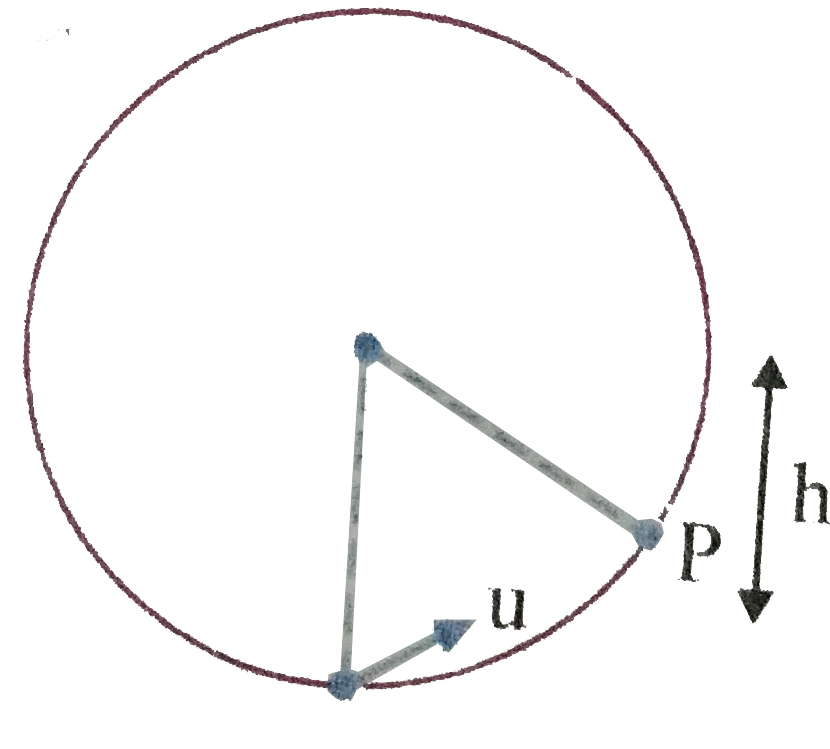
If `R = 2m, M = 2 kg` and `u = 12 m//s`. Then value of tension at lowest position is
View SolutionA particle of mass `M` attached to an inextensible strintg is moving in a vertical circle of radius `R`.about fixed point `O`. It is imparted a velocity `u` in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height `h` can be calculated by using formula `v^(2)=u^(2)-2gh`
(ii) Particle will complete the circle if `u ge sqrt(5gR)`
(iii) Particle will oscillates in lower half `(0^(@)ltthetale90^(@))` if `0ltu lesqrt(2gR)`
(iv) The magnitude of tension at a height `'h'` is calculated by using formula `T=M/R[u^(2)+[gR-3gh]]`
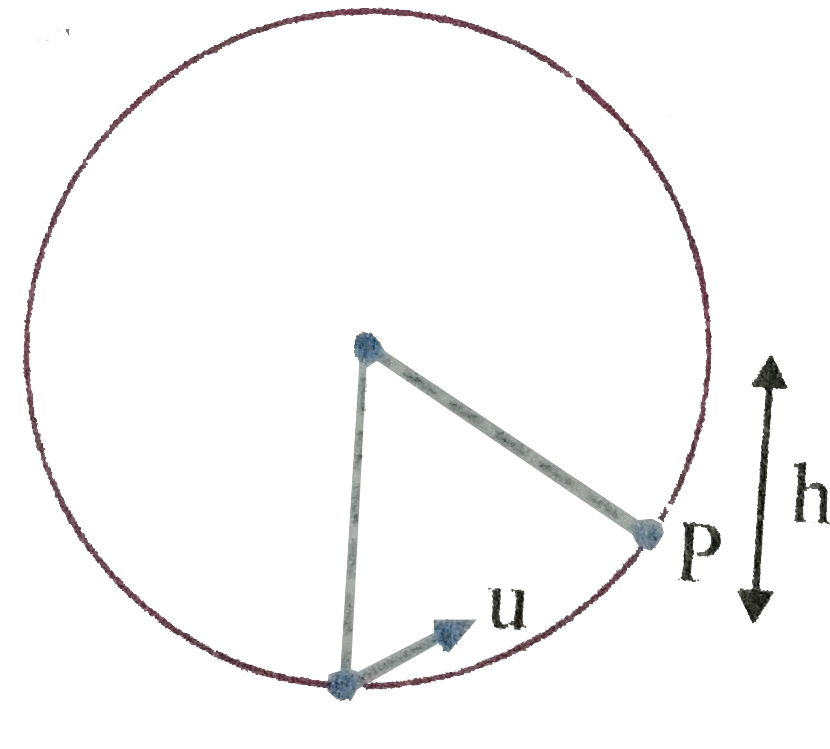
Tension at highest point of its trajectory in above question will be
View SolutionA particle of mass `M` attached to an inextensible strintg is moving in a vertical circle of radius `R`.about fixed point `O`. It is imparted a velocity `u` in horizontal directional at lowest position as shown in figure.
Following information is being given
(i) Velocity at a height `h` can be calculated by using formula `v^(2)=u^(2)-2gh`
(ii) Particle will complete the circle if `u ge sqrt(5gR)`
(iii) Particle will oscillates in lower half `(0^(@)ltthetale90^(@))` if `0ltu lesqrt(2gR)`
(iv) The magnitude of tension at a height `'h'` is calculated by using formula `T=M/R[u^(2)+[gR-3gh]]`
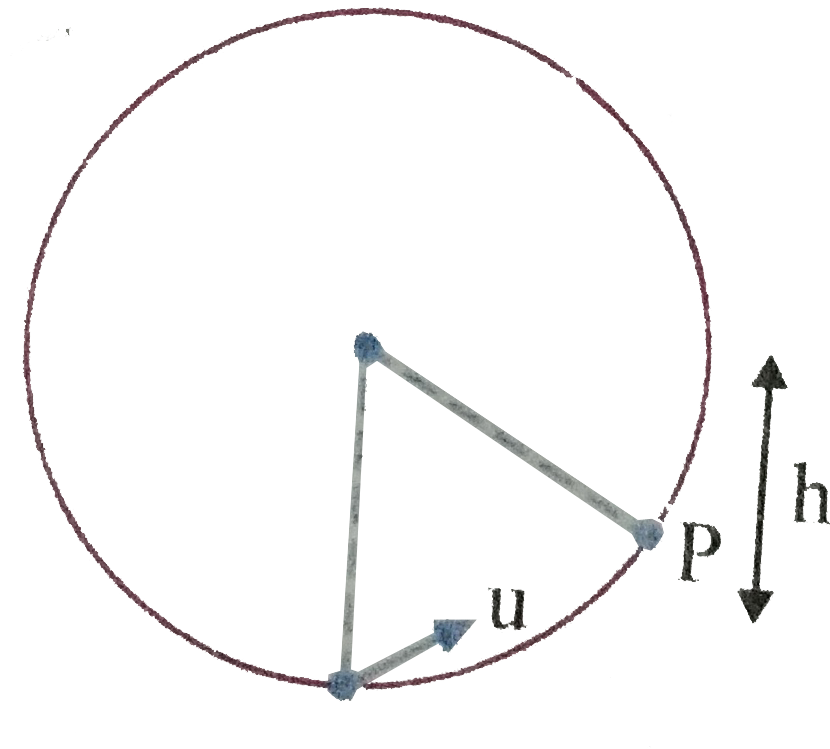
If `M = 2kg, R = 2m` and `u = 10 m//s`. Then velocity of particle when `theta = 60^(@)` is
View SolutionA bead of mass `m` is threaded on a smooth circular wire centre `O`, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant `= (3mg)/(a)` and breaking strength `3mg` connects the bead to the lowest point `A` of the wire. The other end of the string is fixed to ring at point `B` near point `A`. The string is slaked initially. The bead is projected from `A` with speed `u`.
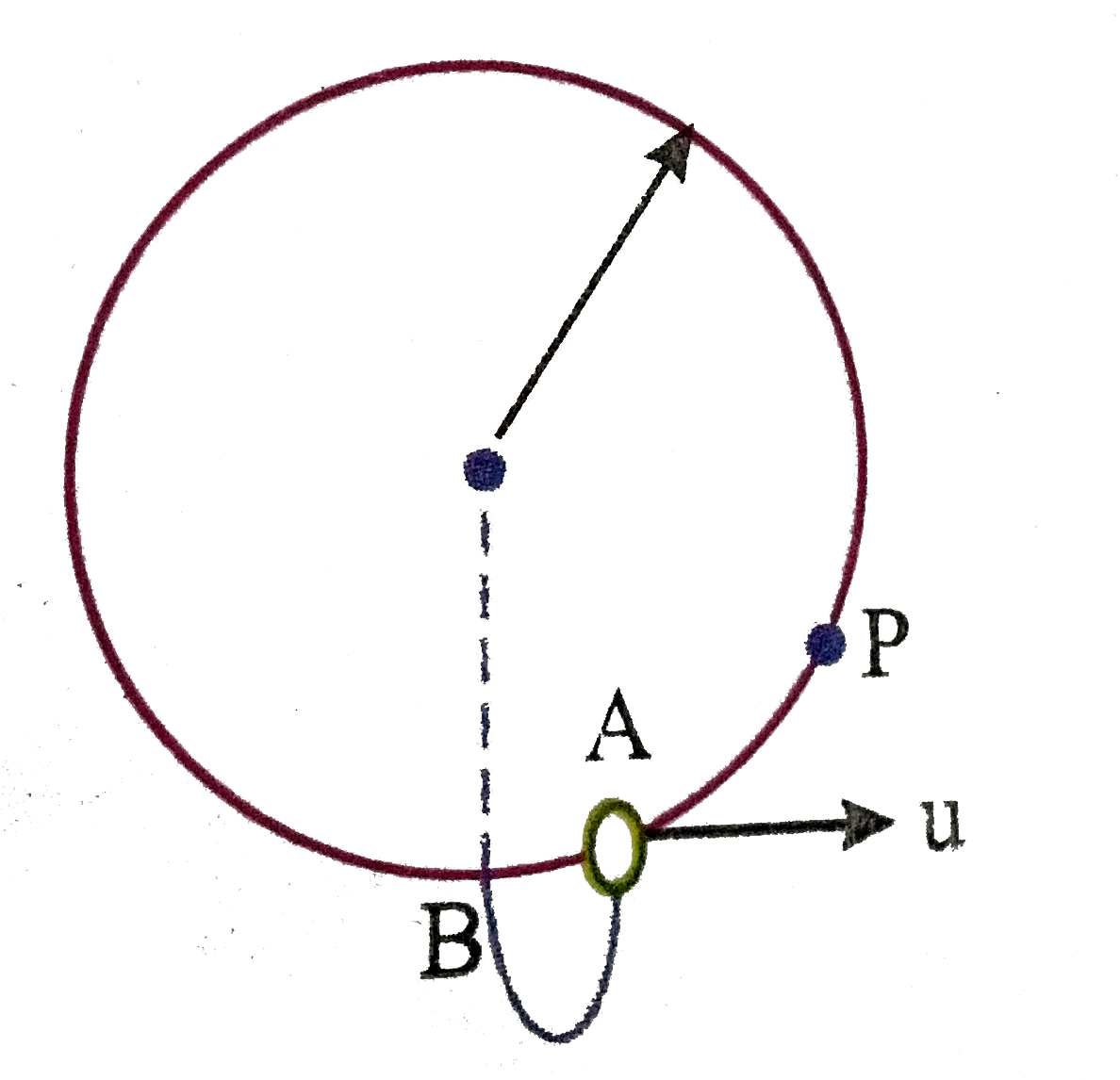
The smallest value `u_(0)` of `u` for which the bead will make complete revolutions of the wire will be
View SolutionA bead of mass `m` is threaded on a smooth circular wire centre `O`, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant `= (3mg)/(a)` and breaking strength `3mg` connects the bead to the lowest point `A` of the wire. The other end of the string is fixed to ring at point `B` near point `A`. The string is slaked initially. The bead is projected from `A` with speed `u`.

If `v =2 u_(0)`, the tension `T` in th elastic string when the bead is at the highest point `B` of the wire is
View SolutionA bead of mass `m` is threaded on a smooth circular wire centre `O`, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant `= (3mg)/(a)` and breaking strength `3mg` connects the bead to the lowest point `A` of the wire. The other end of the string is fixed to ring at point `B` near point `A`. The string is slaked initially. The bead is projected from `A` with speed `u`.
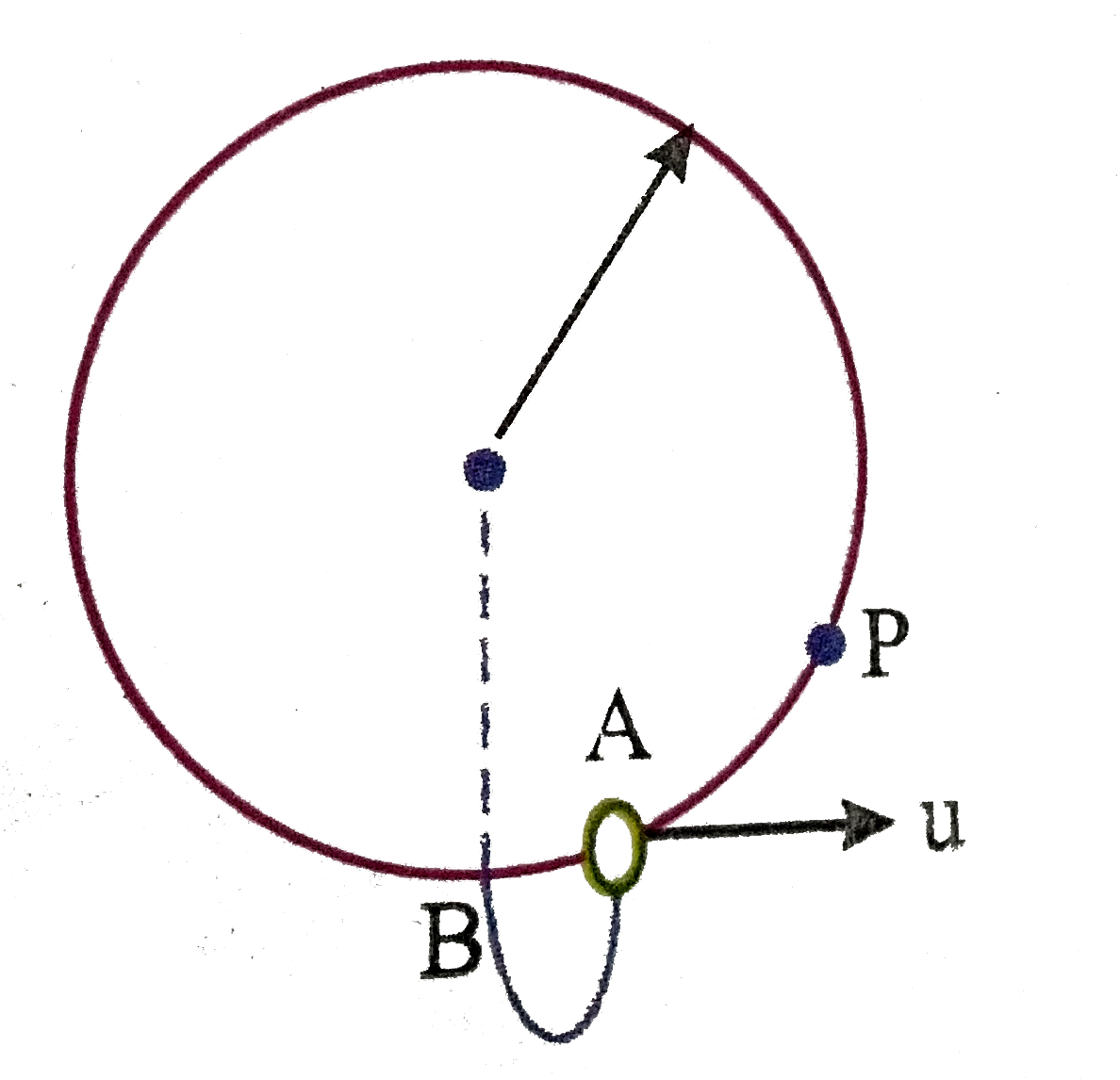
The elastic energy stored in the string when the bead is at the highest point `B` will be
View Solution
Level-VI (Comprehension) questions and complete solutions for chapter WORK POWER AND ENERGY of NARAYANA PHYSICS (HINGLISH) of Class 11