Complete Solutions to Level-V (Single Answer) of chapter WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK POWER AND ENERGY |
| NARAYANA | Level-V (Single Answer) |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A simple pendulum having bob of maas m is suspended from the ceiling of a car used in a stunt film shooting. The car moves up along an inclined cliff at a speed v and makes a jump to leavwe the cliff and lands at some the top of the cliff. The tension in the string when the car is in air is
View SolutionA particle of mass `m` is projected at an angle `alpha` to the horizontal with an initial velocity `u`. The work done by gravity during the time it reaches its highest point is
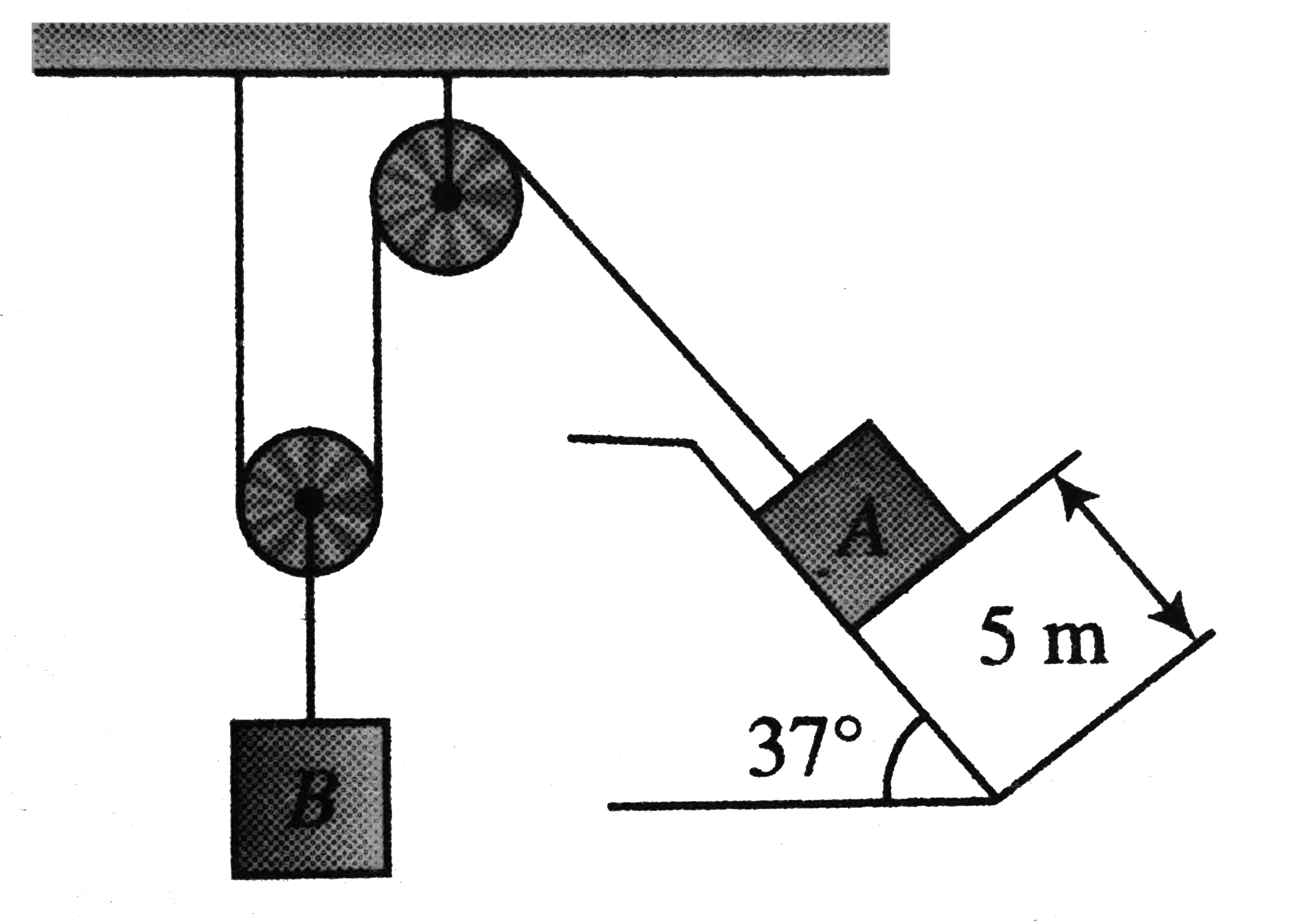
View SolutionThe blocks A and B shown in figure have masses `M_A=5kg` and `M_B=4kg`. The system is released from rest. The speed of B after A has travelled a distance `1m` along the incline is
View SolutionA particle is projected along a horizontal field whose coefficient of friction varies as `mu=A//r^2`, where r is the distance from the origin in meters and A is a positive constant. The initial distance of the particle is `1m` from the origin and its velocity is radially outwards. The minimum initial velocity at this point so the particle never stops is
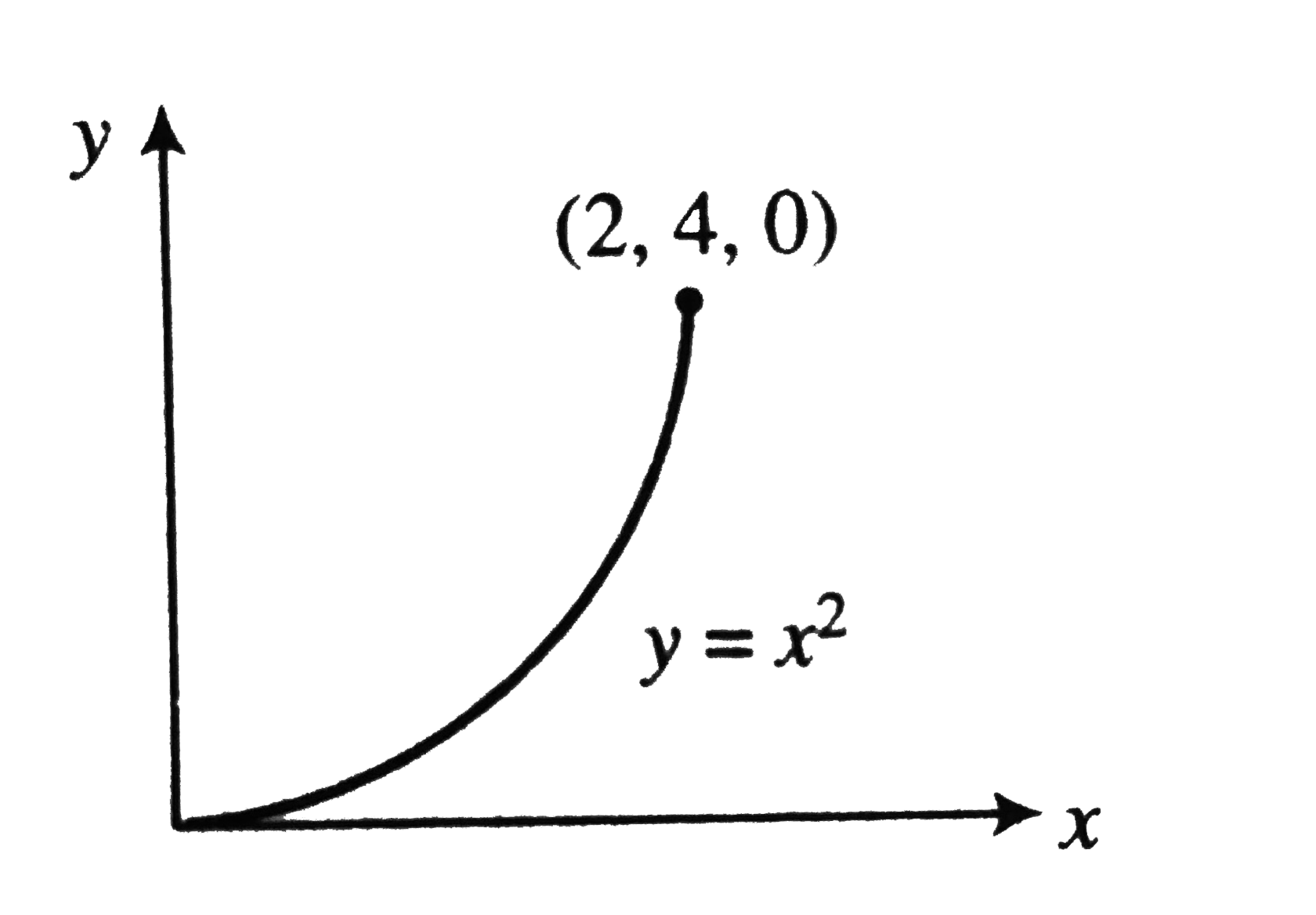
View SolutionA force `vecF=(3xy-5z)hatj+4zhatk` is applied on a particle. The work done by the force when the particle moves from point `(0, 0, 0)` to point `(2, 4, 0)` as shown in figure.
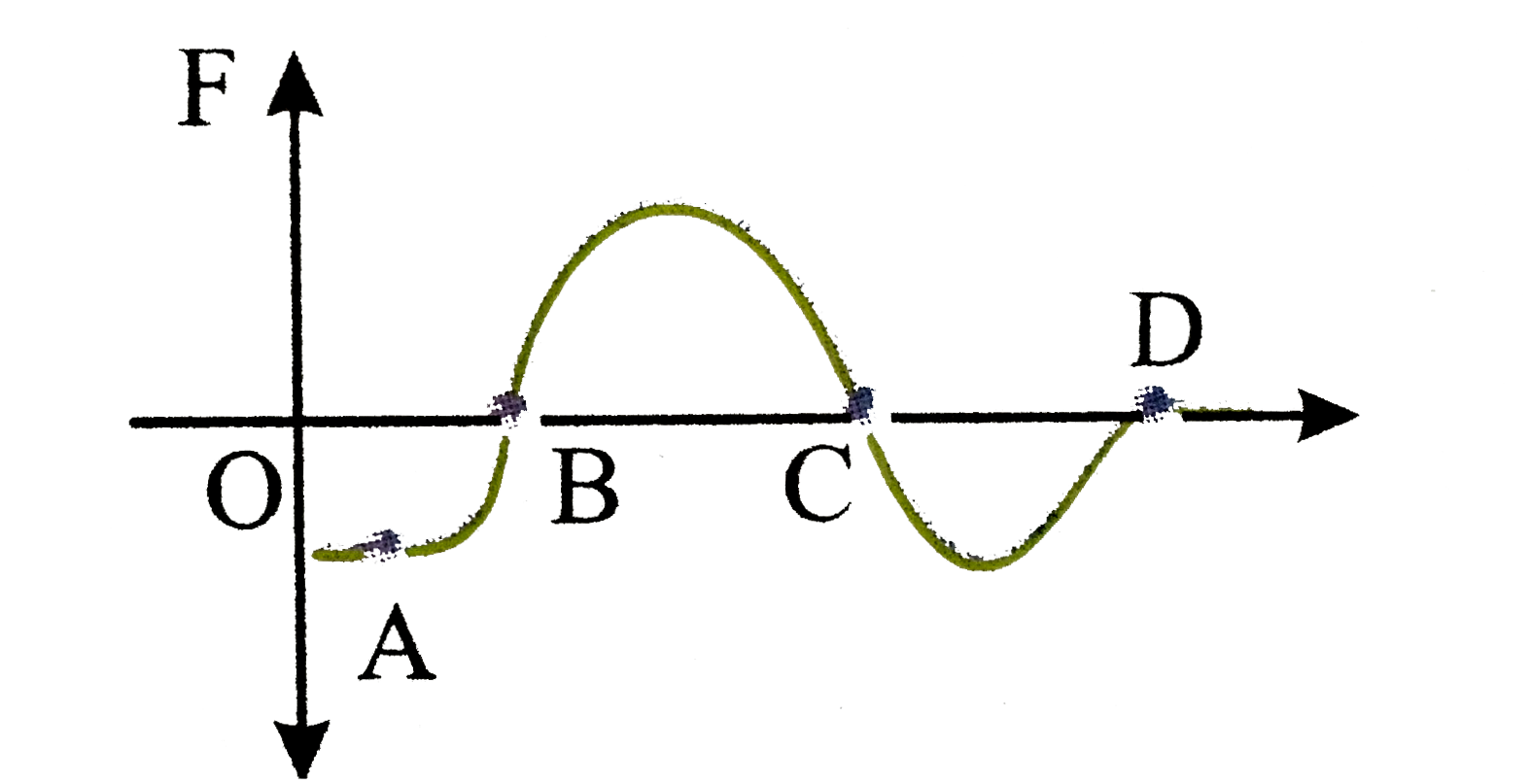
View SolutionA particle is being acted upon by one dimensional conservative force. In the `F-x` curve shown, four points `A,B,C,D` are marked on the curve. State which type of equilibrium is the particle have at position `c`.
 .
.
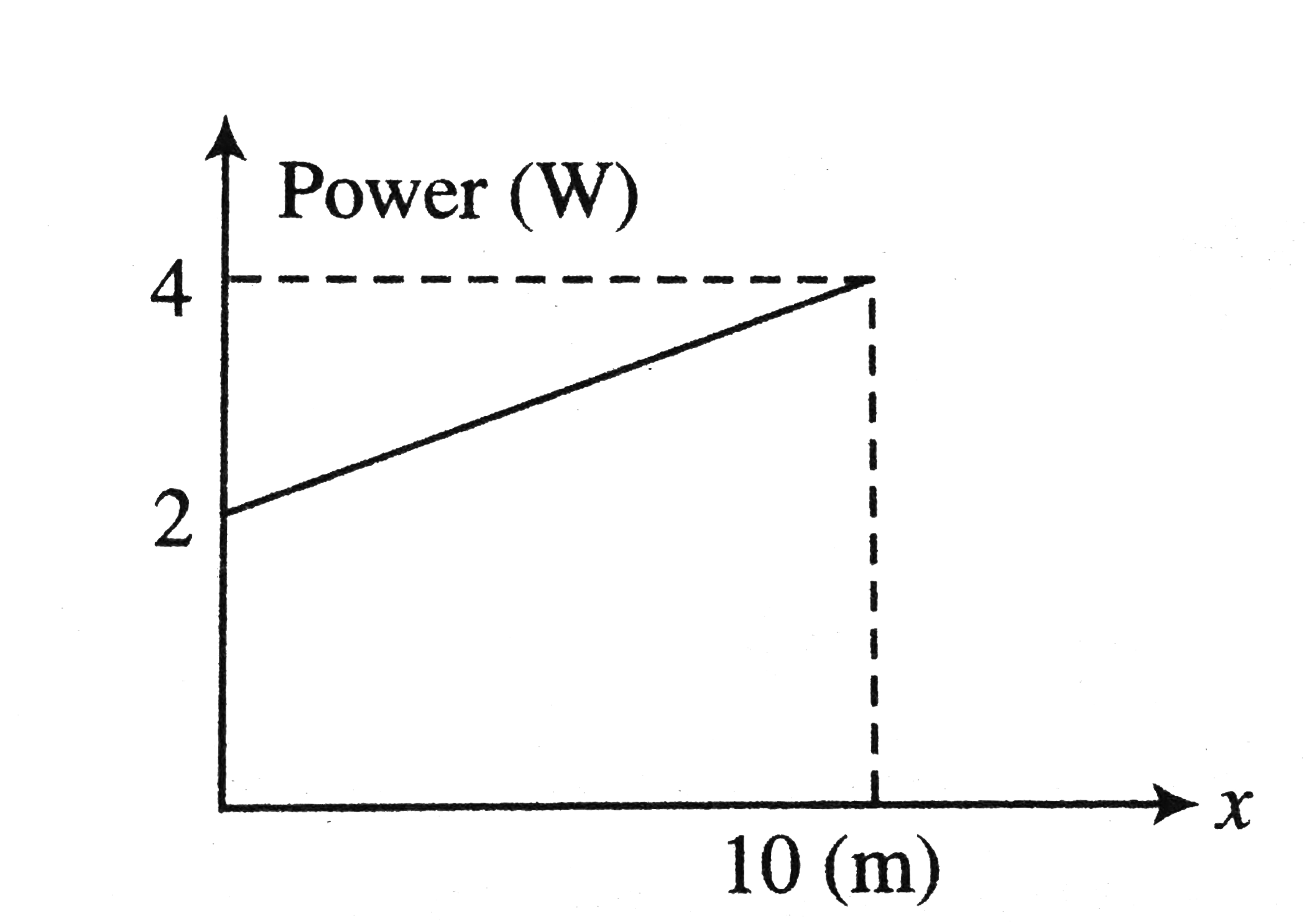
View SolutionA particle A of mass `10//7kg` is moving in the positive direction of `x-axis`. At initial position `x=0`, its velocity is `1ms^-1`, then its velocity at `x=10m` is (use the graph given)
View SolutionThe potential energy of a particle is determined by the expression `U=alpha(x^2+y^2)`, where `alpha` is a positive constant. The particle begins to move from a point with coordinates `(3, 3)`, only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates `(1,1)` is
View SolutionAn engine is hauling a train of mass `m` on a level track at a constant speed `v`. The resistance due to friction is `f`. What power is the engine producing? What extra power must the engine develop to maintain the speed up a gradient 1 in l. What is the new total power developed by the engine develop to maintain the speed up a gradient 1 in l. What is the new total power developed by the engine ?
View SolutionA body of mass m slides down a plane inclined at an angle `alpha`. The coefficient of friction is `mu`. Find the rate at which kinetic plus gravitational potential is dissipated at any time t.
View SolutionIn the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is `vec(u)=(-3 hati+4hatj)`m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
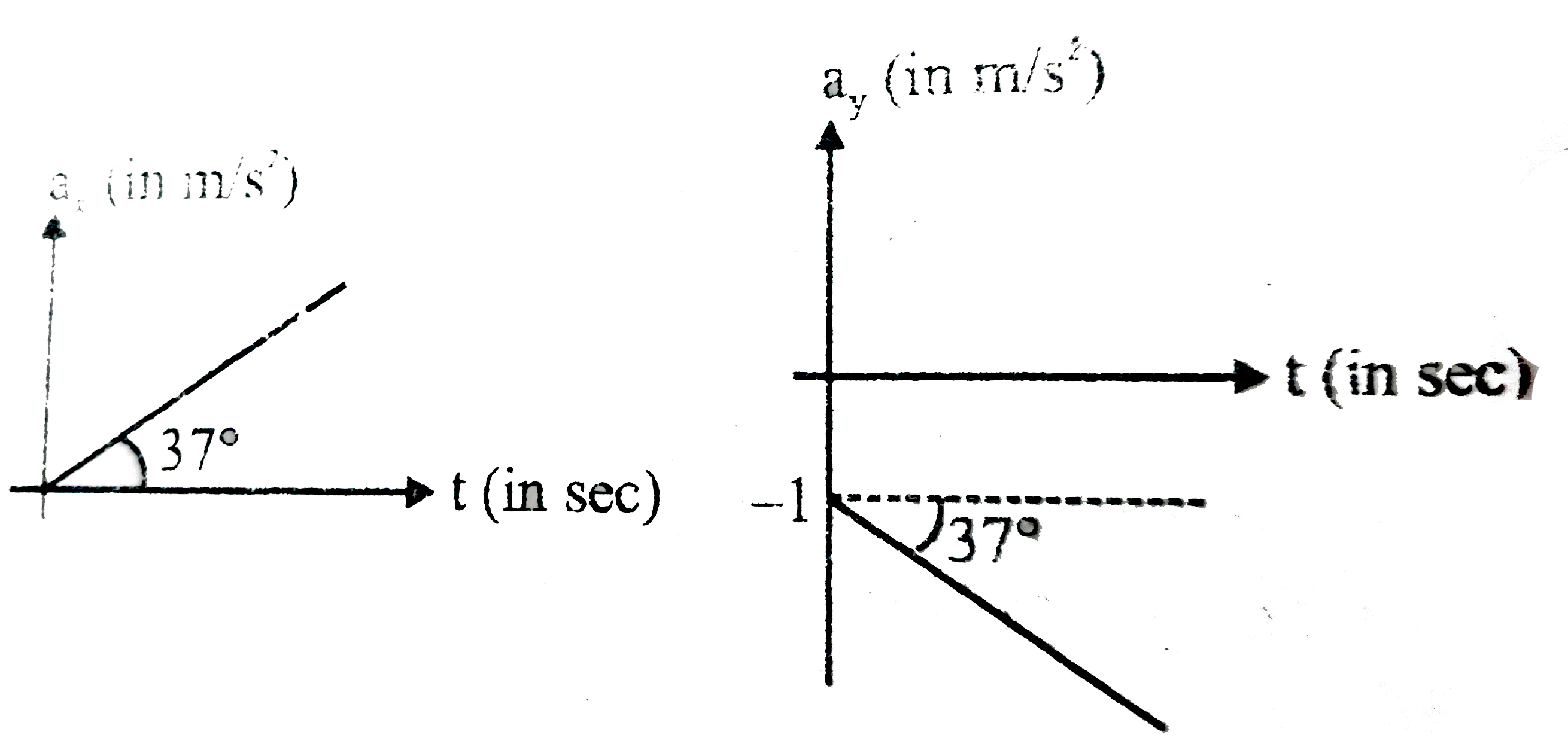
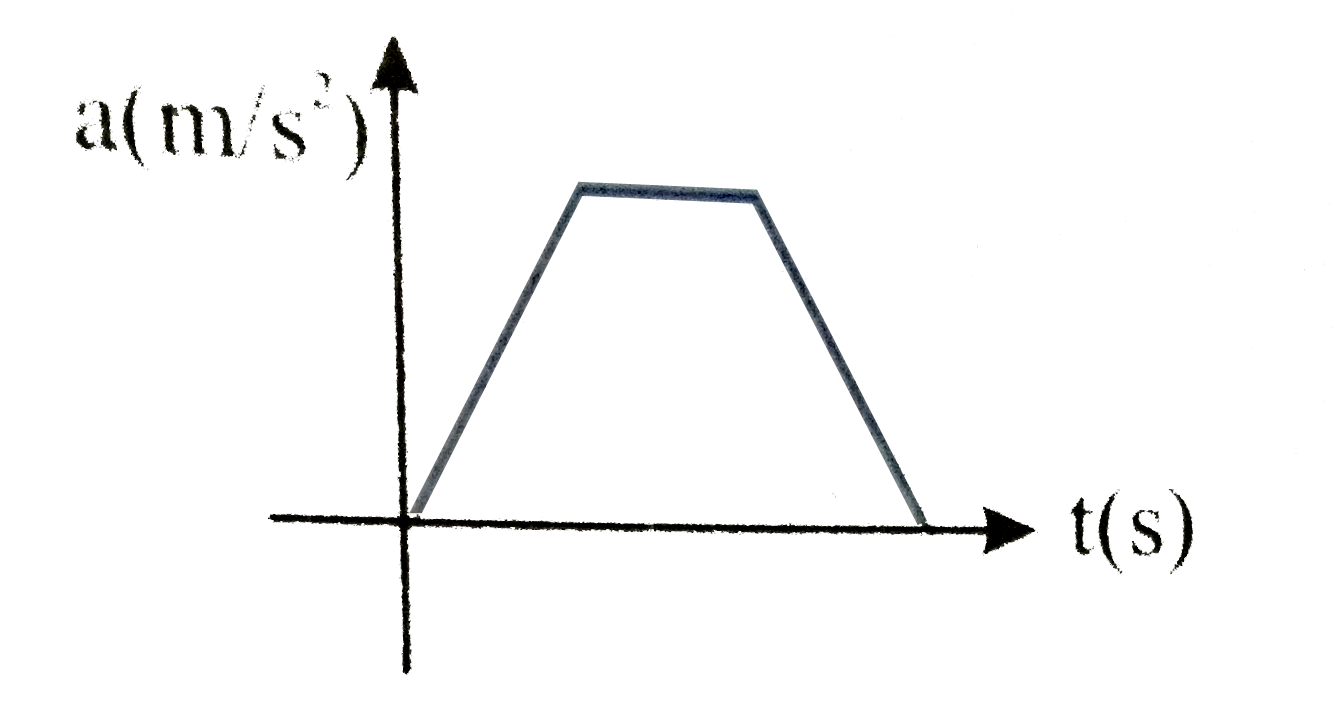
View SolutionFor a particle moving on a straight lint the variation of acceleration with time is given by the graph as shown. Initially the particle was at rest. Then the corresponding kinetic energy of the particle versus time graph will be
 .
.
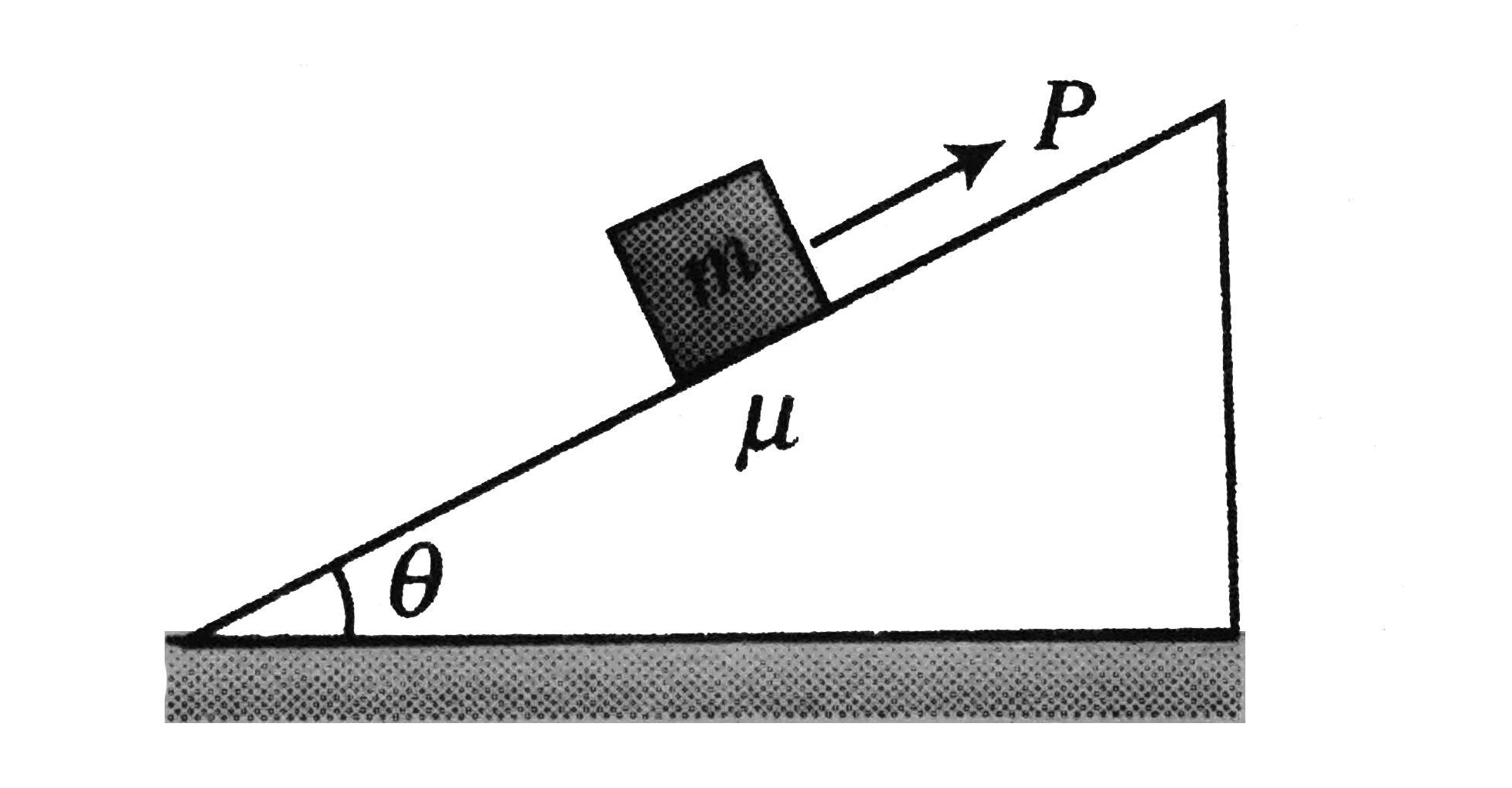
View SolutionA block of mass `m` is being pulled up a rough incline by an agent delivering constant power P. The coefficient of friction between the block and the incline is `mu`. The maximum speed of the block during the course of ascent is
View SolutionThe spring block system lies on a smooth horizontal surface. The free end of the spring is being pulled towards right with constant speed `v_(0) = 2m//s`. At `t = 0 sec`, the spring of constant `k = 100 N//cm` is unstretched and the block has a speed `1 m//s` to left. The maximum extension of the spring is.
 .
.
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant `k`. The masses are pulled a part symmetrically to stretch the spring by a length `x` over its natural length. The work done by the spring on each mass is.
View SolutionA block of mass `m` is allowed to slide down a fixed smooth inclined plane of angle `q` and length `l`. The magnitude of power developed by the gravitational force when the block reaches the bottom is.
View SolutionAn object or mass `(m)` is located at the origin of a vertical plane. The body is projected at an angle `theta` with velocity `u`. The mean power developed by the gravitational force during the interval of time till it reaches maxmum height
View SolutionThe potential enery of a particle varies with posiion `x` according to the relation `U(x) = 2x^(4) - 27 x` the point `x = (3)/(2)` is point of
View SolutionA particle, which is constrained to move along the x-axis, is subjected to a force from the origin as `F(x) = -kx + ax^(3)`. Here `k` and a are origin as `F(x) = -kx + ax^(3)`. Here `k` and a are positive constants. For `x=0`, the functional form of the potential energy `U(x)` of particle is.
View SolutionA force `F = -K(y hatI + x hatj) (where `K` is a posive constant ) acts on a particle moving in the `xy` plane . Starting form the original , the partical is taken along in the positive `x` axis to the point `(x,0)` and then partical to they axis the point `(x,0)` . The total work done by the force `F` on the particls is
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle `theta` it slides.
View SolutionThe potential energy of a `1 kg` particle free to move along the x- axis is given by `V(x) = ((x^(4))/(4) - x^(2)/(2)) J`
The total mechainical energy of the particle is `2 J` . Then , the maximum speed (in m//s) is
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle `theta` it slides.
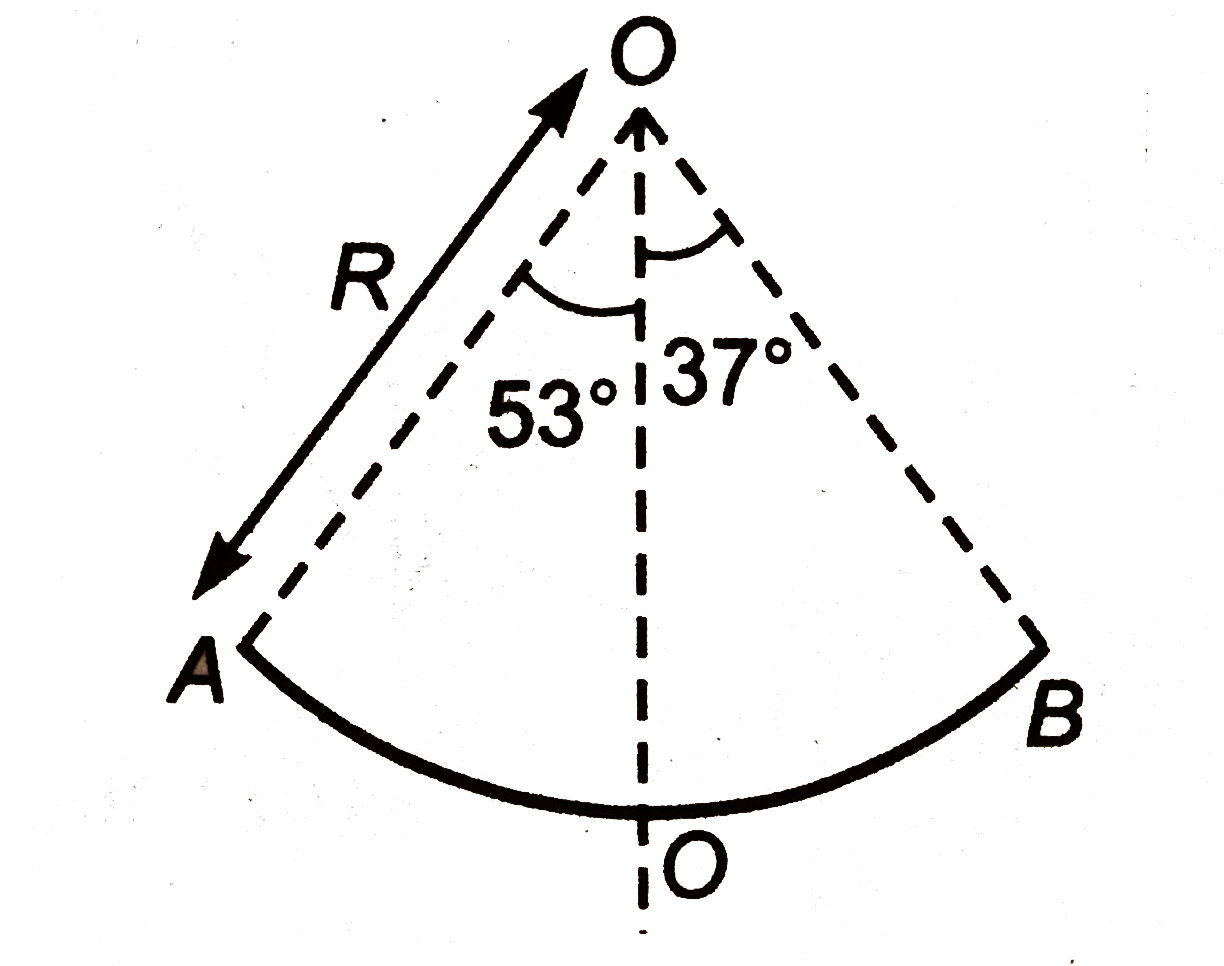
View SolutionA section of fixed smooth circular track of radius `R` in vertical plane is shown in the figure. A block is released from position `A` and leaves the track at `B` The radius of curvature of its trajectory just after it leaves the track `B` is ?
View Solution
Level-V (Single Answer) questions and complete solutions for chapter WORK POWER AND ENERGY of NARAYANA PHYSICS (HINGLISH) of Class 11