Complete Solutions to Level-VI (Single Answer) of chapter WORK POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK POWER AND ENERGY |
| NARAYANA | Level-VI (Single Answer) |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
An engine pumps water continously through a hose. Water leave the hose with a velocity `v` and `m` is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?
View SolutionA hemispherical vessel of radius `R` moving with a constant velocity `v_(0)` and containing a ball, is suddenly haulted. Find the height by which ball will rise in the vessel, provided the surface is smooth :
View SolutionTwo ball of same mass are projected as shown. By compressing equally (say `x`) the springs of different force constants `K_(1)` and `K_(2)` by equal magnitude. The first ball is projected upwards along smooth wall and the other on the rough horizontal floor with coefficient of friction `mu`. If the first ball goes up by height `h`, then the distance covered by the second ball will be :
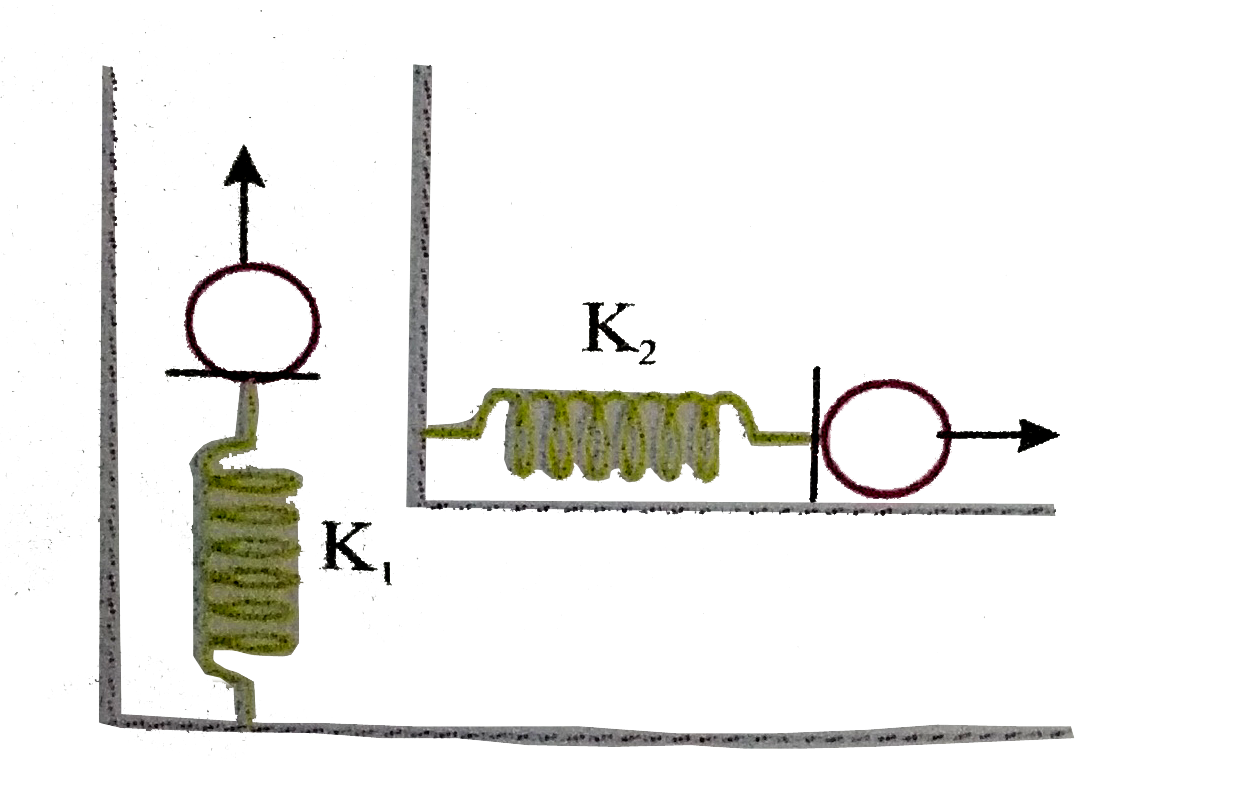 .
.
View SolutionWhat is the minimum value of the mass `M` so that the block is lifted off the table at the instant shown in the diagram ? Assume that the blocks are initially at rest.
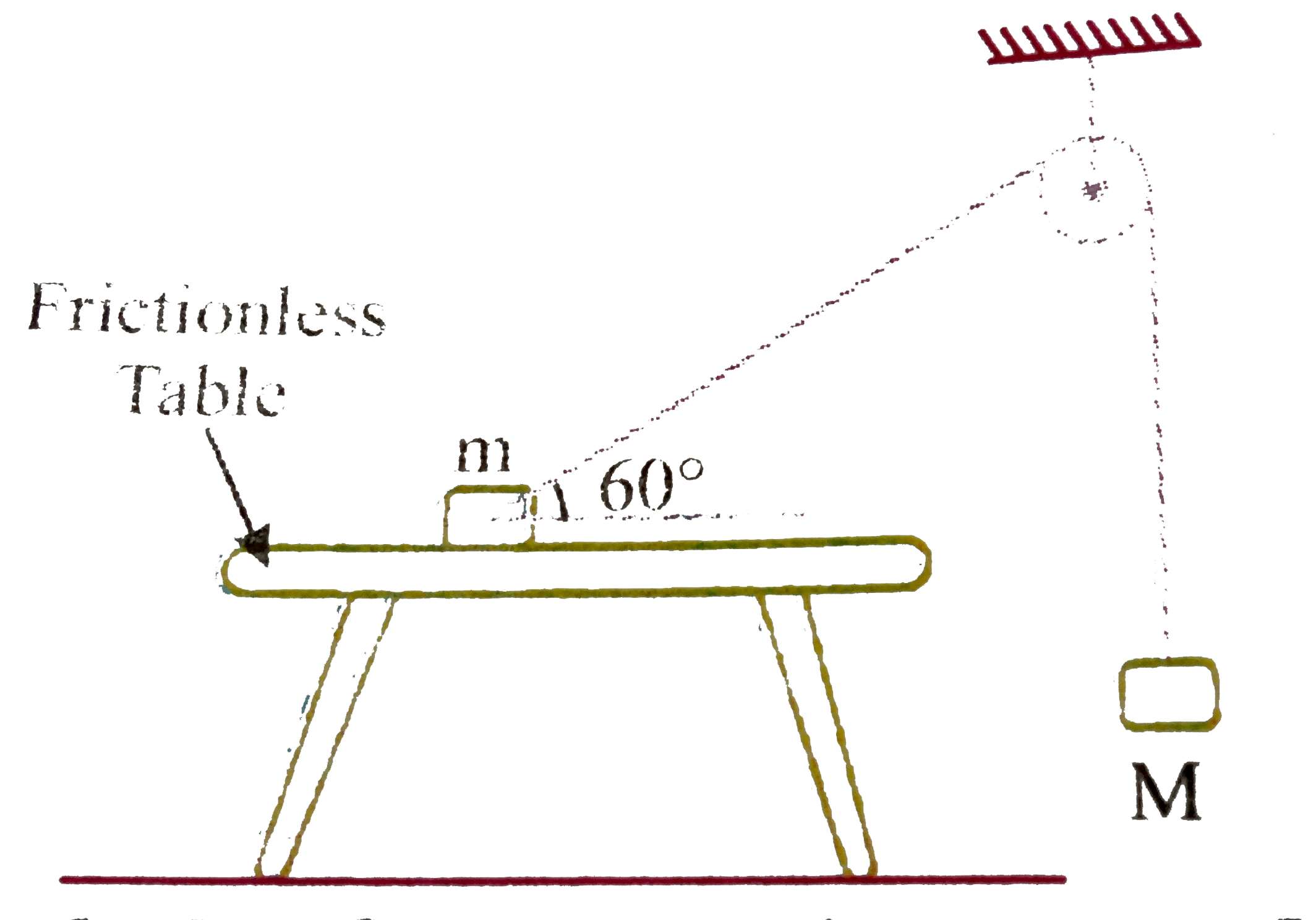 .
.
View SolutionA bob of mass `m` is suspended from a fixed support with a light string and the system with bob and support is moving with a uniform horizontal acceleration. The breaking strength of the string is `mg sqrt(2)`. Find the workdone by the tension in the string in the first one second :
View SolutionA particle moves move on the rough horizontal ground with some initial velocity `V_(0)`. If `(3)/(4)` of its kinetic enegry lost due to friction in time `t_(0)`. The coefficient of friction between the particle and the ground is.
View SolutionThe total mechanical enegry of a particle is `E`. The speed of the particle at `x = ((2E)/(K))^(1//2)` is `((2E)/(m))^(1//2)`. Find the potential energy of the particle at `x` :
View SolutionThe coefficient of friction between a particle moving with some velocity `V_(0)` and the rough horizontal surface is `((V_(0))/(2 g t_(0)))`. Find how much kinetic energy is lost in time `t_(0)` due to friction :
View SolutionA block `A` os mass `m` slides on a smooth slider in the system as shown. A block `c` of mass hanging from a pulley pulls block `A`. When the block `A` was at position `B`, the spring was unstretched. Find the speed of the block `A` when `AB = OB = L`.
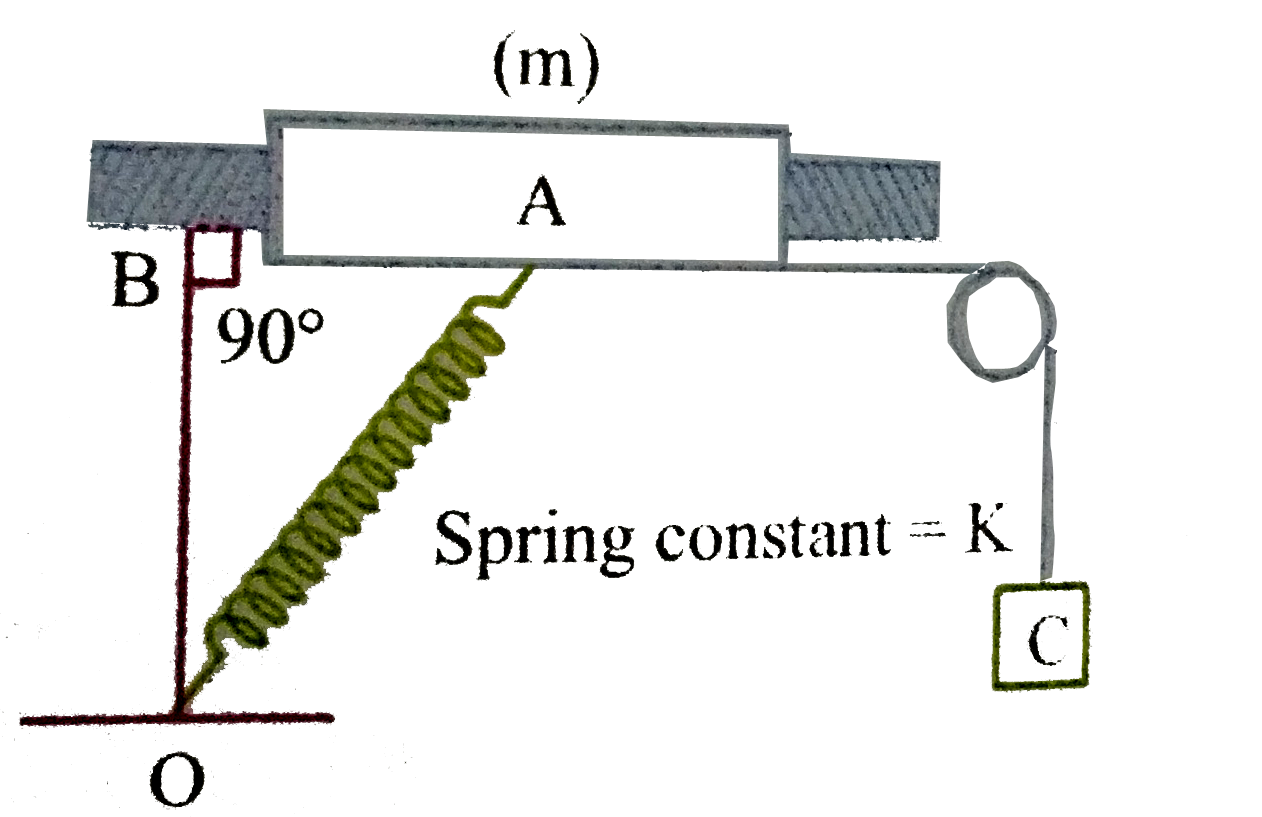 .
.
View SolutionA ring 'A' of mass 'm' is attached to a stretched spring of force constant `K`, which is fixed at `C` on a smooth vertical circular track of radius `R`. Points `A` and `C` are diametrically opposite. When the ring slips form rest in the track to point `B`, making an angle of `30^@` with `AC`. `(/_ ACB = 30^@)` spring becomes unstretched. Find the velocity of the ring at `B`.
 .
.
View Solution`A` and `B` are smooth light hinges equidistant from `C`, which can slides on `ABC`. The spring of force constant `K` is fixed at its one end `C` and conncented to light rods `AD` and `BD` at point `D`. A block of mass `m` is suspended at `D`. Find the velocity of the block, when `/_ CAD` changes from `30^@` to `45^@. AD = BD = L`.
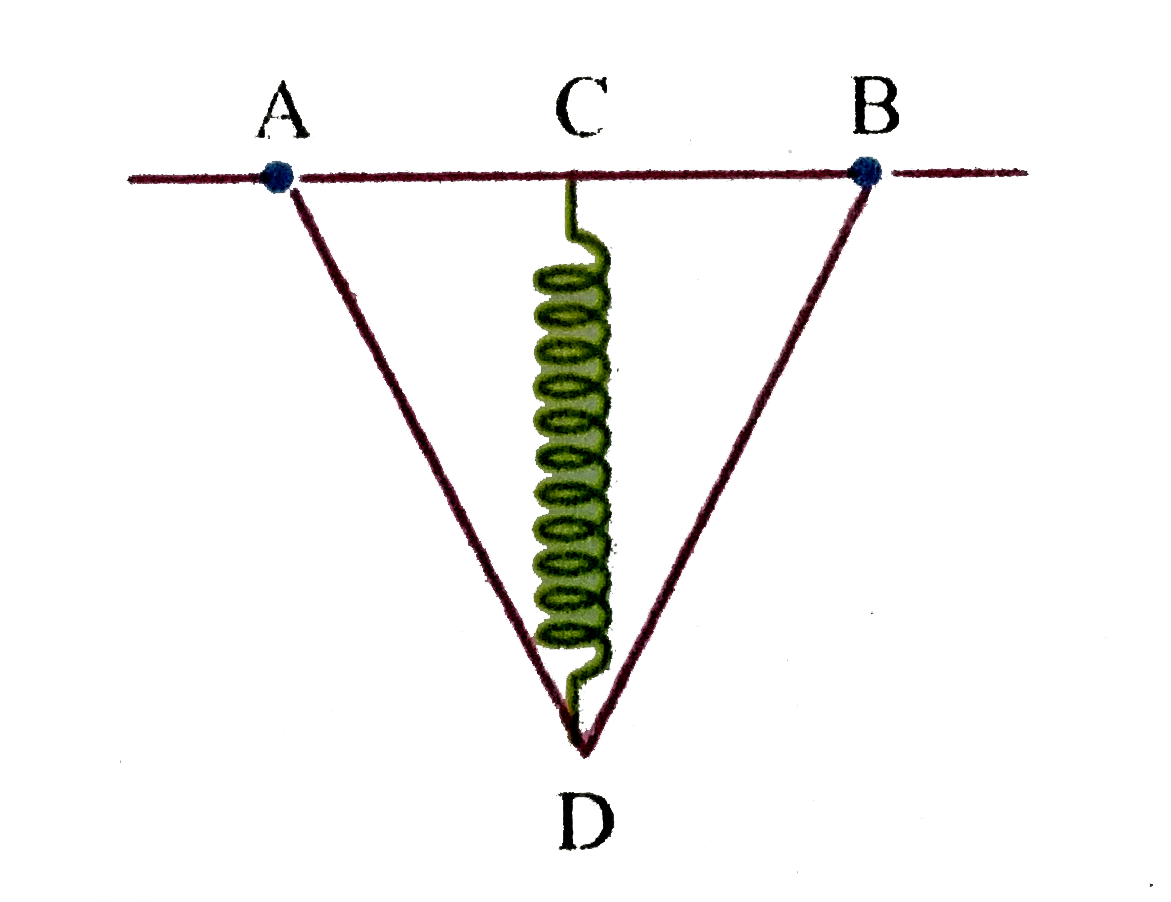 .
.
View SolutionThree springs `A,B` and `C` each of force constant `K`, are connected at `O`. The other ends of `B` and `C` can slide on smooth sliders. A pan is hanging from other end of the spring `A`. When a block of mass `m` is placed into he pan, find the amount of workdone by the gravity on block system after it stops vibrating. The spring `C` does not sag :
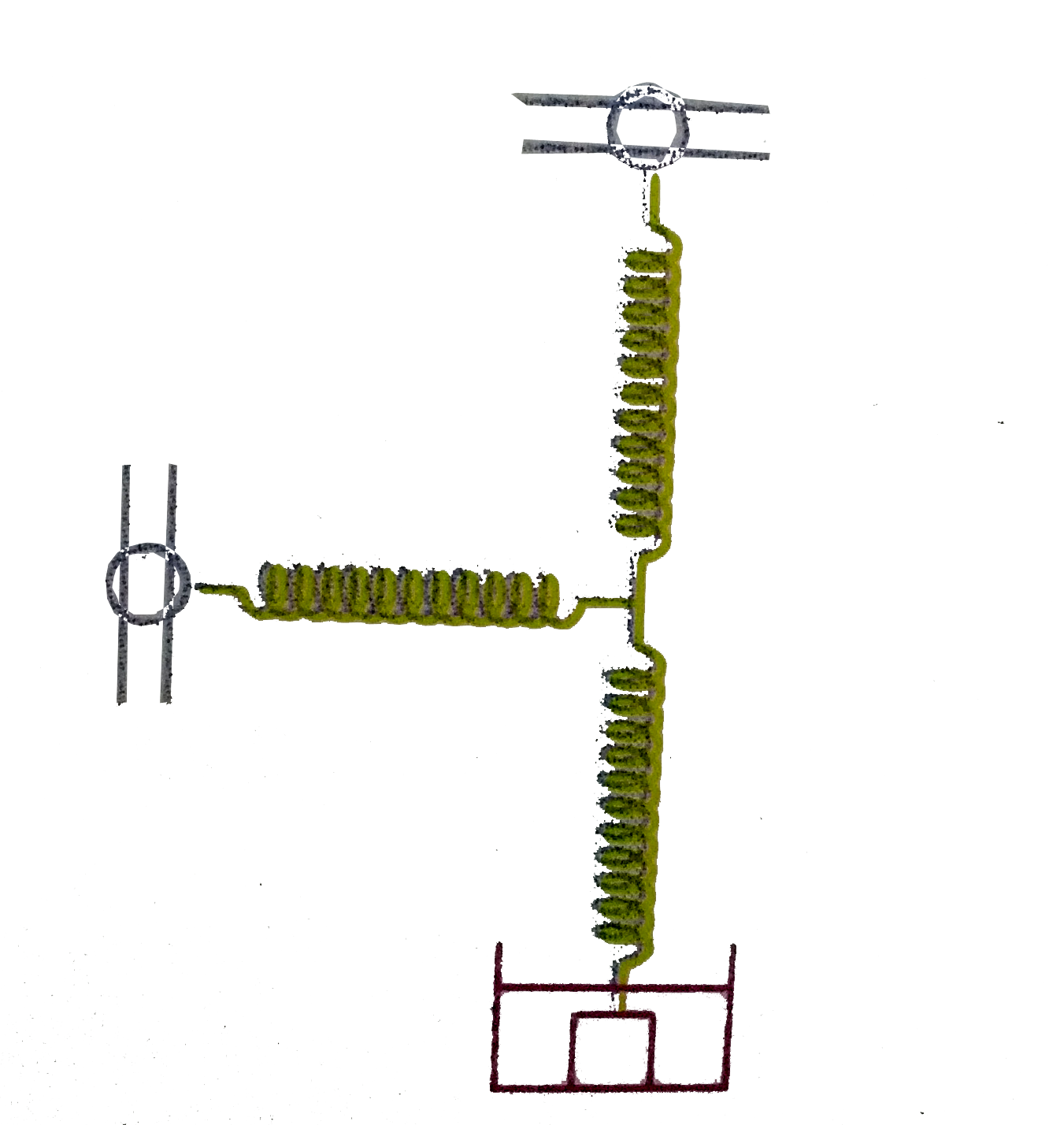 .
.
View SolutionA rope of length `l` and mass 'm' is connected to a chain of length `l` and mass `2 m` and hung vertically as shown. What is the change in graviational potential energy if the system is inverted and hung from same point.
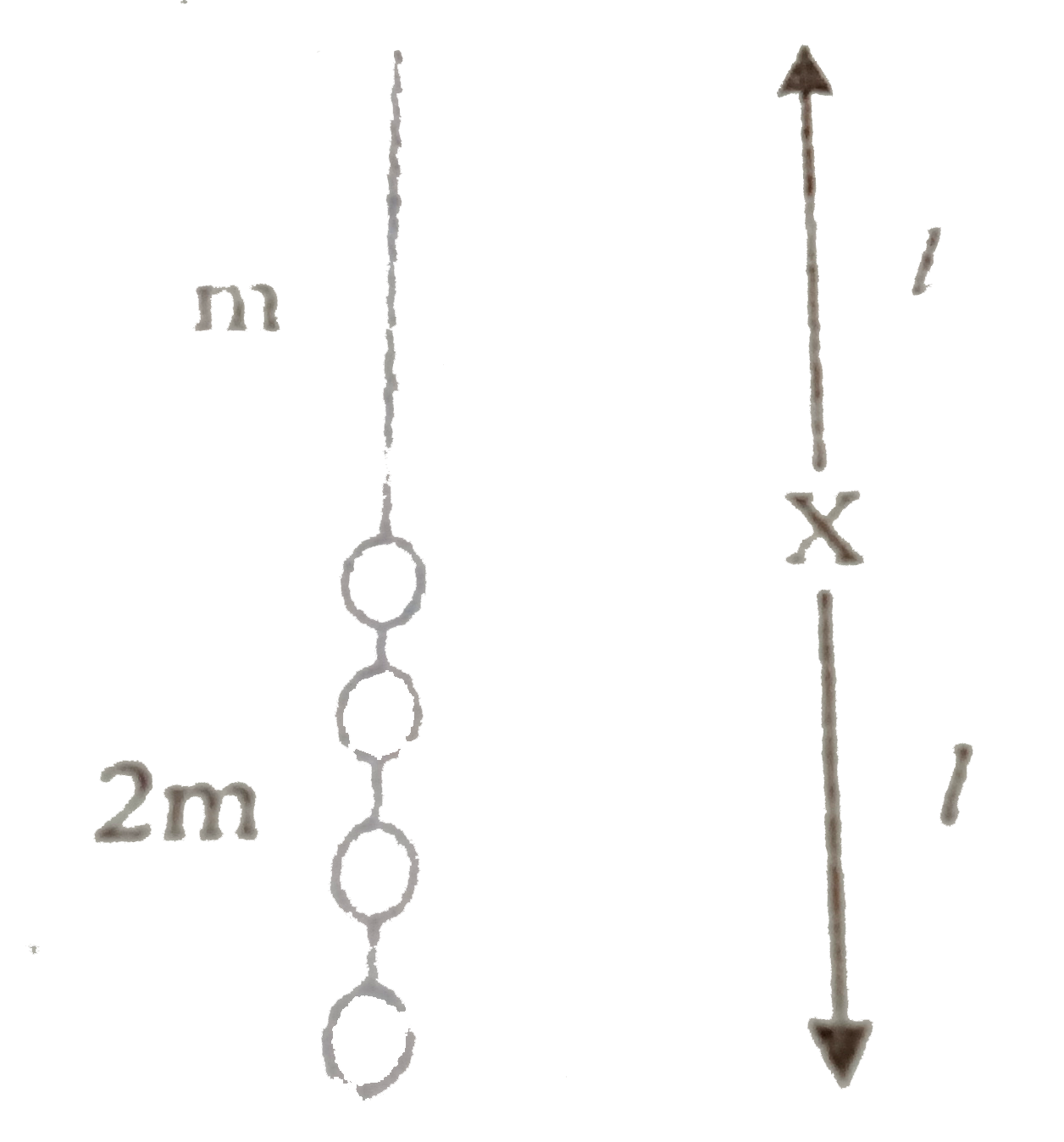 .
.
View SolutionIn the figure shown all the surfaces are frictionless and mass of block `m=1kg`, block and wedge are held initially at rest, now wedge is given a horizontal acceleration of `10 m//s^(2)` by applying a force on the wedge so that the block does not slip on the wedge, the work done by normal force in ground frame on the block in `sqrt(3) sec` is
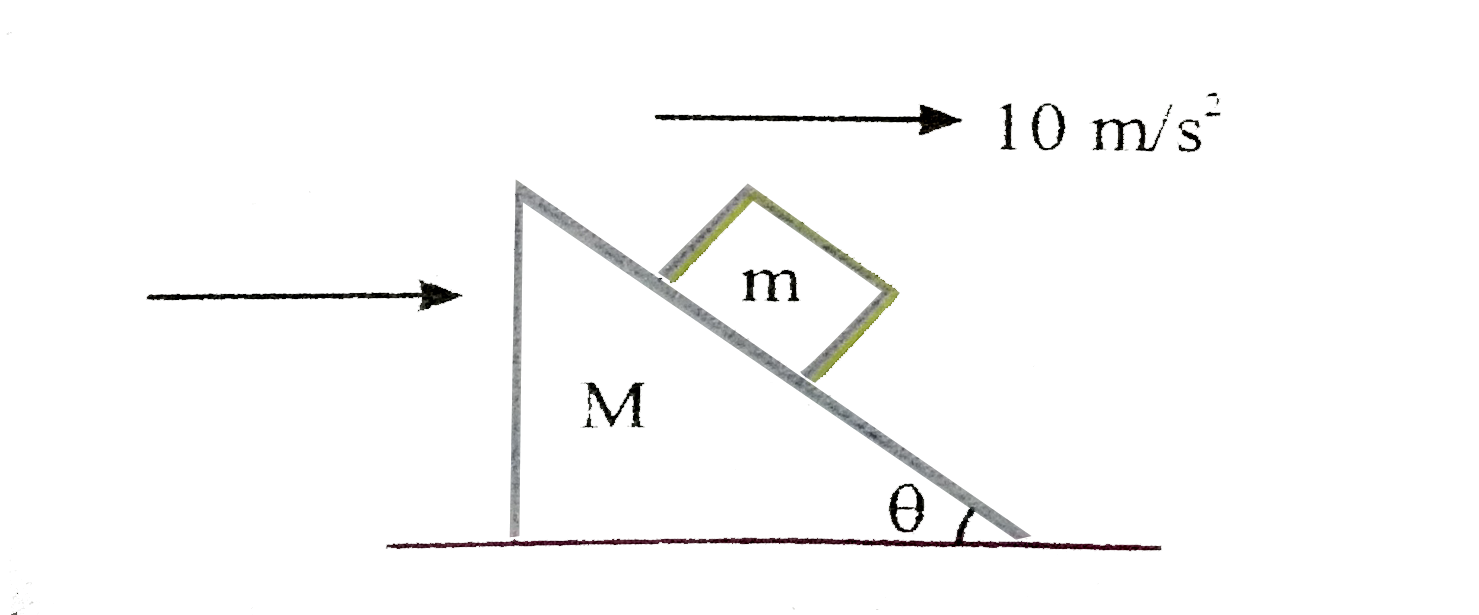 .
.
View SolutionA ring of mass `m` can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant `k = 4 mg//R`, where `2R` is the natural length of the spring . The other end of spring is fixed to the ground at a horizontal distance `2R` from base of the rod . If the mass is released at a height `1.5 J` then the velocity of the ring as it reaches the ground is

View SolutionA small body A starts sliding from the height h down an inclined groove passing into a half-circle of radius `h//2` (figure).

Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).
View Solution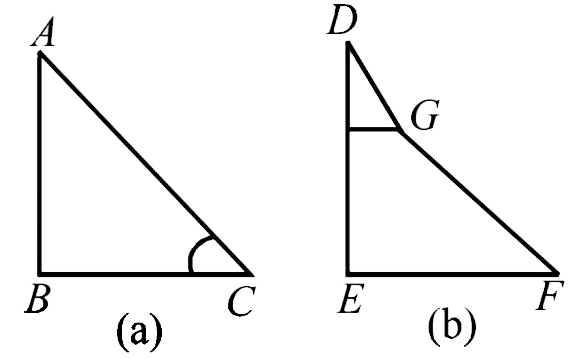
In the figure (a) and (b) `AC` and `GF` are fixed inclined planes `BC = EF = x` and `AB = DE = y` A small block of mass `M` is rdeased from the point `A` it sides down `AC` and maches `C` with a speed `V_(C) ` The same block is relessed from rest from the point `D` it sides down `DGF` and reached the point the `F` with `V_(p) THe coefficients of kiletic friction between the block and the sarface `AC` and `DGF` are `mu` colculate `V_(C) ` and V_`(p)`
View SolutionA `0.5kg` block slides from the point A on a horizontal track with an initial speed `3 m//s` towards a weightless horizontal spring of length `1m` and force constant `2N//m.` The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and `0.20` respectively. If the distances AB and BD are `2m` and `2.14m` respectively, find total distance through which the block moves before it comes to rest completely. `(g=10 m//s^(2) ).
View SolutionA block of mass `1 kg` kept over a smooth surface is given velocity `2 m//s` towards a spring of spring constant `1 N//m` at a distance of `10 m`. Find after what time block will be passing through `P` again
 .
.
View SolutionA body is displaced from `(0,0)` to `(1 m, 1m)` along the path `x = y` by a force `F=(x^(2) hatj + y hati)N`. The work done by this force will be
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as `F = (alpha)/(upsilon)` where `alpha` is constant. The work done by this force in time interval `Delta t` is :
View SolutionA particle of mass `m` initially at rest starts moving from point `A` on the surface of a fixed smooth hemisphere of radius `r` as shown. The particle looses its contact with hemisphere at point `B.C` is centre of the hemisphere. The equation relating `theta` and `theta'` is
 .
.
View SolutionA bob attached to one end of a string, other end of which is fixed at peg `A`. The bob is taken to a position where string makes an angle of to a position where string makes an angle of `30^@` with the horizontal. On the circular path of the bob in vertical plane there is a ped 'B' at a symmetrical position with respect to the position of release as shown in the figure. If `V_(c)` and `V_(a)` be the minimum speeds is clockwise and anticlock wise directions respectively, given to the bob in order to hit the ped 'B' then ratio `V_(c) : V_(a)` is equal to
 .
.
View SolutionA wind - powered generator convets and energy into electrical energy . Assume that the generator convents a fixed fraction of the wind energy intercepited by to blades into electrical energy for wind speed `V` , the electrical power output will be propertional to
View SolutionAn ideal spring with spring - constant `K` is bung from the colling and `a` block of mass `M` is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
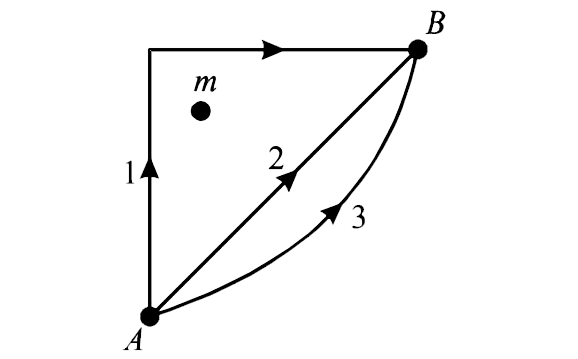
View SolutionIf `W_(1) W_(2)` and `W_(3)` represent the work done in moving a particle from `A` to `B` along three different paths `1.2` and`3` respectively (asshown ) in the gravitational fieled of a point mass m, find the correct relation between ` `W_(1) W_(2)` and `W_(3)`
View SolutionA particle is acted by `x` force `F = Kx` where `K` is `a( + Ve)` constant its potential mwrgy at `x = 0` is zero . Which curve correctly represent the variation of putential energy of the block with repect to `x`
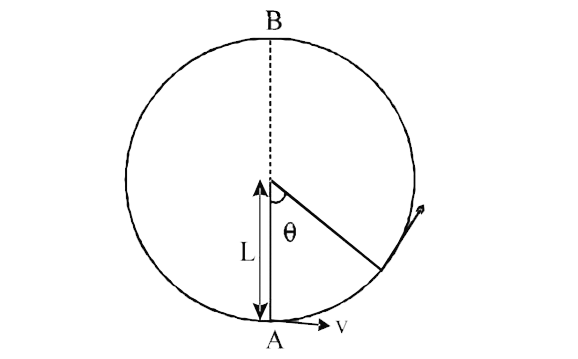
View SolutionA bob of mass M is suspended by a massless string of length L. The horizonta velocity v at position A is just sufficient to make it reach the point B. The angle `theta` at which the speed of the bob is half of that at A, satisfies
View SolutionThe work done an a particle of mass `m` by a force
`K[(x)/((x^(2) + y^(2))^(3//2)) hati +(y)/((x^(2) + y^(2^(3//2))) hatj)]
(K being a constant of appropriate dimensions), when the partical is taken from the point `(a,0)` to the point `(0,a)` along a circular path of radius a about the origin in x - y plane is
View SolutionA tennis ball dropped on a barizoontal smooth surface , it because back to its original postion after hiting the surface the force on the bell during the collision is propertional to the length of compression of the bell . Which one of the following skethes desches discribe the variation of its kinetic energy `K` with time `1` mass apporiandly ? The figure as only illistrative and not to the scale .
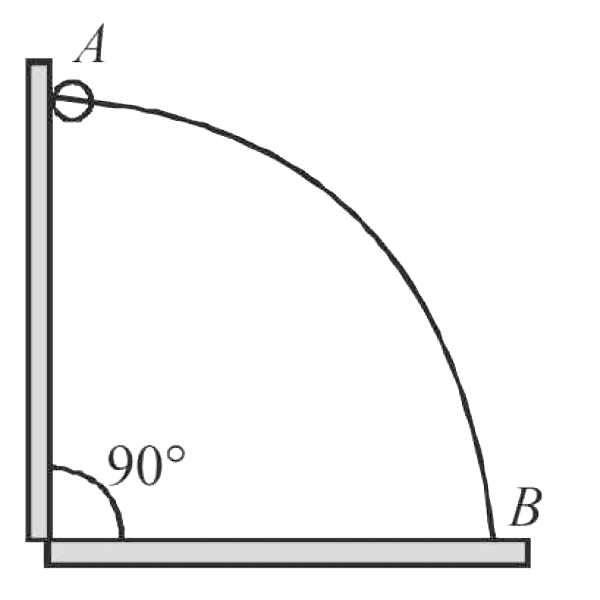
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View Solution
Level-VI (Single Answer) questions and complete solutions for chapter WORK POWER AND ENERGY of NARAYANA PHYSICS (HINGLISH) of Class 11