Complete Solutions to LEVEL I(C.W.) of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | LEVEL I(C.W.) |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
If `'A'` is areal velocity of a planet of mass `M`, its angular momentum is
View SolutionA planet revolves round the sun in an elliptical orbit of semi minor and semi major axes `x` and `y` respectively. Then the time period of revolution is proportional to
View SolutionLet `'A'` be the area swept by the line joining the earth and the sun during Feb `2012`. The area swept by the same line during the first week of that month is
View SolutionA satellite moving in a circular path of radius `r` around earth has a time period `T`. If its radius slightly increases by `4%`, then percentage change in its time period is
View SolutionThe time of revolution of planet `A` round the sun is `8` times that of another planet `B`. The distance of planet `A` from the sun is how many `B` from the sun
View SolutionThe distance of Neptune and Saturn from the Sun are respectively `10^(13)` and `10^(12)` meters and their periodic times are respectively `T_n` and `T_s`. If their orbits are circular, then the value of `T_n//T_s` is
View SolutionThe earth moves around the Sun in an elliptical orbit as shown in Fig. The ratio `OA//OB=x`. The ratio of the speed of the earth at `B` to that at `A` is nearly
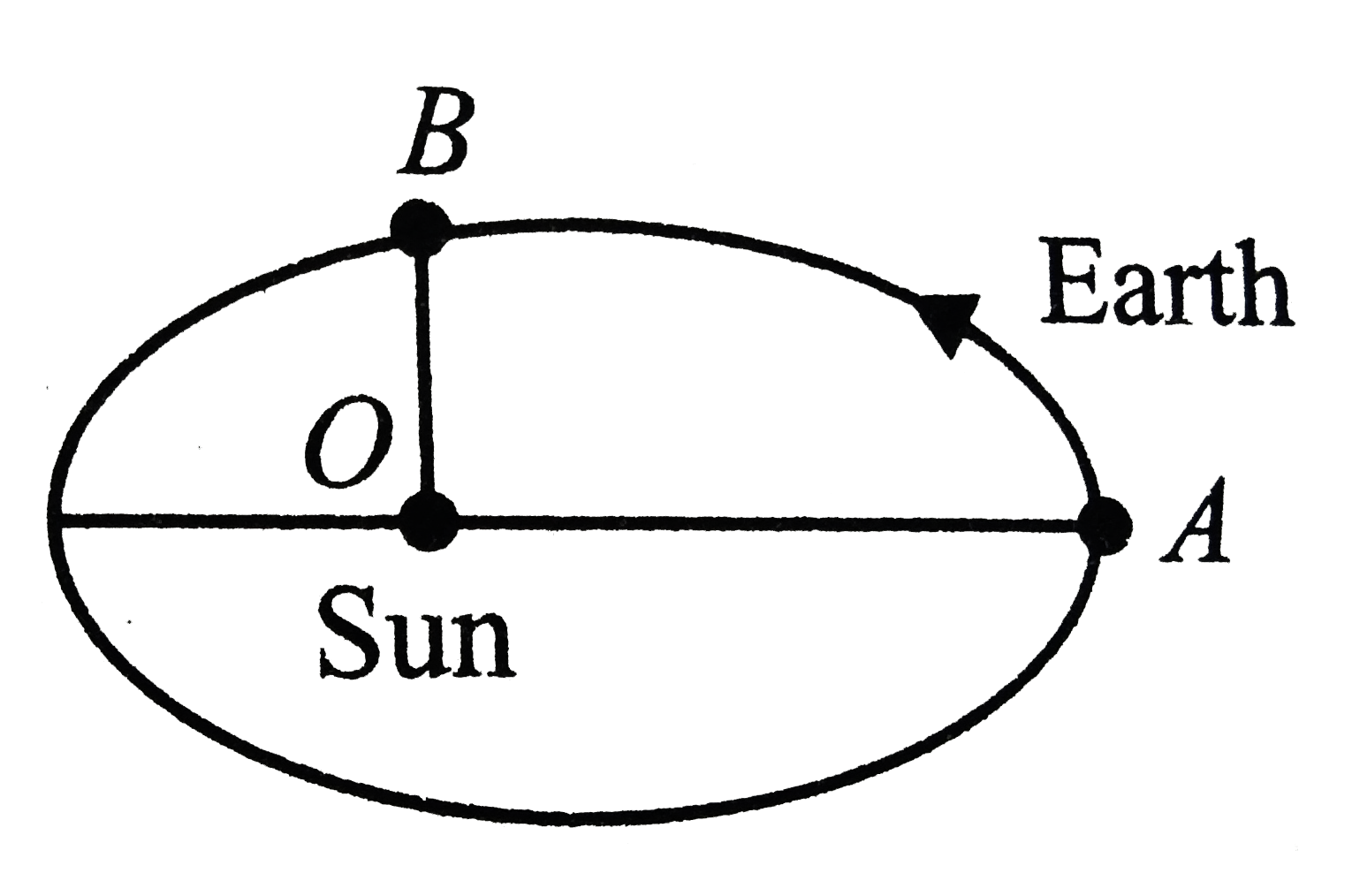
View SolutionThe period of moon's rotation around the earth is approx. 29 days. IF moon's mass were 2 fold its present value and all other things remain unchanged, the period of Moon's rotation would be nearly
View SolutionIf the mass of earth were `2` times the present mass, the mass of the moon were half the present mass and the moon were revolving round the earth at the same present distance, the time period of revolution of the moon would be (in day)
View SolutionTwo sphere of masses `m` and `M` are situated in air and the gravitational force between them is `F`. The space around the masses in now filled with a liquid of specific gravity `3`. The gravitational force will now be
View SolutionThe gravitational force between two bodies is `6.67xx10^(-7) N` when the distance between their centres is `10m`. If the mass of first body is `800 kg`, then the mass of second body is
View SolutionTwo identical spheres each of radius `R` are placed with their centres at a distance `nR`, where `n` is integer greater than `2`. The gravitational force between them will be proportional to
View SolutionA satellite is orbiting around the earth. If both gravitational force and centripetal force on the satellite is `F`, then, net force acting on the satellite to revolve around the earth is
View SolutionMass `M=1` unit is divided into two parts `X` and `(1-X)`. For a given separation the value of `X` for which the gravitational force between them becomes maximum is
View SolutionIf `g` on the surface of the earth is `9.8 m//s^2`, its value at a height of `6400km` is (Radius of the earth `=6400km`)
View SolutionIf `g` on the surface of the earth is `9.8 m//s^2`, its value at a depth of `3200km` is (Radius of the earth `=6400km`) is
View SolutionIf mass of the planet is `10%` less than that of the earth and radius of the planet is `20%` greater than that of the earth then the weight of `40kg` person on that planet is
View SolutionThe angular velocity of the earth with which it has to rotate so that the acceleration due to gravity on `60^@` latitude becomes zero is
View SolutionAssume that the acceleration due to gravity on the surface of the moon is `0.2` times the acceleration due to gravity on the surface of the earth. If `R_e` is the maximum range of a projectile on the earth's surface, what is the maximum range on the surface of the moon for the same velocity of projection
View SolutionThe value of acceleration due to gravity on the surface of earth is `x`. At an altitude of `h` from the surface of the earth, its value is `y`. If `R` is the radius of earth, then the value of `h` is
View SolutionThe point at which the gravitational force acting on any mass is zero due to the earth and the moon system is (The mass of the earth is approximately `81` times the mass of the moon and the distance between the earth and the moon is `3,85,000km`).
View SolutionMasses `2kg` and `8kg` are `18cm` apart. The point where the gravitational field due to them is zero, is
View SolutionParticles of masses `m_1` and `m_2` are at a fixed distance apart. If the gravitational field strength at `m_1` and `m_2` are `vec I_1` and `vec I_2` respectively. Then,
View SolutionThe `PE` of three objects of masses `1kg,2kg` and `3kg` placed at the three vertices of an equilateral triangle of side `20cm` is
View SolutionA small body is initially at a distance `r` from the centre of earth. `r` is greater than the radius of the earth. If it takes `W` joule of work to move the body from this position to another position at a distance `2r` measured from the centre of earth, how many joule would be required to move it from this position to a new position at a distance of `3r` from the centre of the earth.
View SolutionA body of mass 'm' is raised from the surface fo the earth to a height 'nR'(`R`-radius of the earth). Magnitude of the change in the gravitational potential energy of the body is (`g`-acceleration due to gravity on the surface of the earth)
View SolutionA person brings a mass `2kg` from `A` to `B`. The increase in kinetic energy of mass is `4J` and work done by the person on the mass is `-10J`. The potential difference between `B` and `A` is ......`J//kg`
View SolutionThe work done liftting a particle of mass 'm' from the centre of the earth to the surface of the earth is
View SolutionFigure shows two shells of masses `m_(1)` and `m_(2)`. The shells are concentric. At which point, a particle of mass `m` shall experience zero force?
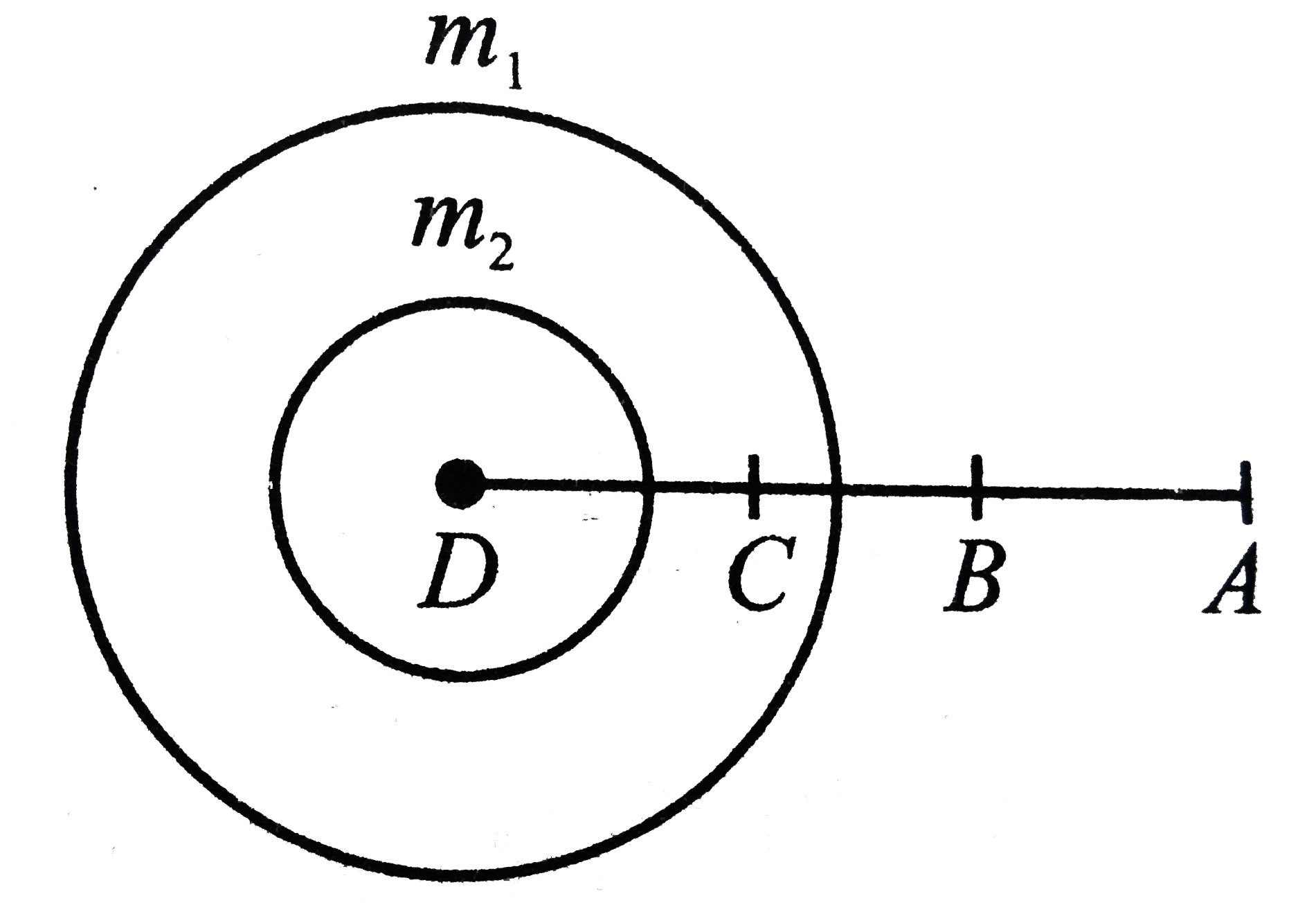
View SolutionEnergy required to move a body of mass m from an orbit of radius 2R to 3R is
View Solutionthe ratio of escape velocities of two planets if `g` value on the two planets are `9.9 m//s^(2)` and `3.3 m//s^(2)` and there are `6400 km` and `3200 km` respectively is
View SolutionThe escape velocity from the surface of the earth of radius `R` and density `rho`
View SolutionA body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
View SolutionA spaceship is launched in to a circular orbit of radius `R` close to surface of earth. The additional velocity to be imparted to the spaceship in the orbit to overcome the earth's gravitational pull is (`g`=acceleration due to gravity)
View SolutionThe escape velocity from the earth is `11 km//s`. The escape velocity from a planet having twice the radius and same density as that of the earth is (in `km//s`)
View SolutionAn object of mass `m` is at rest on earth's surface. Escape speed of this object is `V_(e)`. Same object is orbiting the earth with `h=R`, then escape speed is `V_(e)^(1)`. Then
View SolutionA satellite revolves in a circular orbit with speed, `V=1/(sqrt(3))V_(e)`. If satellite is suddenly stopped and allowed to fall freely onto the earth, the speed with which it hits the earth's surface is
View SolutionA space station is set up in space at a distance equal to the earth's radius from the surface of the earth. Suppose a satellite can be launched from the space station. Let `v_(1)` and `v_(2)` be the escape velocities of the satellite on the earth's surface and space station, respectively. Then
View SolutionThe orbital speed for an earth satellite near the surface of the earth is `7km//sec`. If the radius of the orbit is `4` times the radius of the earth, the orbital speed would be
View SolutionTwo satellite are revolving round the earth at different heights. The ratio of their orbital speeds is `2:1`. If one of them is at a height of the other satellite is (in `km`)
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionTwo satellites `M` and `N` go around the earth in circular orbits at heights of `R_(M)` and `R_(N)` respectively from the surrface of the earth. Assuming the earth to be a uniform sphere of radius `R_(E)`, the ratio of velocities of the satellites `(V_(M))/(V_(N))` is
View SolutionA satellite of mass `m` revolves revolves round the earth of mass `M` in a circular orbit of radius `r` with an angular velocity `omega`. If the angular velocity is `omega//8` then the radius of the orbit will be
View SolutionThe moon revolves round the earth `13` times in one year. If the ratio of sun-earth distance to earth-moon distance is `392`, then the ratio of masses of sun and earth will be
View SolutionA satellite is launched into a circular orbit of radius `R` around the earth. While a second is lunched into an orbit of radius `1.01R` The period of the second satellite is longer than the first one by approximately:
View SolutionAn astronaut orbiting in a spaceship round the earth has a centripetal acceleration of `2.45 m//s^(2)`. The height of spaceship from earth's surface is (`R`=radius of earth)
View SolutionA satellite moves around the earth in a circular orbit with speed `v`. If `m` is the mass of the satellite, its total energy is
View SolutionThe `K.E.` of a satellite in an orbit close to the surface of the earth is `E`. Its max `K.E.` so as to escape from the gravitational field of the earth is
View SolutionTwo satellite of masses `400 kg,500kg` are revolving around earth in different circular orbits of radii `r_(1),r_(2)` such that their kinetic energies are equal. The ratio of `r_(1)` to `r_(2)` is
View SolutionThe kinetic energy needed to project a body of mass m from the earth's surface to infinity is
View SolutionOrbital speed of geo-stationary satellite is
View Solution
LEVEL I(C.W.) questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example