Complete Solutions to LEVEL-VI of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | LEVEL-VI |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Find the potential energy of the gravitational interaction of a point mass `m` and a rod of mass `m` and length `l`, if they are along a straight line. Point mass is at a distance of a from the end of the rod.

Find the potential energy of the gravitational
View SolutionMass `M` is distributed uniformly along a line of length `2L`. A particle of mass `m` is at a point that is at a distance `a` above the centre of the line on the its perpendicular bisector (Point `P` in figure). The gravitational force that the line exert on the particle is
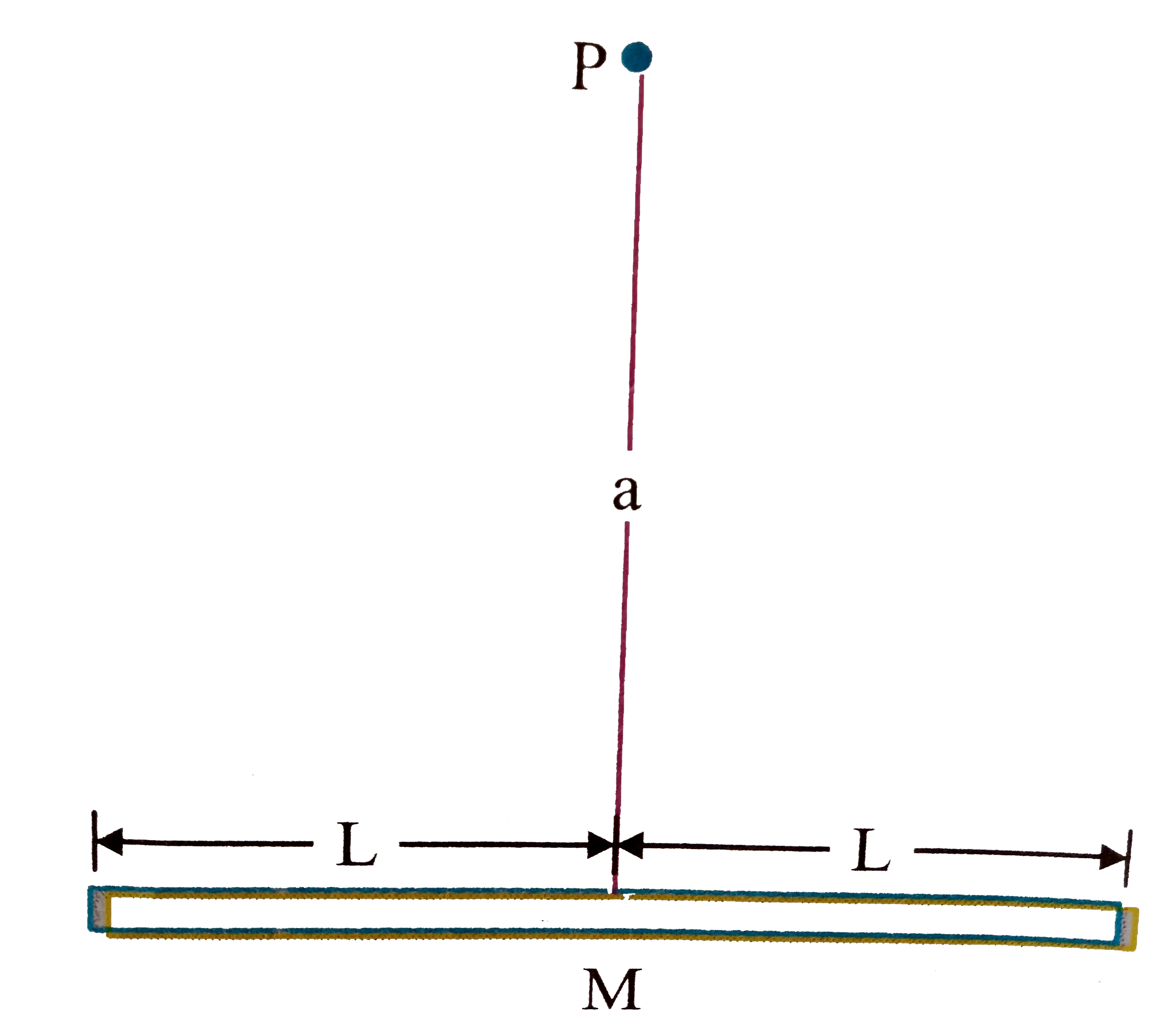
View SolutionA planet of mass `m` moves along an ellipse around the sun so that its maximum and minimum distance from the sun are equal to `r_(1)` and `r_(2)` respectively. Find the angular momentum of this planet relative to the centre of the sun. mass of the sun is `M`.
View SolutionInside a uniform sphere of density `rho` there is a spherical cavity whose centre is at a distance `l` from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View SolutionInside a fixed sphere of radius `R` and uniform density `rho`, there is spherical cavity of radius `(R )/(2)` such that surface of the cavity passes through the centre of the sphere as shown in figure. A particle of mass `m_(0)` is released from rest at centre `B` of the cavity. Calculate velocity with which particle strikes the centre `A` of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.

View SolutionA ring of radius `R = 4m` is made of a highly dense material. Mass of the ring is `m_(1) = 5.4 xx 10^(9) kg` distributed uniformly over its circumference. A highly dense particle of mass `m_(2) = 6 xx 10^(8) kg` is placed on the axis of the ring at a distance `x_(0) = 3 m` from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionA cosmic body `A` moves to the sun with velocity `v_(0)`(when far from the sun) and aiming parameter `l`, the arm of the vector `v_(0)`, relative to the centre of the sun. find the minimum distance by which this body will get to the sun. mass of the sum is `M`.
View SolutionTwo satellite `S_(1)` and `S_(2)` revolve around a planet in coplanar circular orbits in the opposite sense. The periods of revolutions are `T` and `eta T` respectively. Find the angular speed of `S_(2)` as observed by an astronouts in `S_(1)`, are observed by an astronaut in `S_(1)`, when they are closest to each other.
View SolutionA particle of mass `m` is placed on centre of curvature of a fixed, uniform semi-circular ring of radius `R` and mass `M` as shown in figure. Calculate:
(a) interaction force between the ring and the particle and
(b) work required to displace the particle from centre of curvature to infinity.

View SolutionGiven a thin homogenous disc of radius a and mass `m_(1)`. A particle of mass `m_(2)` is placed at a distance `l` from the disc on it's axis of symmetry. Initially both are motionless in free space but they ultimately collide because of gravitational attraction. find the relative velocity at the time of collision. assume `altlt1`.
View SolutionThe density of the core a planet is `rho_(1)` and that of the outer shell is `rho_(2)`. The radii of the core and that of the planet are `R` and `2R` respectively. The acceleration due to gravity at the surface of the planet is same as at a depth `R`. Find the ratio of `(rho_(1))/(rho_(2))`

View SolutionA projectile of mass `m` is fired from the surface of the earth at an angle `alpha = 60^(@)` from the vertical. The initial speed `upsilon_(0)` is equal to `sqrt((GM_(e))/(R_(e))`. How high does the projectile rise ? Neglect air resistance and the earth's rotation.
View Solutionfind the velocity of a satellite travelling in an elliptical orbit, when it reaches point `C`, at the end of the semi-minor axis.

View SolutionIn astronomy order of magnitude estimation plays an important role. The derivative `(dp)/(dt)` can be taken difference ration `(DeltaP)/(Deltar)`. Consider the star has a radius `R`, pressure at its centre is `P_(e)` and pressure at outer layer is zero is the average mass is `(M_(Q))/2` and average radius `(R_(o))/2` then the expression for `P_(c)` is
View SolutionA narrow tunnel is dug across a planet diametrically and a small body is dropped from a large height, so that it falls into the tunnel. The variation of its kinetic energy `(KE)` with distance `(r)` from the centre is represented by
View Solution_S01_027_Q01.png)
If the law of gravitation be such that the force of attraction between two particles vary inversely as the `5//2^(th)` power of their separation then the graph of orbital velocity `v_(0)` plotted against the distance `r` of a satellite from the earth's centre on a log-log scale is shown alongside the slope on a line will be
View SolutionA small satellite revolves around a heavy planet in a circular orbit. At a point in its orbit an impulse acts suddenly and instantaneously increases its kinetic energy `K` times without change in its direction of motion. The ratio of maximum to the minimum distance from the planet is [Assume mass of satellite is negligible small compared to that of planet]
View SolutionA satellite is orbiting around the earth in an orbitin equatorial plane of radius `2R_(e)` where `R_(e)` is the radius of earth. Find the area on earth, this satellite covers for communication purpose in its complete revolution.
View SolutionA planet moves aruond the sun in an elliptical orbit such that its kinetic energy is `K_(1)` and `K_(2)` when it is nearest to the sun and farthest from the sun respectively. The smallest distance and the largest distance between the planet and the sun are `r_(1)` and `r_(2)` respectively.
View SolutionA smooth tunnel is dug along the radius of the earth that ends at the centre. A ball is released from the surface of earth along the tunnel. If the coefficient of restitution is `0.2` between the surface and ball, then the distance travelled by the ball before second collision at the centre is
View SolutionA cannon shell is fired to hit a target at a horizontal distance `R`. However, it breaks into two equal parts at its highest point. One part `A` returns to the cannon. The other part is:
View SolutionA particle moving with kinetic energy `3J` makes an elastic head-on collision with a stationary particle which has twice its mass. During the impact :-
View SolutionConsider `a` thin spherical shell of uniform density of mass `M` and radius `R`:
View SolutionA satellite moves in an elliptical orbit about the earth. The minimum and maximum distance of the satellite from the centre of earth are `7000 km` and `8750 km` respectively. For this situation, mark the correct statements (s). [Take `M_(e)=6xx10^(24) kg`]
View SolutionThe gravitational potential change uniformly from `-20 J//kg` to `-40J//kg` as one moves along `X`-axis from `x=-1m` to `x=+1m`. Mark the correct statement (s) about gravitational field intensity of origin.
View SolutionConsider two satellites `A` and `B` of equal mass `m`, moving in the same circular orbit about the earth, but in the opposite sense as shown in Fig. The orbital radius is `r`. The satellites undergo a collision which is perfectly inelastic. For this situation, mark out the correct statement(s). [Take mass of earth as `M`]

View Solution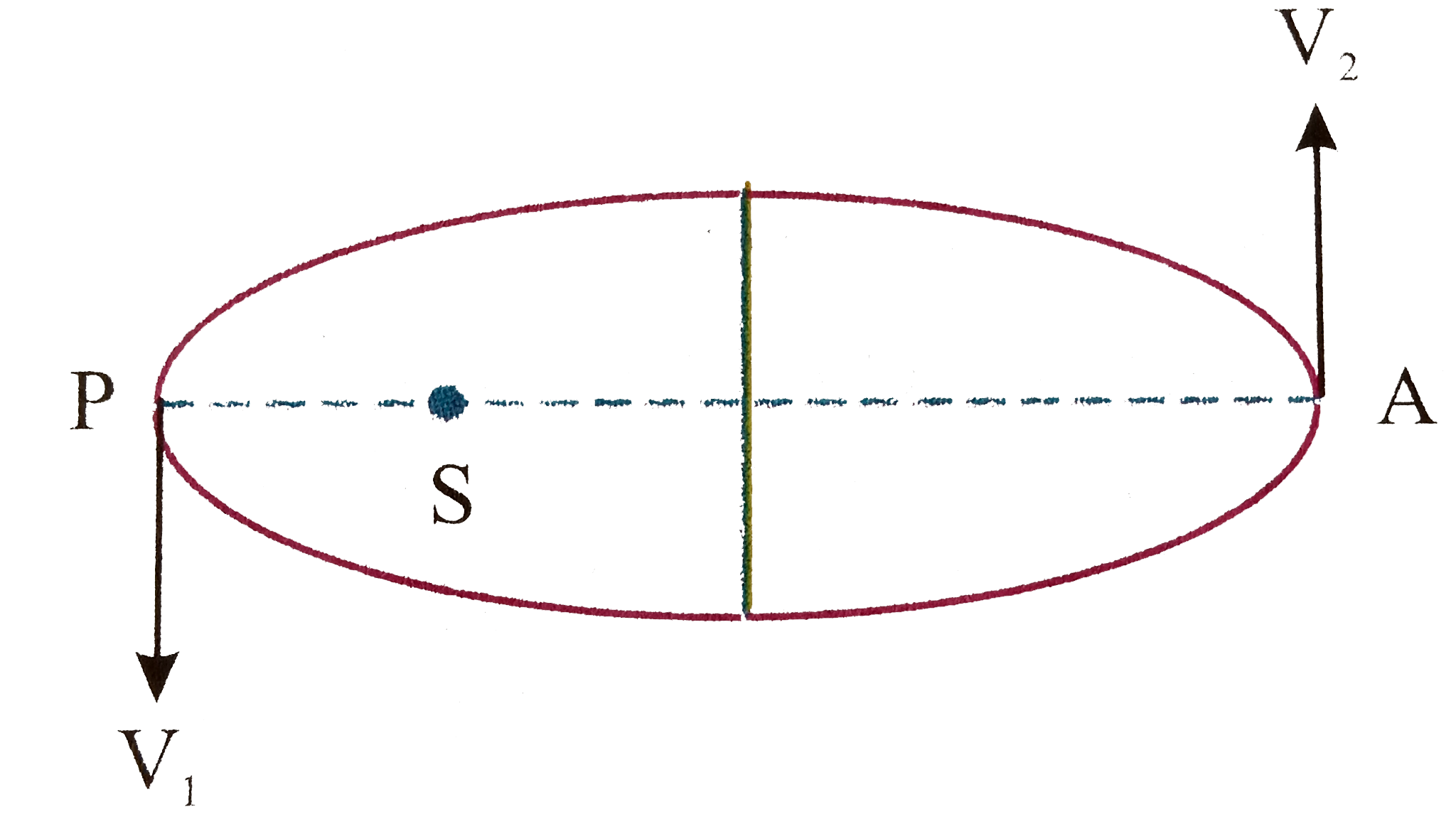
A planet of mass `m` is moving in an elliptical orbit around the sun of mass `M`. The semi major axis of its orbit is a, eccentricity is `e`.
Find speed of planet `V_(1)` at perihelion `P`
View Solution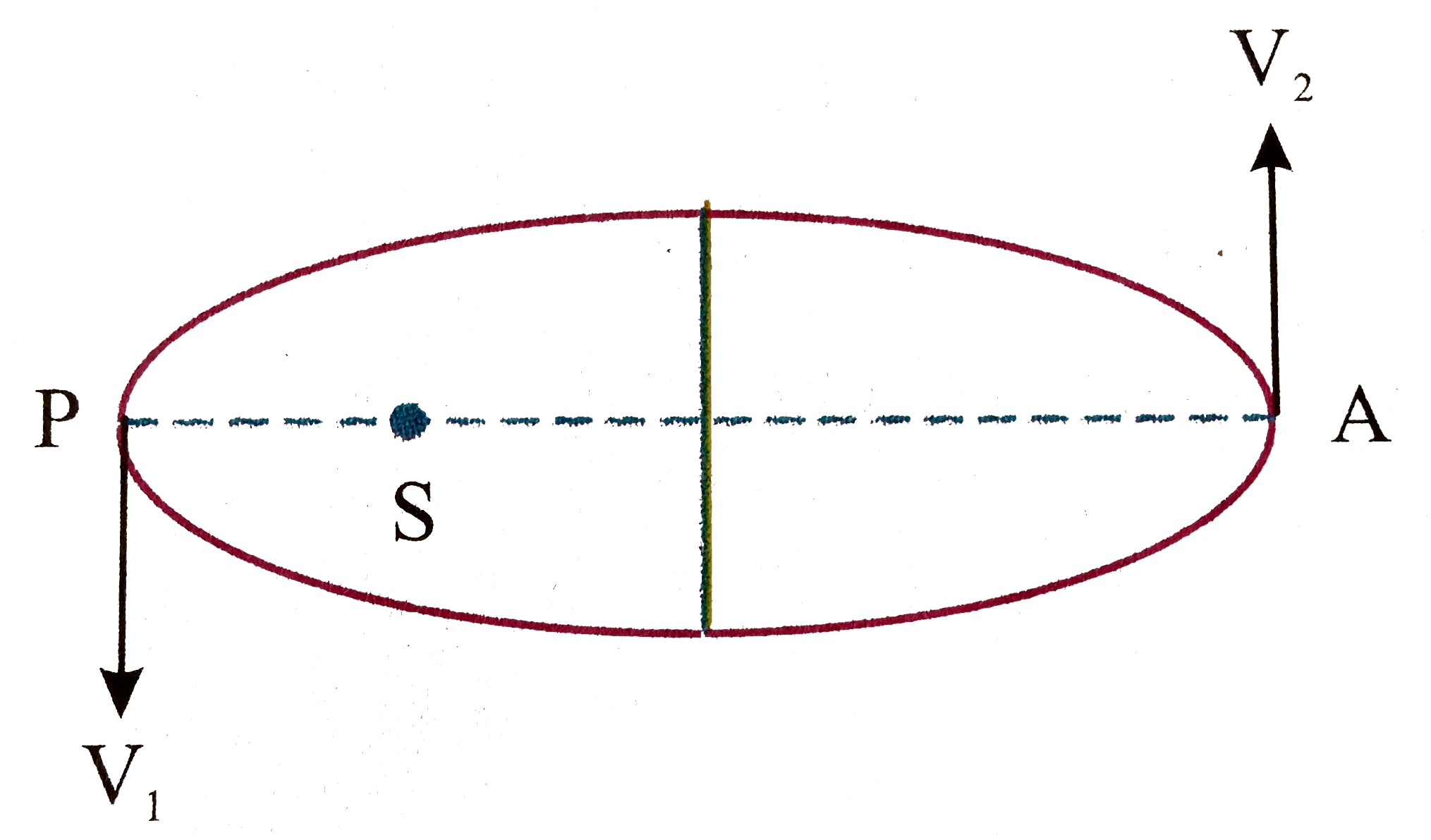
A planet of mass `m` is moving in an elliptical orbit around the sun of mass `M`. The semi major axis of its orbit is a, eccentricity is `e`.
Find speed of planet `V_(2)` at aphelion `A`.
View Solution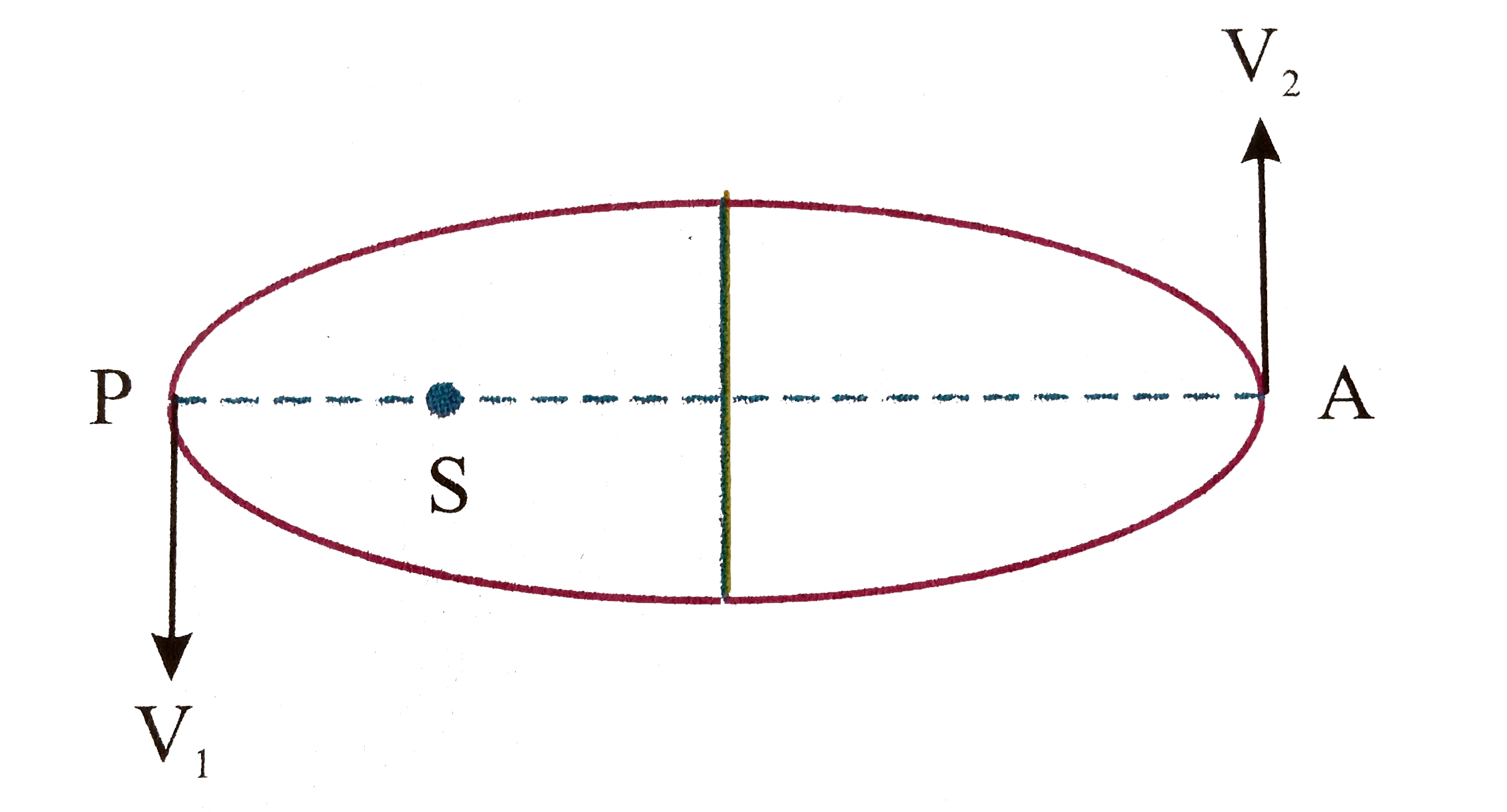
A planet of mass `m` is moving in an elliptical orbit around the sun of mass `M`. The semi major axis of its orbit is a, eccentricity is `e`.
Find total energy of planet interms of given parameters.
View Solution
Sphere of mass `M` and radius `R` is surrounded by a spherical shell of mass `2M` and radius `2R` as shown. A small particle of mass `m` is released from rest from a height `h(lt ltR)` above the shell. There is hole in the shell.
In what time will it enter the hole at `A`?
View Solution
Sphere of mass `M` and radius `R` is surrounded by a spherical shell of mass `2M` and radius `2R` as shown. A small particle of mass `m` is released from rest from a height `h(ltltR)` above the shell. There is hole in the shell.
What time will it take to move from `A` to `B`?
View Solution
Sphere of mass `M` and radius `R` is surrounded by a spherical shell of mass `2M` and radius `2R` as shown. A small particle of mass `m` is released from rest from a height `h(ltltR)` above the shell. There is hole in the shell.
With what approximate speed will it collide at `B`?
View Solution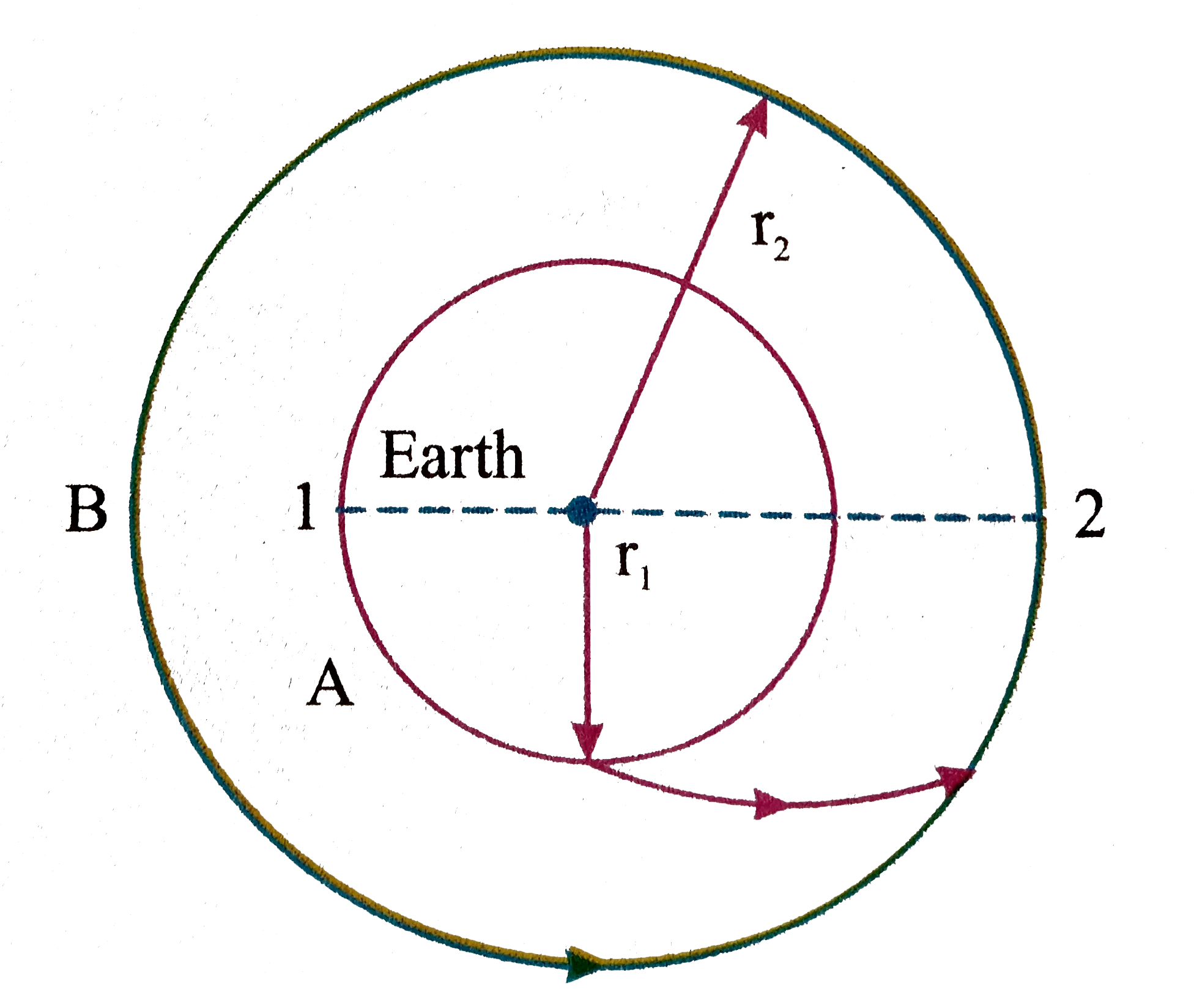
Two satellites `A` and `B` are revolving around the earth in circular orbits of radius `r_(1)` and `r_(2)` respectively with `r_(1)ltr_(2)`. Plane of motion of the two are same. At position `1`, `A` is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet `B` at position `2` as shown. focal lengths of the elliptical path are `r_(1)` and `r_(2)` respectively. at position `2`, `A` is given another impulse so that velocities of `A` and `B` at `2` become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as `T^(2)alphar^(3)` where a is semi-major axis of the ellipse which is `(r_(1)+r_(2))/2` in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
When `A` is given its first impulse at that moment
View Solution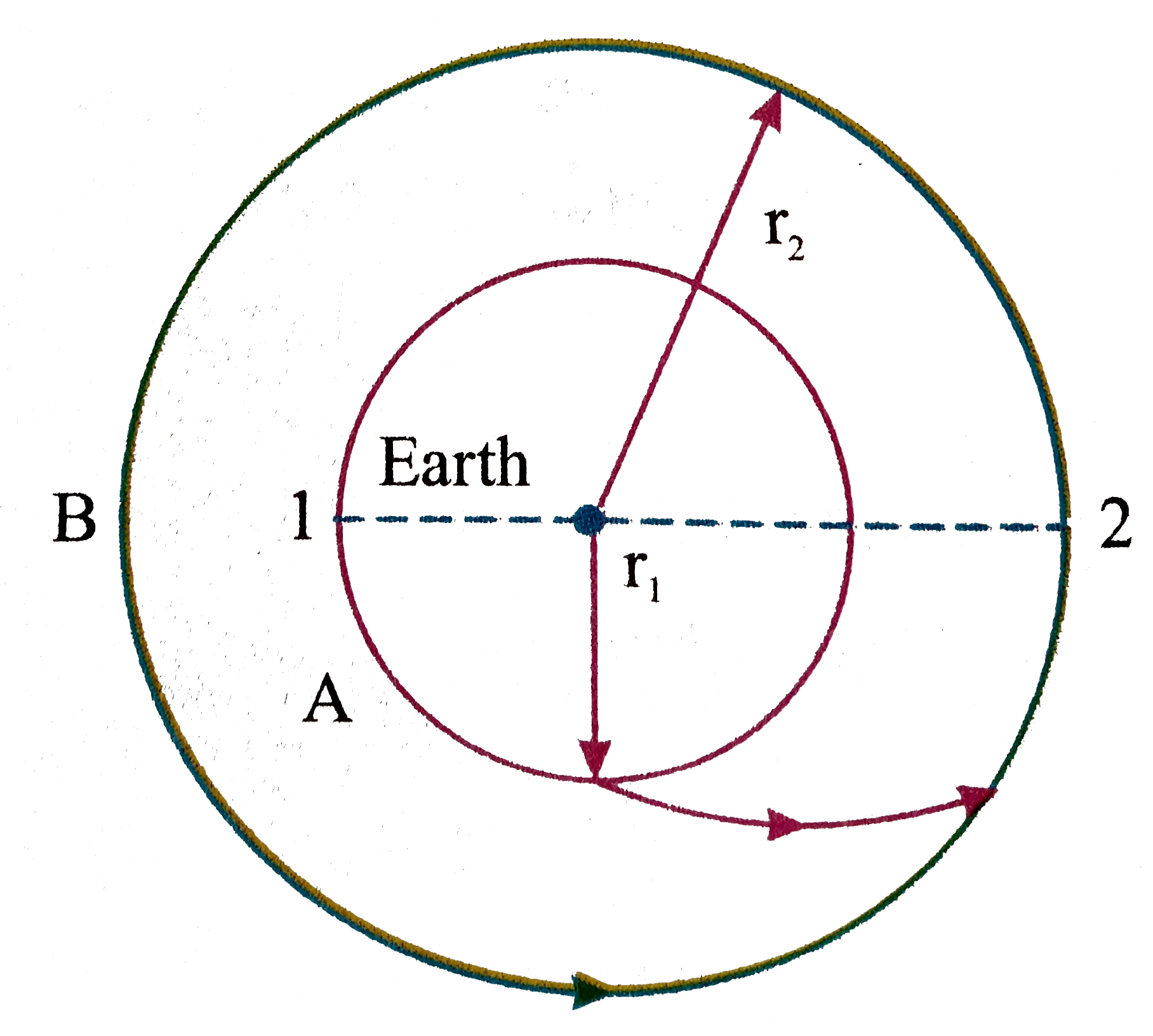
Two satellites `A` and `B` are revolving around the earth in circular orbits of radius `r_(1)` and `r_(2)` respectively with `r_(1)ltr_(2)`. Plane of motion of the two are same. At position `1`, `A` is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet `B` at position `2` as shown. focal lengths of the elliptical path are `r_(1)` and `r_(2)` respectively. at position `2`, `A` is given another impulse so that velocities of `A` and `B` at `2` become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as `T^(2)alphar^(3)` where a is semi-major axis of the ellipse which is `(r_(1)+r_(2))/2` in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If the two have same mass
View Solution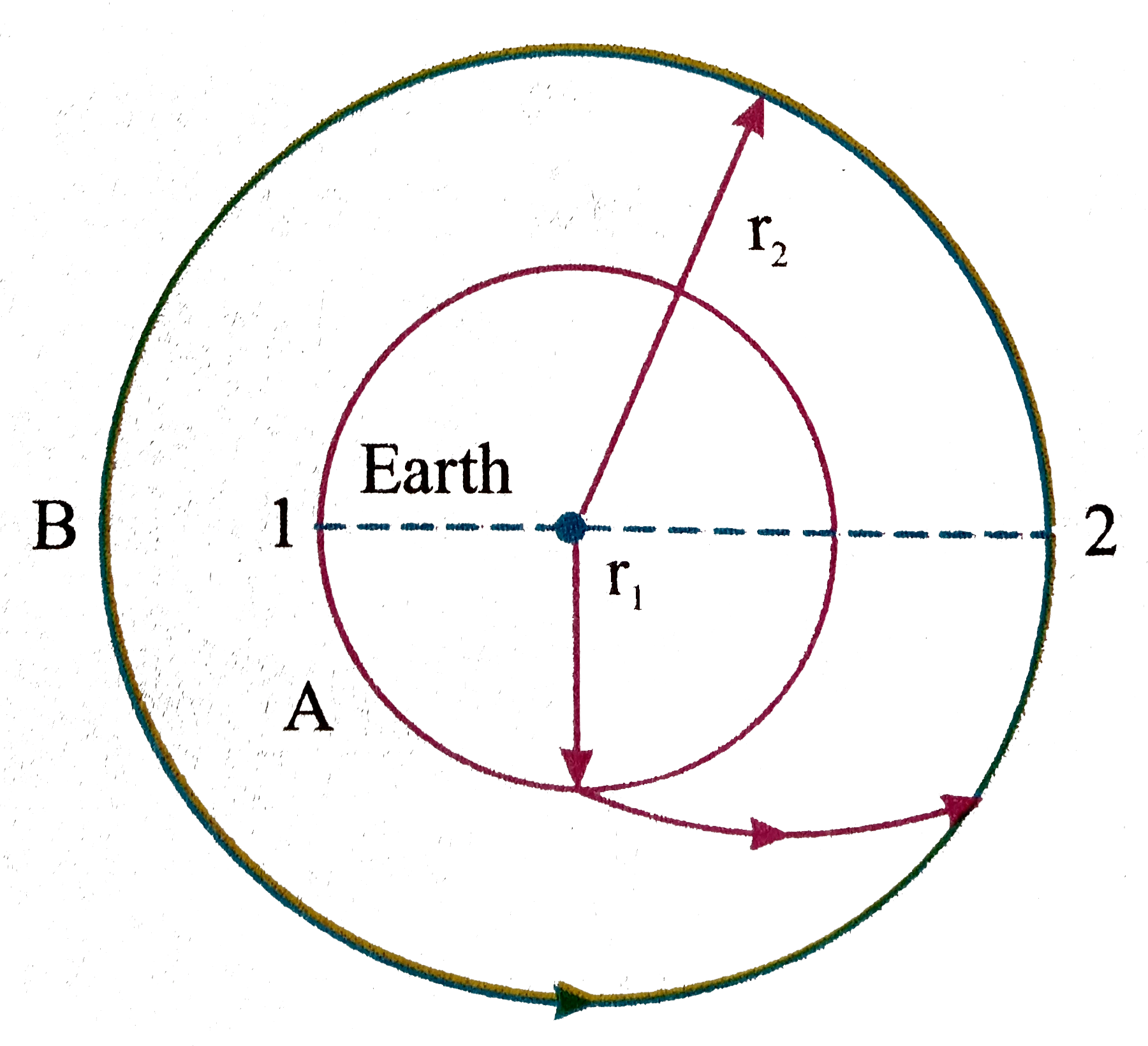
Two satellites `A` and `B` are revolving around the earth in circular orbits of radius `r_(1)` and `r_(2)` respectively with `r_(1)ltr_(2)`. Plane of motion of the two are same. At position `1`, `A` is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet `B` at position `2` as shown. focal lengths of the elliptical path are `r_(1)` and `r_(2)` respectively. at position `2`, `A` is given another impulse so that velocities of `A` and `B` at `2` become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as `T^(2)alphar^(3)` where a is semi-major axis of the ellipse which is `(r_(1)+r_(2))/2` in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If `r_(2)=3r_(1)` and time period of revolution for `B` be `T` then time taken by `A` in moving from position `1` to position `2` is
View SolutionA mass of `6xx10^(24) kg` is to be compressed in a sphere in such a way that the escape velocity from its surface is `3xx10^(8) m//s`. Find the radius of the sphere (in `mm`).
View SolutionTwo equal masses are held at a distance of `3.0cm` in a line and released simulataneously. What will be the separation between them after `2s`?
View SolutionTwo satellites `S_(1)` and `S_(2)` are to be set in the orbits of `R/4` and `R/6` above the earth's surface. They revolve around the earth in a coplanar circular orbit in the opposite sense. What will be the ratio of speeds of projection from the earth's surface?
View SolutionDistance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` and their radii `a` and `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of `G`, `M` and `a`.
View SolutionTwo particles `A` and `B` of masses `1kg` and `2kg`, respectively, are kept at a very large separation. When they are released, they move under their gravitational attraction. Find the speed (in `10^(-5) m//s`) of `A` when that of `B` is `3.6 cm//hr`.
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed of equal to half the magnitude of escape velocity from earth.
(i). Determine the height of the satellite above the earth's surface
(ii). If the satellite is stopped suddenly in its orbit and allowed to fall freely on the earth. Find the speed with it hits and surface of earth. Given `M="mass of earth & R "="Radius of earth"
View SolutionA larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for `m =k((M)/(288)).` The value of k is
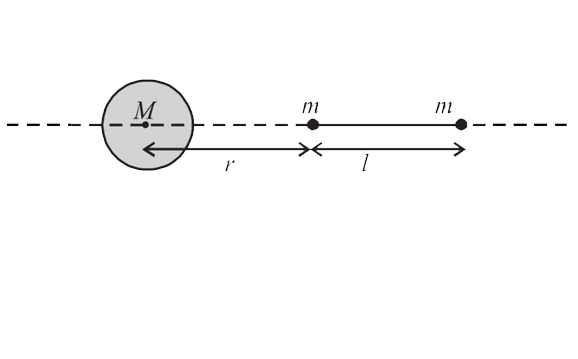
View Solution
LEVEL-VI questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example