Complete Solutions to LEVEL III of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | LEVEL III |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
A point mass is orbiting a significant mass `M` lying at the focus of the elleptical orbit having major and minor axes given by `2a` and `2b` respectively. Let `r` be the distance between the mass `M` and the point of major axis. The velocity of the particle can be given as
View SolutionA planet of mass `m` revolves in elliptical orbit around the sun of mass `M` so that its maximum and minimum distance from the sun equal to `r_(a)` and `r_(p)` respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA satellite moving in an elliptical orbit around the earth as shown. The minimum and maximum distance of the satellite from earth are `3` units and `5` units respectively. The distance of satellite from earth when it is at `P` is .........unit

View SolutionThe longest and the shortest distance of a planet from the sun are `R_(1)` and `R_(2)`. Distances from sun when it is normal to major axis of orbit is
View SolutionA satellite is orbiting just above the surface of a planet of average density `D` with period `T`. If `G` is the universal gravitational constant, the quantity `(3pi)/G` is equal to
View SolutionA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the end of the minor axis and close to the sun is
View SolutionAn artificial satellite revolves around the earth in circular orbit of radius `r` with time period `T`. The satellite is made to stop in the orbit which makes it fall onto the earth. Time of fall of the satellite onto the earth is given by
View SolutionA homogeneous spherical heavenly body has a uniform and very narrow frictionless duct along its diameter. Let mass of the body be `M` and diameter be `D`. A point mass `m` moves smoothly inside the duct. Force exerted on this mass when it is at a distance `s` from the centre of the body is (numerically)
View SolutionTwo concentric shells of different mass `m_(1)` and `m_(2)` are having a sliding particle of mass `m`. The forces on the sliding at positions `I,II ` and `III` are respectively

View SolutionSuppose a vertical tunnel is dug along the diameter of earth , which is assumed to be a sphere of uniform mass density `rho`. If a body of mass `m` is thrown in this tunnel, its acceleration at a distance `y` from the centre is given by

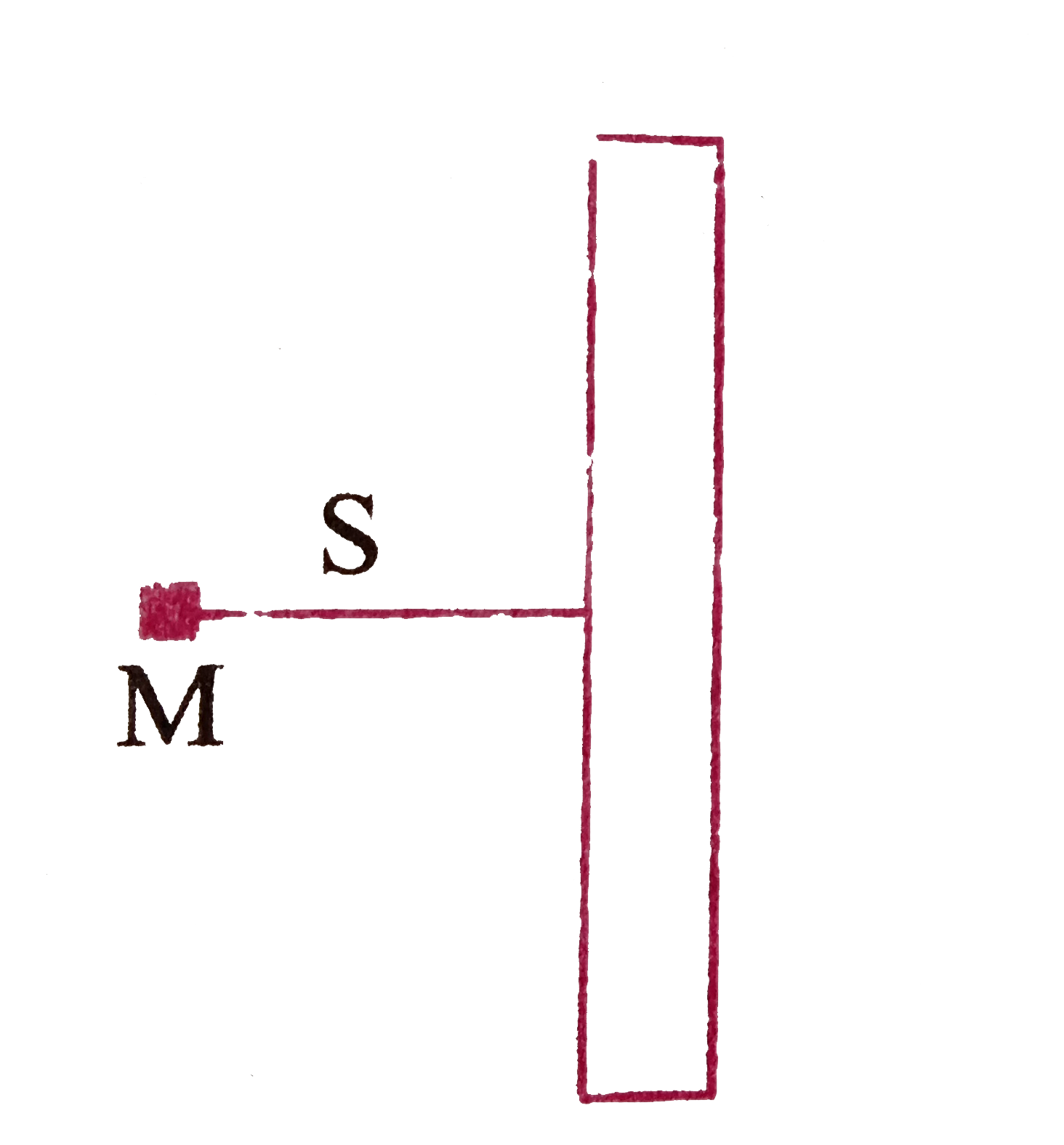
View SolutionA point mass `M` is at a distance `S` from an infinitely long and thin rod of linear density `D`. If `G` is the gravitational constant then gravitational force between the point mass and the rod is
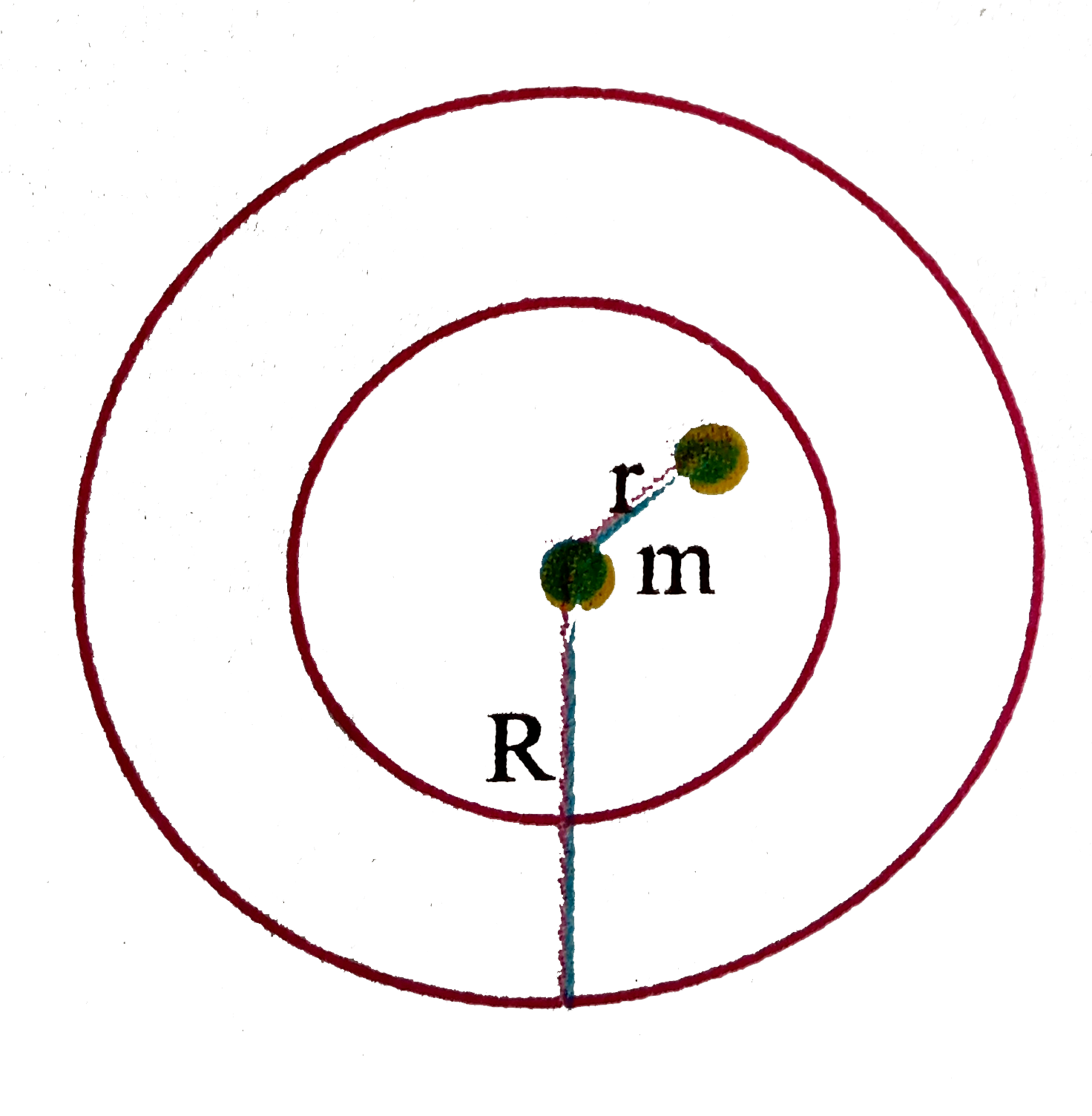
View SolutionA cavity of radius `R//2` is made inside a solid sphere of radius `R`. The centre of the cavity is located at a distance `R//2` from the centre of the sphere. The gravitational force on a particle of a mass `'m'` at a distance `R//2` from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here `g=GM//R^(2)`, where `M` is the mass of the solide sphere]
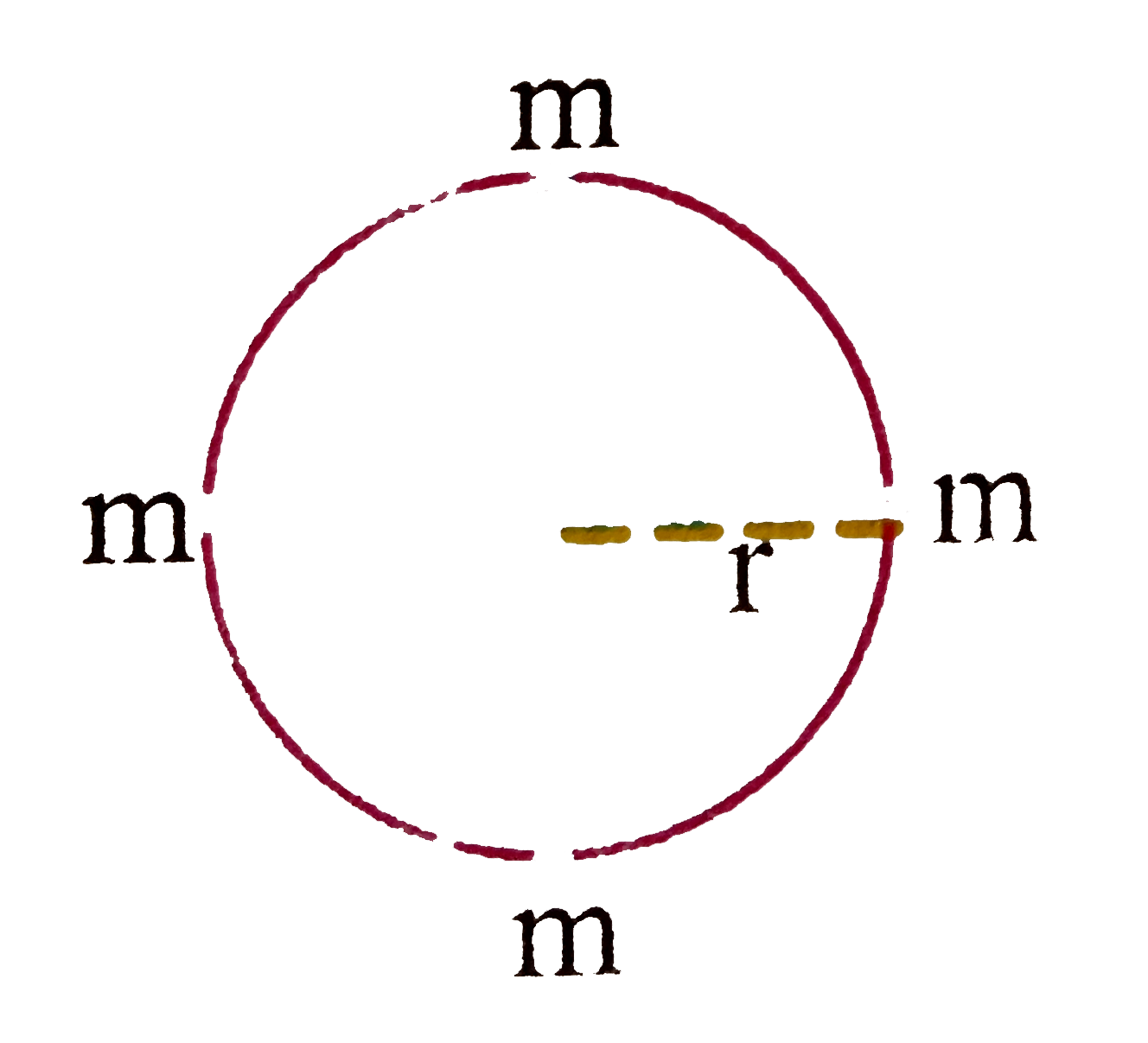
View SolutionFour masses 'm' each are orbitinting in a circular of radius `r` in the same direction under gravitational force. Velocityof each particle is
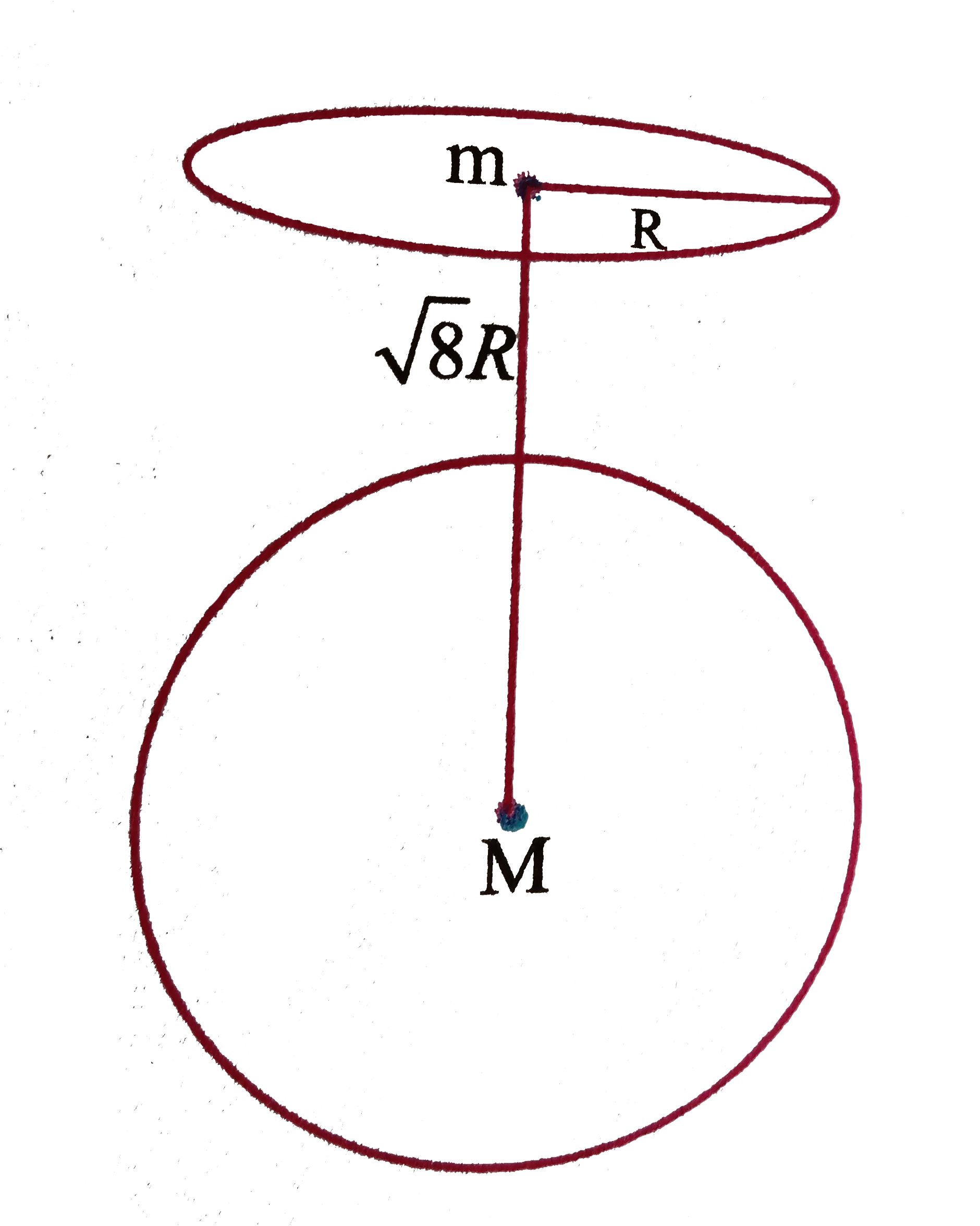
View SolutionThe centres of a ring of mass `m` and a sphere of mass `M` of equal radius `R`, are at a distance `sqrt(8) R` apart as shown. The force of attraction between the ring and the sphere is
View SolutionA mass `m` extends a vertical helical spring of spring constant `k` by `xm` at the surface of the earth. Extension in spring by the same mass at height `h` meter above the surface of the earth is
View SolutionA straight rod of length `L` extends from `x=a` to `x=L+a`. Find the gravitational force exerts on a point mass `m` at `x=0` is (if the linear density of rod`mu=A+Bx^(2)`)
View SolutionA mass `m` is placed in the cavity inside hollow sphere of mass `M` as shown in the figure. The gravitational force on `m` is
View SolutionA spherical shell is cut into two pieces along a chord as shown in the figure. `P` is a point on the plane of the chord. The gravitational field at `P` due to the upper part is `I_(1)`, and that due to the lower part is `I_(2)`. What is the relation between them?

View SolutionThe magnitudes of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `E_(1)` and `E_(2)` respectively. Then:
View SolutionTwo masses `90kg` and `160 kg` are `5m` apart. The gravitational field intensity at a point `3m` from `90kg` and `4m` from `160 kg` is
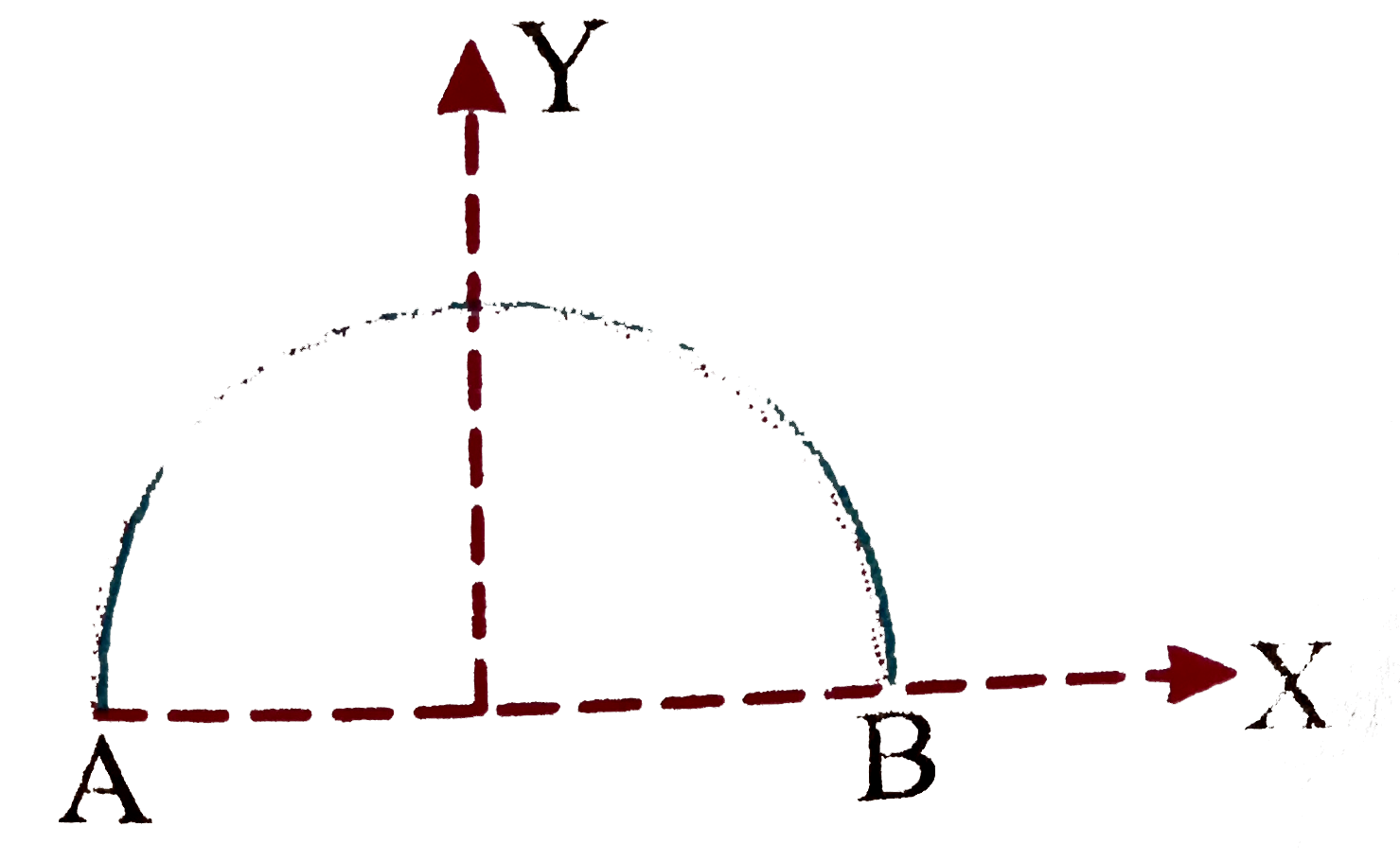
View SolutionGravitational field intensity at the centre of the semi circle formed by a thin wire `AB` of mass `m` and length `L` is
View SolutionTwo equal masses each `m` are hung from a balance whose scale pans differ in vertical height by `h`. The error in weighing is
View SolutionIf earth were to rotate on its own axis such that the weight of a person at the equator becomes half the weight at the poles, then its time period of rotation is (g = acceleration due to gravity near the poles and R is the radius of earth) (Ignore equatorial bulge)
View SolutionFour particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
View SolutionThe gravitational potential of two homogeneous spherical shells `A` and `B` of same surface density at their respective centres are in the ratio `3:4`. If the two shells collapse into a single one such that surface charge density remains the same, then the ratio of potential at an internal point of the new shell to shell `A` is equal to
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

View SolutionThe gravitational force in a region is given by, `vec(F)=ayhati+axhatj`. The work done by gravitational force to shift a point mass `m` from `(0,0,0)` is `(x_(0),y_(0),z_(0))` is
View SolutionTwo identical thin ring each of radius `R` are co-axially placed at a distance `R`. If the ring have a uniform mass distribution and each has mass `m_(1)` and `m_(2)` respectively, then the work done in moving a mass `m` from the centre of one ring to that of the other is :
View SolutionThe gravitational field in a region due to a certain mass distribution is given by `vec(E)=(4hati-3hatj)N//kg`. The work done by the field in moving a particle of mass `2kg` from `(2m,1m)` to `(2/3m,2m)` along the line `3x+4y=10` is
View SolutionA particle of mass `1kg` is placed at a distance of `4m` from the centre and on the axis of a uniform ring mass `5kg` and radius `3m`. The work done to increase the distance of the particle from `4m` to `3sqrt(3)`m is
View SolutionConsider two configurations of a system of three particles of masses `m`, `2m` and `3m`. The work done by gravity in changing the configuration of the system from figure (i) to figure (ii) is

View SolutionA ring having non-uniform distribution of mass `M` and radius `R` is being considered. A point mass `m_(0)` is taken slowly towards the ring. In doing so, work done by the external force against the gravitational force exerted by ring is

View SolutionTwo concentric spherical shells `A` and `B` of radii `R` and `2R` and mases `4M`, and `M`, respectively are placed in space as shown in Fig. The gravitational potential at `P` at a disatnce `r(R lt r lt 2R)`from the centre of shells is

View SolutionThe potential energy of body of mass `m` given by `U=px+qy+rz`. The magnitude of the acceleration of the body will be
View SolutionA particle is placed in a field characterized by a value of gravitational potential given by `V=-kxy`, where `k` is a constant. If `vec(E)_(g)` is the gravitational field then
View SolutionA thin rod of length `L` is bent to form a semi circle. The mass of the rod is `M`. What will be the gravitational potential at the centre of the circle?
View SolutionIf the gravitational field intensity at a point is given by `g = (GM)/(r^(2.5))`. Then, the potential at a distance `r` is
View SolutionIn a certain region of space, the gravitational field is given by `-k//r`, where `r` is the distance and `k` is a constant. If the gravitational potential for the gravitational potential `V`?
View SolutionDistance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` and their radii `a` and `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of `G`, `M` and `a`.
View SolutionThere is crater of depth `R//100` on the surface of the moon (raduis `R`). A projectile is fired vertically upwards from the crater with a velocity, which is equal to the escape velocity `v` from the surface of the moon. The maximum height attained by the projectile, is :
View SolutionGraviational acceleration on the surface of plane fo `(sqrt6)/(11)g.` where g is the gracitational acceleration on the surface of the earth. The average mass density of the planet is `(2)/(3)` times that of the earth. If the escape speed on the surface of the earht is taken to be `11 kms^(-1)` the escape speed on teh surface of the planet in `kms^(-1)` will be
View SolutionTwo spherical planets P and Q have the same uniform density `rho,` masses `M_p and M_Q` and surface areas A and 4A respectively. A spherical planet R also has uniform density `rho` and its mass is `(M_P + M_Q).` The escape velocities from the plantes P,Q and R are `V_P V_Q and V_R` respectively. Then
View SolutionA spherically symmetric gravitational system of particles has a mass density` rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):}` where`rho_0` is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce `r(0ltrltOO)` form the centre of the system is represented by
View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
View Solution
LEVEL III questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example