Complete Solutions to LEVEL-V of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | LEVEL-V |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
A spherical hollow is made in a lead sphere of radius `R` such that its surface touches the outside surface of the lead sphere and passes through the centre. The mass of the lead sphere before hollowing was `M`. The force of attraction that this sphere would exert on a particle of mass `m` which lies at a distance `d` from the centre joining the centre of the sphere and the hollow is
View SolutionA thin rod of mass `M` and length `L` is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass `m` at the centre of curvature?
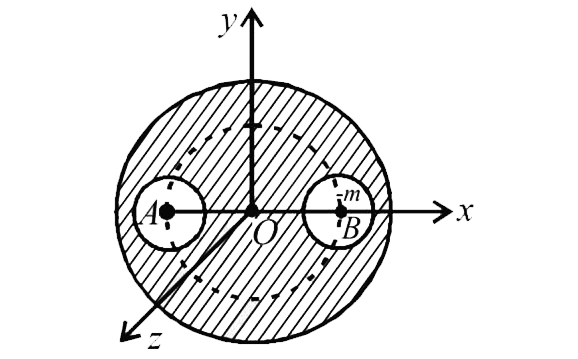
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionThe gravitational potential due to earth at infinite distance from it is zero. Let the gravitational potential at a point `P` be `-5 J kg^(-1)`. Suppose, we arbitrarily assume the gravitational potential at infinity to be `+10 J kg^(-1)`, then the gravitational potential at `P` will be
View SolutionA body starts from rest from a point distant `r_(0)` from the centre of the earth. It reaches the surface of the earth whose radius is `R`. The velocity acquired by the body is
View SolutionTwo rings having masses `M` and `2M` respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point `P` is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point `P` is
View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `R`, at a distance `2R` from its centre `O`. A small particle starts from `P` and reaches `O` under gravitational attraction only. Its speed at `O` will be
View SolutionThe gravitational field due to a mass distribution is given by `E=K/x^3` in X-direction. Taking the gravitational potential to be zero at infinity, find its value at a distance x.
View SolutionAn artificial satellite of the earth is launched in circular orbit in the equatorial plane of the earth and the satellite is moving from west to east. With respect to a person on the equator, the satellite is completing one round trip in `24 h`. Mass of the earth is `M=6xx10^(24)kg.`For this situation the orbital radius of the satellite is
View SolutionA satellite is orbiting around earth in a circular orbit of radius `r`. A particle of mass `m` is projected from satellite in forward direction with velocity `v=sqrt(2/3)` times orbital velocity (this velocity is with respect to the earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
View SolutionA satellite moving in an elliptical orbit around the earth as shown. The minimum and maximum distance of the satellite from earth are `3` units and `5` units respectively. The distance of satellite from earth when it is at `P` is .........unit

View SolutionAn exploratory rocket of mass `m` is an orbit about the sun at radius of `R_(ES)//10` (one tenth of the radius of the earth's orbit about the sun). To exit this orbit, it fires its engine over a short period of time. This quickly doubles the velocity of the rocket while halving its mass the burn, what is the kinetic energy of the rocket? take mass of sun as `M_(S)`
View SolutionA shell is fired vertically from the earth with speed `v_(esc)//N`, where `N` is some number greater than one and `v_(esc)` is escape speed on the earth. Neglecting the rotation of the earth and air resistance, the maximum altitude attained by the shell will be (`R_(E)` is radius of the earth):
View SolutionA planet of small mass `m` moves around the sun of mass `M` along an elliptrical orbit such that its minimum and maximum distance from sun are `r` and `R` respectively. Its period of revolution will be:
View SolutionA satellite revolving around the planet in a circular orbit is to be raised to a bigger circular orbit. The required energy can be supplied to the satellite for achieving the bigger orbit:
View SolutionA spherical uniform planet is rotating about its axis. The velocity of a point on its equator is `V`. Due to the rotation of planet about its axis the acceleration due to gravity `g` at equator is `1//2` of `g` at poles. The escape velocity of a particle on the planet in terms of `V`.
View SolutionThe escape speed from jupiter is approximately `59.5 kms^(-1)` and its radius is about `12` times that to earth. From this we may estimate the mean density of jupiter to be about (radius of earth =escape speed from the earth is `11.2 kgm^(-1)`
View SolutionAs observed from a place in Australia the pole star
View SolutionThe volume of mass and radius of sun are given by `M_(o)=2xx10^(30)kg` and `R_(o)=7xx10^(5)km` respectively. The pressure at the centre is bout `(g=6.67xx10^(-11)m^(3).kg^(-1) s^(-2))`
View SolutionAssume that the gas inside the sun behvaes very much like the perfect gas, the temperature at the centre of the sun is nearly (the number density of gas particles `(2rho)/(M_(H))`, Boltzmann constant `k_(B)=1.4xx10^(-23)J.K^(-1)` and mass of proton `M_(H)=1.67xx10^(-27) kg` )
View SolutionIn order to simulate different values of `g` aspiring astronauts are put on a plane which dives in a parabola given by the equation `x^2 = 500y`. Where `x` is horizontal, `y` is vertically upwards, both being measured in meter. The `x`-component of the velocity of the plane is constant throughout, and has the value of `360 km//h`. the effective `g`("g-force") experienced by an astronaut on the plane equals
View SolutionThe eccentricity of the earth's orbit is `0.0167`, the ratio of its maximum speed in its orbit to its minimum speed is
View SolutionThe time taken by the earth to travels over half its orbit, remote from the sun, separated by the minor axis is about `2` days more then half the year, then the eccentricity of the orbit is
View SolutionIf a spherically symmetric star of radius `R` collapsed under its own weight, neglecting any forces other than gravitational ones, what is the time required for collapse?
View SolutionFigure shows the kinetic energy `(E_(k))` and potential energy (`E_(p)`) curves for a two-particle system. Name the point(s) at which the system is a bound system.

View SolutionA tunnel is dug along a chord of the earth at a perpendicular distance `R//2` from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with `x` (distance of the particle from the centre) according to
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:

View SolutionA double star consists of two stars having masses `M` and `2M`. The distance between their centres is equal to `r`. They revolve under their mutual gravitational interaction. Then, which of the following statements are not correct?
View SolutionTwo satellites `S_(1)` and `S_(2)` are revolving around the earth in coplanar concentric orbits in the opposite sense. At `t=0`, the position of satellites are shown in the diagram. The periods of `S_(1)` and `S_(2)` are `4h` and `24h`, respectively. The radius of orbit of `S_(1)` is `1.28xx10^(4)km`. For this situation, mark the correct statement (s).

View SolutionA solid sphere of mass `m` and radius `r` is placed inside a hollow thin spherical shell of mass `M` and radius `R` as shown in the figure. A particle of mass `m'` is placed on the line joining the two centres at a distance `x` from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

`rltxlt2r`
View SolutionA solid sphere of mass `m` radius `r` is placed inside a hollow thin spherical shell of mass `M` and radius `2r` as shown in figure. A particle of mass `m'` is placed on the line joining the two centres at a distance `x` from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
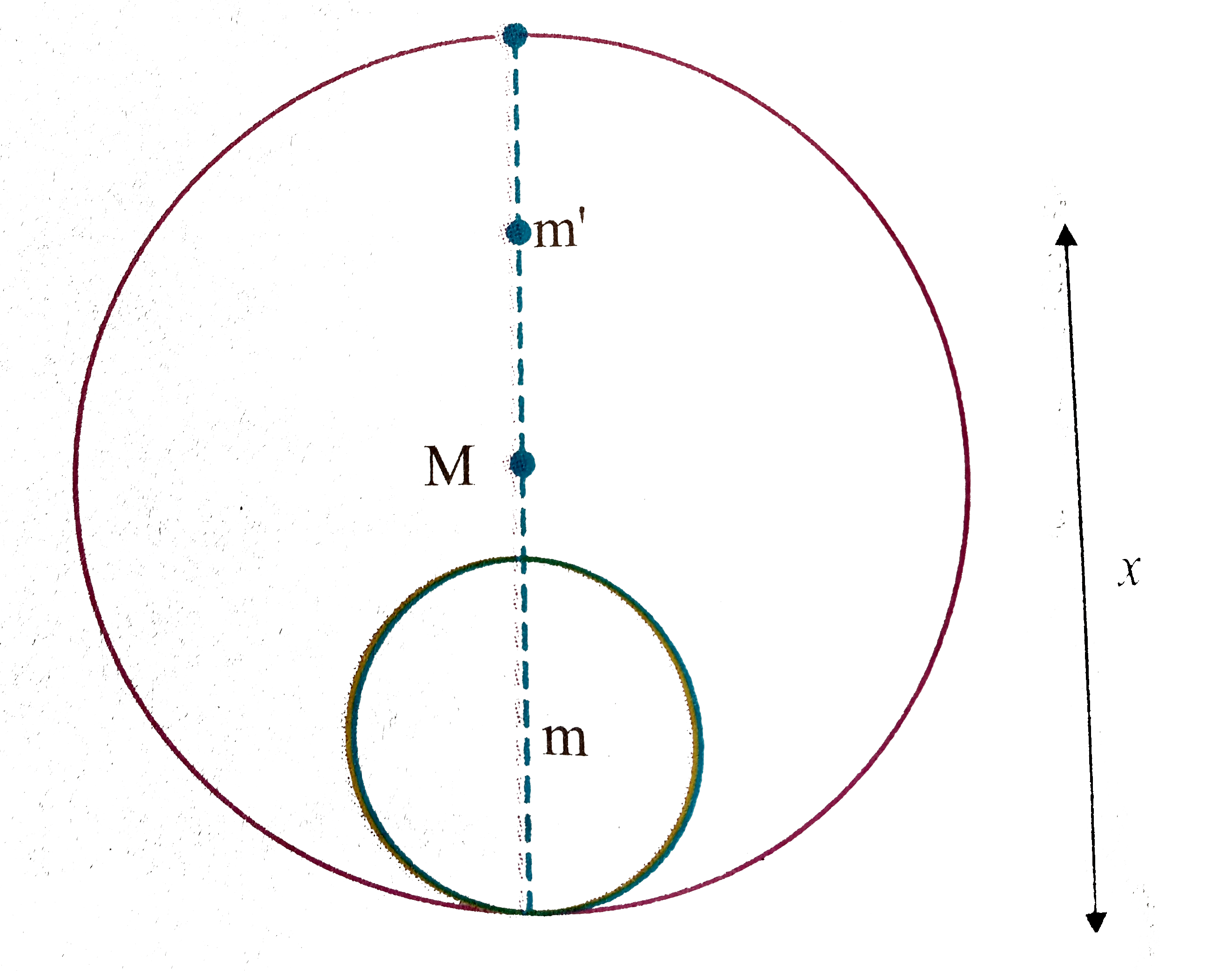
`2rltxlt2R`
View SolutionA solid sphere of mass `m` radius `r` is placed inside a hollow thin spherical shell of mass `M` and radius `2r` as shown in figure. A particle of mass `m'` is placed on the line joining the two centres at a distance `x` from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

`xgt2R`
View SolutionIn the graph shown, the `PE` of earth-satellite system is shown by a solid line as a function of distance `r` (the separation between earth's centre and satellite). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure by dotted lines.

Based on the above information, answer the following questions.
Mark the correct statement(s).
View SolutionIn the graph shown, the `PE` of earth-satellite system is shown by a solid line as a function of distance `r` (the separation between earth's centre and satellite). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure by dotted lines.

Based on the above information, answer the following questions.
If object having total energy `E_(1)` is having the same `PE` curve as shown in the figure, then
View SolutionIn the graph shown, the `PE` of earth-satellite system is shown by a solid line as a function of distance `r` (the separation between earth's centre and satellite). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure by dotted lines.

Based on the above information, answer the following questions. If both the objects have the same `PE` curve as shown in the figure, then
View Solution_S01_033_Q01.png)
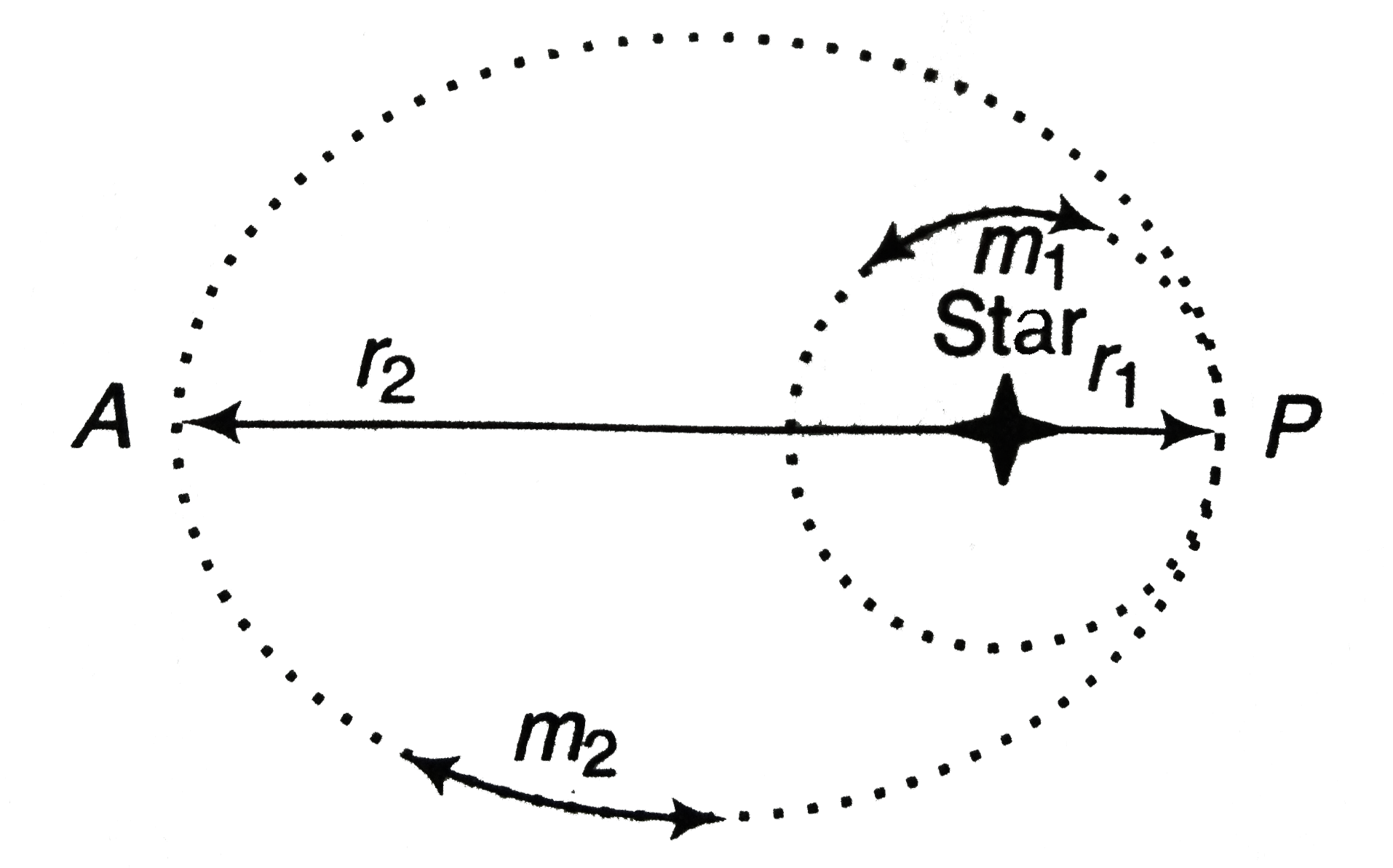
A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass `M=2xx10^(33)kg`. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is `r=10^(11)` m and the orbital period each star is `1.6xx10^(7)s` [take `pi^(2)=10` and `G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2)`]
Q. The mass m of the outer stars is:
View Solution_S01_034_Q01.png)
A triple stars system consists of two stars each of mass m in the same circular orbit about central star with mass `M=2xx10^(33)kg`. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is `r=10^(11)` m and the orbital period each star is `1.6xx10^(7)s` [take `pi^(2)=10` and `G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2)`]
Q. The orbital velocity of each star is
View Solution_S01_035_Q01.png)
A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass `M=2xx10^(33)kg`. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is `r=10^(11)` m and the orbital period each star is `1.6xx10^(7)s` [take `pi^(2)=10` and `G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2)`]
Q. The total mechanical energy of the system is
View SolutionConsider a hypothetical planet which is very long and cylinderical. The density of the planet is `rho`, its radius is `R`.

What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?
View SolutionConsider a hypothetical planet which is very long and cylinderical. The density of the planet is `rho`, its radius is `R`.

If an object is projected radially outwards from the surface such that it reaches upto a maximum distance of `3R` from the axis then what should be the speed of projection?
View SolutionConsider a hypothetical planet which is very long and cylinderical. The density of the planet is `rho`, its radius is `R`.
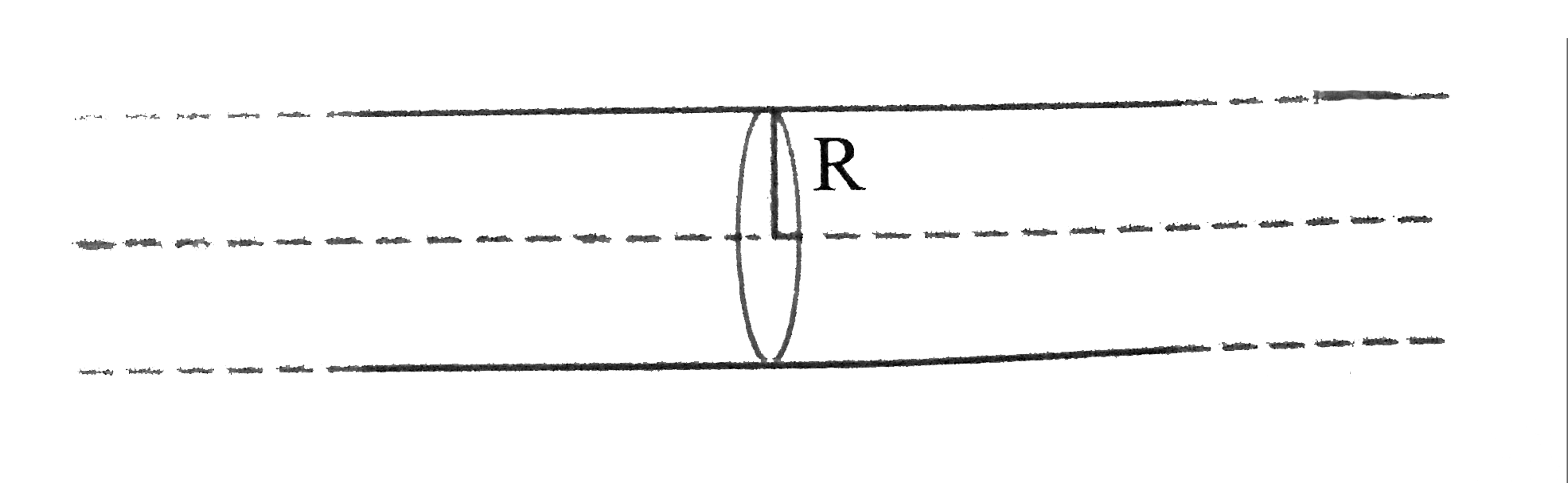
Assume that the planet is rotating abouts its axis with time period `T`. How far from the axis of the planet do the synchronous telecommunications satellite orbit?
View SolutionTwo planets of equal mass orbit a much massive star (figure). Planet `m_(1)` moves in circular orbit of radius `1 xx 10^(8) km` with period `2 yr`. Planet `m_(2)` moves in an elliptical orbit with closest distance `r_(1) = 1 xx 10^(8) km` and farthest distance `r_(2) = 1.8 xx 10^(8) km`, as shown.
(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of `m_(2)'s` orbit.
(b) Which planet has the greater speed at point `P`? Which has the greater total energy?
(c ) Compare the speed of planet `m_(2)` at `P` with that at `A`.
View SolutionTwo planets of equal mass orbit a much massive star (figure). Planet `m_(1)` moves in circular orbit of radius `1 xx 10^(8) km` with period `2 yr`. Planet `m_(2)` moves in an elliptical orbit with closest distance `r_(1) = 1 xx 10^(8) km` and farthest distance `r_(2) = 1.8 xx 10^(8) km`, as shown.

(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of `m_(2)'s` orbit.
(b) Which planet has the greater speed at point `P`? Which has the greater total energy?
(c ) Compare the speed of planet `m_(2)` at `P` with that at `A`.
View SolutionTwo planets of equal mass orbit a much massive star (figure). Planet `m_(1)` moves in circular orbit of radius `1 xx 10^(8) km` with period `2 yr`. Planet `m_(2)` moves in an elliptical orbit with closest distance `r_(1) = 1 xx 10^(8) km` and farthest distance `r_(2) = 1.8 xx 10^(8) km`, as shown.

(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of `m_(2)'s` orbit.
(b) Which planet has the greater speed at point `P`? Which has the greater total energy?
(c ) Compare the speed of planet `m_(2)` at `P` with that at `A`.
View SolutionA star can be considered as spherical ball of hot gas of radius `R`. Inside the star, the density of the gas is `rho_(r)` at radius `r` and mass of the gas within this region is `M_(r)`.
The correct differential equation for variation of mass with respect to radius is (refer to the adjacent figure)
View SolutionA star can be considered as spherical ball of hot gas of radius `R`. Inside the star, the density of the gas is `rho_(r)` at radius `r` and mass of the gas within this region is `M_(r)`.
A star in it's prime age is said to be under quilibrium due to gravitational pull and outward radiation pressure `(p)`. consider the shell of thikness `dr` as in the figure of previous question. if the pressure on this shell is `dp` then the correc equation is (`G` is universal gravitational constant)
View SolutionA planet revolves about the sun in an elliptical orbit of semi-major axis `2xx10^(12) m`. The areal velocity of the planet when it is nearest to the sun is `4.4xx10^(16) m//s`. The least distance between the planet and the sun is `1.8xx10^(12) m//s`. The minimum speed of the planet in `km//s` is `10 K`. determine the value of `K`.
View SolutionThe gravitational potential energy of satellite revolving around the earth in circular orbit is `4MJ`. Find the additional energy (in `MJ`) that should be given to the satellite so that it escape from the gravitational field of the earth.
View SolutionA particle is projected from the surface of earth with intial speed of 4 km/s. Find the maximum height attained by the particle. Radius of earth = 6400 km and `g = 9.8 m//s^(2)`
View SolutionEarth is a sphere of uniform mass density. If the weight of the body is `10 n N` half way down. The body weighed `100 N` on the surface. An infinite collection of equal masses of `2kg` each are kept on a horizontal line (`X`-axis) at positions `x=1m,2m,4m,8m`...... find the gravitational potential at `x=0` in `GJ` unit.
View SolutionThree uniform spheres, each having a mass `M=5kg` and radius `a=2.5m` are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in `GN` on any of the spheres due to the other two.
View SolutionThree uniform spheres, each having a mass `M=5kg` and radius `a=2.5m` are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in `GN` on any of the spheres due to the other two.
View SolutionA cord of length `64 m` is used to connected a `100 kg` astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is `6400 km`.
View SolutionTwo satellites of mass ratio `1:2` are revolving around the earth in circular orbits such that the distance of the second satellite is four times as compared to the distance of the first satellite. Find the ratio of the centripetal forces.
View Solution
LEVEL-V questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example