Complete Solutions to EXERCISE -IV of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | EXERCISE -IV |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
The earth is an approximate sphere. If the interior contained matter which is not of the same density every where, then on the surface of the earth, the acceleration due to gravity
View SolutionDifferent points in the earth are at slightly different distance from the sun and hence experience different force due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the `CM` (centre of mass) causing translation and a net torque at the `CM` causing rotation around an axis through the `CM`. for the earth-sun system (approximating the earth as a uniform density sphere).
View SolutionSatellites orbiting the earth have finite life and sometimes debris of satellites fall to the earth. This is because,
View SolutionParticles of masses 2M, m and M are respectively at points A, B and C with AB=1/2(CB). M is much -much smaller than M and at time t =0, they are at rest as given in figure.
At subsequent times before any collision takes place

View SolutionA point mass is orbiting a significant mass M lying at the focus of the elliptical orbit having major and minor axes given by 2 a and 2b respectively. Let r be the distance between the mas M and the end point of major or axis. Velocity of the particle can be given as
View SolutionA planet of mass `m` revolves in elliptical orbit around the sun of mass `M` so that its maximum and minimum distance from the sun equal to `r_(a)` and `r_(p)` respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the end of the minor axis and close to the sun is
View SolutionThe gravitational field in a region is given by `vecE = (3hati- 4hatj) N kg^(-1)`. Find out the work done (in joule) in displacing a particle by `1 m` along the line `4y = 3x + 9`.
View SolutionA solid sphere of uniform density and mas M has radius 4M. Its centre is at the origin of the coordinate system. Two speres of radii 1 m are taken out so tht their centres are at `P(0,-2,0)` and `Q(0,2,0)` respectively. This leaves two sphericla cavities. What is the gravitational field at the origin of the coordinate axes?

View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `R`, at a distance `2R` from its centre `O`. A small particle starts from `P` and reaches `O` under gravitational attraction only. Its speed at `O` will be
View SolutionTwo having masses M and 2M, respectively, having the same radius R are placed coaxially as shown in the figure. If the mass distribution on both the rings is non uniform, then the gravitational potential at point P is

View SolutionA point of mass m is released from rest at a distance of 3R from the cente of a then walled hollow spehre of radius R and mass M as shown. The hollow sphere is fixed in position and the motion is due to only gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. Then the velocity of point mas when it passes through point P at distance R/2 from the centre of the sphere is

View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
View SolutionFrom a solid sphere of mass m and radius R, a spherical portion of raidus R/2 is removed, as shown in the figure. Taking gravtitational potential V=0 at `r=0`, the potential at the centre of the cavity thus formed is (G=Gravitational constant).

View SolutionThe density of the core of a planet is `rho_(1)` and that of the outer shell is `rho_(2)`. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. The ratio of denisty `rho_(1)//rho_(2)` will be

View SolutionTwo concnetric shells of different masses `m_(1)` and `m_(2)` are having a sliding particle of mass m. The forces on the particle at position I, II and II are

View SolutionSuppose a vertical tunnel is dug along the diameter of earth assumed to be a sphere of uniform mass having density `rho`. If a body of mass m is a dropped in this tunnel, its acceleration at a distance y from the centre is given by

View SolutionThe centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance `sqrt(8)` R apart as shwon in fig. The force of attraction between the ring and the sphere is

View SolutionA mass `m` extends a vertical helical spring of spring constant `k` by `xm` at the surface of the earth. Extension in spring by the same mass at height `h` meter above the surface of the earth is
View SolutionA spherical shell is cut into two pieces along a chord as shown in the figure. P is point on the plane of the chord. The gravitational field at P due to the upper part is `I_(1)` and that due to the lower part is `I_(2)`.What is the relation between them?

View SolutionThe magnitudes of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `E_(1)` and `E_(2)` respectively. Then:
View SolutionGravitational field intensity at the centre of the semi circle formed by a thin wire AB of mass m and length L is

View SolutionTwo equal masses each `m` are hung from a balance whose scale pans differ in vertical height by `h`. The error in weighing is
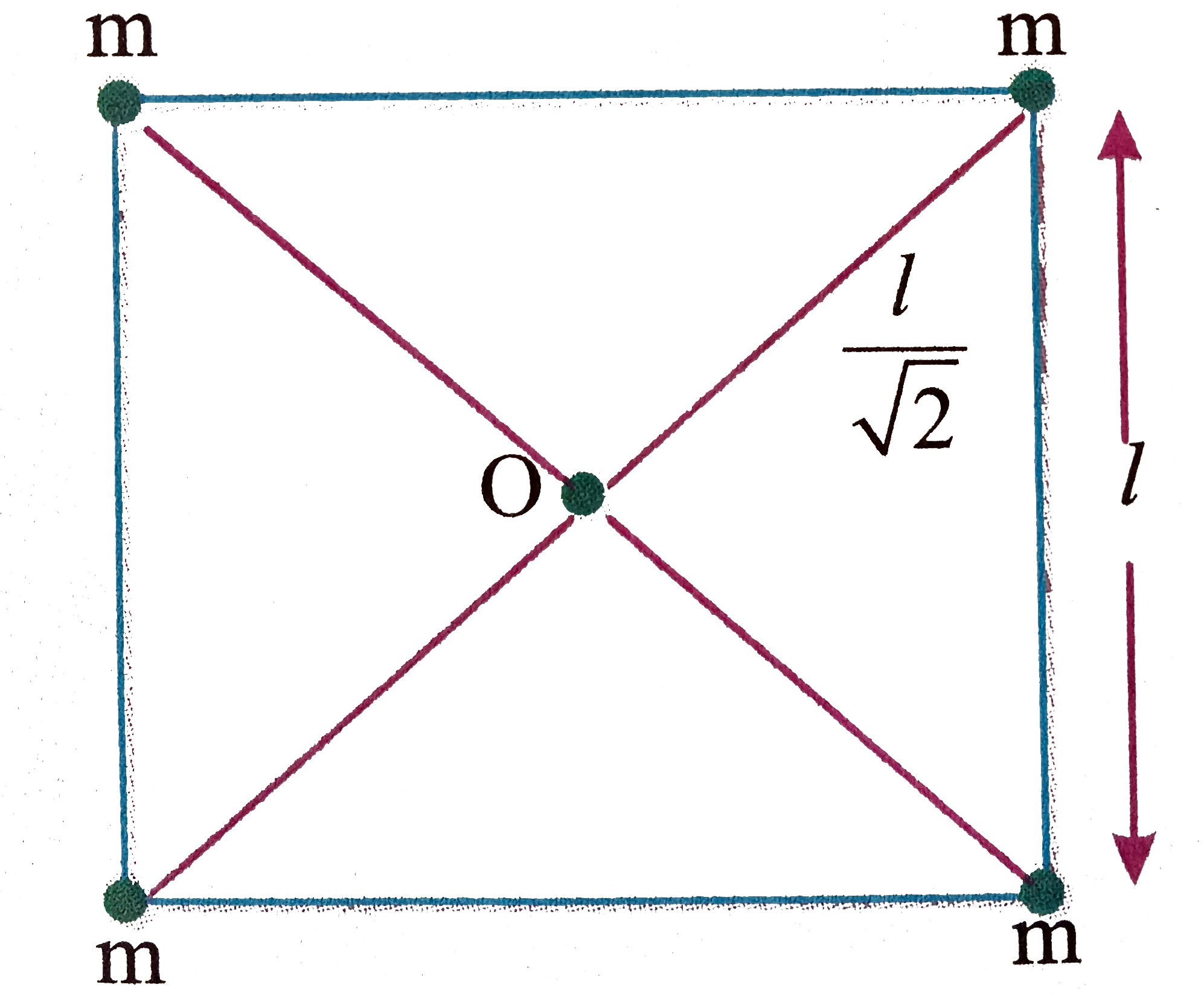
View SolutionFind the gravitational potential energy of a system of four particles, each of mass `m` placed at the verticles of a square of side `l`. Also obtain the gravitaitonal potential at centre of the square.
View SolutionA thin uniform annula disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass from point P on its axis on infinity is

View SolutionThe gravitational force in a region is given by, `vec(F)=mayhati+maxhatj` The work done by gravitational force to shift a point mass `m` from `(0,0,0)` is `(x_(0),y_(0),z_(0))` is
View SolutionThe gravitational field in a region due to a certain mass distribution is given by `vec(E)=(4hati-3hatj)N//kg`. The work done by the field in moving a particle of mass `2kg` from `(2m,1m)` to `(2/3m,2m)` along the line `3x+4y=10` is
View SolutionA particle of mass `1kg` is placed at a distance of `4m` from the centre and on the axis of a uniform ring mass `5kg` and radius `3m`. The work done to increase the distance of the particle from `4m` to `3sqrt(3)`m is
View SolutionConsider two configuration in fig (i) and fig (ii)

The work done by external agent in changing the configuration from fig (i) to fig (ii) is
View SolutionTwo concentric sphereical shells A and B of radii R and 2R and masses 4 M and M respectively are as shown. The gravitational potential at pont p at distance `r(Rltrlt2R)` from centre of shell is `(r=1.5R)`

View SolutionA particle is placed in a field characterized by a value of gravitational potential given by `V=-kxy`, where `k` is a constant. If `vec(E)_(g)` is the gravitational field then
View SolutionIn a certain region of space, the gravitational field is given by `-(k)/(r)` where `r` is the distance and k is a constant. If the gravitaional potential at `r=r_(0)` be `V_(0)`, then what is the expression for the gravitaional potential (V)-
View SolutionGraviational acceleration on the surface of plane fo `(sqrt6)/(11)g.` where g is the gracitational acceleration on the surface of the earth. The average mass density of the planet is `(2)/(3)` times that of the earth. If the escape speed on the surface of the earht is taken to be `11 kms^(-1)` the escape speed on teh surface of the planet in `kms^(-1)` will be
View SolutionA spherically symmetric gravitational system of particles has a mass density` rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):}` where`rho_0` is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce `r(0ltrltOO)` form the centre of the system is represented by
View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
View SolutionIf earth were to rotate on its own axis such that the weight of a person at the equator becomes half the weight at the poles, then its time period of rotation is (g = acceleration due to gravity near the poles and R is the radius of earth) (Ignore equatorial bulge)
View SolutionTwo identical thin ring each of radius `R` are co-axially placed at a distance `R`. If the ring have a uniform mass distribution and each has mass `m_(1)` and `m_(2)` respectively, then the work done in moving a mass `m` from the centre of one ring to that of the other is :
View SolutionTwo bodies of masses m and M are placed at distance d apart. The gravitational potential (V) at the position where the gravitational field due to them is zero V is
View SolutionAn asteroids as moving towards a planet of mass M and radius R,from a large distance with intial speed `v_(0)` and impact parameter d as shown in the figure. The minimum value of `v_(0)` such that the asteriod does not his the planet is

View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, `h lt lt R`). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth's gravitational field, is close to :(Neglect the effect of atmosphere.)
View Solution
EXERCISE -IV questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example