Complete Solutions to Solved Example of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| NARAYANA | Solved Example |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
An artificial satellite is in an elliptical orbit around the earth with aphelion of `6R` and perihelion of `2R` where `R` is radius of the earth `=6400km`. Calculate the eccentricity of the elliptical orbit.
View SolutionThe mean distance of a planet from the sun is approximately `1//4` times that of the earth from the the sun. Find the number of years required for the planet to make one revolution about the sun.
View SolutionLet the speed of the planet at the perihelion `P` in figure be `v_(P)` and the Sun planet distance `SP` be `r_(P)`. Relater `r_(P), v_(P)` to the corresponding quantities at the aphelion `(r_(A),v_(A))`. Will the planet take equal times to transverse `BAC` and `CPB`?

View SolutionLet us consider that our galaxy consists of `2.5xx10^(11)` stars each of one solar mass. How long will this star at a distance of `50,000` light year from the galastic entre take to complete one revolution? Take the diameter of the Milky way to be `10^5ly. G=6.67xx 10^(-11) Nm^(2) Kg^(-2). (1 ly= 9.46xx10^(15)m)`
View SolutionIf two particles each of mass `m` are placed at the two vertices of an equilateral triangle of side `a`, then the resultant gravitational force on mass `m` placed at the third vertex is
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionIf four different masses `m_1, m_2,m_3` and `m_4` are placed at the four corners of a square of side `a`, the resultant gravitational force on a mass `m` kept at the centre is
View SolutionA thin rod of mass `M` and length `L` is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass `m` at the centre of curvature?
View SolutionFor particles of equal masses M that move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionMass `M` is split into two parts `m` and `(M-m)`, which are then separated by a certain distance. What is the ratio of `(m//M)` which maximises the gravitational force between the parts ?
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to `R^(-5//2)`, then
(a) `T^(2)` is proportional to `R^(2)`
(b) `T^(2)` is proportional to `R^(7//2)`
(c) `T^(2)` is proportional to `R^(3//3)`
(d) `T^(2)` is proportional to `R^(3.75)`.
View SolutionThree sperical balls of masses `1kg, 2kg` and `3kg` are placed at the corners of an equilateral triangle of side `1m.` Find the magnitude of the gravitational force exerted by `2kg` and `3kg` masses on `1kg` mass.
View SolutionTwo particles of masses `1kg` and `2kg` are placed at a distance of `50cm`. Find the initial acceleration of the first particle due to gravitational force.
View SolutionAn infinite number of particles each of mass `m` are placed on the positive X-axis of `1m, 2m, 4m, 8m,...` from the origin. Find the magnitude of the resultant gravitational force on mass `m` kept at the origin.
View SolutionIn a double star system, two stars of masses `m_1` and `m_2` separated by a distance `x` rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View SolutionIn Cavendish's experiment, let each small mass be `20g` and each large mass be `5kg`. The rod connecting the small masses is `50cm` long, while the small and the large spheres are separated by `10.0cm.` The torsion constant is `4.8xx10^(-8) kg m^2 s^(-2)` and the resulting angular deflection is `0.4^@`. Calculate the value of universal gravitational constant `G` from this data.
View SolutionThe mean orbital radius of the Earth around the Sun is `1.5 xx 10^8 km`. Estimate the mass of the Sun.
View SolutionA particle of mass `m` is situated at a distance `d` from one end of a rod of mass `M` and length `L` as shown in diagram. Find the magnitude of the gravitational force between them

View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius `R`, at a distance of `3R` from the centre of the sphere is `F_1.` A spherical hole of radius `(R//2)` is now made in the sphere as shown in diagram. The sphere with hole now exerts a force `F_2` on the same particle. ratio of `F_1` to `F_2` is
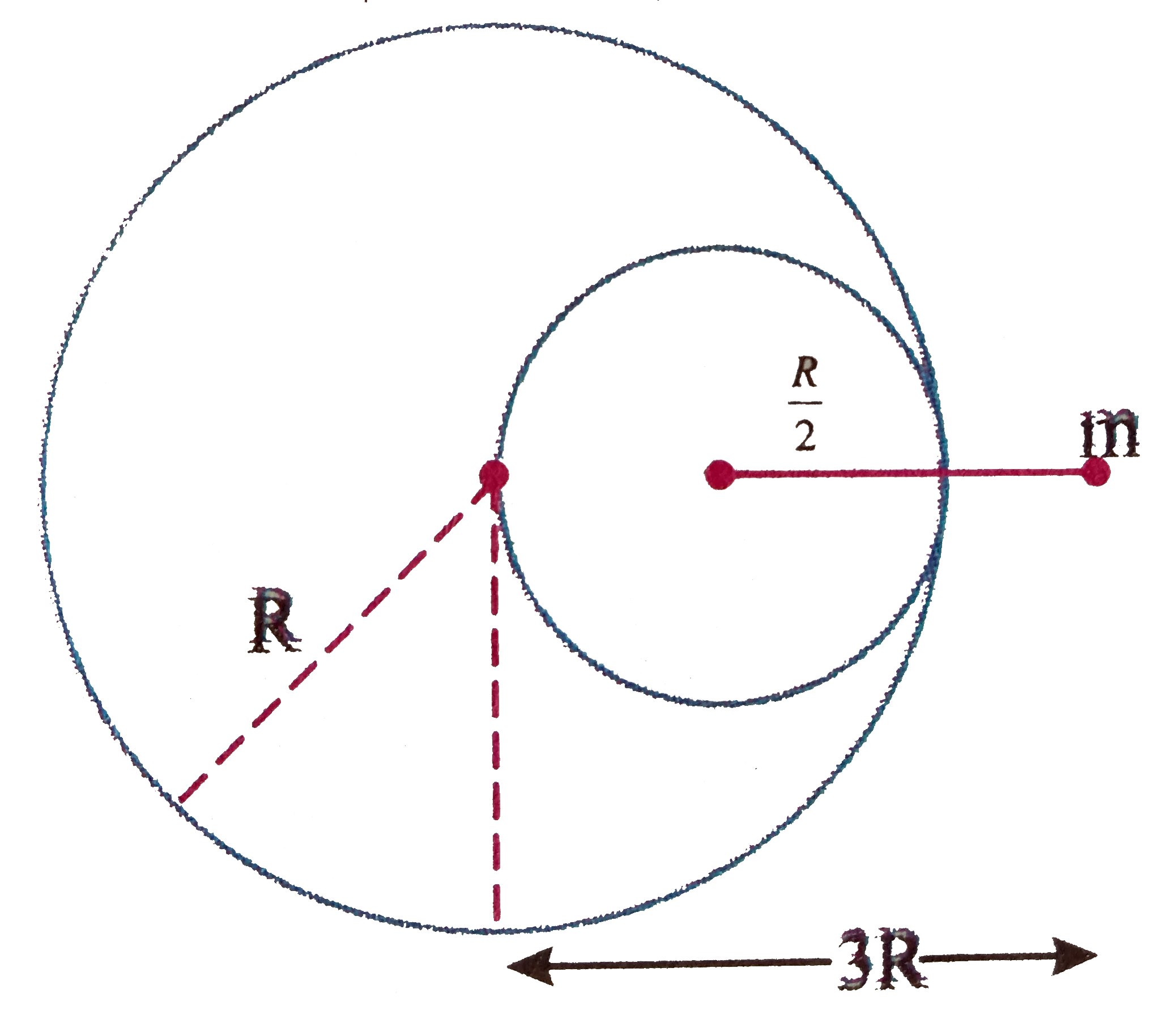
View SolutionA star `2.5` times the mass of the sun is reduced to a size of `12km` and rotates with a speed of `1.5rps.` Will an object placed on its equator remain stuck to its surface due to gravity? (Mass of the sun `=2xx10^(30) kg`)
View SolutionWhat is the time period of rotation of the earth around its axis so that the objects at the equator becomes weightless? (`g=9.8 m//s^2`, radius of the earth `=6400km`)
View SolutionThe height at which the acceleration due to gravity becomes `(g)/(9)` (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionHow much above the surface of the earth does the acceleration due to gravity reduce by `36%` of its value on the surface of the earth.
View SolutionFind the percentage decrease in the weight of the body when taken to a depth of `32 km` below the surface of earth. Radius of the earth is `6400 km`.
View SolutionA man can jump `1.5m` on the Earth. Calculate the approximate height he might be able to jump on a planet whose density is one-quarter that of the Earth and whose radius is one-third that of the Earth.
View SolutionTwo bodies of masses `100kg` and `10,000kg` are at a distance of `1m` apart. At what distance from `100kg` on the line joining them will the resultant gravitational field intensity be zero?
View SolutionThe gravitational field due to a mass distribution is given by `E=-K//x^3` in x-direction. Taking the gravitational potential to be zero at infinity, find its value at a distance `x`.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
View SolutionThe gravitational field in a region is given by `vecE=-(20Nkg^(-1))(hati+hatj)`. Find the gravitational potential at the origin `(0,0)` in `J kg^(-1)`
View SolutionCalculate the gravitational potential at the centre of base of a solid hemisphere of mass `M`, radius `R`.
View SolutionThe gravitational field in a region is given by the equation `E=(5i + 12j) N//kg`. If a particle of mass `2kg` is moved from the origin to the point `(12m, 5m)` in this region, the change in the gravitational potential energy is
View SolutionFind the gravitational potential energy of a system of four particles, each of mass `m` placed at the verticles of a square of side `l`. Also obtain the gravitaitonal potential at centre of the square.
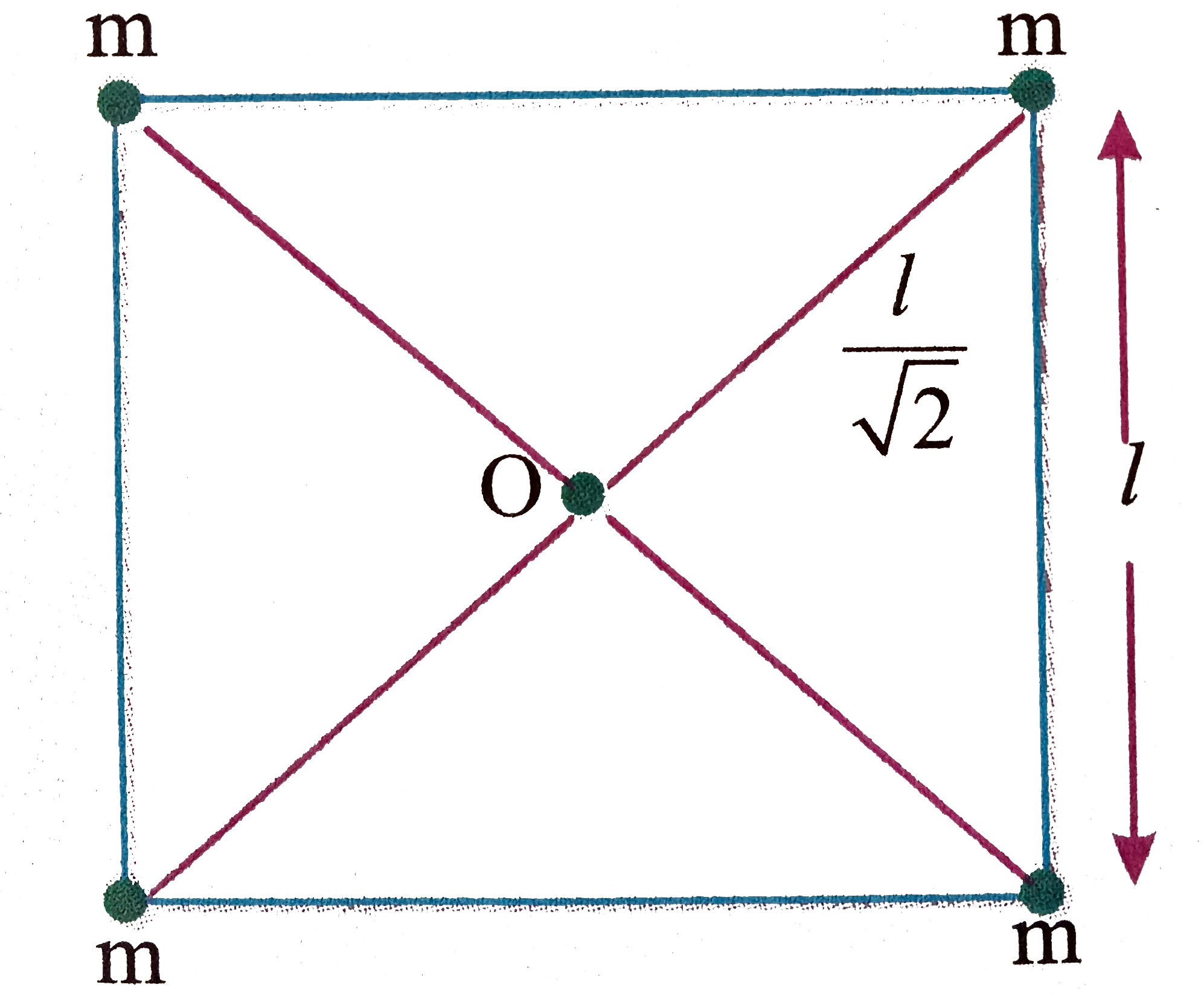
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
View SolutionIf Earth has mass nine times and radius twice that of the planet Mars, calculate the velocity required by a rocket to pull out of the gravitational force of Mars. Take escape speed on surface of Earth to be `11.2km//s`
View SolutionA rocket is fired with a speed, `v=2sqrt(gR)`, near the earth's surface and directed upwards. (a) Show that it will escape from the earth. (b) Show that in interstellar space its speed is `v=sqrt(2gR)`.
View SolutionA planet in a distant solar systyem is 10 times more massive than the earth and its radius is 10 times smaller. Given that the escape velocity from the earth is `11kms^(-1)`, the escape velocity from the surface of the planet would be
View SolutionA satellite orbits the earth at a height of `400km` above the surface. How much energy must be expanded to rocket the satellite out of the gravitational influence of earth? Mass of the satellite is `200kg,` mass of earth `=6.0 xx 10^(24) kg,` radius of earth `=6.4 xx 10^6 m`, `G=6.67xx10^(-11)Nm^2 kg^(-2).`
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If `R` is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA particle is fired vertically upward fom earth's surface and it goes up to a maximum height of 6400 km. find the initial speed of particle.
View SolutionIf a satellite is revolving around a planet of mass `M` in an elliptical orbit of semi-major axis `a`. Show that the orbital speed of the satellite when it is a distance `r` from the focus will be given by
`upsilon^(2) = GM[(2)/(r ) - (1)/(a)]`
View SolutionA rocket is fired vertically from the surface of Mars with a speed of `2kms^(-1)`. If `20%` of its initial energy is lost due to Martian atmospheric resistance, how far will the rocket go from the surface of Mars before returning to it? Mass of Mars `=6.4xx10^(23)kg`, radius of Mars `=3395 km`,
View SolutionTwo heavy spheres each of mass `100kg` and radius `0.1m` are placed `1m` apart on a horizontal table. What is the gravitationl field and potential at the mid point of the line joining their centres. The gravitational potential difference between the surface of a planet and a point `20m` above it is `16J//kg`. Calculate the workdone in moving a `2kg` mass by `8m` on a slope of `60^@` from the horizontal.
View SolutionThe gravitational potential difference between the surface of a planet and a point `20 m` above it is `16 J//kg`. Calculate the work done in moving a `4 kg` body by `8m` on a slope of `60^@` from the horizontal.
View SolutionThe mass of a spaceship is 1000kg. It is to be launched from the earth's surface out into free space. The value of g and R (radius of earth) are `10m/s^2` and 6400 km respectively. The required energy for this work will be:
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionTwo uniform soild spheres of equal radii `R` but mass `M` and `4M` have a centre to centre separation `6 R`, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass` m` is projected from the surface of the sphere of mass `M` directly towards the centre of teh second. Obtain an expression for the minimum speed `upsilon` of the projectile so that it reaches the surface of second sphere.
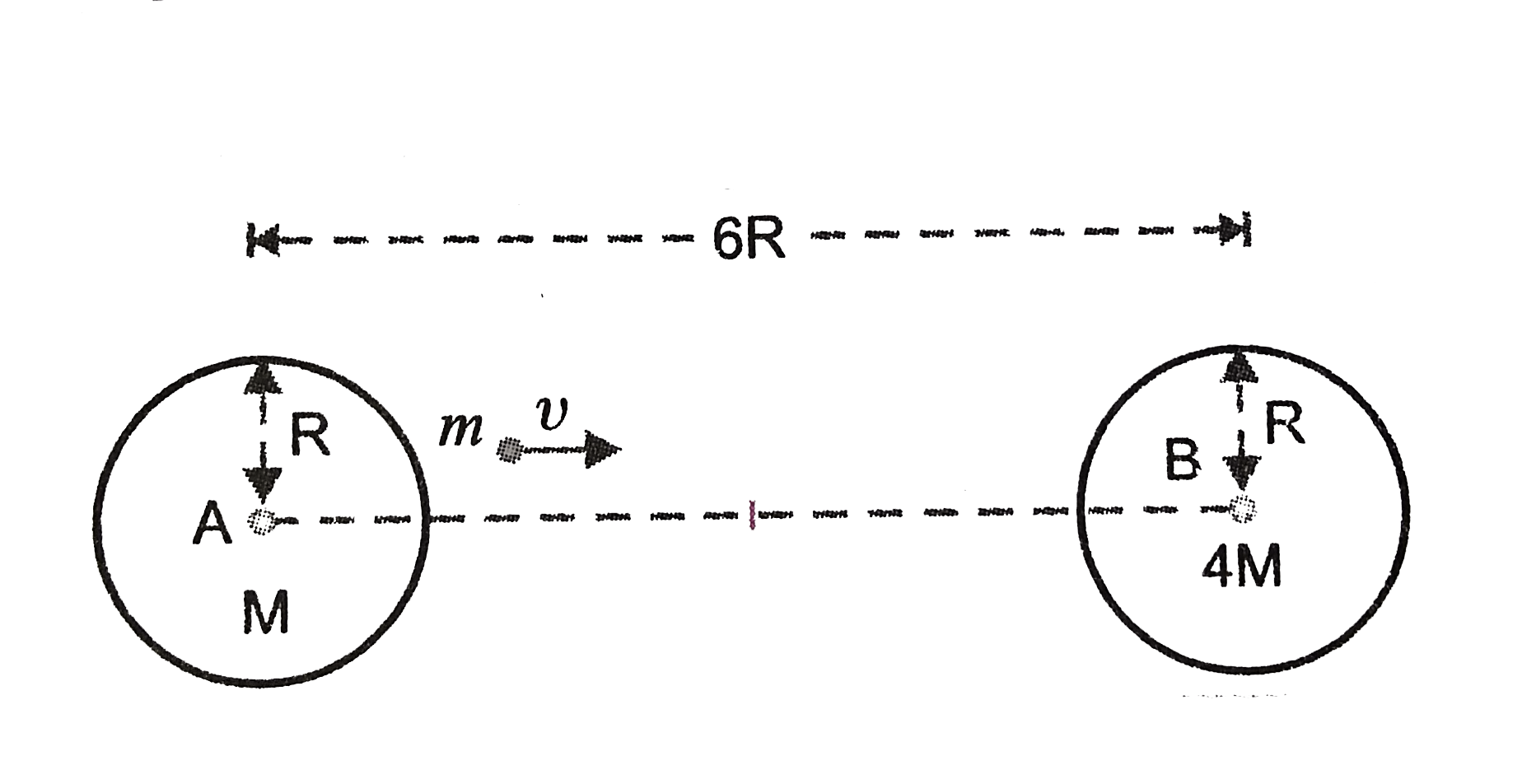
View SolutionA `400 kg` satellite is in a circular orbit of radius `2 R_(E)` around the Earth. How much energy is required to transfer it to a circular orbit of radius `4 R_(E)`? What are the changes in the kinetic and potential energies?
Given `g = 9.81 m^(-2) , R_(E) = 6.37 xx 10^(6) m`.
View SolutionA satellite of mass `m` is orbiting the earth in a circular orbit of radius `r`. It starts losing energy due to small air resistance at the rate of `C J//s`. Then the time teken for the satellite to reach the earth is...........
View SolutionTwo satellites of same mass are launched in the same orbit round the earth so as to rotate opposite to each other. They soon collide inelastically and stick together as wreckage. Obtain the total energy of the system before and just after the collision. Describe the subsequent motion of the wreckage.
View SolutionA lauching vehicle carrying an artificial satellite of mass `m` is set for launch on the surface of the earth of mass `M` and radius `R`. If the satellite intended to move in a circular orbit of radius `7R`, the minimum energy required to be spent by the launching vehicle on the satellite is
View Solution
Solved Example questions and complete solutions for chapter GRAVITATION of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS GRAVITATION
- C.U.Q
- EVALUATE YOURSELF -3
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF-4
- EVALUATE YOURSELF-5
- EXERCISE -I (C.W.)
- EXERCISE -I (H.W.)
- EXERCISE -II (C.W.)
- EXERCISE -II (H.W.)
- EXERCISE -III
- EXERCISE -IV
- ILLUSTRATION
- LEVEL -I(H.W)
- LEVEL I(C.W.)
- LEVEL II (C.W.)
- LEVEL III
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- NCERT BASED QUESTIONS
- Solved Example