Complete Solutions to JEE Main And Advanced of chapter LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF MOTION |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is `5m//s^2`, the frictional force acting on the block is…………newtons.
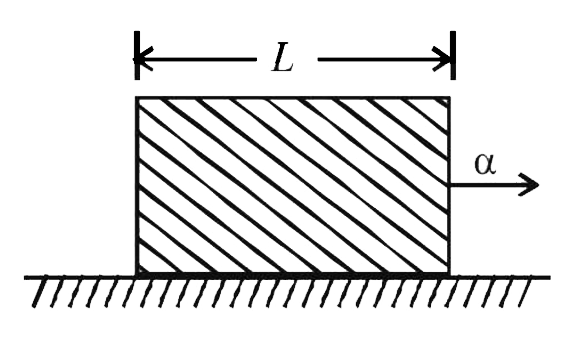
View SolutionA uniform rod of length L and density `rho` is being pulled along a smooth floor with a horizontal acceleration `alpha` (see Fig.) The magnitude of the stress at the transverse cross-section through the mid-point of the rod is……..
View SolutionA rocket moves forward by pushing the surrounding air backwards.
View SolutionWhen a person walks on a rough surface, the frictional force exerted by the surface on the person is opposite to the direction of his motion.
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of `40^@`. When its angular displacement is `20^@`, the tension in the string is greater than `mg cos 20^@`
View SolutionThe pulley arrangements of Figs. (a) and (b) are identical. The mass of the rope is negligible. In (a) the mass m is lifted up by attaching a mass 2m to the other end of the rope. In (b), m is lifted up by pulling the other end of the rope with a constant downward force `F=2mg`. The acceleration of m is the same in both cases

View SolutionA ship of mass `3xx10^7kg` initially at rest, is pulled by a force of `5xx10^5N` through a distance of 3m. Assuming that the resistance due to water is negligible, the speed of the ship is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of `30^@` with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is `1//3`. If the line joining the center of the hemispherical surface to the insect makes an angle `alpha` with the vertical, the maximum possible value of `alpha` is given by

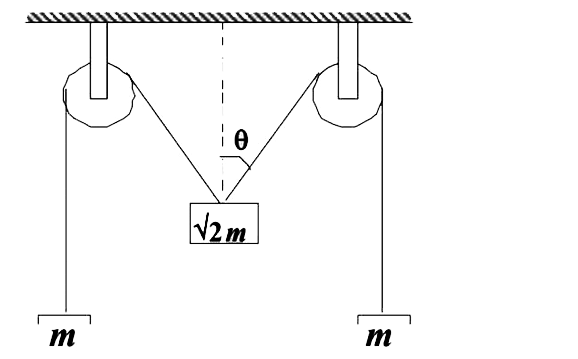
View SolutionThe pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle `theta` should be
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

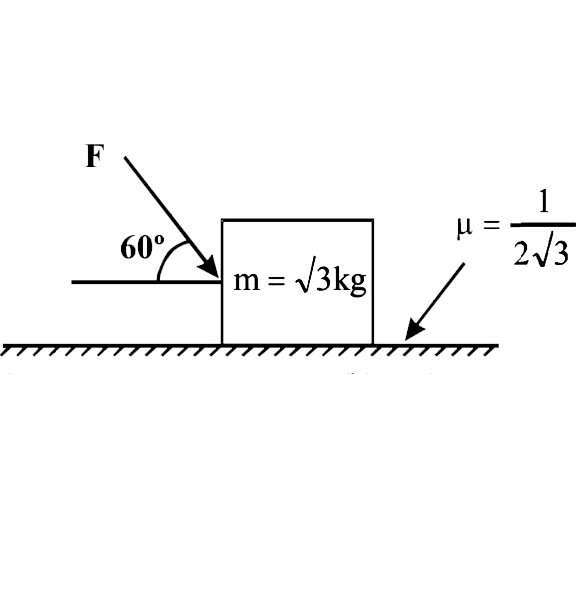
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View SolutionThe string between blocks of mass m and 2m is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass 2m and m (immediately after cutting)

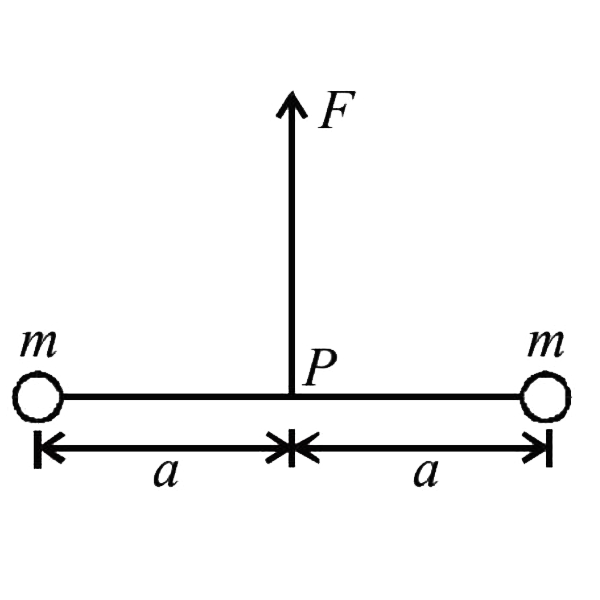
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance `a` from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View SolutionA particle moves in the X-Y plane under the influence of a force such that its linear momentum is `oversetrarrp(t)=A[haticos(kt)-hatjsin(kt)]`, where A and k are constants. The angle between the force and the momentum is
View SolutionA block of base `10 cm xx 10 cm` and height `15 cm` is kept on an inclined plane. The corfficient of friction between them is `sqrt(3)`. The inclination `theta` of this inclined plane from the horizontal plane is gradually increased frm `0^@`. Then
View SolutionA block of mass m is on an inclined plane of angle `theta`. The coefficient of friction between the block and the plane is `mu` and `tanthetagtmu`. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from `P_1=mg(sintheta-mucostheta)` to `P_2=mg(sintheta+mucostheta)`, the frictional force f versus P graph will look like
View SolutionA ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
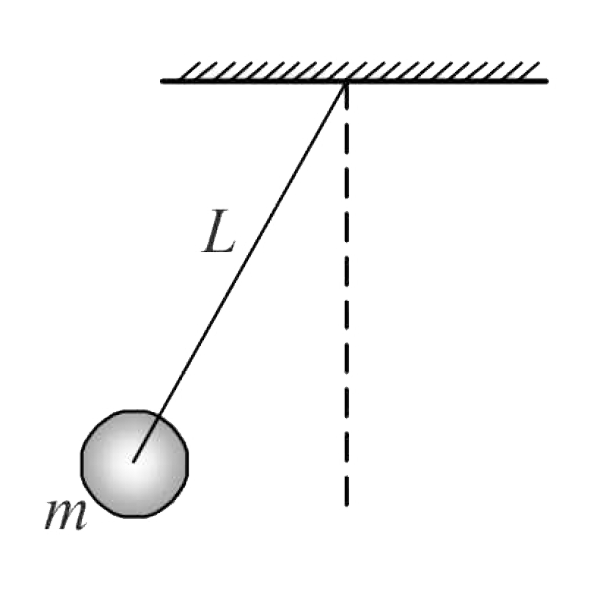
View SolutionThe image of an object, formed by a plano-convex lens at a distance of 8 m behind the lens, is real is one-third the size of the object. The wavelength of light inside the lens is 2/3 times the wavelength in free space. The radius of the curved surface of the lens is
View SolutionIn the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
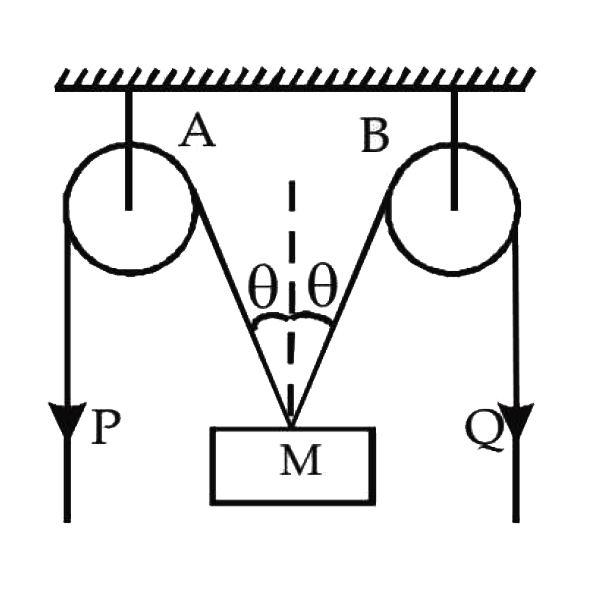
View SolutionA reference frame attached to the earth
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit `-phi` and `+phi`. For an angular displacement `theta(|theta|ltphi)`, the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
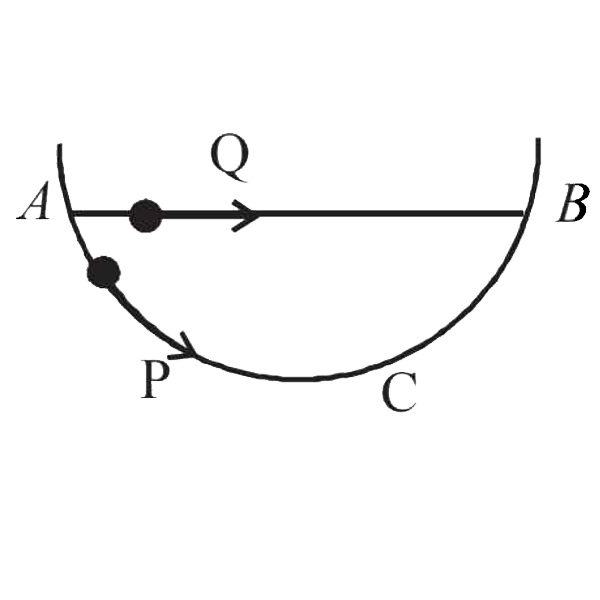
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at `t=0`. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at `t=0` along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let `t_P` and `t_Q` be the respective times taken by P and Q to reach the point B. Then:
View SolutionA small block of mass of 0.1 kg lies on a fixed inclined plane PQ which makes an angle `theta` with the horizontal. A horizontal force of 1N acts on the block through its centre of mass as shown in figure.
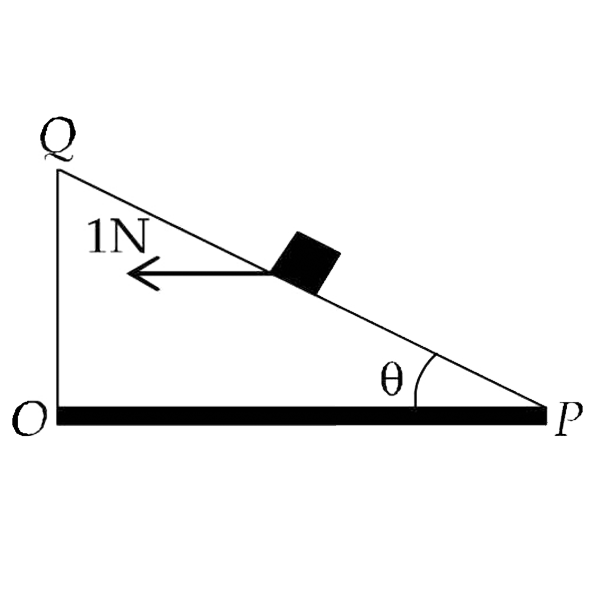
The block remains stationary if (take `g=10m//s^2`)
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
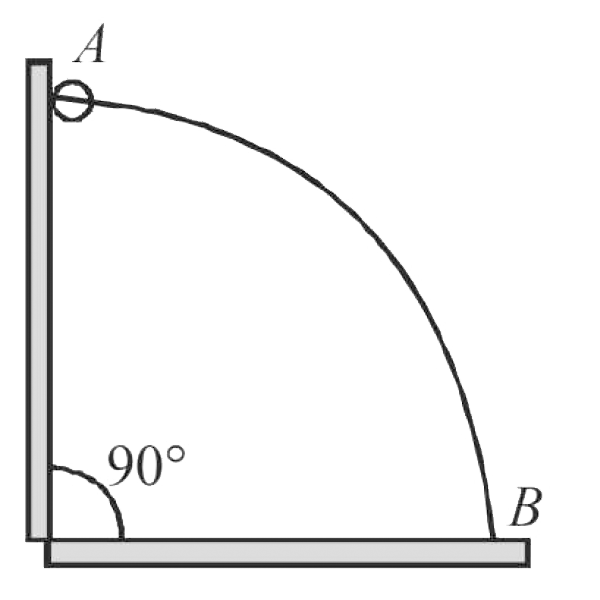
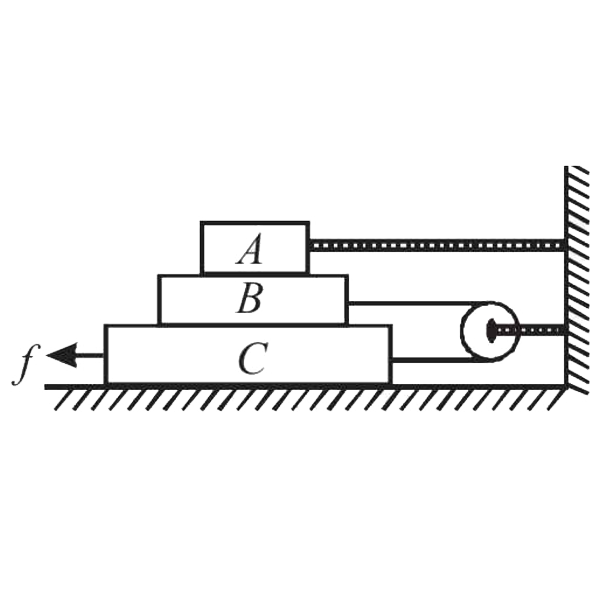
View SolutionIn the diagram shown, the blocks A, B and C weight, 3kg, 4kg and 5kg respectively. The coefficient of sliding friction between any two surface is 0.25. A is held at rest by a massless rigid rod fixed to the wall while B and C are connected by a light flexible cord passing around a frictionless pulley. Find the force F necessary to drag C along the horizontal surface to the left at constant speed. Assume that the arrangement shown in the diagram, B on C and A on B, is maintained all through. `(g=9.8m//s^2)`
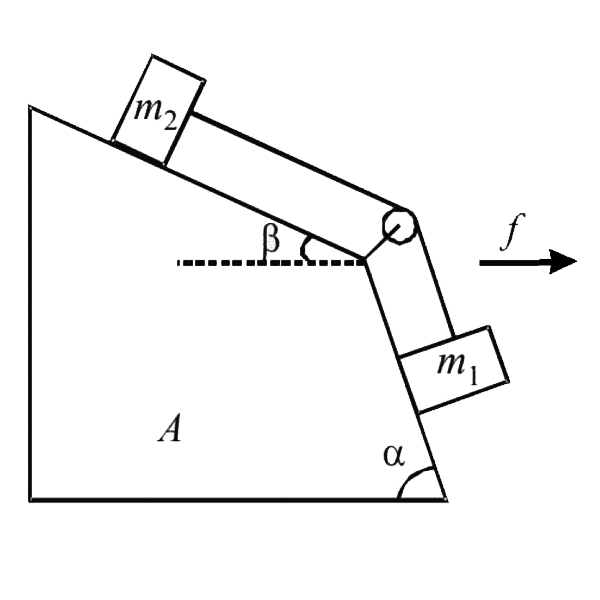
View SolutionTwo cubes of masses `m_1` and `m_2` be on two frictionless slopes of block A which rests on a horizontal table. The cubes are connected by a string which passes over a pulley as shown in figure. To what horizontal acceleration f should the whole system (that is blocks and cubes) be subjected so that the cubes do not slide down the planes. What is the tension of the string in this situation?
View SolutionA uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ]
View SolutionMasses `M_1`, `M_2` and `M_3` are connected by strings of negligible mass which pass over massless and friction less pulleys `P_1` and `P_2` as shown in fig The masses move such that the portion of the string between `P_1` and `P_2` in parallel to the inclined plane and the portion of the string between `P_2` and `M_3` is horizontal. The masses `M_2` and `M_3` are 4.0kg each and the coefficient of kinetic friction between the masses and the surfaces is 0.25. The inclined plane makes an angle of `37^@` with the horizontal.

If the mass `M_1` moves downwards with a uniform velocity, find
(i) the mass of `M_1`
(ii) The tension in the horizontal portion of the string `(g=9.8 m//sec^2, sin 37^@=3//5)`
View SolutionA particle of mass m rests on a horizontal floor with which it has a coefficient of static friction `mu`. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.
View SolutionTwo blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of `0.2kg//m`. The whole system of blocks wires and support have an upward acceleration of `0.2m//s^2`. Acceleration due to gravity is `9.8m//s^2`.
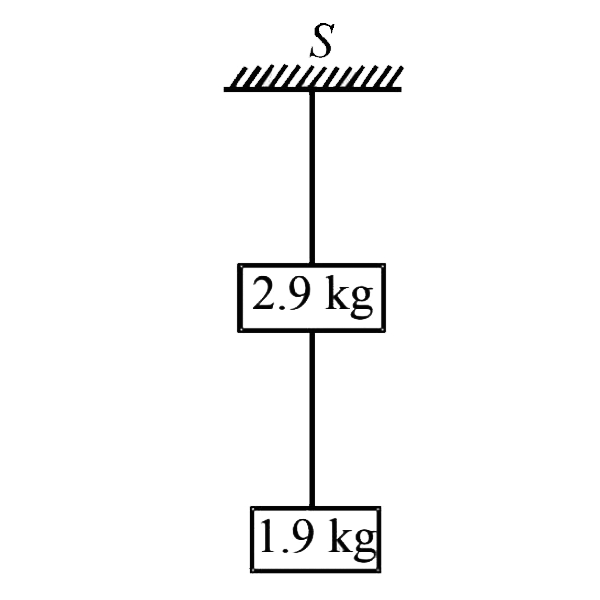
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length `3R//4` is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of `60^@` with the vertical. The spring constant `K=mg//R`. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

View SolutionA particle of mass `10^-2kg` is moving along the positive x axis under the influence of a force `F(x)=-K//(2x^2)` where `K=10^-2Nm^2`. At time `t=0` it is at `x=1.0m` and its velocity is `v=0`.
(a) Find its velocity when it reaches `x=0.50m`.
(b) Find the time at which it reaches `x=0.25m`.
View SolutionIn the figure , masses `m_(1) , m_(2)` and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between `m_(1)` and M and that between `m_(2)` and ground is`0.4` . The pulleys and the string are massless . The string is perfectly horizontal between `P_(1)` and `m_(1)` and also between `P_(2)` and `m_(2)` . The string is perfectly vertical between `P_(1)` and `P_(2)` . An external horizonal force F is applied to the mass M . (Take g = `10 m //s^(2))`
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between `m_(1)` and M be `f_(1)` and that between `m_(2)` and ground be `f_(2)` . For a particular F it is found that `f_(1) = 2f_(2)` . Find `f_(1)` and `f_(2)` . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionTwo block A and B of equal masses are placed on rough inclined plane as shown in figure. When and where will the two blocks come on the same line on the inclined plane if they are released simultaneously? Initially the block A is `sqrt2` m behind the block B. Co-efficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively `(g=10m//s^2)`.
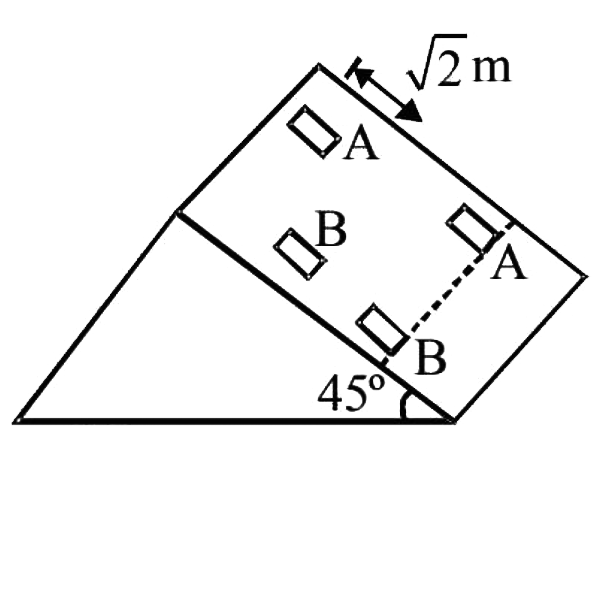
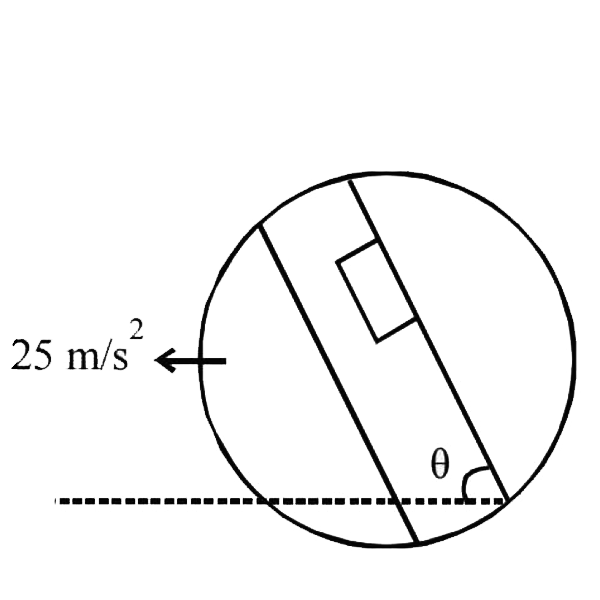
View SolutionA circular disc with a groove along its diameter is placed horizontally on a rough surface. A block of mass 1 kg is placed as shown. The co-efficient of friction between the block and all surfaces of groove and horizontal surface in contact is `mu=2/5`. The disc has an acceleration of `25m//s^2` towards left. Find the acceleration of the block with respect to disc. Given `cos theta=4/5`, `sin theta=3/5`.
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity `omega` is an example of non=inertial frame of reference. The relationship between the force `vecF_(rot)` experienced by a particle of mass m moving on the rotating disc and the force `vecF_(in)` experienced by the particle in an inertial frame of reference is
`vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega`.
where `vecv_(rot)` is the velocity of the particle in the rotating frame of reference and `vecr` is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed `omega` about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis `(vecomega=omegahatk)`. A small block of mass m is gently placed in the slot at `vecr(R//2)hati` at `t=0` and is constrained to move only along the slot.
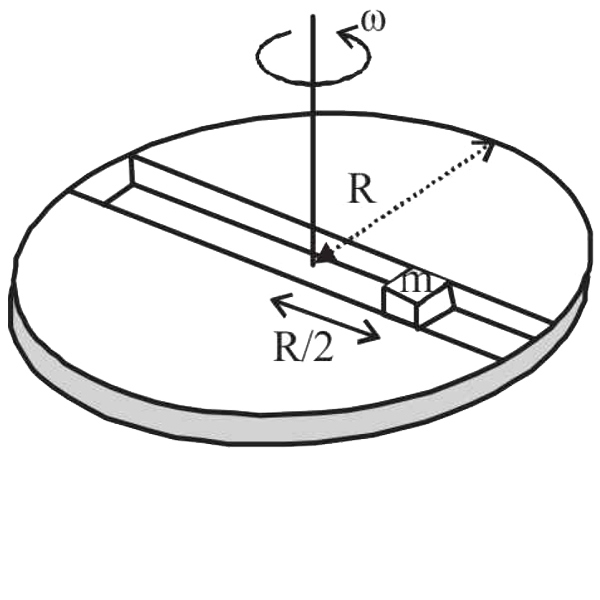
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity `omega` is an example of non=inertial frame of reference. The relationship between the force `vecF_(rot)` experienced by a particle of mass m moving on the rotating disc and the force `vecF_(in)` experienced by the particle in an inertial frame of reference is
`vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega`.
where `vecv_(rot)` is the velocity of the particle in the rotating frame of reference and `vecr` is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed `omega` about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis `(vecomega=omegahatk)`. A small block of mass m is gently placed in the slot at `vecr(R//2)hati` at `t=0` and is constrained to move only along the slot.
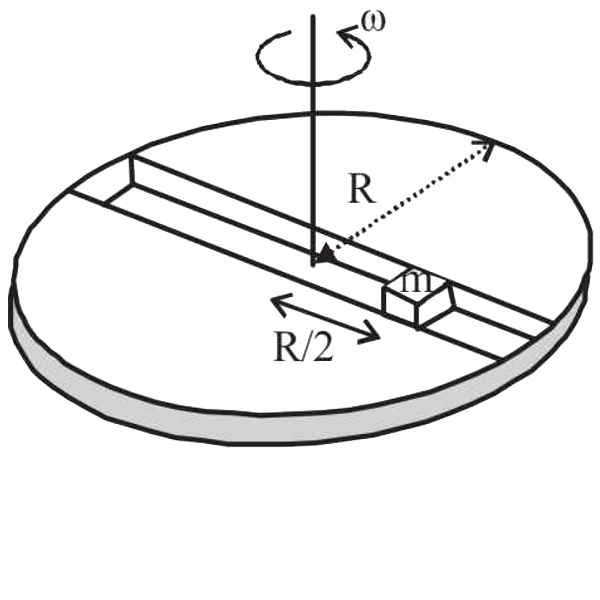
The net reaction of the disc on the block is
View SolutionSTATEMENT-1: A cloth covers a table. Some dishes are kept on it. The cloth can be pulled out without dislodging the dishes from the table.
STATEMENT-2: For every action there is an equal and opposite reaction.
View SolutionSTATEMENT-1: It is easier to pull a heavy object than to push it on a level ground and
STATEMENT-2: The magnitude of frictional force depends on the nature of the two surfaces in contact.
View SolutionA block is moving on an inclined plane making an angle `45^@` with the horizontal and the coefficient of friction is `mu`. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define `N=10mu`, then N is
View SolutionIf a body looses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
View SolutionWhen forces `F_1`, `F_2`, `F_3`, are acting on a particle of mass m such that `F_2` and `F_3` are mutually perpendicular, then the particle remains stationary. If the force `F_1` is now removed then the acceleration of the particle is
View SolutionTwo forces are such that the sum of their magnitudes is 18N and their resultant is 12 N which is perpendicular to the smaller force. Then the magnitude of the forces are
View SolutionSpeeds of two identical cars are u and 4u at at specific instant. The ratio of the respective distances in which the two cars are stopped from that instant is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses `m_1` and `m_2` (vertically). If the acceleration of the system is `g//8`, then the ratio of the masses is
View SolutionThree identical blocks of masses `m=2kg` are drawn by a force `F=10.2N` with an acceleration of `0.6ms^-2` on a frictionless surface, then what is the tension (in N) in the string between the blocks B and C?

View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum tension that the rope can bear is 360 N. With what value of maximum safe acceleration (in `ms^-2`) can a man of 60kg climb down the rope?

View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of `5m//2^2`, the reading of the spring balance will be
View SolutionThree forces start acting simultaneously on a particle moving with velocity, `barv`. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
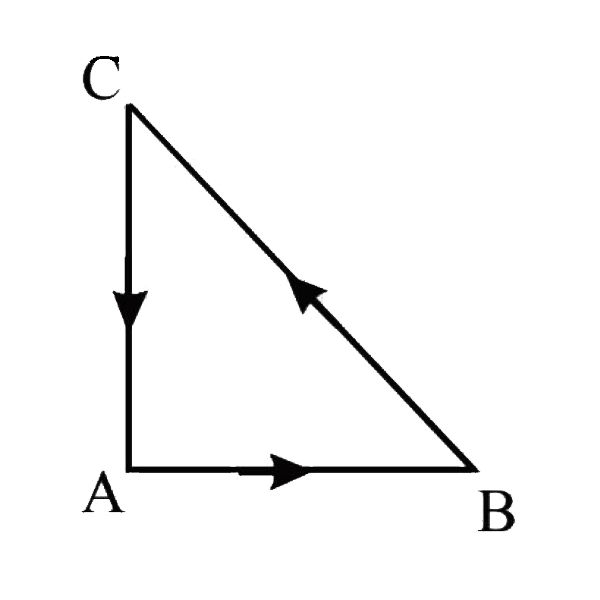
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
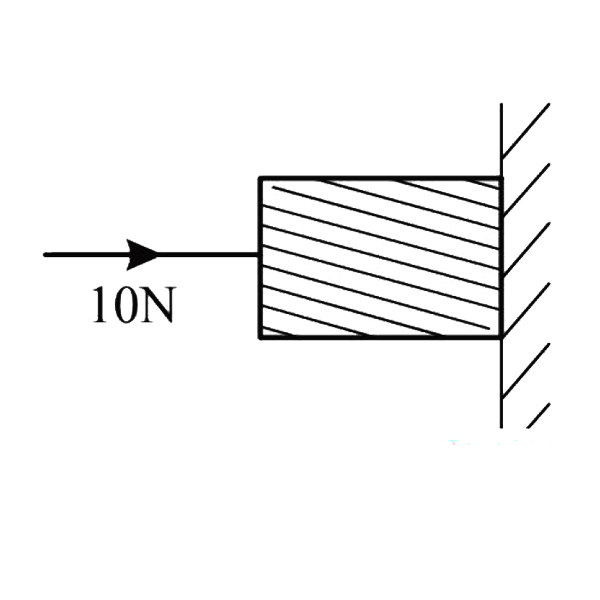
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of `6m//s` is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View SolutionA light spring balance hangs from the hook of the other light spring balance and a block of mass M kg hangs from the former one. Then the true statement about the scale reading is
View SolutionA rocket with a lift-off mass `3.5xx10^4 kg` is blasted upwards with an initial acceleration of `10m//s^2`. Then the initial thrust of the blast is
View SolutionTwo masses `m_1=5kg` and `m_2=4.8kg` tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
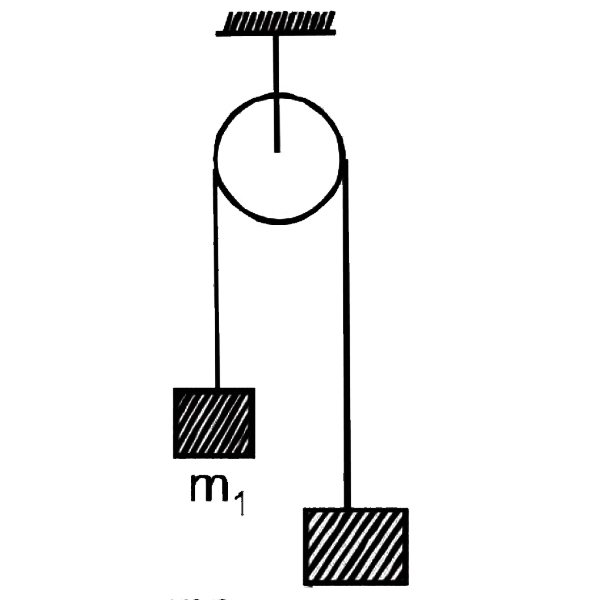
View SolutionA block rests on a rough inclined plane making an angle of `30^@` with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA smooth block is released at rest on a `45^@` incline and then slides a distance 'd'. The time taken to slide is 'n' times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
View SolutionA parachutist after bailing out falls 50m without friction. When parachute opens, it decelerates at `2m//s^2`. He reaches the ground with a speed of `3m//s`. At what height, did the bail out?
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
View SolutionAn annular ring with inner and outer radii `R_1` and `R_2` is rolling wihtout slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, `F_1/F_2` is
View SolutionThe upper half of an inclined plane with inclination `phi` is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionA particle of mass 0.3 kg subject to a force `F=-kx` with `k=15N//m`. What will be its initial acceleration if it is released from a point 20cm away from the origin?
View SolutionA block is kept on a frictionless inclined surface with angle of inclination `alpha`. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to
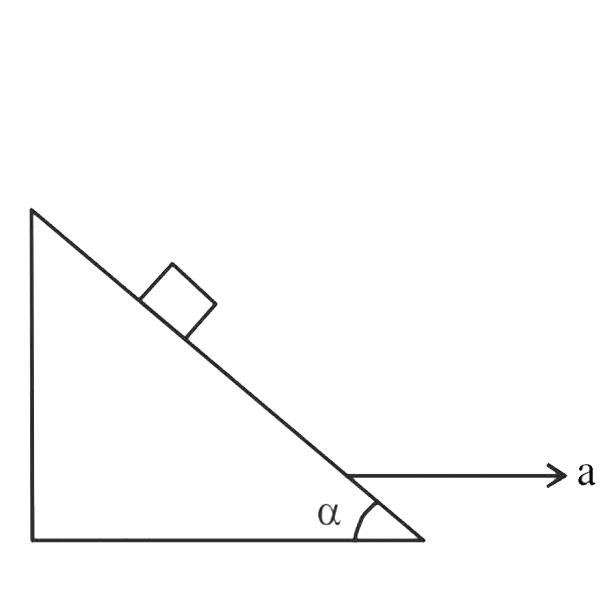
View SolutionConsider a car moving on a straight road with a speed of `100m//s`. The distance at which car can be stopped is `[mu_k=0.5]`
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of `45^@` with the initial vertical direction is
View SolutionA ball of mass 0.2 kg is thrown vertically upwards by applying a force by hand. If the hand moves 0.2 m while applying the force and the ball goes upto 2 m height further, find the magnitude of the force. (Consider `g=10m//s^2`).
View SolutionA player caught a cricket ball of mass 150g moving at a rate of `20m//s`. If the catching process is completed in 0.1s, the force of the blow exerted by the ball on the hand of the player is equal to
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency `omega`. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionTwo fixed frictionless inclined plane making angles `30^(@)` and `60^(@)` with the vertical are shown in the figure. Two blocks A and B are placed on the two planes What is the relative vertical acceleration of A with respect to B ?

View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
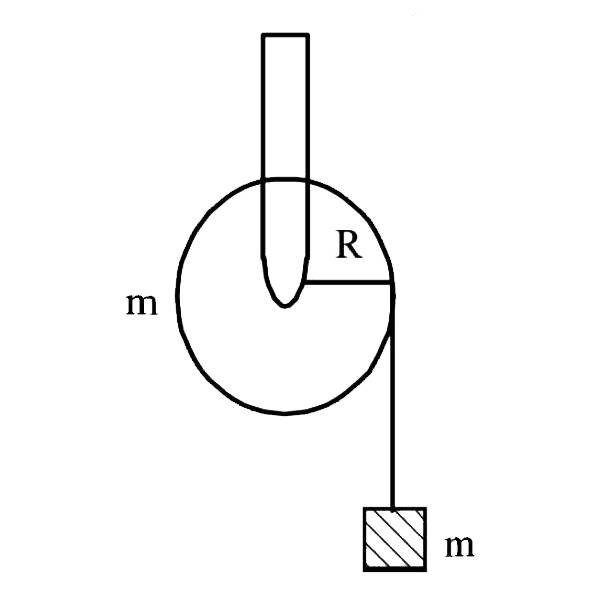
View SolutionA block of mass is placed on a surface with a vertical cross section given by `y=x^3/6`. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals `mu`. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction `mu` and the distance x `(=QR)`, are, respectively close to:

View Solution
JEE Main And Advanced questions and complete solutions for chapter LAWS OF MOTION of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11